MATLAB实现DSB调制与解调
- 格式:doc
- 大小:284.50 KB
- 文档页数:5

课程设计任务书学生姓名: 殷 翔 专业班级: 通信0806 指导教师: 郭志强 工作单位: 信息工程学院 题 目:基于MATLAB 的信号调制与解调 初始条件:(1)MATLAB 软件(2)数字信号处理与图像处理基础知识要求完成的主要任务:(1)已知某消息信号⎪⎩⎪⎨⎧≤≤-≤≤=elset t t t t t m 03/23/23/01)(000以双边幅度调制(DSB-AM )方式调制载波)2cos()(t f t c c π=,所得到的已调制信号记为)(t u ,设s t 15.00=,Hz f c 250=。
试比较消息信号与已调信号,并绘制它们的频谱。
(2)对(1)的DSB-AM 调制信号进行相干解调,并绘出信号的时频域曲线。
(3)对(1)中的信号进行单边带幅度调制(SSB-AM )绘制信号的时频域曲线。
(4)对(1)中的信号进行常规幅度调制(AM ),给定调制指数8.0=a 绘制信号的时频域曲线。
时间安排:第12周:安排任务,分组 第13-14周:设计仿真,撰写报告 第15周:完成设计,提交报告,答辩指导教师签名: 年 月 日系主任(或责任教师)签名:年月日目录摘要 (I)Abstract (II)1.常规双边带幅度调制(DSB-AM)与解调 (1)1.1DSB-AM调制原理与分析 (1)1.2 常规双边带解调原理 (3)2单边带幅度调制(SSB-AM)原理 (5)3常规幅度调制(AM)原理 (6)3.1幅度调制的一般模型 (6)3.2 常规双边带调幅(AM) (7)3.2.1 AM信号的表达式、频谱及带宽 (7)3.2.2 AM信号的功率分配及调制效率 (9)4. 双边幅度调制(DSB-AM)与解调的MATLAB实现 (10)4.1 DSB-AM调制的MATLAB实现 (10)4.2 相干解调 (12)5单边带幅度调制(SSB-AM)的MATLAB实现 (14)6 常规幅度调制(AM)的MATLAB实现 (16)7 小结与收获 (17)8 参考文献 (18)摘要MATLAB是集数值计算,符号运算及图形处理等强大功能于一体的科学计算语言。

利用MATLAB 仿真AM/DSB 调制解调系统一、 系统概述利用MATLAB 的GUI 设计一个仿真AM/DSB 调制解调的系统。
输入不同的参数,产生不同的载波信号、调制信号、调幅信号、解调后信号、滤波后信号。
其中,调幅有标准调幅(AM )和双边带调幅(DSB )两种方案,而滤波器也有FIR 低通滤波和IIR 低通滤波两种选择。
二、背景知识1.振幅调制所谓调制,就是在传送信号的一方将所要传送的信号附加在高频振荡上,再由天线发射出去。
这里高频振荡波就是携带信号的运载工具,也叫载波。
振幅调制,就是由调制信号去控制高频载波的振幅,直至随调制信号做线性变化。
在线性调制系列中,最先应用的一种幅度调制是全调幅或常规调幅,简称为调幅(AM )。
为了提高传输的效率,还有载波受到抑制的双边带调幅波(DSB )和单边带调幅波(SSB )。
本系统采用AM 与DSB 两种调制方式。
设正弦载波为)cos()(0ϕω+=t A t c c式中,A 为载波幅度;c ω为载波角频率;0ϕ为载波初始相位(通常假设0ϕ=0). 调制信号(基带信号)为)(t m 。
根据调制的定义,振幅调制信号(已调信号)一般可以表示为)cos()()(t t Am t s c m ω=设调制信号)(t m 的频谱为)(ωM ,则已调信号)(t s m 的频谱)(ωm S : )]()([2)(c c m M M A S ωωωωω-++= 3.信号解调从高频已调信号中恢复出调制信号的过程称为解调。
对于振幅调制信号,解调就是从它的幅度变化上提取调制信号的过程。
解调是调制的逆过程。
可利用乘积型同步检波器实现振幅的解调,让已调信号与本地恢复载波信号相乘并通过低通滤波可获得解调信号。
4.滤波器解调后的信号还需要进行低通滤波滤去高频部分才能获得所需信号。
低通滤波器种类繁多,每一种原理各不相同。
本系统有FIR 与IIR 两种滤波器可供选择。
三、系统界面简介如图所示,输入参数,选择调幅方案与滤波器后,点击不同的信号按钮,就会在两个坐标系里分别出现该信号的时域波形图和频域波形图。

DSB调制与解调1 课程设计目的本课程设计是实现DSB的调制解调。
在此次课程设计中,我将通过多方搜集资料与分析,来理解DSB调制解调的具体过程和它在MATLAB中的实现方法。
预期通过这个阶段的研习,更清晰地认识DSB的调制解调原理,同时加深对MATLAB 这款通信仿真软件操作的熟练度,并在使用中去感受MATLAB的应用方式与特色。
利用自主的设计过程来锻炼自己独立思考,分析和解决问题的能力,为我今后的自主学习研究提供具有实用性的经验。
2 课程设计要求(1)熟悉MATLAB中M文件的使用方法,掌握DSB信号的调制解调原理,以此为基础用M文件编程实现DSB信号的调制解调。
(2)绘制出SSB信号调制解调前后在时域和频域中的波形,观察两者在解调前后的变化,通过对分析结果来加强对DSB信号调制解调原理的理解。
(3)对信号分别叠加大小不同的噪声后再进行解调,绘制出解调前后信号的时域和频域波形,比较未叠加噪声时和分别叠加大小噪声时解调信号的波形有何区别,由所得结果来分析噪声对信号解调造成的影响。
(4)在老师的指导下,独立完成课程设计的全部内容,并按要求编写课程设计论文,文中能正确阐述和分析设计和实验结果。
3 相关知识在AM 信号中,载波分量并不携带信息,信息完全由边带传送。
如果将载波抑制,只需在将直流0A 去掉,即可输出抑制载波双边带信号,简称双边带信号(DSB )。
DSB 调制器模型如图1所示。
图1 DSB 调制器模型其中,设正弦载波为0()cos()c c t A t ωϕ=+式中,A 为载波幅度;c ω为载波角频率;0ϕ为初始相位(假定0ϕ为0)。
调制过程是一个频谱搬移的过程,它是将低频信号的频谱搬移到载频位置。
而解调是将位于载频的信号频谱再搬回来,并且不失真地恢复出原始基带信号。
双边带解调通常采用相干解调的方式,它使用一个同步解调器,即由相乘器和低通滤波器组成。
在解调过程中,输入信号和噪声可以分别单独解调。

基于Matlab的模拟调制与解调(开放实验)一、实验目的(一)了解AM、DSB和SSB 三种模拟调制与解调的基本原理(二)掌握使用Matlab进行AM调制解调的方法1、学会运用MATLAB对基带信号进行AM调制2、学会运用MATLAB对AM调制信号进行相干解调3、学会运用MATLAB对AM调制信号进行非相干解调(包络检波)(三)掌握使用Matlab进行DSB调制解调的方法1、学会运用MATLAB对基带信号进行DSB调制2、学会运用MATLAB对DSB调制信号进行相干解调(四)掌握使用Matlab进行SSB调制解调的方法1、学会运用MATLAB对基带信号进行上边带和下边带调制2、学会运用MATLAB对SSB调制信号进行相干解调二、实验环境MatlabR2020a三、实验原理(一)滤波法幅度调制(线性调制)(二)常规调幅(AM)1、AM表达式2、AM波形和频谱3、调幅系数m(三)抑制载波双边带调制(DSB-SC)1、DSB表达式2、DSB波形和频谱(四)单边带调制(SSB)(五)相关解调与包络检波四、实验过程(一)熟悉相关内容原理 (二)完成作业已知基带信号()()()sin 10sin 30m t t t ππ=+,载波为()()cos 2000c t t π= 1、对该基带信号进行AM 调制解调(1)写出AM 信号表达式,编写Matlab 代码实现对基带进行进行AM 调制,并分别作出3种调幅系数(1,1,1m m m >=<)下的AM 信号的时域波形和幅度频谱图。
代码 基带信号fs = 10000; % 采样频率 Ts = 1/fs; % 采样时间间隔t = 0:Ts:1-Ts; % 时间向量m = sin(10*pi*t) + sin(30*pi*t); % 基带信号载波信号fc = 1000; % 载波频率c = cos(2*pi*fc*t); % 载波信号AM调制Ka = [1, 0.5, 2]; % 调制系数m_AM = zeros(length(Ka), length(t)); % 存储AM调制信号相干解调信号r = zeros(length(Ka), length(t));绘制AM调制信号的时域波形和幅度频谱图figure;for i = 1:length(Ka)m_AM(i, :) = (1 + Ka(i)*m).*c; % AM调制信号subplot(3, 2, i);plot(t, m_AM(i, :));title(['AM调制信号(Ka = ' num2str(Ka(i)) ')']);xlabel('时间');ylabel('幅度');ylim([-2, 2]);subplot(3, 2, i+3);f = (-fs/2):fs/length(m_AM(i, :)):(fs/2)-fs/length(m_AM(i, :));M_AM = fftshift(abs(fft(m_AM(i, :))));plot(f, M_AM);title(['AM调制信号的幅度频谱图(Ka = ' num2str(Ka(i)) ')']);xlabel('频率');ylabel('幅度');r(i, :) = m_AM(i, :) .* c; % 相干解调信号end绘制相干解调信号的时域波形和幅度频谱图figure;for i = 1:length(Ka)subplot(length(Ka), 1, i);plot(t, r(i, :));title(['相干解调信号(Ka = ' num2str(Ka(i)) ')']);xlabel('时间');ylabel('幅度');end图像(2)编写Matlab代码实现对AM调制信号的相干解调,并作出图形。

实验3:DSB 调制与解调仿真一、实验目的1.掌握DSB 的调制原理和Matlab Simulink 仿真方法2.掌握DSB 的解调原理和Matlab Simulink 仿真方法二、实验原理1. DSB 信号的调制解调原理:1.1 调制原理:在幅度调制的一般模型中,若假设滤波器为全通网络(H(w)=1),调制信号中无直流分量,则输出的已调信号就是无载波分量的双边带调制信号(DSB)。
每当信源信号极性发生变化时,调制信号的相位都会发生一次突变π。
SDSB(t)=m(t)coswCt 调制的目的就是进行频谱搬移,把调制信号的频谱搬移到所希望的位置上,从而提高系统信息传输的有效性和可靠性。
DSB调制原理框图如下图1.2 解调原理:DSB只能进行想干解调,其原理框图与AM信号相干解调时完全相同,利用恢复的载波与信号相乘,将频谱搬移到基带,还原出原基带信号,DSB解调原理框图如下图三、实验步骤1、DSB模拟系统调制方式的MATLAB Simulink仿真(1)原理图(2)仿真图(3)仿真分析①调制器②调制后信号对比调制前的信号,周期变小,频率变大了,幅度随时间在不断的呈现周期性变化,在0~0.6之间,小于调制前的幅度。
2、DSB解调方式的MATLAB Simulink仿真(1)原理图(2)仿真图(3)仿真分析①调制器②解调后周期变大,频率变小,幅度会有所减小,在0 ~0.25之间。
3、用示波器观察DSB调制解调输入和输出信号波形(1)原理图(2)仿真图(3)仿真分析解调后周期不变,频率也不会改变,幅度会有所减小,在0 ~0.25之间。
4、Zero-Order Hold和Spectrum Scope观察DSB调制仿真前后的频谱图(1)原理图(2)仿真图输入信号源的频谱图解调器输出信号的频谱图(3)仿真分析在频谱结构上,它的频谱完全是基带信号频谱在频域内的简单搬移,若调制信号频率为w,载波频率wc,调制后信号频率搬移至处w-wc和w+wc;经解调和滤波后又回到原位。

通信原理课程设计题目:基于MATLAB的抑制载波的双边带幅度调制(DSB)与解调分析——解调分析学院计算机与通信工程学院专业通信工程学号 20130000姓名 XXX指导老师童峥嵘宫铭举2015年12月通信原理课程设计评分标准摘要信号的调制与解调在通信系统中具有重要的作用。
调制过程实际上是一个频谱搬移的过程,即是将低频信号的频谱(调制信号)搬移到载频位置(载波)。
而解调是调制的逆过程,即是将已调制信号还原成原始基带信号的过程。
调制与解调方式往往能够决定一个通信系统的性能。
幅度调制就是一种很常见的模拟调制方法,在AM信号中,载波分量并不携带信息,仍占据大部分功率,如果抑制载波分量的发送,就能够提高功率效率,这就抑制载波双边带调制DSB-SC(Double Side Band with Suppressed Carrier),因为不存在载波分量,DSB-SC信号的调制效率就是100%,即全部功率都用于信息传输。
但由于DSB-SC信号的包络不再与调制信号的变化规律一致,因而不能采用简单的包络检波来恢复调制信号,需采用同步检波来解调。
这种解调方式被广泛应用在载波通信和短波无线电话通信中。
但是由于在信道传输过程中必将引入高斯白噪声,虽然经过带通滤波器后会使其转化为窄带噪声,但它依然会对解调信号造成影响,使其有一定程度的失真,而这种失真是不可避免的。
本文介绍了M文件编程方法来仿真DSB-SC系统的整个解调过程。
关键词 DSB-SC调制同步检波信道噪声 M语言目录第一章绪论 11.1 引言 11.2 信号的处理 11.3 本章小结 2第二章 DSB-SC的基本原理 32.1 DSB-SC解调原理 32.1.1 DSB-SC的解调原理分析 3 2.1.2 DSB-SC的解调框图 3 2.2 DSB-SC系统框图 42.3 本章小结 4第三章 Matlab介绍 53.1 Matlab简介 53.2 m语言的特点及构成 53.3 本章小结 6第四章m语言的模块与仿真图 7 4.1 高斯白噪声 74.1.1.高斯白噪声下的信道特征 84.1.2.噪声仿真程序及仿真图 84.2 解调部分程序及仿真图 84.3 带通滤波器 94.4 本章小结 9第五章 M文件完整程序 11第六章总结 17参考文献 17第1章绪论1.1 引言通信的首要目的是传输信息,如何准确高效地传输信息是通信的一个重要目标。

信号与系统课程设计报告书课题名称 MATLAB 实现DSB 的调制与解调 姓 名学 号 院、系、部 电气系 专 业 电子信息工程指导教师20年 月日※※※※※※※※※ ※※ ※※ ※※ ※※※※※※※※※200级信号与系统 课程设计目录一、设计目的:......................................................................................................... 3二、设计要求:......................................................................................................... 3三、设计原理: (3)四、程序设计 ............................................................................................................ 4五、仿真结果:......................................................................... 错误!未定义书签。
六、设计总结 ............................................................................................................ 5七、参考文献 ............................................................................................................ 6MATLAB实现DSB的调制与解调一、设计目的熟练掌握MATLAB语言,实现调幅双边带的调制与解调,巩固已经学过的知识,加深对知识的理解和应用,加强学科间的横向联系,学会应用MATLAB对离散系统进行仿真。

目录前言 (2)1 DSB调制与解调原理 (3)1.1DSB调制原理 (3)1.2DSB解调原理与抗噪性能 (5)2 DSB调制解调分析的MATLAB实现 (7)2.1正弦波调制 (7)2.1.1调制信号幅度=0.8×载波幅度 (7)2.1.2调制信号幅度=载波幅度 (9)2.1.3调制信号幅度=1.5*载波幅度 (11)2.2矩形波调制 (12)2.2.1调制信号幅度=0.8×载波幅度 (12)2.2.2调制信号幅度=载波幅度 (14)2.2.3调制信号幅度=1.5*载波幅度 (15)3结论 (17)4参考文献 (18)5附录 (19)前言调制在通信系统中有十分重要的作用。
通过调制,不仅可以进行频谱搬移,把调制信号的频谱搬移到所希望的位置上,从而将调制信号转换成适合于传播的已调信号,而且它对系统的传输有效性和传输的可靠性有着很大的影响,调制方式往往决定了一个通信系统的性能。
MATLAB软件广泛用于数字信号分析,系统识别,时序分析与建模,神经网络、动态仿真等方面有着广泛的应用。
本课题利用MATLAB软件对DSB调制解调系统进行模拟仿真,分别利用300HZ正弦波和矩形波,对30KHZ正弦波进行调制,观察调制信号、已调信号和解调信号的波形和频谱分布,并在解调时引入高斯白噪声,对解调前后信号进行信噪比的对比分析,估计DSB调制解调系统的性能。
第1章DSB调制与解调原理1.1 DSB调制原理DSB调制属于幅度调制。
幅度调制是用调制信号去控制高频载波的振幅,使其按调制信号的规律而变化的过程。
设正弦型载波c(t)=Acos(ωc t),式中:A为载波幅度,ωc为载波角频率。
根据调制定义,幅度调制信号(已调信号)一般可表示为:Sm(t)=Am(t)cos(ωc t)(1-1),其中,m(t)为基带调制信号。
设调制信号m(t)的频谱为M(ω),则由公式1-1不难得到已调信号Sm(t)的频谱Sm(ω)=A[M(ωc+ω)+M(ωc+ω)]/2(1-2)由以上表示式可见,在波形上,幅度已调信号随基带信号的规律呈正比地变化;在频谱结构上,它的频谱完全是基带信号频谱在频域内的简单搬移。

抑制载波双边带幅度调制、相干解调系统的MATLAB实现目录一、作业要求 (1)二、DSB-SC原理描述 (1)三、DSB-SC实现框图 (2)四、MATLAB程序及注释 (3)五、仿真结果 (11)一、作业要求用MATLAB程序开发设计抑制载波双边带幅度调制、相干解调系统。
系统参数如下:信源为频率为3K、幅度为1的正弦信号,载波频率为信源频率的30倍。
要求有如下输出和显示:(1)调制前后的信号波形、信号频谱;(2)在信道输入信噪比分别为0dB和10dB两种情况下,解调器的输入和输出波形各有何不同;(3)绘出输入信噪比与输出信噪比之间的关系(不能直接使用制度增益的公式来绘制)。
二、DSB-SC原理描述所谓线性调制是指信号的频谱为调制信号(即基带信号)频谱的线性平移及变换,而非线性调制时已调信号与输入调制信号之间不存在这种对应关系,已调信号频谱中将出现与调制信号无线性关系的分量。
在常规双边带调幅(DSB )时,由于已调波中含有不携带信息的载波分量,故调制效率较低。
为了提高调制效率,在常规调幅的基础上抑制掉载波分量,使总功率全部包含在双边带中。
这种调制方式称为抑制载波双边带调制 (DSB-SC)。
在抑制载波双边带调幅(DSB-SC )中,实现双边带调制就是完成调制信号与载波信号的相乘运算,输出已调信号时域表达式为:()()()=DSB c S t f t cos w t其中f(t)为调制信号,可确切知道也可以为随机信号,通常认为平均值为0。
ωc 为载波频率。
双边带解调只能采用相干解调,把已调信号乘上一个与调制器同频同相的载波,将已调信号的频谱搬回到原点位置,时域表达式为:21()()()()(12)2==+DSB c c c S t cos w t f t cos w t f t cos w t 然后通过低通滤波器,滤除高频分量,使得无失真地恢复出原始调制信号。
三、DSB-SC 实现框图DSB_SC 信号的产生:f(t)cos(wt)S(t)DSB_SC信号的解调:四、MATLAB程序及注释clc;clear;tic;fm=3*10^3;%pre modulation freqfc=30*fm;%carrier freqfs=2*2^10*fc;%sampling freqT=1/fs;%sampling intervalL=256*2^10;%length of signalt=(0:L-1)*T;%time vectorft=sin(2*pi*fm*t);%pre-modulation signalplot(t,ft);title('premodulation signal');xlabel('t/s');ylabel('f(t)');saveas(gcf,'premodulation signal.bmp','bmp');s_dsb=ft.*cos(2*pi*fc*t);%modulated signalplot(t,s_dsb);title('modulated signal');xlabel('t/s');ylabel('dsb(t)');saveas(gcf,'modulated signal.bmp','bmp');NFFT=2^nextpow2(L);fw_ft=fft(ft,NFFT)/NFFT*2;%show reality ampltitudef=fs/NFFT*(0:1:NFFT-1);abs_fw_ft=abs(fw_ft);plot(f(1:NFFT/2),abs_fw_ft(1:NFFT/2));saveas(gcf,'premodulation signal spectrum.bmp','bmp');plot(f(1:ceil(10*fm*L*T)),abs_fw_ft(1:ceil(10*fm*L*T)));%better effectfw_dsb=fft(s_dsb,NFFT)/NFFT*2;abs_fw_dsb=abs(fw_dsb);plot(f(1:NFFT/2),abs_fw_dsb(1:NFFT/2));saveas(gcf,'modulated signal spectrum.bmp','bmp');plot(f(1:ceil(2*fc*L*T)),abs_fw_dsb(1:ceil(2*fc*L*T)));%better effect%--------------------------------------q2dsb_n0=awgn(s_dsb,0);%add noiseplot(t,dsb_n0);dsb_n10=awgn(s_dsb,10);plot(t,dsb_n10);fw_dsb_n0=fft(dsb_n0,NFFT);%fftabs_fw_dsb_n0=abs(fw_dsb_n0);plot(f(1:NFFT/2),abs_fw_dsb_n0(1:NFFT/2));fw_dsb_n10=fft(dsb_n10,NFFT);abs_fw_dsb_n10=abs(fw_dsb_n10);plot(f(1:NFFT/2),abs_fw_dsb_n10(1:NFFT/2));[max_n0,locat_n0]=max(abs_fw_dsb_n0(1:NFFT/2));%bpf_n0w_bpf=11;%适当的取带通滤波器的带宽,会影响最后的制度增益abs_fw_dsb_n0(:,1:(locat_n0-w_bpf))=0;abs_fw_dsb_n0(:,(locat_n0+w_bpf):NFFT-locat_n0-w_bpf)=0;abs_fw_dsb_n0(:,NFFT-locat_n0+w_bpf:NFFT)=0;fw_dsb_n0(:,1:(locat_n0-w_bpf))=0;fw_dsb_n0(:,(locat_n0+w_bpf):NFFT-locat_n0-w_bpf)=0;fw_dsb_n0(:,NFFT-locat_n0+w_bpf:NFFT)=0;[max_n10,locat_n10]=max(abs_fw_dsb_n10(1:NFFT/2));%bpf_n10 %w_bpf=5;abs_fw_dsb_n10(:,1:(locat_n10-w_bpf))=0;abs_fw_dsb_n10(:,(locat_n10+w_bpf):NFFT-locat_n10-w_bpf)=0; abs_fw_dsb_n10(:,NFFT-locat_n10+w_bpf:NFFT)=0;fw_dsb_n10(:,1:(locat_n10-w_bpf))=0;fw_dsb_n10(:,(locat_n10+w_bpf):NFFT-locat_n10-w_bpf)=0;fw_dsb_n10(:,NFFT-locat_n10+w_bpf:NFFT)=0;% tic;%bpf1 %slow time wasting,no loop% for i=1:size(fw_dsb_n0,2)% max_abs_fw_n0=max(abs_fw_dsb_n0);% if abs_fw_dsb_n0(i)<0.1*max_abs_fw_n0% fw_dsb_n0(i)=0;% abs_fw_dsb_n0(i)=0;% end% end% toc;% tic;%bpf2% for i=1:size(fw_dsb_n10,2)% max_abs_fw_n10=max(abs_fw_dsb_n10);% if abs_fw_dsb_n10(i)<0.1*max_abs_fw_n10% fw_dsb_n10(i)=0;% abs_fw_dsb_n10(i)=0;% end% end% toc;fti_n0=ifft(fw_dsb_n0);%input signalfti_n10=ifft(fw_dsb_n10);fti_n0=real(fti_n0);fti_n10=real(fti_n10);plot(t,fti_n0);plot(t,fti_n10);dsb_n0_temp=fti_n0.*cos(2*pi*fc*t);fw_dsbi_n0=fft(dsb_n0_temp,NFFT);fw_dsbi_n0(:,ceil((1.5*fm)*L*T):NFFT-ceil((1.5*fm)*L*T))=0;%lpf %适当的取低通滤波器的带宽,会影响最后的制度增益abs_fw_dsbi_n0=abs(fw_dsbi_n0);plot(f(1:NFFT/2),abs_fw_dsbi_n0(1:NFFT/2));fto_n0=ifft(fw_dsbi_n0);%output signalfto_n0=real(fto_n0);plot(t,fto_n0);dsb_n10_temp=fti_n10.*cos(2*pi*fc*t);fw_dsbi_n10=fft(dsb_n10_temp,NFFT);fw_dsbi_n10(:,ceil((1.5*fm)*L*T):NFFT-ceil((1.5*fm)*L*T))=0;%lpf abs_fw_dsbi_n10=abs(fw_dsbi_n10);plot(f(1:NFFT/2),abs_fw_dsbi_n10(1:NFFT/2));fto_n10=ifft(fw_dsbi_n10);%output signalfto_n10=real(fto_n10);plot(t,fto_n10);plot(t,fto_n10-fto_n0);%difference btw n10&n0%------------------------------------q3sini=zeros(1,201);sono=zeros(1,201);for snr=0:200dsb_n_snr=awgn(s_dsb,snr);%add noiseplot(t,dsb_n_snr);fw_dsb_n_snr=fft(dsb_n_snr,NFFT);%fftabs_fw_dsb_n_snr=abs(fw_dsb_n_snr);plot(f(1:NFFT/2),abs_fw_dsb_n_snr(1:NFFT/2));[max_n_snr,locat_n_snr]=max(abs_fw_dsb_n_snr(1:NFFT/2));%bpf_n _snr%w_bpf=5;abs_fw_dsb_n_snr(:,1:(locat_n_snr-w_bpf))=0;abs_fw_dsb_n_snr(:,(locat_n_snr+w_bpf):NFFT-locat_n_snr-w_bpf)=0; abs_fw_dsb_n_snr(:,NFFT-locat_n_snr+w_bpf:NFFT)=0;fw_dsb_n_snr(:,1:(locat_n_snr-w_bpf))=0;fw_dsb_n_snr(:,(locat_n_snr+w_bpf):NFFT-locat_n_snr-w_bpf)=0;fw_dsb_n_snr(:,NFFT-locat_n_snr+w_bpf:NFFT)=0;fti_n_snr=ifft(fw_dsb_n_snr);%input signalfti_n_snr=real(fti_n_snr);plot(t,fti_n_snr);dsb_n_snr_temp=fti_n_snr.*cos(2*pi*fc*t);fw_dsbi_n_snr=fft(dsb_n_snr_temp,NFFT);fw_dsbi_n_snr(:,ceil((1.5*fm)*L*T):NFFT-ceil((1.5*fm)*L*T))=0;%lpfabs_fw_dsbi_n_snr=abs(fw_dsbi_n_snr);plot(f(1:NFFT/2),abs_fw_dsbi_n_snr(1:NFFT/2));fto_n_snr=ifft(fw_dsbi_n_snr);%output signalfto_n_snr=real(fto_n_snr)*2;%after lpf we acquire ft/2,so we need to *2plot(t,fto_n_snr);sini(1,snr+1)=10*log10(abs(mean(mean(ft(32768:229376).*ft(327 68:229376)))/(mean(mean(fti_n_snr(32768:229376)-ft(32768:229376)).*(fti_n_snr(32768:229376)-ft(32768:229376))))));sono(1,snr+1)=10*log10(abs(mean(mean(ft(32768:229376).*ft(32 768:229376)))/(mean(mean(fto_n_snr(32768:229376)-ft(32768:229376)).*(fto_n_snr(32768:229376)-ft(32768:229376))))));%取不受加窗影响的信号段endsnr_x=0:200;plot(snr_x,sono./sini);toc;% subplot(3,1,1);plot(t(32768:229376),ft(32768:229376));% subplot(3,1,2);plot(t(32768:229376),fti_n_snr(32768:229376)); % subplot(3,1,3);plot(t(32768:229376),fto_n_snr(32768:229376));五、仿真结果在MATLAB仿真中,取系统参数如下:信源为频率为3K、幅度为1的正弦信号,载波频率为信源频率的30倍,即为90K。
MATLAB实现DSB调制与解调MATLAB 实现DSB 调制与解调学⽣:黄⽂伯班级:通信112指导⽼师:⽂欢⼀、研究的主要内容和研究的意义通过本次课设更深⼊的了解DSB 调制和解调的基本原理以及利⽤MATLAB 软件对DSB 信号的调制解调,深⼊地理解调制解调技术在通信⼯程专业系列课程中的理论基础地位、作⽤和意义;加深对基本概念和基本原理的理解,并能够⽤所学知识进⾏调制解调仿真及性能分析。
⼆、DSB 调制与解调原理DSB 是AM 调制的⼀种,AM 信号通过信道后⾃然会叠加有燥声,经过接收天线进⼊带通滤波器。
BPF 的作⽤有两个,⼀是让AM 信号直接通过,⼆是滤出带外噪声。
AM 信号通过BFP 后与本地载波相乘后。
进⼊LPF ,LPF 的截⽌频率设定为⼀个定值,它不允许频率⼤于截⽌频率的成分通过,因此LPF 的输出仅为与要的信号。
三、⾼斯⽩噪声在实际信号传输过程中,通信系统不可避免的会遇到噪声,例如⾃然界中的各种电磁波噪声和设备本⾝产⽣的热噪声、散粒噪声等,它们很难被预测。
⽽且⼤部分噪声为随机的⾼斯⽩噪声,所以在设计时引⼊噪声,才能够真正模拟实际中信号传输所遇到的问题,进⽽思考怎样才能在接受端更好地恢复基带信号。
信道加性噪声主要取决于起伏噪声,⽽起伏噪声⼜可视为⾼斯⽩噪声,因此我在此环节将对双边带信号添加⾼斯⽩噪声来观察噪声对解调的影响情况。
四、模拟仿真结果分析通过MATLAB 对DSB 调制和解调系统的模拟仿真,观察各波形和频谱,在波形上,已调信号的幅度随基带信号的规律呈正⽐地变化;在频谱结构上,它的频谱完全是基带信号频谱在频域内的简单搬移,若调制信号频率为,载波频率,调制后信号频率搬移⾄处。
通过在已调信号中加⼊⾼斯⽩噪声,通过解调器解调,根据对输⼊输出信噪⽐关系曲线绘制观察,在理想情况下,输出信噪⽐为输⼊信噪⽐的⼆倍,即DSB 信号的解调器使信噪⽐改善s m c⼀倍;不同的调制信号对系统性能有⼀定的影响。

目录1基于MATLAB的抑制载波的双边带幅度调制(DSB)与解调分析摘要 (2)2、设计目的 (3)3、设计要求 (4)4、系统原理 (4)4.1系统框图: (4)4.2各模块原理及M文件实现 (5)4.2.1.发送与接收滤波器 (8)4.2.2.解调部分 (8)5 Simulink仿真 (11)5.1:调制仿真 (11)5.2:调制+解调 (15)5.3:调制+高斯噪声+解调 (18)5.4总结: (21)6、M文件完整程序 (22)7、个人小结 (28)8、参考文献 (29)1基于MATLAB的抑制载波的双边带幅度调制(DSB)与解调分析摘要信号的调制与解调在通信系统中具有重要的作用。
调制过程实际上是一个频谱搬移的过程,即是将低频信号的频谱(调制信号)搬移到载频位置(载波)。
而解调是调制的逆过程,即是将已调制信号还原成原始基带信号的过程。
调制与解调方式往往能够决定一个通信系统的性能。
幅度调制就是一种很常见的模拟调制方法,在AM信号中,载波分量并不携带信息,仍占据大部分功率,如果抑制载波分量的发送,就能够提高功率效率,这就抑制载波双边带调制DSB-SC(Double Side Band with Suppressed Carrier),因为不存在载波分量,DSB-SC信号的调制效率就是100%,即全部功率都用于信息传输。
但由于DSB-SC信号的包络不再与调制信号的变化规律一致,因而不能采用简单的包络检波来恢复调制信号,需采用同步检波来解调。
这种解调方式被广泛应用在载波通信和短波无线电话通信中。
但是由于在信道传输过程中必将引入高斯白噪声,虽然经过带通滤波器后会使其转化为窄带噪声,但它依然会对解调信号造成影响,使其有一定程度的失真,而这种失真是不可避免的。
本文介绍了M文件编程和Simulink 两种方法来仿真DSB-SC系统的整个调制与解调过程。
关键词DSB-SC调制同步检波信道噪声M文件Simulink仿真2、设计目的本课程设计是实现模拟DSB-SC信号的调制解调。
前言 (1)工程概况 (1)正文 (1)3.1设计的目的和意义 (1)3.1.1设计的目的 (1)3.1.2设计的意义 (1)3.2 DBS FM与解调原理 (2)3.2.DSB调制的原理 (2)3.2.2抑制载波的双边带调制与解调的原理 (2)3.3 DSB和AM的解调与调制分析 (3)3.3.1 DSB原始信号和已调信号的时域与频域 (3)3.3.2 FM原始信号和已调信号的时域与频域 (6)3.4 结论 (8)致谢 (8)参考文献 (9)在当今高度信息化的社会,信息和通信已成为现代社会的命脉。
信息作为一种资源,只有通过广泛的传播和交流,才能产生利用价值,促进社会成员的合作,推动社会生产力的发展,创造出巨大的经济效益。
而通信作为传输信息的手段或方式,与传感技术,计算机技术相互融合,已成为21世纪国际社会和世界经济发展的强大推动力。
可以预见,未来的通信对人们的生活方式和社会的发展将产生更加重大和意义深远的影响。
信号的调制与解调在通信系统中具有重要的作用。
调制过程是一个频谱搬移的过程,它是将低频信号的频谱搬移到载频位置。
解调是调制的逆过程,即是将已调制的信号还原成原始基带信号的过程。
信号的接收端就是通过解调来还原已调制信号从而读取发送端发送的信息。
因此信号的解调对系统的传输有效性和传输可靠性有着很大的影响。
调制与解调方式往往决定了一个通信系统的性能。
本课程设计主要论述了FM和DSB基本原理以及如何在MATALB环境中实现FM和DSB的调制与解调,在这里使用m(t)=sinc(100*t)作为基带信号进行调制,形式简单,便于产生及接收。
做此课程设计不仅加强了我们对原来的通信原理知识的巩固和了解,更加对利用MATLAB这个工具如何进行通信仿真有了更进一步的了解,为以后用MATLAB做诸如此类的学习与研究打下了基础。
工程概况本次课程设计的主题是采用MATLAB仿真实现FM、DSB的调制与解调。
首先要求对MATLAB 软件有着较为深入地了解和认识,掌握一些MATLAB语言的用法,对MATLAB代码进行仿真,例如:用MATLAB的代码实现电路的正弦波波形图、频谱分析图等等。
AM 、DSB 调制及解调用matlab 产生一个频率为1Hz ,功率为1的余弦信源()m t ,设载波频率10c Hz ω=,02m =,试画出:●AM 及DSB 调制信号的时域波形;● 采用相干解调后的AM 及DSB 信号波形; ● AM 及DSB 已调信号的功率谱;● 调整载波频率及m0,观察分的AM 的过调与DSB 反相点现象。
● 在接收端带通后加上窄带高斯噪声,单边功率谱密度00.1n =,重新解调。
一 图表输出及结果分析1 AM 及DSB 调制信号的时域波形-505AM 调制信号t/s幅度-5-4-3-2-1012345-202DSB 调制信号t/s幅度AM 信号的包络波形与其调制信号的波形完全一样。
DSB 调制信号在载波处反向。
2 采用相干解调后的AM 及DSB 信号波形0.511.522.533.544.55t/sm (t )AM 相干解调t/sm (t )DSB 相干解调AM 信号可用包络检波器检波,滤除直流后可恢复出原信号。
与AM 相比,DSB 信号由于不存在载波分量,全部功率都用来传输信息。
3 AM 及DSB 已调信号的功率谱AM 已调信号功率谱f/hzwDSB 已调信号功率谱f/hzwAM 信号所需的传输带宽为调制信号带宽的两倍。
DSB 节省了载波功率,但所需的传输带宽仍为调制信号带宽的两倍。
4 调整载波频率及m0,观察分的AM 的过调与DSB 反相点现象。
-5-4-3-2-112345AM 不过调t/s 幅度-5-4-3-2-1012345AM 过调t/s幅度DSB 调幅波w/(2*pi)幅度w/(2*pi)相位AM 信号用于包络检波器检波时,当调制信号的最大值大于直流信号时,会出现“过调制”现象,此时会发生失真。
DSB 相位在0.2π角频率处频率处明显存在反相点现象。
5 在接收端带通后加上窄带高斯噪声,单边功率谱密度00.1n ,重新解调。
t/sm (t )AM 相干解调t/sm (t )DSB 相干解调加入相同功率的高斯白噪声信号,DSB 信号解调较AM 信号解调误差较大。
课程设计任务书学生姓名: 专业班级:指导教师: 工作单位:题 目: 基于MATLAB 的信号调制与解调 初始条件:1.Matlab 应用软件;2.信号处理的相关知识,线性代数基础知识,希尔伯特变换;3.信号的常规幅度调制,单边带幅度调制以及双边带调制。
要求完成的主要任务:设计任务1:应用MATLAB 求解基本的高等应用数学问题。
设计任务2:已知某消息信号⎪⎩⎪⎨⎧≤≤-≤≤=elset t t t t t m 03/23/23/01)(000,以双边幅度调制(DSB-AM )方式调制载波)2cos()(t f t c c π=,所得到的已调制信号记为)(t u ,设s t 15.00=,Hz f c 250=。
(1)试比较消息信号与已调信号,并绘制它们的频谱。
(2)对(1)中的DSB-AM 调制信号进行相干解调,并绘出信号的时频域曲线。
(3)对(1)中的信号进行单边带幅度调制(SSB-AM ),绘制信号的时频域曲线。
(4)对(1)中的信号进行常规幅度调制(AM ),给定调制指数8.0=a ,绘制信号的时频域曲线。
设计要求:1.设计的程序有较强的可行性,能够很好地反映出MATLAB 强大的运算功能和工程实用性;掌握MATLAB 在数学和工程上的应用技术,学习实际可用的应用程序的编写;2.撰写出具有较强实用性、应用性的MATLAB 论文。
时间安排:第17周:安排任务,分组,资料准备;第17-18周:设计仿真,撰写报告;第19周:完成设计,提交报告,答辩。
指导教师签名: 年 月 日 系主任(或责任教师)签名: 年 月 日目录摘要 (1)Abstract (2)1绪论 (3)1.1MTLAB软件简介. (3)1.2MATLAB语言的特点和开发环境. (3)2 高等应用数学问题的MATLAB求解. (4)2.1 高等数学常见的函数基本计算 (4)2.2 线性代数常见的矩阵基本计算 (6)2.3 高等数学常见的多项式基本计算 (10)3 基于MATLAB的信号调制与解调 (13)3.1 常规双边带调制与解调及相干解调 (13)3.2 抑制载波的双边带调幅与解调 (16)3.3 单边带调制与解调 (17)3.4 基于MATLAB的信号调制与解调 (19)4 小结与体会 (25)5 主要参考文献 (26)摘要MATLAB 的名称源自 Matrix Laboratory ,它是一种科学计算软件,专门以矩阵的形式处理数据,其含义是矩阵实验室(MATRIX LABORATORY),进行数值计算的基本单位是复数数组(或称阵列),由于它不需定义数组的维数,并给出矩阵函数、特殊矩阵专门的库函数,使之在求解诸如信号处理、建模、系统识别、控制、优化等领域的问题时,显得大为简捷、高效、方便。
目录1 DSB调制的根本原理 (1)2 DSB调制与解调的MATLAB实现 (3) (3) (4) (6) (7)3 simulink仿真 (9)3.1 没有加高斯噪声的simulink仿真 (9)3.1.1电路图 (9)3.1.2参数设置 (10)3.1.3仿真结果 (13)3.2参加高斯噪声的simulink仿真 (15) (15) (16) (17) (17)4心得体会 (18)参考文献 (18)附录 (20)1 DSB 调制的根本原理在AM 信号中,载波分量并不携带信息,信息完全由边带传送。
AM 调制模型中将直流分量去掉,即可得到一种高调制效率的调制方式——抑制载波双边带信号,即双边带信号〔DSB 〕。
DSB 信号的时域表示式频谱:DSB 的时域波形和频谱如图1-1所示:t t m t s c DSB ωcos )()(=)]()([21)(c c DSB M M S ωωωωω-++=HH时域频域图1-1 DSB调制时、频域波形DSB的相干解调模型如图1-2所示::图1-2 DSB调制器模型与AM信号相比,因为不存在载波分量,DSB信号的调制效率时100%,DSB 信号解调时需采用相干解调。
DSB调制与解调的系统框图如图1-3所示:图1-3 DSB 调制与解调系统框图 2 DSB 调制与解调的MATLAB 实现如果将AM 信号中的载波抑制,只需在将直流0A 去掉,即可输出抑制载波双边带信号〔DSB-SC 〕。
DSB-SC 调制器模型如图2-1所示:图2-1 B-SC 调制器模型其中,设正弦载波为0()cos()c c t A t ωϕ=+ 式中,A 为载波幅度;c ω为载波角频率;0ϕ为初始相位〔假定0ϕ为0〕。
假定调制信号()m t 的平均值为0,与载波相乘,即可形成DSB-SC 信号,其时域表达式为 ()cos DSB c s m t t ω=调制信号 调制器信道 发送滤波接收滤波载波 解调器 噪声 低通滤波 解调信号式中,()m t 的平均值为0。
MATLAB 实现DSB 调制与解调
学生:黄文伯
班级:通信112
指导老师:文欢
一、研究的主要内容和研究的意义
通过本次课设更深入的了解DSB 调制和解调的基本原理以及利用MATLAB 软件对DSB 信号的调制解调,深入地理解调制解调技术在通信工程专业系列课程中的理论基础地位、作用和意义;加深对基本概念和基本原理的理解,并能够用所学知识进行调制解调仿真及性能分析。
二、DSB 调制与解调原理
DSB 是AM 调制的一种,AM 信号通过信道后自然会叠加有燥声,经过接收天线进入带通滤波器。
BPF 的作用有两个,一是让AM 信号直接通过,二是滤出带外噪声。
AM 信号通过BFP 后与本地载波相乘后。
进入LPF ,LPF 的截止频率设定为一个定值,它不允许频率大于截止频率的成分通过,因此LPF 的输出仅为与要的信号。
三、高斯白噪声
在实际信号传输过程中,通信系统不可避免的会遇到噪声,例如自然界中的各种电磁波噪声和设备本身产生的热噪声、散粒噪声等,它们很难被预测。
而且大部分噪声为随机的高斯白噪声,所以在设计时引入噪声,才能够真正模拟实际中信号传输所遇到的问题,进而思考怎样才能在接受端更好地恢复基带信号。
信道加性噪声主要取决于起伏噪声,而起伏噪声又可视为高斯白噪声,因此我在此环节将对双边带信号添加高斯白噪声来观察噪声对解调的影响情况。
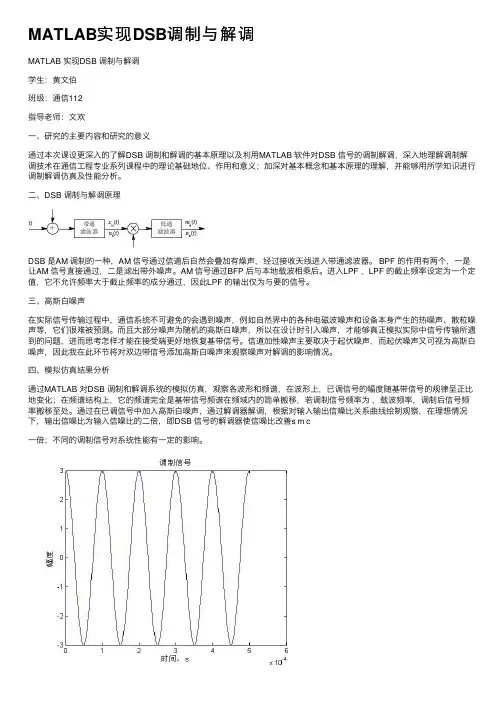
四、模拟仿真结果分析
通过MATLAB 对DSB 调制和解调系统的模拟仿真,观察各波形和频谱,在波形上,已调信号的幅度随基带信号的规律呈正比地变化;在频谱结构上,它的频谱完全是基带信号频谱在频域内的简单搬移,若调制信号频率为 ,载波频率,调制后信号频率搬移至处。
通过在已调信号中加入高斯白噪声,通过解调器解调,根据对输入输出信噪比关系曲线绘制观察,在理想情况下,输出信噪比为输入信噪比的二倍,即DSB 信号的解调器使信噪比改善s m c
一倍;不同的调制信号对系统性能有一定的影响。