平衡式旋转矩阵10中6保5

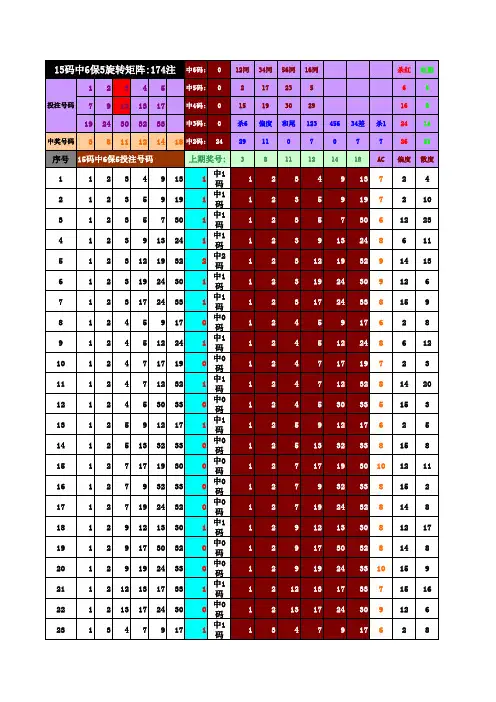
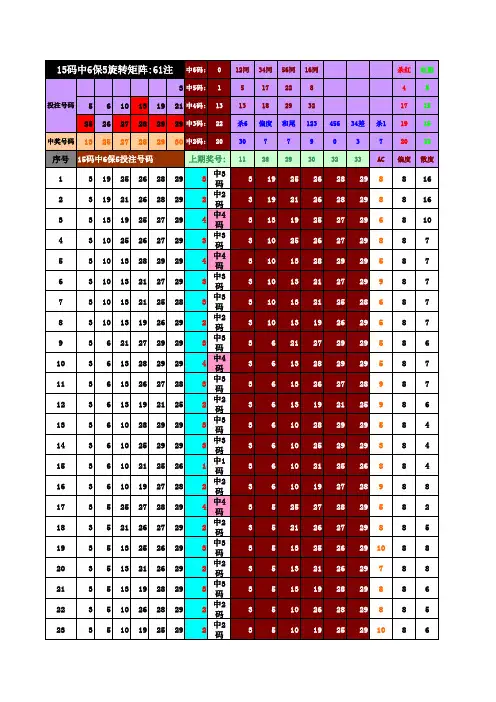
旋转矩阵中奖的秘诀旋转矩阵中奖的秘诀旋转矩阵中奖的秘诀在买彩过程中，最大的遗憾莫过于几乎选对了所有号码，但因为没有组合在一起，错过了中奖机会，现我将个人买彩心得与大家探讨。

第一步：如果我们选定了14个号码至18个之间（举例14个号码），可以按每两个号码结为一组，分别用字母A-G等7个字母表示，然后运用选五型矩阵出三保三组成5注如下：1.ABCFG；2.ABDFG；3.ABEFG；4.ACDEG；5.BCDEF。

第二步：将每注中的10个号码用出七保六组成8注，共40注，资金不强的彩民可以将每个复式用出七保五组成3注单式：也就是将步骤一的5注中的每一注也就是10个号码用出七保五来组成3个单注，五注复式可以拆分成15注单式，共计30元。

例如：五注中的1.ABCFG中10个号码分别用 a、 b、 c、 d、 e、 f、 g、 h、 i、 j 等10个字母来表示，则可拆：1.abcdehj，2.adefgij，3.bcefghi等三注单式。

有斩获过，有兴趣的彩民不妨一试，提高中奖率，最后祝愿大家中奖！在买彩过程中，最大的遗憾莫过于几乎选对了所有号码，但因为没有组合在一起，错过了中奖机会，现我将个人买彩心得与大家探讨。

第一步：如果我们选定了14个号码至18个之间（举例14个号码），可以按每两个号码结为一组，分别用字母A-G等7个字母表示，然后运用选五型矩阵出三保三组成5注如下：1.ABCFG；2.ABDFG；3.ABEFG；4.ACDEG；5.BCDEF。

第二步：将每注中的10个号码用出七保六组成8注，共40注，资金不强的彩民可以将每个复式用出七保五组成3注单式：也就是将步骤一的5注中的每一注也就是10个号码用出七保五来组成3个单注，五注复式可以拆分成15注单式，共计30元。

例如：五注中的1.ABCFG中10个号码分别用 a、 b、 c、 d、 e、 f、 g、 h、 i、 j 等10个字母来表示，则可拆：1.abcdehj，2.adefgij，3.bcefghi等三注单式。

什么是旋转矩阵有着怎样的性质导读：我根据大家的需要整理了一份关于《什么是旋转矩阵有着怎样的性质》的内容，具体内容：旋转矩阵解决的是如何组合集合中的元素以达到某种特定的要求。

那么你对旋转矩阵了解多少呢?以下是由我整理关于什么是旋转矩阵的内容，希望大家喜欢!什么是旋转矩阵旋转矩阵是...旋转矩阵解决的是如何组合集合中的元素以达到某种特定的要求。

那么你对旋转矩阵了解多少呢?以下是由我整理关于什么是旋转矩阵的内容，希望大家喜欢!什么是旋转矩阵旋转矩阵是世界上著名的彩票专家、澳大利亚数学家底特罗夫研究的，它可以帮助您锁定喜爱的号码，提高中奖的机会。

首先您要先选一些号码，然后，运用某一种旋转矩阵，将你挑选的数字填入相应位置。

如果您选择的数字中有一些与开奖号码一样，您将一定会中一定奖级的奖。

当然运用这种旋转矩阵，可以最小的成本获得最大的收益，且远远小于复式投注的成本。

旋转矩阵的原理在数学上涉及到的是一种组合设计：覆盖设计。

而覆盖设计，填装设计，斯坦纳系，t-设计都是离散数学中的组合优化问题。

它们解决的是如何组合集合中的元素以达到某种特定的要求。

其最古老的数学命题是寇克曼女生问题：某教员打算这样安排她班上的十五名女生散步：散步时三女生为一组，共五组。

问能否在一周内每日安排一次散步，使得每两名女生在一周内一道散步恰好一次?寇克曼于1847年提出了该问题，过了100多年后，对于一般形式的寇克曼问题的存在性才彻底解决。

用1~15这15个数字分别代表15个女生，其中的一组符合要求的分组方法是：星期日：(1，2，3)，(4，8，12)，(5，10，15)，(6，11，13)，(7，9，14)星期一：(1，4，5)，(2，8，10)，(3，13，14)，(6，9，15)，(7，11，12)星期二：(1，6，7)，(2，9，11)，(3，12，15)，(4，10，14)，(5，8，13)星期三：(1，8，9)，(2，12，14)，(3，5，6)，(4，11，15)，(7，10，13)星期四：(1，10，11)，(2，13，15)，(3，4，7)，(5，9，12)，(6，8，14)星期五：(1，12，13)，(2，4，6)，(3，9，10)，(5，11，14)，(7，8，15)星期六：(1，14，15)，(2，5，7)，(3，8，11)，(4，9，13)，(6，10，12)旋转矩阵的性质设是任何维的一般旋转矩阵:两个向量的点积在它们都被一个旋转矩阵操作之后保持不变: 从而得出旋转矩阵的逆矩阵是它的转置矩阵: 这里的是单位矩阵。

什么是旋转矩阵？一、名词解释【中6保5】比如你选择的10个红球复式中了6红,则经过旋转矩阵拆分后,一定能中5红,当然,仍有机会中6红；【中6保4】比如你选择的10个红球复式中了（4或5或6）红,则经过旋转矩阵拆分后,一定能中4红,当然,仍有机会中（5或6）红；【中5保5】比如你选择的10个红球复式中了（5或6）红,则经过旋转矩阵拆分后,一定能中5红,当然,仍有机会中6红；【中5保4】比如你选择的10个红球复式中了（4或5）红,则经过旋转矩阵拆分后,一定能中4红,当然,仍有机会中5红；二、旋转矩阵的由来旋转矩阵的核心就是用比较少的钱，合理组合彩票号码，提供中奖率。

美国人Ｇail Howard发明的'旋转矩阵'组合法造就了７４位大奖得主，这是一个算法很复杂且很有特色的组合方法。

这种方法的特点是：怎样花很少的钱将选中的号码组合在一起而减少遗漏。

如选１０个号码，如果采用复式投注则需１２０注，而在'旋转矩阵'中只用８－１２注就可覆盖其中的６个以上的号码。

但应该指出的是：这种方法也有它的缺陷，那就是虽然保住了中６个号码，但很容易漏掉大奖。

但比起复式投注大资金大范围捕鱼（有时还空手而归）的做法，明显具有稳扎稳打，投入少见效快的特点，特别适合工薪阶层的彩票玩家。

三、旋转矩阵的原理旋转矩阵详细了解：实际上，旋转矩阵并不是教如何选号的，而是教你如何科学地组合号码。

从它的别名“聪明组合”我们就可以知道了！站在数学角度看来，旋转矩阵属于一个典型的组合设计问题，进一步讲，是属于组合设计中的覆盖设计的问题。

四、旋转矩阵的使用旋转矩阵的使用过程是：（1）首先依据各种分析工具，确定若干个号码；（2）选择合适的组号规则(公式)，然后生成号码即可。

使用矩阵前，我们应确认要选择哪一组公式！应注意的是旋转矩阵的注数与你所选择的号码个数是呈级数关系的，你选择了更多的号码那么你的投入将大大的增加！当号码增加到一定的程度后如果不加入一定的条件，那么你的投入将可能是一个天文数字！投入与你能使用的号码个数及矩阵中奖保证是成正比的。

旋转矩阵的数学原理⼀、从寇克曼⼥⽣问题讲起旋转矩阵涉及到的是⼀种组合设计：覆盖设计。

⽽覆盖设计，填装设计，斯坦纳系，t-设计都是离散数学中组合优化问题。

它们解决的是如何组合集合中的元素以达到某种特定的要求。

为了使读者更容易明⽩这些问题，下⾯先从⼀道相当古⽼的数学名题讲起。

(⼀)寇克曼⼥⽣问题某教员打算这样安排她班上的⼗五名⼥⽣散步：散步时三名⼥⽣为⼀组，共五组。

问能否在⼀周内每⽇安排⼀次散步，使得每两名⼥⽣在这周内⼀道散步恰好⼀次？看起来题⽬似乎很简单，然⽽它的彻底解决并不容易。

事实上，寇克曼于1847年提出了该问题，过了100多年后，对于⼀般形式的寇克曼问题的存在性才彻底解决。

⽤1-15这15个数字分别代表这15个⼥⽣，下⾯给出⼀组符合要求的分组⽅法：星期⽇：(1，2，3)，(4，8，12)，(5，10,15)，(6，11,13)，(7，9，14)星期⼀：(1，4，5)，(2，8，10)，(3，13,14)，(6，9，15)，(7，11,12)星期⼆：(1，6，7)，(2，9，11)，(3，12,15)，(4，10,14)，(5，8，13)星期三：(1，8，9)，(2，12,14)，(3，5，6)，(4，11,15)，(7，10,13)星期四：(1，10,11)，(2，13,15)，(3，4，7)，(5，9，12)，(6，8，14)星期五：(1，12,13)，(2，4，6)，(3，9，10)，(5，11,14)，(7，8，15)星期六：(1，14,15)，(2，5，7)，(3，8，11)，(4，9，13)，(6，10,12)该问题就是最典型的组合设计问题。

其本质就是如何将⼀个集合中的元素组合成⼀定的⼦集系以满⾜⼀定的要求。

表⾯上看起来，寇克曼⼥⽣问题是纯粹的数学游戏，然⽽它的解却在医药试验设计上有很⼴泛的运⽤。

寇克曼⼥⽣问题是t-设计中很特殊的⼀类——可分解斯坦纳设计。

下⾯我会详细解释这⼏个名词的含义。

常用旋转矩阵组号方案此前我们介绍了旋转矩阵的原理，为了方便各位读者，我们总结了常用的旋转矩阵组合，在使用时只需将相应的号码按组合顺序排列，就可以完成组合方案。

下文中包含三类普通缩水组合，分别是中六保五型、中五保四型和中六保四型。

中六保五型缩水，是最传统的缩水方式，比较适合资金相对充裕的彩民。

红球复式中六个号码，最低中奖保证也是五个号码，如果能中5+1就是3000元，同时也未完全排除中大奖的可能，比较适合对大奖有一定期望的彩民。

由于可将原始复式缩减7至40倍，使得彩民在投注时有充裕的资金加大对蓝球的选择。

由于只中六个红球仅为二等奖回报不高，而蓝球每多选一个资金就要加上一倍，中六保五型缩水与复式投注相比，从回报上更为科学，毕竟中中等奖级的概率要远远超过中大奖的概率，对于投注者来说，使用中六保五型缩水能有效保护资金的安全性。

例如十六码红球组合多达8008注，而进行中六保五缩水后仅为224注，此时即使全包蓝球也不过是3584注，在原始复式全中的情况下至少能保住一注5+1（当然，我们也不建议蓝球全包，一次选择4个以内是比较科学的）。

有些彩民朋友可能会问，中6+0可以拿二等奖，而中5+1只能中三等奖3000元，这样划算吗？实际上，以十六码复式为例，选中6个号码的理论概率仅为0.72%，长期投注下去必然是吃不消的，因此我们没有必要把中6+0作为基本定位，中六保五型缩水的效率要远远高于复式投注。

中五保四型缩水，是最常用的缩水方式，也是相对来说最实用的缩水方式。

有经验的彩民朋友都知道，如果您的原始复式为16个号左右，最常遇到的是中四码和五码的组合，能圈中六码的机会实在是凤毛麟角。

因此，中六保X型缩水实际上并未收到完美成效。

而中五保四型缩水本身定位就是原始复式中五码，虽然中大奖的可能性不如中六保五型缩水，但是却能节省大量资金，例如十六码原始复式为8008注，中六保五型缩水为224注，而中五保四型缩水仅为54注。

如果您使用了中六保五型缩水，在原始复式只中五码的情况下，缩水结果通常也只能保住四码，因此两者效果几乎相同，区别仅仅在于中四码注数的波动。

实际上，旋转矩阵不是教你去如何选号的，而是教你如何科学地组合号码。

相比于复式投注、轮次矩阵等组合号码的方法，旋转矩阵有着投入低、中奖保证高的优点。

举个例子讲，10个号码的7，六型旋转矩阵的含义就是，你选择了10个号码，如果其中包含了7个中奖号码，那么运用该矩阵提供的8注号码，你至少有一注中对6个号码的奖。

本矩阵只要投入16元，而相应的复式投注需要投入240元。

大家知道，用10个号码，只购买其中的8注，如果你胡乱组合的话，即使这10个号码中包含有7个中奖号码，你也很可能只中得一注6个号码的奖的最低中奖保证。

旋转矩阵又叫覆盖设计。

对覆盖设计的研究始于19世纪，1835年J。

Plue Cker和W。

S。

B。

Wool House(1844)开始研究此类问题。

到了1969年，人们发现它对军队中布阵与战略设计以及计算机芯片设计都大有用途，因此得到了迅速发展。

在统计上，医药设计，农业试验，核研究，质量控制甚至在彩票中都大有用途。

许多组合数学家和计算数学专家都对覆盖设计的研究倾注了巨大的心血。

有一些彩票专家声称旋转矩阵（聪明组合）是其独特的发明，实际上几乎所有旋转矩阵都是数学家的劳动成果，而不是那些所谓的彩票专家所能研究出来的。

古老的寇克曼女生问题与旋转矩阵非常接近。

著名组合数学家寇克曼大约于100多年前提出了这样的问题：某教员打算这样安排她班上的十五名女生散步：散步时三名女生为一组，共五组。

为使每两个女生之间都有充分的交流机会，问如何在一周内每日安排一次散步，使得每两名女生在这周内一道散步恰好一次？这道问题看起来题目似乎很简单，然而它的彻底解决并不容易。

事实上，寇克曼于1847年进出了该问题的一般形式，过了100多年后，对于一般形式的寇克曼三元系的解的存在性才彻底解决。

不过这道例题的参数比较小，一般人只要假以时日，相信也会得到一个符合要求的答案。

用1-15这15个数字分别代表这15个女生，下面给出一组符合要求的分组方法：星期日：（1，2，3），（4，8，12），（5，10，15），（6，11，13），（7，9，14）星期一：（1，4，5），（2，8，10），（3，13，14），（6，9，15），（7，11，12）星期二：（1，6，7），（2，9，11），（3，12，15），（4，10，14），（5，8，13）星期三：（1，8，9），（2，12，14），（3，5，6），（4，11，15），（7，10，13）星期四：（1，10，11），（2，13，15），（3，4，7），（5，9，12），（6，8，14）星期五：（1，12，13），（2，4，6），（3，9，10），（5，11，14），（7，8，15）星期六：（1，14，15），（2，5，7），（3，8，11），（4，9，13），（6，10，12）该问题就是最典型的组合设计问题。

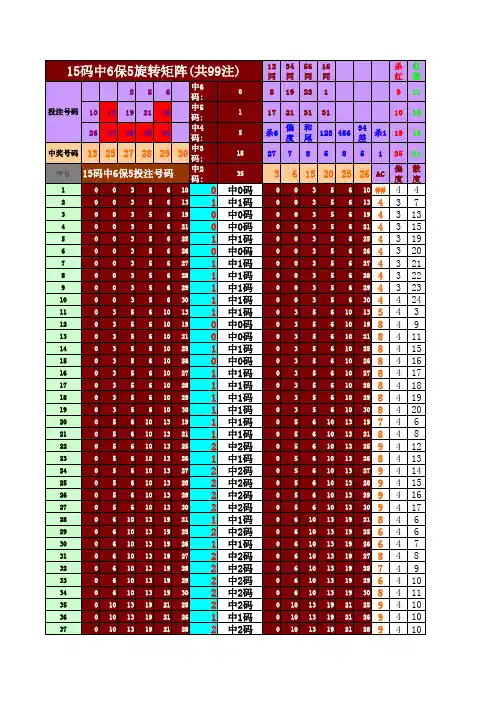
旋转矩阵转换法深入了解“旋转矩阵”<一>旋转矩阵是一种号码的组合方法，而不是选号方法。

旋转矩阵是根据数学的覆盖原理进行数字组合的一种方法，其核心是以最低的成本实现最大的效果。

而复式投注是以滴水不漏、无遗漏的全覆盖设计对数字的排列进行组合。

一种是经过优化了的组合，一种是全部的组合，对于乐透型彩票而言，复式投注由于组合形式毫无遗漏，因而只要所选的号码中含有中奖号码，有7+1个中7+1个，有7个中7个，依此类推，100％保证中奖；旋转矩阵则根据所使用的公式才能确定所中的号码个数。

“旋转矩阵”与复试投注是一种基于“旋转矩阵”数学原来构造的选号法，其核心宗旨是：以极低的成本实现复试投注的效果。

一个例子：比如你选了10个号码，不妨设为A，B，C，D，E，F，G ，H，J。

你想把他们组合起来进行投注，那么组合号码的方法一般有以下几种：1.复式投注最简单的方法无疑是复式投注，你只要购买这十个号码的复式就行了。

所需的注数是120注，成本是240元。

复式投注的好处是可以把这10个号码的所有组合一网打尽，也就是说，如果你选了这10个号码中包含了开出的7个基本号，你可以稳中一等奖。

但复式投注的缺点也是显而易见的，它的成本太高了，所以所选的号码个数很有限，如果超过12个号码就要超过3000元。

如果你不想花那么大的成本的话，比如只想花50元以内，那么你可以选用其他的组合号码的办法。

2.轮次矩阵轮次矩阵就是把每个号码都按顺序依次轮一遍，以如上的10个号码为例，轮次矩阵组合的10注如下：A，B，C，D，E，F，GB，C，D，E，F，G，HD，E，F，G，H，I，JE，F，G，H，I，J，AF，G，H，I，J，A，BG，H，I，J，A，B，CH，I，J，A，B，C，DI，J，A，B，C，D，EJ，A，B，C，D，E，F这种组合号码的方法成本很低，而且看过去很美观，把每个号码都排了7遍。

但实际上，这种组合号码的方法和胡乱组合一样，是很不可取的。

1需求分析通过对矩阵的学习，分析研究了矩阵相关的特性，从而确定了矩阵操作系统的定位和各方面的需求。

1.1功能需求分析矩阵操作主要包括三个操作，分别是矩阵翻转、矩阵卷动、矩阵旋转。

其中三个操作又包括不同的各自的特点操作。

矩阵的翻转包括水平翻转和垂直翻转。

矩阵卷动包括左右卷动和上下卷动，卷动的操作中又包含着卷动的位数的要求。

矩阵的旋转包括逆时针旋转和顺时针旋转，旋转的操作中包含着旋转的角度，需有90度、180度、270度、360度等类似的特殊的旋转角度的操作。

同时在课程的设计中要有对错误操作的提示信息。

以免输入发生了错误，运行出来错误的结果但不知是哪里出了问题。

对返回操作的设计也不容忽视，每个主操作和其子操作必要时需设立返回的操作。

矩阵操作的要求是编写代码，实现矩阵的翻转、卷动和旋转。

运行程序后，随机生成一个元素为三位正整数的5×5的矩阵，并显示如下面的参考界面：选择一个菜单后，要求输入操作的方向，行数或烈数，输入后，显示操作的结果。

1.2非功能需求分析课程设计是计算机科学与技术专业软件工程方向重要的一门专业基础课，内容庞大，涉及面广，知识点多，教、学难度都非常大，往往费了大量的时间而达不到预期的教学效果。

俗语说：学习的最好方法是实践。

本次设计正是基于此，力求通过一个理论联系实际的机会，通过一定难度的课题，独立完成。

通过实践，建立系统设计的整体思想，锻炼编写程序、调试程序的能力，学习文档编写规范，培养独立学习、吸取他人经验、探索前言知识的习惯。

同时，课程设计可以充分弥补课堂教学及普通实验中知识深度与广度有限的缺陷，更好地从全局角度把握课程体系。

课程设计要求我们：要充分认识到其重要性，认真做好各项准备工作；既要虚心接受老师的指导，又要充分发挥主观能动性，要结合课题，独立思考，努力钻研，勤于实践，勇于创新；收集资料，自学相关的知识，拓宽知识面，根据课题的基本要求，自行完成设计任务；按时、独立完成规定的工作任务，不弄虚作假，不抄袭他人；严格遵守学习和劳动纪律，不无故缺席，不迟到早退，不懈怠，不拖拉，要积极主动；严格要求自己，树立严肃、严密、严谨的科学态度，按时、按质、按量完成。

什么是旋转矩阵？2012-03-09 10:22:47 责任编辑：amber 来源：乐和彩点击次数：22927一、名词解释【中6保5】比如你选择的10个红球复式中了6红,则经过旋转矩阵拆分后,一定能中5红,当然,仍有机会中6红；【中6保4】比如你选择的10个红球复式中了（4或5或6）红,则经过旋转矩阵拆分后,一定能中4红,当然,仍有机会中（5或6）红；【中5保5】比如你选择的10个红球复式中了（5或6）红,则经过旋转矩阵拆分后,一定能中5红,当然,仍有机会中6红；【中5保4】比如你选择的10个红球复式中了（4或5）红,则经过旋转矩阵拆分后,一定能中4红,当然,仍有机会中5红；二、旋转矩阵的由来旋转矩阵的核心就是用比较少的钱，合理组合彩票号码，提供中奖率。

美国人Ｇail Howard发明的"旋转矩阵"组合法造就了７４位大奖得主，这是一个算法很复杂且很有特色的组合方法。

这种方法的特点是：怎样花很少的钱将选中的号码组合在一起而减少遗漏。

如选１０个号码，如果采用复式投注则需１２０注，而在"旋转矩阵"中只用８－１２注就可覆盖其中的６个以上的号码。

但应该指出的是：这种方法也有它的缺陷，那就是虽然保住了中６个号码，但很容易漏掉大奖。

但比起复式投注大资金大范围捕鱼（有时还空手而归）的做法，明显具有稳扎稳打，投入少见效快的特点，特别适合工薪阶层的彩票玩家。

三、旋转矩阵的原理旋转矩阵详细了解：实际上，旋转矩阵并不是教如何选号的，而是教你如何科学地组合号码。

从它的别名“聪明组合”我们就可以知道了！站在数学角度看来，旋转矩阵属于一个典型的组合设计问题，进一步讲，是属于组合设计中的覆盖设计的问题。

四、旋转矩阵的使用旋转矩阵的使用过程是：（1）首先依据各种分析工具，确定若干个号码；（2）选择合适的组号规则(公式)，然后生成号码即可。

使用矩阵前，我们应确认要选择哪一组公式！应注意的是旋转矩阵的注数与你所选择的号码个数是呈级数关系的，你选择了更多的号码那么你的投入将大大的增加！当号码增加到一定的程度后如果不加入一定的条件，那么你的投入将可能是一个天文数字！投入与你能使用的号码个数及矩阵中奖保证是成正比的。

旋转矩阵原理及在彩票投注中的运用经过数学界多年的研究，人们找出了一种组合号码的全新方法——被称之为旋转矩阵。

用此方法进行投注的话，轮次矩阵中出现的情况是永远不会出现的。

其意义在于，如果你所选择的多个号码中包括了开奖的号码，那么你只要用很少的投入，就能够得到一个相应级别的中奖保证。

具体你的投入的多少与你选择号码的个数、包含中奖号码的个数以及你所期望的中奖保证相关。

实际上，旋转矩阵不是教你去如何选号的，而是教你如何科学地组合号码。

相比于复式投注、轮次矩阵等组合号码的方法，旋转矩阵有着投入低、中奖保证高的优点。

举个例子讲，10个号码的7，六型旋转矩阵的含义就是，你选择了10个号码，如果其中包含了7个中奖号码，那么运用该矩阵提供的8注号码，你至少有一注中对6个号码的奖。

本矩阵只要投入16元，而相应的复式投注需要投入240元。

大家知道，用10个号码，只购买其中的8注，如果你胡乱组合的话，即使这10个号码中包含有7个中奖号码，你也很可能只中得一些小奖。

而运用旋转矩阵的话，就可以得到一个对6个号码的奖的最低中奖保证。

从纯数学角度看，旋转矩阵属于一个典型的组合设计问题，严格地讲，是属于组合设计中的覆盖设计的问题。

如何才能找到最少的注数以保证全面的覆盖是一个历时已久的数学难题，与旋转矩阵相关的数学问题还有很多，比如填装设计、斯坦纳设计、t-设计等等，这些问题都是数学界长期以来的难题，在军事上和医药实验上都有着广泛的运用。

当然把高深的数学原理运用在彩票这一极其通俗的事物上，也是一个历史的玩笑。

好在对于一般运用旋转矩阵的彩民来讲，其背后高深的数学原理一点也不会成为运用的障碍，因为我们需要的只是知道如何运用就够了。

目前，对旋转矩阵的解法，数学界还没有找到一个通用的公式，大部分的设计即使用最先进的超级电脑也很难求出，全盘搜索的算法耗用的时间将会是一个天文数字。

好在人们找到了一种全新的模拟算法，它大大提高了求解覆盖设计的速度，但它不能保证找到的覆盖设计一定是最小的覆盖设计。