- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
xik
xik xk , i 1,2,, n; k 1,2,, p. sk 2 n 1 n 1 2 xk xik , S K ( xik xk ) n i 1 N 1 i 1
5 方差加权距离
x 标准化数据 ik 的欧氏距离就是方差加权距离。
p ( xik x jk ) 2 d ( xi x j ) 2 s k k 1
p
3 Minkowski距离
其中m≥1,又称为Lm距离。 4 Chebyshev距离
d ( xi , x j ) max xik x jk
1 k p
。
是Minkowski距离当m→+∞时的极限
由于不同指标通常有不同的量纲,这会引起各取值的分散程度差异 较大,有时会造成很不合理的结果,为了消除此种影响,常需要在 分析前对数据进行标准化处理。
联系 判别分析中的训练样本往往是从聚类
分析中得到的
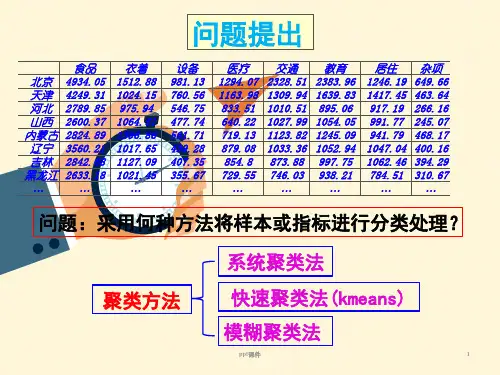
引入:如何度量远近?
如果想要对 100个学生进行分类,如果仅仅知道 他 们的数学成绩,则只好按照数学成绩来分类; 这些成绩在直线上形成100个点。这样就可以把接 近的点放到一类。 如果还知道他们的物理成绩,这样数学和物理成 绩就形成二维平面上的100个点,也可以按照距离 远近来分类。 三维或者更高维的情况也是类似;只不过三维以 上的图形无法直观地画出来而已。
样品间相似性的度量
T ( X , X , , X ) 设X= 1 2 为所关心的p个指 标, P
对此指标作n次观测得n组观测值
xi ( xi1, xi 2 ,, xip ) , i 1,2,n
T
称这n组观测数据为n个样品。这样,每个样 品可看成p维空间的一个点,n个样品组成p维 空间的n个点,我们可以用各点之间的距离来衡 量个样品点之间的靠近程度。
?
通常都是尝试各种不同距离分析, 最终采用最有利于分类的距离定 义。
令
dij d ( xi , x j ), D (dij )n*n 形成n个样品
两两之间的距离矩阵:
d12 0 dn2 d1n d2n d nn
x1, x2 ,, xn
0 d 21 d n1
其中
dij d ji
快速聚类分析及实例
思想:首先将样品粗糙得分类,然后再依据 样品间的距离按一定规则逐步调整,直至不能 再调整为止。 适合于:样本数目较大的数据集的聚类分析 局限性:需要事先指定分类的数目,而且此 数目对最终分类结果有较大影响。
解决办法:实际中一 般要对多个分类的数 目进行尝试,以找出 合理的分类结果
快速聚类法的步骤
(1)随机选择聚类种子点或中心点; (2)将每个观察样本分配给最近的种子; (3)重新把每个聚集中的中心点作为种子; (4)不断重复上述过程直到种子的变化
足够小为止。
快速聚类法的步骤
1.设k个初始聚点的集合是 L(0) x1(0) , x2(0) ,xk (0)
用下列原则实现初始分类:
广义的“距离”: 1 欧氏距离 2 绝对距离
p 2 d ( xi , x j ) ( xik x j ) xik x jk
k 1
m p d ( xi , x j ) xik x jk k 1 1 m
1 2
6 马氏距离
T 1 d ( xi x j ) ( xi x j ) S ( xi x j )
[
]
1 2
其中S是由样品 x1 , x2 , , xn算得的协方差矩阵: 1 S ( xi x )( xi x ) n 1 i 1
n T
1 n 其中x xi n i 1
( 0)
Gi x : d ( x, xi ) d ( x, x j ), j 1,2,, k , j i , i 1,2,, k
这样,将样品分成不相交的k类,以上初始分类的原则是 每个样品以最近的初始聚点归类,这样得到一个初始分 类
( 0)
( 0)
G(0) G1 , G2 ,, Gk
( 0)
( 0)
( 0)
2.从
G
( 0)
出发,计算新的聚点集合
L
(1)
,以 Gi
( 0)
的重心作为新的聚点: 1 ( 0) xi xl , i 1,2,, k n xl Gi ( 0) 其中
ni
是类
(1)
Gi
( 0)
(1) 1
L x , x2 ,xk
(1) L 从
(1)
1 选择聚点(聚类中心点)
• 经验选择 • 将n个样品人为地(或随机地)分为k类, 以每类的均值向量(称为重心)作为聚点。 • 最大最小原则
先选择所有样品中相距 最远的两个样品为初始 的两个聚点,然后,选择 第3个聚点(与前两个聚 点的距离最小者 ), 按相 同的原则依次选取下去, 直至选出k个聚点。
聚类分析的介绍 基本思想是:通过定义样品或变量间“接 近程度”的度量,以此为基础,将“相近” 的样品或变量归为一类 。
• 聚类分析和判别分析是研究分类问题 的数据分析方法。 • 聚类分析和判别分析的比较 聚类分析
进行聚类分析 前对总体有几 区别 种类型并不知 道
判别分析
总体分类已给定, 在总体分布或来自 总体训练样本基础 上,对新样品判定 属于哪个总体
目录
聚类分析 样品间相似性的度量 快速聚类分析及实例
分类
•俗语说,物以类聚、人以群分。 •但什么是分类的根据呢? •比如,要想把中国的县分成若干类,就有很 多种分类法; •可以按照自然条件来分, •比如考虑降水、土地、日照、湿度等各方面; •也可以考虑收入、教育水准、医疗条件、基 础设施等指标; •既可以用某一项来分类,也可以同时考虑多 项指标来分类。
中的样品数。这样,得到新的聚点集合
(1) (1)
Gi x : d ( x, xi ) d ( x, x j ), j 1,2,, k , j i , i 1,2,, k