全等三角形必考题型

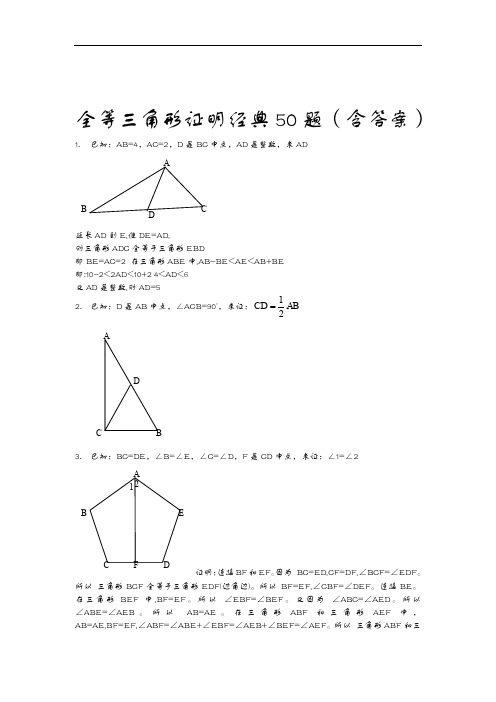
全等三角形证明经典50题（含答案）1.已知：AB=4 , AC=2 , D 是BC 中点，AD 是整数，求 AD延长AD 至U E,使DE=AD, 则三角形ADC 全等于三角形EBD即 BE=AC=2 在三角形 ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数，则AD=512.已知：D 是 AB 中点，/ ACB=90 °，求证： CD - AB2为BC=ED,CF=DF, / BCF= / EDF 。

所以 三角形BCF 全等于三角形 EDF （边角边）。

所以BF=EF, / CBF= / DEF 。

连接 BE 。

在三角形 BEF 中,BF=EF 。

所以 / EBF= / BEF 。

/ ABE= / AEB 。

所以 AB=AE 。

在三角形 ABF 和 / ABF= / ABE+ / EBF= / AEB+ / BEF= / AEF 。

所以/ C= / D , F 是 CD 中点，求证：/ 1 = / 2证明：连接BF 和EF 。

因又因为 / ABC= / AED 。

所以 三角形 AEF 中， AB=AE,BF=EF, 三角形ABF 和三角形AEF 全等。

所以 / BAF= / EAF （ / 仁/ 2）。

A3因为 EB = EF ,CE = CE ， 所以△ CEBCEF 所以/ B = / CFE 因为/ B +/ D = 180° / CFE + / CFA = 180° 所以/ D = / CFA 因为 AC 平分/ BAD 所以/ DAC = / FAC 又因为 AC = AC 所以△ ADC 也厶AFC ( SAS ) 所以AD = AF 所以AE = AF + FE = AD + BE12.如图，四边形 ABCD 中，AB // DC ，BE 、CE 分别平分/ ABC 、/ BCD ，且点 E 在AD 上。

全等三角形证明经典50题（含答案）1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2ADBC证明：连接BF 和EF 。

因为BC=ED,CF=DF,∠BCF=∠EDF。

所以 三角形BCF 全等于三角形EDF(边角边)。

所以 BF=EF,∠CBF=∠DEF。

连接BE 。

在三角形BEF 中,BF=EF 。

所以 ∠EBF=∠BEF。

又因为 ∠ABC=∠AED。

所以 ∠ABE=∠AEB。

所以 AB=AE 。

在三角形ABF和三角形AEF中，AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF。

所以 三角形ABF 和三角形AEF 全等。

所以∠BAF=∠EAF (∠1=∠2)。

4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC 证明：过E 点，作EG//AC ，交AD 延长线于G 则∠DEG=∠DCA，∠DGE=∠2又∵CD=DE ∴⊿ADC≌⊿GDE（AAS）BACDF2 1 E∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C证明：在AC 上截取AE=AB ，连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ，AD=AD ∴⊿AED≌⊿ABD （SAS ）∴∠AED=∠B ，DE=DB∵AC=AB+BDAC=AE+CE ∴CE=DE∴∠C=∠EDC∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE 证明：在AE 上取F ，使EF ＝EB ，连接CF 因为CE⊥AB所以∠CEB＝∠CEF＝90° 因为EB ＝EF ，CE ＝CE ， 所以△CEB≌△CEF所以∠B ＝∠CFE因为∠B ＋∠D ＝180°，∠CFE＋∠CFA＝180° 所以∠D＝∠CFA 因为AC 平分∠BAD所以∠DAC＝∠FAC又因为AC ＝AC所以△ADC≌△AFC（SAS ） 所以AD ＝AF 所以AE ＝AF ＋FE ＝CDB AAD ＋BE12. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

1.下列哪个条件不能单独用来证明两个三角形全等？A.SSS（三边相等）B.SAS（两边及夹角相等）C.AAA（三角相等）（答案）D.ASA（两角及夹边相等）2.已知三角形ABC和三角形DEF，AB=DE，BC=EF，∠B=∠E，则这两个三角形全等吗？A.是（答案）B.否3.若两个三角形有两对相等的角和一对相等的边，且相等的边不是这两个相等角的夹边，则这两个三角形全等吗？A.是B.否（答案）4.在证明两个三角形全等时，至少需要几个元素对应相等？A.1个B.2个C.3个（答案）D.4个5.下列哪组条件可以证明三角形ABC和三角形DEF全等？A.AB=DE，BC=EF，∠A=∠DB.AB=DE，BC=DF，∠B=∠E（答案）C.∠A=∠D，∠B=∠E，∠C=∠FD.AB=DE，AC=DF，∠B=∠E6.已知三角形ABC和三角形DEF中，AB=DE，∠A=∠D，若证这两个三角形全等，还需要什么条件？A.∠B=∠EB.∠C=∠FC.BC=EF（答案）D.AC=DF7.在三角形ABC和三角形DEF中，如果AB=DE，BC=EF，且∠A=∠D，那么这两个三角形一定全等吗？A.是（答案）B.否8.下列哪个不是三角形全等的判定定理？A.HL定理（直角三角形的斜边和一条直角边相等）B.SSS定理（三边相等）C.AAA定理（三角相等）（答案）D.SAS定理（两边及夹角相等）9.已知三角形ABC和三角形DEF中，∠A=∠D，∠B=∠E，若证这两个三角形全等，还需要什么条件？A.AB=DE（答案）B.BC=EFC.AC=DFD.∠C=∠F10.在证明两个三角形全等时，如果已知两对相等的角和一对非夹边的相等边，那么这两个三角形一定全等吗？A.是B.否（答案）。

全等三角形证明经典50题（含答案）1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB从D 做辅助线3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。

因为 BC=ED,CF=DF,∠BCF=∠EDF 。

所以 三角形BCF 全等于三角形EDF(边角边)。

所以 BF=EF,∠CBF=∠DEF 。

连接BE 。

在三角形BEF 中,BF=EF 。

所以 ∠EBF=∠BEF 。

又因为 ∠ABC=∠AED 。

所以 ∠ABE=∠AEB 。

所以 AB=AE 。

在三角形ABF 和三角形AEF 中，AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。

所以 三角形ABF 和三角形AEF 全等。

所以 ∠BAF=∠EAF (∠1=∠2)。

ADBC4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC证明：过E 点，作EG//AC ，交AD 延长线于G 则∠DEG=∠DCA ，∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE （AAS ）∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C证明：在AC 上截取AE=AB ，连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ，AD=AD ∴⊿AED ≌⊿ABD （SAS ）∴∠AED=∠B ，DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE证明： 在AE 上取F ，使EF ＝EB ，连接CF 因为CE ⊥AB 所以∠CEB ＝∠CEF ＝90° 因为EB ＝EF ，CE ＝CE ， 所以△CEB ≌△CEF 所以∠B ＝∠CFE 因为∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180° 所以∠D ＝∠CFA 因为AC 平分∠BAD 所以∠DAC ＝∠FAC 又因为AC ＝AC 所以△ADC ≌△AFC （SAS ） 所以AD ＝AF 所以AE ＝AF ＋FE ＝AD ＋BE12. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

全等三角形的常见题型一、全等三角形的性质：1、如图，△ABC ≌△ADE ，则，AB= ．若∠BAE=120°，∠BAD=40°，则∠BAC= °．2、如图，△ECD ≌△BCA ，AC ⊥BD 于C ，AB=5 cm ，∠B=60°，则DE= 。

3、已知，如图ΔABE ≌ΔACD ，AB=AC ，BE=CD ，∠B=50°，∠AEC=120°，则∠DAC 的度数为（ ）A. 120°B. 70°C. 60°D.50°4、如图，ΔABC ≌ΔADE ，AB=AD ， AC=AE ，∠B=28º，∠E=95º，∠EAB=20º， 则∠BAD 为（ ）A.75ºB. 57ºC. 55ºD. 77º5、如图，ΔABC ≌ΔBAD ，A 和B ，C 和D 是对应顶点，如果AB=6cm ，BD=5cm ，AD=4cm ，那么BC 等于（ ）A ．6cm B.5cm C.4cm D.5cm 或4cm6、如图, ΔABC ≌ΔADE,AB 和AD,AC 和AE 是对应边,那么∠DAC 等于 A.∠ACB B.∠CAE C.∠BAE D.∠BAC7、已知图2中的两个三角形全等，则∠ 度数是（ ）A.72°B.60°C.58°D.50° 8、如图，Rt △ABC 中，∠ACB =90°，∠A =50°，将其折叠，使点A 落在边CB 上A ′处，折痕为CD ，则∠A ′DB =( ) (A)40°． (B)30°． (C)20°． (D)10°．9、如图所示，△ABE 和△ADC 是△ABC 分别沿着AB ，AC 边翻折180°形成的，若∠1∶∠2∶∠3=28∶5∶3，则∠α的度数为A ．80°B ．100°C ．60°D ．45°．A 'B DAC ABCDEADEBCABCDCBAED10、如图,在正方形ABCD中,E是AD的中点,F是BA延长线上的一点,AF=AB,已知△ABE≌△ADF.⑴在图中,可以通过平移、翻折、旋转中的哪一种方法，使△ABE变到△ADF的位置；⑵线段BE与DF有什么关系？证明你的结论.二、全等三角形判定SSSC DB CDD如图，已知点E C，在线段BF上，BE=CF，AB=DE，AC=DF．求证：ABC DEF△≌△．如图，A C＝B D，CB＝A D．求证：∠BAD＝∠ABC．已知:如图,AD=BC,AC=BD.求证:OD=OCCEB FDAOD CAADBFECA BCFECA BDE三、全等三角形判定SAS已知AD AE AB AC ==，．试说明：B C =∠∠；（江津区）如图，在△ABE 中，AB ＝AE,AD ＝AC,∠BAD ＝∠EAC, BC 、DE 交于点O. 求证： △ABC ≌△AED ；如图，△ABC 中，∠C=90度，AC=BC ，D 为AB 中点，AE=CF ， 求证：DE=DF ，四边形CEDF 面积为定值在ABC △中，AB AC =，点D 是直线BC 上一点（不与B C 、重合），以AD 为一边在AD 的右侧．．作ADE △，使AD AE DAE BAC =∠=∠，，连接CE ．（1）如图1，当点D 在线段BC 上，如果90BAC ∠=°，则BCE ∠= 度； （2）设BAC α∠=，BCE β∠=．O C EBD A FE D CB AA BC D E①如图2，当点D 在线段BC 上移动，则αβ，之间有怎样的数量关系？请说明理由； ②当点D 在直线BC 上移动，则αβ，之间有怎样的数量关系？请直接写出你的结论．已知Rt ABC △中，90AC BC C D ==︒，∠，为AB 边的中点，90EDF ∠=°，EDF ∠绕D 点旋转，它的两边分别交AC 、CB （或它们的延长线）于E 、F ． 当EDF ∠绕D 点旋转到DE AC ⊥于E 时（如图1），易证12DEF CEF ABC S S S +=△△△．当EDF ∠绕D 点旋转到DE AC 和不垂直时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，DEF S △、CEF S △、ABC S △又有怎样的数量关系？请写出你的猜想，不需证明．（2009年重庆）如图，在等腰Rt ABC △中，908C AC ∠==°，，F 是AB 边上的中点，点D 、E 分别在AC 、BC 边上运动，且保持AD CE =．连接DE 、DF 、EF ．在此运动变化的过程中，下列结论： ①DFE △是等腰直角三角形； ②四边形CDFE 不可能为正方形， ③DE 长度的最小值为4；④四边形CDFE 的面积保持不变； ⑤△CDE 面积的最大值为8． 其中正确的结论是（ ） A ．①②③ B ．①④⑤ C ．①③④ D ．③④⑤A EEA C C DB B 图1 图2 A A 备用图 BC B C备用图 AE CF BD图1图3ADFECBADBCE 图2F如图，扇形ODE 的圆心角为120，正三角形ABC 的中心恰好为扇形ODE 的圆心，且点B 在扇形ODE 内.(1)请连接OA OB 、，并证明AOF BOG △≌△；(2)求证：ABC △与扇形ODE 重叠部分的面积等于ABC △面积的13．如图：在△ABC 中，BE 、CF 分别是AC 、AB 两边上的高，在BE 上截取BD=AC ，在CF 的延长线上截取CG=AB ，连结AD 、AG 。

全等三角形证明经典50题（含答案）1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。

因为 BC=ED,CF=DF,∠BCF=∠EDF 。

所以 三角形BCF 全等于三角形EDF(边角边)。

所以 BF=EF,∠CBF=∠DEF 。

连接BE 。

在三角形BEF 中,BF=EF 。

所以 ∠EBF=∠BEF 。

又因为 ∠ABC=∠AED 。

所以 ∠ABE=∠AEB 。

所以 AB=AE 。

在三角形ABF 和三角形AEF 中，AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。

所以 三角形ABF 和三角形AEF 全等。

所以 ∠BAF=∠EAF (∠1=∠2)。

ADBC4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC 证明：过E 点，作EG//AC ，交AD 延长线于G 则∠DEG=∠DCA ，∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE （AAS ）∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C证明：在AC 上截取AE=AB ，连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ，AD=AD ∴⊿AED ≌⊿ABD （SAS ）∴∠AED=∠B ，DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE ∴∠C=∠ED C ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE证明： 在AE 上取F ，使EF ＝EB ，连接CF 因为CE ⊥AB 所以∠CEB＝∠CEF ＝90° 因为EB ＝EF ，CE ＝CE ， 所以△CEB ≌△CEF 所以∠B ＝∠CFE 因为∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180° 所以∠D ＝∠CFA 因为AC 平分∠BAD 所以∠DAC ＝∠FAC 又因为AC ＝AC 所以△ADC ≌△AFC （SAS ） 所以AD ＝AF 所以AE ＝AF ＋FE ＝AD ＋BE12. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

全等三角形经典题型全等三角形是几何学中的一个重要概念，它指的是具有相同形状和大小的两个三角形。

在解决全等三角形的经典题型时，我们通常会利用全等三角形的性质和一些几何定理来推导和证明。

以下是一些经典的全等三角形题型以及解题思路：1. SSS（边-边-边）判定法，当两个三角形的三条边分别相等时，可以判定两个三角形全等。

例如，已知三角形ABC和三角形DEF，且AB=DE，BC=EF，AC=DF，那么可以得出三角形ABC全等于三角形DEF。

2. SAS（边-角-边）判定法，当两个三角形的两边和夹角分别相等时，可以判定两个三角形全等。

例如，已知三角形ABC和三角形DEF，且AB=DE，BC=EF，∠BAC=∠EDF，那么可以得出三角形ABC 全等于三角形DEF。

3. ASA（角-边-角）判定法，当两个三角形的两角和一边分别相等时，可以判定两个三角形全等。

例如，已知三角形ABC和三角形DEF，且∠BAC=∠EDF，∠ABC=∠DEF，AC=DF，那么可以得出三角形ABC全等于三角形DEF。

4. RHS（直角边-斜边-直角边）判定法，当两个直角三角形的一个直角边和斜边分别相等时，可以判定两个三角形全等。

例如，已知直角三角形ABC和直角三角形DEF，且∠BAC=∠EDF，AC=DF，AB=DE，那么可以得出三角形ABC全等于三角形DEF。

5. AAS（角-角-边）判定法，当两个三角形的两角和一边的对应边分别相等时，可以判定两个三角形全等。

例如，已知三角形ABC和三角形DEF，且∠BAC=∠EDF，∠ABC=∠DEF，AB=DE，那么可以得出三角形ABC全等于三角形DEF。

在解决全等三角形题型时，我们要注意使用合适的判定法，并根据题目给出的已知条件进行推导和证明。

同时，还要注意运用其他几何定理和性质，如平行线的性质、垂直线的性质、等腰三角形的性质等，来辅助解题。

以上是关于全等三角形经典题型的回答，希望对你有所帮助。

全等三角形证明经典50题（含答案）1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。

因为 BC=ED,CF=DF,∠BCF=∠EDF 。

所以 三角形BCF 全等于三角形EDF(边角边)。

所以 BF=EF,∠CBF=∠DEF 。

连接BE 。

在三角形BEF 中,BF=EF 。

所以 ∠EBF=∠BEF 。

又因为 ∠ABC=∠AED 。

所以 ∠ABE=∠AEB 。

所以 AB=AE 。

在三角形ABF 和三角形AEF 中，AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。

所以 三角形ABF和三ADBC角形AEF 全等。

所以 ∠BAF=∠EAF (∠1=∠2)。

4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC证明：过E 点，作EG//AC ，交AD 延长线于G 则∠DEG=∠DCA ，∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE （AAS ）∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DG E ∴EF=EG ∴EF=AC5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C证明：在AC 上截取AE=AB ，连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ，AD=AD ∴⊿AED ≌⊿ABD （SAS ）∴∠AED=∠B ，DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE ∴∠C=∠E DC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE证明： 在AE 上取F ，使EF ＝EB ，连接CF 因为CE ⊥AB 所以∠CEB ＝∠CEF ＝90° 因为EB ＝EF ，CE ＝CE ， 所以△CEB ≌△CEF 所以∠B ＝∠CFE 因为∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180° 所以∠D ＝∠CFA 因为AC 平分∠BAD 所以∠DAC ＝∠FAC 又因为AC ＝AC 所以△ADC ≌△AFC （SAS ） 所以AD ＝AF 所以AE ＝AF ＋FE ＝AD ＋BE12. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

全等三角形是初中数学中的一个重要知识点，其常见题型主要有以下五种：
1. 已知两边及其夹角，求证全等：这是全等三角形最基本的题型，也是最常见的题型。

解题的关键在于理解全等三角形的定义，即两个三角形如果它们的三边分别相等，那么这两个三角形就是全等的。

在解答这类题目时，我们通常会使用SAS（边角边）或ASA（角边角）定理。

2. 已知一边及其对角，求证全等：这类题目的解题思路与第一种类似，但是需要用到的是AAS（角角边）定理。

在解答这类题目时，我们需要先找出两个三角形的对应角和对应边，然后利用AAS定理进行证明。

3. 已知两角及其夹边，求证全等：这类题目的解题思路与前两种有所不同，需要用到的是HL（直角边边）定理。

在解答这类题目时，我们需要先找出两个三角形的对应角和对应边，然后利用HL定理进行证明。

4. 已知一边及其高，求证全等：这类题目的解题思路与前三种有所不同，需要用到的是SSS （边边边）定理。

在解答这类题目时，我们需要先找出两个三角形的对应边，然后利用SSS 定理进行证明。

5. 已知一边及其中线或高线，求证全等：这类题目的解题思路与第四种相似，但是需要用到的是RHS（旋转、平移、缩放）定理。

在解答这类题目时，我们需要先找出两个三角形的对应边和对应的中线或高线，然后利用RHS定理进行证明。

以上就是全等三角形的五种常见题型，每种题型都有其特定的解题方法和技巧。

在解答这类题目时，我们需要灵活运用全等三角形的各种定理，同时也需要注意观察和分析题目中的条件，以便找到最合适的解题方法。

一、补充条件型试题[例1] （1）（06湖北宜昌课改）如图，AB=CD,AD 、BC 相交于点O ，要使△ABO ≌△DCO 。

应添加的条件为__________（添加一个条件即可）∠A=∠B,∠A=∠C ，∠B=∠C ，∠B=∠D ，AB ∥CD￥(2)(05重庆中考题) 如图，已知∠ACB=∠DBC ，要使△ABC ≌△DCB ，只需增加的一个条件是__________。

（只需填写一个你认为合适的条件即可）BD=CA,∠ABD=∠ACD,∠ABC=∠DCB,∠A=∠D ，S △ABO=S △CDO(3)(06深圳中考题) 如图，已知，在△ABC 和△DCB 中，AC=DB,若不增加任何字母与辅助线，要使△ABC ≌△DCB ，则还需要增加的一个条件是__________ AB=CD,或∠BCA=∠CBD(4)（04四川中考）如图，D 在AB 上，E 在AC 上，且∠B=∠C ，那么补充下列一个条件后，仍然无法判断△ABE ≌△ACD 的是（ ） =AE B.∠AEB=∠ADC =CD =AC 补充两个三角形中任意一组对应边相等即可，选B 二、\三、组合条件型试题[例2] （05杭州中考）如图，在△ABC 和△DEF 中，B 、E 、C 、F 在同一直线上，下面有四个条件，请你在其中选3个座位题设，余下的一个作为结论，下一个真命题，加以ABOC DA DB C| A D B C A DBADE、证明：①AB=DE ②AC=DF ③∠ABC=∠DEF ④BE=CF【解析：若所选条件中含有③∠ABC=∠DEF ，则另外两个条件可选择①AB=DE ④BE=CF ，证明全等的理由是边角边定理。

此时的真命题是：在△ABC 和△DEF 中，B,E,C,F 在同一直线上，若∠ABC=∠DEF,AB=DE,BE=CF,则AC=DF.若所选条件中不含有③∠ABC=∠DEF ，则另外三个条件也可构成一个真命题，此时证明全等的理由是边边边定理。

全等三角形证实经典50题（含答案） 1. 已知：AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延伸AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE即:10-2<2AD<10+2 4<AD<6又AD 是整数,则AD=52. 已知：D 是AB 中点,∠ACB=90°,求证：12CD AB3. 已知：BC=DE,∠B=∠E,∠C=∠D,F 是CD 中点,求证：∠1=∠2证实：衔接BF 和EF. 因为AD BCBC=ED,CF=DF,∠BCF=∠EDF. 所以 三角形BCF 全等于三角形EDF(边角边). 所以 BF=EF,∠CBF=∠DEF. 衔接BE. 在三角形BEF 中,BF=EF. 所以 ∠EBF=∠BEF. 又因为 ∠ABC=∠AED. 所以 ∠ABE=∠AEB. 所以 AB=AE. 在三角形ABF 和三角形AEF 中, AB=AE,BF=E F, ∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF. 所以 三角形ABF 和三角形AEF 全等. 所以∠BAF=∠EAF (∠1=∠2).4. 已知：∠1=∠2,CD=DE,EF//AB,求证：EF=AC 证实： 过E 点,作EG//AC,交AD 延伸线于G则∠DEG=∠DCA,∠DGE=∠2 又∵CD=DE ∴⊿ADC≌⊿GDE （AAS ） ∴EG=AC ∵EF//AB ∴∠DFE=∠1 ∵∠1=∠2 ∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知：AD 等分∠BAC,AC=AB+BD,求证：∠B=2∠C证实： 在AC 上截取AE=AB,衔接ED ∵AD 等分∠BAC ∴∠EAD=∠BAD 又∵AE=AB,AD=AD ∴⊿AED≌⊿ABD （SAS ） ∴∠AED=∠B,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知：AC 等分∠BAD,CE ⊥AB,∠B+∠D=180°,求证：AE=AD+BE 证实： 在AE 上取F,使EF ＝EB,衔接CF 因为CE⊥AB 所以CD B AB AC DF 2 1 E∠CEB＝∠CEF＝90° 因为EB ＝EF,CE ＝CE, 所以△CEB≌△CEF 所以∠B＝∠CFE 因为∠B＋∠D＝180°,∠CFE＋∠CFA＝180° 所以∠D＝∠CFA 因为AC 等分∠BAD 所以∠DAC＝∠FAC 又因为AC ＝AC 所以△ADC≌△AFC（SAS ） 所以AD ＝AF 所以AE ＝AF ＋FE ＝AD ＋BE12. 如图,四边形ABCD 中,AB ∥DC,BE.CE 分离等分∠ABC.∠BCD,且点E 在AD 上.求证：BC=AB+DC.证实:在BC 上截取BF=BA,衔接EF.∠ABE=∠FBE,BE=BE,则⊿ABE≌ΔFBE(SAS),∠EFB=∠A; AB 平行于CD,则:∠A+∠D=180°; 又∠EFB+∠EFC=180°,则∠EFC=∠D; 又∠FCE=∠DCE,CE=CE,故⊿FCE≌ΔDCE(AAS),FC=CD. 所以,BC=BF+FC=AB+CD.13.已知：AB//ED,∠EAB=∠BDE,AF=CD,EF=BC,求证：∠F=∠C D CB A FEAB//ED,AE//BD 推出AE=BD,又有AF=CD,EF=BC所以三角形AEF 全等于三角形DCB,所以:∠C=∠F14. 已知：AB=CD,∠A=∠D,求证：∠B=∠C证实：设线段AB,CD 地点的直线交于E,（当AD<BC 时,E 点是射线BA,CD 的交点,当AD>BC时,E 点是射线AB,DC 的交点）.则： △AED 是等腰三角形. 所以：AE=DE 而AB=CD 所以：BE=CE (等量加等量,或等量减等量） 所以：△BEC 是等腰三角形 所以：角B=角C.15. P 是∠BAC 等分线AD 上一点,AC>AB,求证：PC-PB<AC-AB作B 关于AD 的对称点B‘,因为AD 是角BAC 的等分线,B'在线段AC 上（在AC 中央,因为AB 较短） 因为PC<PB’+B‘C,PC -PB’<B‘C,而B'C=AC-AB'=AC-AB,所以PC-PB<AC-AB16. 已知∠ABC=3∠C,∠1=∠2,BE ⊥AE,求证：AC-AB=2BE∠BAC=180-（∠ABC+∠C=180-4∠C∠1=∠BAC/2=90-2∠C∠ABE=90-∠1=2∠C延伸BE 交AC 于F A BC D PD A C B因为,∠1 =∠2,BE⊥AE所以,△ABF 是等腰三角形 AB=AF,BF=2BE ∠FBC=∠ABC -∠ABE=3∠C -2∠C=∠C BF=C F AC-AB=AC-AF=CF=BF=2BE17. 已知,E 是AB 中点,AF=BD,BD=5,AC=7,求DC 作AG∥BD 交DE 延伸线于G AGE 全等BDE AG=BD=5 AGF∽CDFAF=AG=5所以DC=CF=218．（5分）如图,在△ABC 中,BD =DC ,∠1=∠2,求证：AD ⊥BC ．延伸AD 至H 交BC 于H; BD=DC;所以: ∠DBC=∠角DCB; ∠1=∠2;∠DBC+∠1=∠角DCB+∠2; ∠ABC=∠ACB;所以: AB=AC;三角形ABD 全等于三角形ACD;∠BAD=∠CAD; AD 是等腰三角形的顶角等分线 所以: AD 垂直BC19．（5分）如图,OM 等分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A .B 为垂足,AB 交OM 于点N ．求证：∠OAB =∠OBA因为AOM 与MOB 都为直角三角形.共用OM,且∠MOA=∠MOB F A EDCB所以MA=MB 所以∠MAB=∠MBA因为∠OAM=∠OBM=90度所以∠OAB=90-∠MAB ∠OBA=90-∠MBA 所以∠OAB=∠OBA20．（5分）如图,已知AD ∥BC ,∠PAB 的等分线与∠CBA 的等分线订交于E ,CE 的连线交AP 于D ．求证：AD +BC =AB ．证实： 做BE 的延伸线,与AP 订交于F 点, ∵PA//BC ∴∠PAB+∠CBA=180°,又∵,AE,BE 均为∠PAB 和∠CBA 的角等分线∴∠EAB+∠EBA=90°∴∠AEB=90°,EAB 为直角三角形 在三角形ABF 中,AE⊥BF,且AE 为∠FAB 的角等分线∴三角形FAB 为等腰三角形,AB=AF,BE=EF 在三角形DEF 与三角形BEC 中, ∠EBC=∠DFE,且BE=EF,∠DEF=∠CEB, ∴三角形DEF 与三角形BEC 为全等三角形,∴DF=BC ∴AB=A F=AD+DF=AD+BC21．（6分）如图,△ABC 中,AD 是∠CAB 的等分线,且AB =AC +CD ,求证：∠C =2∠B证实：在AB 上找点E,使AE=AC∵AE=AC,∠EAD=∠CAD,AD=AD∴△ADE≌△ADC.DE=CD,∠AED=∠C∵AB=AC+CD,∴DE=CD=AB -AC=AB-AE=BE∠B=∠EDB ∠C=∠B+∠EDB=2∠B22．（6分）如图①,E .F 分离为线段AC 上的两个动点,且DE ⊥AC 于E,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M ．PED C BA D C BA（1）求证：MB =MD ,ME =MF（2）当E .F 两点移动到如图②的地位时,其余前提不变,上述结论可否成立？若成立请赐与证实;若不成立请解释来由．剖析：经由过程证实两个直角三角形全等,即Rt△DEC≌Rt△BFA 以及垂线的性质得出四边形BEDF 是平行四边形．再依据平行四边形的性质得出结论．解答：解：（1）衔接BE,DF ． ∵DE⊥AC 于E,BF⊥AC 于F,, ∴∠DEC=∠BFA=90°,DE∥BF, 在Rt△DEC 和Rt△BFA 中, ∵AF=CE,AB=CD, ∴Rt△DEC≌Rt△BFA, ∴DE=BF ． ∴四边形BEDF 是平行四边形． ∴MB=MD,ME=MF;（2）衔接BE,DF ． ∵DE⊥AC 于E,BF⊥AC 于F,, ∴∠DEC=∠BFA=90°,DE∥BF, 在Rt△DEC 和Rt△BFA 中, ∵AF=CE,AB=CD, ∴Rt△DEC≌Rt△BFA, ∴DE=BF ． ∴四边形BEDF 是平行四边形． ∴MB=MD,ME=MF．23．（7分）已知：如图,DC ∥AB ,且DC =AE ,E 为AB 的中点,（1）求证：△AED ≌△EBC ．（2）不雅看图前,在不添帮助线的情形下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形．（直接写出成果,不请求证实）：(1)DC∥AE,且DC=AE,所以四边形AECD 是平行四边形.于是知AD=EC,且∠EAD=∠BEC.由AE=BE,所以△AED≌△EBC.O ED C B A（2）△AEC.△ACD.△ECD 都面积相等.24．（7分）如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的等分线,BD 的延伸线垂直于过C 点的直线于E ,直线CE 交BA 的延伸线于F ．求证：BD =2CE ． 证实：延伸BA.CE,两线订交于点 F ∵BE⊥CE ∴∠BEF=∠BEC=90° 在△BEF 和△BEC 中∠FBE=∠CBE, BE=BE, ∠BEF=∠BEC∴△BEF≌△BEC(ASA) ∴EF=EC ∴CF=2CE∵∠ABD+∠ADB=90°,∠ACF+∠CDE=90° 又∵∠ADB=∠CDE ∴∠ABD=∠ACF 在△ABD 和△ACF 中 ∠ABD=∠ACF, AB=AC, ∠BAD=∠CAF=90° ∴△ABD≌△ACF(ASA) ∴BD=CF ∴BD=2CE25.（10分）如图：DF=CE,AD=BC,∠D=∠C.求证：△AED ≌△BFC.26.（10分）如图：AE.BC 交于点M,F 点在AM 上,BE ∥CF,BE=CF.求证：AM 是△ABC 的中线.证实： ∵BE‖CF∴∠E=∠CFM,∠EBM=∠FCM ∵BE=CF∴△BEM≌△CFM∴BM=CM ∴AM 是△ABC 的中线.27.（10分）如图：在△ABC 中,BA=BC,D 是AC 的中点.求证：BD ⊥AC.FED C B AM F E CBA三角形ABD 和三角形BCD 的三条边都相等,它们全等,所以角ADB和角CDB 相等,它们的和是180度,所以都是90度,BD 垂直AC28.（10分）AB=AC,DB=DC,F 是AD 的延伸线上的一点.求证：BF=CF证实：在△ABD 与△ACD 中AB=AC BD=DCAD=AD∴△ABD≌△ACD ∴∠ADB=∠ADC∴∠BDF=∠FDC 在△BDF 与△FDC 中 BD=DC ∠BDF=∠FDC DF=DF∴△FBD≌△FCD ∴BF=FC29.（12分）如图：AB=CD,AE=DF,CE=FB.求证：AF=DE.因为AB=DC AE=DF, CE=FBCE+EF=EF+FB 所以三角形ABE=三角形CDF因为 角DCB=角ABF AB=DC BF=CE 三角形ABF=三角形CDE 所以AF=DE 30.公园里有一条“Z”字形道路ABCD ,如图所示,个中AB ∥CD ,在AB ,CD ,BC 三段路旁各有一只小石凳E ,F ,M ,且BE ＝CF ,M 在BC 的中点,试解释三只石凳E ,F ,M 正好在一条直线上.证： ∵AB 平行CD （已知） ∴∠B=∠C（两直线平行,内错角相等） ∵M 在BC 的中点（已知） ∴EM=FM（中点界说） 在△BME DCB A FD CB A F E DC BA和△CMF 中 BE=CF （已知） ∠B=∠C （已证） EM=FM （已证） ∴△BME 全等与△CMF（SAS ） ∴∠EMB=∠FMC（全等三角形的对应角相等）∴∠EMF=∠EMB+∠BMF=∠FMC+∠BMF=∠BMC=180°（等式的性质） ∴E,M,F 在统一向线上31．已知：点A.F.E.C 在统一条直线上, AF ＝CE,BE∥DF,BE＝DF ．求证：△ABE≌△CDF．证实： ∵AF=CE ∴AF+EF=CE+EF ∴AE=CF∵BE//DF ∴∠BEA=∠DFC 又∵BE=DF∴⊿ABE≌⊿CDF（SAS ）32.已知：如图所示,AB ＝AD,BC ＝DC,E.F 分离是DC.BC 的中点,求证： AE ＝AF.贯穿连接BD,得到等腰三角形ABD 和等腰三角形BDC,由等腰△两底角相等得：角ABC=角ADC 在联合已知前提证得：△ADE ≌△ABF得AE=AF 33．如图,在四边形ABCD 中,E 是AC 上的一点,∠1=∠2,∠3=∠4,求证: ∠5=∠6．因为角1=角2∠3=∠4所以角ADC=角ABC. 又因为AC 是公共边,所以AAS==>三角形ADC 全等于三角形ABC. 所以BC 等于DC,角3等于角4,EC=EC 三角形DEC 全等 DA F E 654321E D CB A于三角形BEC 所以∠5=∠634．已知AB ∥DE ,BC ∥EF ,D ,C 在AF 上,且AD ＝CF ,求证：△ABC ≌△DEF ．因为D,C 在AF 上且AD=CF 所以AC=DF 又因为AB 平行DE,BC 平行EF 所以角A+角EDF,角BCA=角F （两直线平行,内错角相等） 然后SSA （角角边）三角形全等35．已知：如图,AB =AC ,BD AC ,CE AB ,垂足分离为D .E ,BD .CE 订交于点F ,求证：BE =CD ．证实：因为 AB=AC, 所以∠EBC=∠DCB 因为 BD⊥AC,CE⊥AB 所以 ∠BEC=∠CDB BC=CB (公共边) 则有 三角形EBC 全等于三角形DCB 所以 BE ＝CD36、如图,在△ABC 中,AD 为∠BAC 的等分线,DE ⊥AB 于E ,DF ⊥AC 于F .求证：DE =DF ．AAS 证△ＡＤＥ≌△ADF37.已知：如图, AC ⊥BC 于C , DE ⊥AC 于E , AD ⊥AB 于A , BC =AE ．若AB =5 ,求AD 的长？ 角C=角E=90度 角B=角EAD=90度-角BACBC=AE A C B DE F A EDC FD C B A E△ABC ≌△DAEAD=AB=538．如图：AB=AC,ME ⊥AB,MF ⊥AC,垂足分离为E.F,ME=MF.求证：MB=MC证实∵AB=AC∴△ABC 是等腰三角形 ∴∠B=∠C又∵ME=MF,△BEM 和△CEM 是直角三角形∴△BEM 全等于△CEM ∴MB=MC39.如图,给出五个等量关系：①AD BC =②AC BD =③CE DE =④D C ∠=∠⑤DAB CBA ∠=∠．请你以个中两个为前提,另三个中的一个为结论,推出一个准确的结论（只需写出一种情形）,并加以证实．已知：求证：证实：已知1,2 求证4 因为AD=BC AC=BD,在四边形ADBC 中,连AB 所以△ADB 全等于△BCA 所以角D=角C以4,5为前提,1为结论. 即：在四边形ABCD 中,∠D=∠C,∠A=∠B,求证：AD=BC 因为 ∠A+∠B+∠C+∠D=360∠D=∠C,∠A=∠B, 所以 2(∠A+∠D)=360°, ∠A+∠D=180°, 所以 AB//DC40．在△ABC 中,︒=∠90ACB ,BC AC =,直线MN 经由点C ,且C A B CＤ ＥMN AD ⊥于D ,MN BE ⊥于E .(1)当直线MN 绕点C 扭转到图1的地位时,求证： ①ADC ∆≌CEB ∆;②BE AD DE +=;(2)当直线MN 绕点C 扭转到图2的地位时,（1）中的结论还成立吗？若成立,请给出证实;若不成立,解释来由.（1）证实：∵∠ACB=90°, ∴∠ACD+∠BCE=90°, 而AD⊥MN 于D,BE⊥MN 于E, ∴∠ADC=∠CEB=90°,∠BCE+∠CBE=90°, ∴∠ACD=∠CBE． 在Rt△ADC 和Rt△CEB中,{∠ADC=∠CEB∠ACD=∠CBE AC=CB, ∴Rt△ADC≌Rt△CEB （AAS ）, ∴AD=CE,DC=BE, ∴DE=DC+CE=BE+AD;（2）不成立,证实：在△ADC 和△CEB中,{∠ADC=∠CEB=90°∠ACD=∠CBE AC=CB, ∴△ADC≌△CEB （AAS ）, ∴AD=CE,DC=BE, ∴DE=CE -CD=AD-BE;41．如图所示,已知AE ⊥AB,AF ⊥AC,AE=AB,AF=AC.求证：（1）EC=BF;（2）EC ⊥BF（1）证实;因为AE 垂直AB 所以角EAB=角EAC+角CAB=90度 因为AF 垂直AC 所以角CAF=角CAB+角BAF=90度 所以角EAC=角BAF 因为AE=AB AF=AC 所以三角形EAC和三角形FAB 全等 所以EC=BF 角ECA=角F（2）(2)延伸FB 与EC 的延伸线交于点G 因为角ECA=角F(已证） 所以角G=角CAF 因为角CAF=90度 所以EC 垂直BF42．如图：BE ⊥AC,CF ⊥AB,BM=AC,CN=AB.求证：（1）AM=AN;A E B M C F（2）AM ⊥AN.证实： （1） ∵BE⊥AC,CF⊥AB ∴∠ABM+∠BAC=90°,∠ACN+∠BAC=90° ∴∠ABM=∠ACN ∵BM=AC,CN=AB ∴△ABM≌△NAC ∴AM=AN（2） ∵△ABM≌△NAC ∴∠BAM=∠N ∵∠N+∠BAN=90° ∴∠BAM+∠BAN=90° 即∠MAN=90° ∴AM⊥AN43．如图,已知∠A=∠D,AB=DE,AF=CD,BC=EF.求证:BC ∥EF 衔接BF.CE,证实△ABF 全等于△DEC（SAS ）,然后经由过程四边形BCEF 对边相等的证得平行四边形BCEF从而求得BC 平行于EF44．如图,已知AC ∥BD,EA.EB 分离等分∠CAB 和∠DBA,CD 过点E,则AB 与AC+BD 相等吗？请解释来由在AB 上取点N ,使得AN=AC∠CAE=∠EAN ,AE 为公共边,所以三角形CAE 全等三角形EAN所以∠ANE=∠ACE 又AC 平行BD所以∠ACE+∠BDE=180 而∠ANE+∠ENB=180所以∠ENB=∠BDE ∠NBE=∠EBN BE 为公共边,所以三角形EBN 全等三角形EBD F C AM N E1234所以BD=BN 所以AB=AN+BN=AC+BD45.（10分） 如图,已知: AD 是BC 上的中线 ,且DF=DE ．求证:BE ∥CF ．证实： ∵AD 是中线 ∴BD=CD∵DF=DE,∠BDE=∠CDF ∴△BDE≌△CDF∴∠BED=∠CFD ∴BE‖CF46.(10分)已知：如图,AB ＝CD ,DE ⊥AC ,BF⊥AC ,E ,F 是垂足,DE BF ．求证：AB CD ∥．证实：∵DE⊥AC,BF⊥AC,∴∠DEC=∠AFB=90°, 在Rt△DEC 和Rt△BFA 中,DE=BF,AB=CD, ∴Rt△DEC≌Rt△BFA, ∴∠C=∠A, ∴AB∥CD．47.(10分)如图,已知∠1=∠2,∠3=∠4,求证：AB=CD【待定】48.(10分)如图,已知AC ⊥AB,DB ⊥AB,AC ＝BE,AE ＝BD,试猜测线段CE 与DE 的大小与地位关系,并证实你的结论.结论：CE>DE.当∠AEB 越小,则DE 越小. 证实： 过D 作AE 平行线与AC 交于F,衔接FB 由已知前提知AFDE 为平行四边形,ABEC 为矩形 ,且△DFB 为等腰三角形. RT△BAE 中,∠AEB 为锐角,即∠AEB<90° AC E DB A D EC B F∵DF//AE ∴∠FDB=∠AEB<90° △DFB 中∠DFB=∠DBF=(180°-∠FDB)/2>45° RT△AFB 中,∠FBA=90°-∠DBF <45° ∠AFB=90°-∠FBA>45° ∴AB>AF ∵AB=CE AF=DE ∴CE>DE49.(10分)如图,已知AB ＝DC,AC ＝DB,BE ＝CE,求证：AE ＝DE. 先证实△ABC ≌△BDC 的出角ABC=角DCB 在证实△ABE ≌△DCE得出AE=DE 50．如图9所示,△ABC 是等腰直角三角形,∠ACB ＝90°,AD 是BC 边上的中线,过C 作AD 的垂线,交AB 于点E,交AD 于点F,求证：∠ADC ＝∠BDE ．证实：作CG 等分∠ACB 交AD 于G∵∠ACB=90° ∴∠ACG= ∠DCG=45°∵∠ACB=90° AC=BC ∴∠B=∠BAC=45° ∴∠B=∠DCG=∠ACG ∵CF⊥AD ∴∠ACF+∠DCF=90° ∵∠ACF+∠CAF=90°∴∠CAF=∠DCF ∵ AC=CB ∠ACG=∠B ∴△ACG≌△CBE ∴CG=BE ∵∠DCG=∠B CD=BD ∴△CDG ≌△BDE ∴∠ADC=∠BDE AB EC DA B C D E F 图9。

全等三角形证明经典50题（含答案）1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。

因为 BC=ED,CF=DF,∠BCF=∠EDF 。

所以 三角形BCF 全等于三角形EDF(边角边)。

所以 BF=EF,∠CBF=∠DEF 。

连接BE 。

在三角形BEF 中,BF=EF 。

所以 ∠EBF=∠BEF 。

又因为 ∠ABC=∠AED 。

所以 ∠ABE=∠AEB 。

所以 AB=AE 。

在三角形ABF 和三角形AEF 中， AB=AE,BF=EF, ∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。

所以 三角形ABF 和三角形AEF 全等。

所以 ∠BAF=∠EAF (∠1=∠2)。

ADBC4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC证明： 过E 点，作EG//AC ，交AD 延长线于G 则∠DEG=∠DCA ，∠DGE=∠2 又∵CD=DE ∴⊿ADC ≌⊿GDE （AAS ） ∴EG=AC ∵EF//AB ∴∠DFE=∠1 ∵∠1=∠2 ∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C证明： 在AC 上截取AE=AB ，连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ，AD=AD ∴⊿AED ≌⊿ABD （SAS ） ∴∠AED=∠B ，DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE证明： 在AE 上取F ，使EF ＝EB ，连接CF 因为CE ⊥AB 所以∠CEB ＝∠CEF ＝90° 因为EB ＝EF ，CE ＝CE ， 所以△CEB ≌△CEF 所以∠B ＝∠CFE 因为∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180° 所以∠D ＝∠CFA 因为AC 平分∠BAD 所以∠DAC ＝∠FAC 又因为AC ＝AC 所以△ADC ≌△AFC （SAS ） 所以AD ＝AF 所以AE ＝AF ＋FE ＝AD ＋BE12. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

全等三角形证明经典50题（含答案）1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。

因为 BC=ED,CF=DF,∠BCF=∠EDF 。

所以 三角形BCF全等于三角形EDF(边角边)。

所以 BF=EF,∠CBF=∠DEF 。

连接BE 。

在三角形BEF 中,BF=EF 。

所以 ∠EBF=∠BEF 。

又因为 ∠ABC=∠AED 。

所以 ∠ABE=∠AEB 。

所以 AB=AE 。

在三角形ABF 和三角形AEF 中，AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。

所以 三角形ABF 和三角形AEF 全等。

所以 ∠BAF=∠EAF (∠1=∠2)。

ADBC4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC 证明：过E 点，作EG//AC ，交AD 延长线于G 则∠DEG=∠DCA ，∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE （AAS ）∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC 5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C证明：在AC 上截取AE=AB ，连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ，AD=AD ∴⊿AED ≌⊿ABD （SAS ）∴∠AED=∠B ，DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C 6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE证明： 在AE 上取F ，使EF ＝EB ，连接CF 因为CE ⊥AB 所以∠CEB ＝∠CEF ＝90° 因为EB ＝EF ，CE ＝CE ， 所以△CEB ≌△CEF 所以∠B ＝∠CFE 因为∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180° 所以∠D ＝∠CFA 因为AC 平分∠BAD 所以∠DAC ＝∠FAC 又因为AC ＝AC 所以△ADC ≌△AFC （SAS ） 所以AD ＝AF 所以AE ＝AF ＋FE ＝AD ＋BE 12. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

全等三角形证明经典50题（含答案）1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB —BE 〈AE<AB+BE 即：10-2<2AD<10+2 4〈AD 〈6 又AD 是整数，则AD=52. 已知：D 是AB 中点,∠ACB=90°，求证：12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点,求证:∠1=∠2证明：连接BF 和EF 。

因为 BC=ED ，CF=DF ，∠BCF=∠EDF 。

所以 三角形BCF 全等于三角形EDF(边角边）.所以 BF=EF,∠CBF=∠DEF 。

连接BE.在三角形BEF 中，BF=EF.所以 ∠EBF=∠BEF 。

又因为 ∠ABC=∠AED.所以 ∠ABE=∠AEB 。

所以 AB=AE 。

在三角形ABF 和三角形AEF 中，AB=AE ，BF=EF ，∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。

所以 三角形ABF 和三角形AEF 全等。

所以 ∠BAF=∠EAF (∠1=∠2）。

ADBC4. 已知:∠1=∠2，CD=DE ，EF//AB ，求证:EF=AC 证明：过E 点，作EG//AC,交AD 延长线于G 则∠DEG=∠DCA ，∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE （AAS ）∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知：AD 平分∠BAC,AC=AB+BD ，求证:∠B=2∠C证明：在AC 上截取AE=AB ，连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB,AD=AD ∴⊿AED ≌⊿A BD （SAS ）∴∠AED=∠B ，DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE ∴∠C=∠ED C ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证:AE=AD+BE证明： 在AE 上取F ，使EF ＝EB ，连接CF 因为CE ⊥AB 所以∠CEB＝∠CEF ＝90° 因为EB ＝EF ，CE ＝CE ， 所以△CEB ≌△CEF 所以∠B ＝∠CFE 因为∠B ＋∠D ＝180°,∠CFE ＋∠CFA ＝180° 所以∠D ＝∠CFA 因为AC 平分∠BAD 所以∠DAC ＝∠FAC 又因为AC ＝AC 所以△ADC ≌△AFC(SAS ） 所以AD ＝AF 所以AE ＝AF ＋FE ＝AD ＋BE12。

1一，证明边或角相等方法：证明两条线段相等或角相等，如果这两条线段或角在两个三角形内，就证明这两个三角形全等；如果这两条线段或角在同一个三角形内，就证明这个三角形是等腰三角形；如果看图时两条线段既不在同一个三角形内，也不在两个全等三角形内，那么就利用辅助线进行等量代换，同样如果角不在同一个三角形内，也不在两个全等三角形内，也是用等量代换（方法是：（1）同角（等角）的余角相等（2）同角（等角）的补角相等，此类型问题一般不单独作一大题，往往是通过得出角相等后用来证明三角形全等，而且一般是在双垂直的图形中）1.已知，如图，AB ⊥AC ，AB ＝AC ，AD ⊥AE ，AD ＝AE 。

求证：BE ＝CD 。

2．如图，在四边形ABCD 中，E 是AC 上的一点，∠1=∠2，∠3=∠4，求证: ∠5=∠6．3．已知：如图△ABC 中，AB=AC ，BD ⊥AC ，CE ⊥AB ，BD 、CE 交于H 。

求证：HB=HC 。

2、如图, 已知：AB ⊥BC 于B , EF ⊥AC 于G , DF ⊥BC 于D , BC=DF ．求证：AC=EF ．A ED C B654321E DCBAFGE D CBAFMNE 1234134****70432EDC BA 二.证明线段和差问题 （形如：AB+BC=CD,AB=AD - CD)证明两条线段和等于另一条线段，常常使用截长补短法。

①截长法即为在这三条最长的线段截取一段使它等于较短线段中的一条，然后证明剩下的一段等于另一条较短的线段。

②补短法即为在较短的一条线段上延长一段，使它们等于最长的线段，然后证明延长的这一线段等于另一条较短的线段。

证明两条线段差等于另一条线段，只需把差化成和来解决即可。

1.如图，已知AD ∥BC ，∠PAB 的平分线与∠CBA 的平分线相交于E ，CE 的连线交AP 于D ．求证：AD +BC =AB ．2、如图,已知：△ABC 中,∠BAC ＝90, AB ＝AC ,AE 是过A 一直线,且点B 、C 在AE 的异侧,BD ⊥AE 于D ,CE ⊥AE 于E . 求证：BD ＝DE ＋CE ；3、如图，AB ∥CD ，DE 平分∠ADC ，AE 平分∠BAD ，求证：AB=AD - CD三．证明线段的2倍或21关系 ( AB CE =2， MN BN =12） P E D CB A134****704331. 利用含30角的直角三角形的性质证明例1. 已知，如图1，∆ABC 是等边三角形，在AC 、BC 上分别取点D 、E ，且AD ＝CE ，连结AE 、BD 交于点N ，过B 作BM AE ⊥，垂足为M ，求证：MN BN =12（提示：先证∠=BNE 60）2. 利用等线段代换（充分利用中点）例1．如图，△ABC 中，∠BAC =90度，AB =AC ，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E ，直线CE 交BA 的延长线于F ． 求证：BD =2CE ．3.转化为线段和问题，利用截长补短法例5. 已知：如图5，四边形ABCD 中，∠=D 90，对角线AC 平分∠BAD ，AC BC =，求证：AD AB =12四．证明二倍角关系利用三角形外角和定理和等量代换如图，△ABC 中，AD 是∠CAB 的平分线，且AB =AC +CD ，求证：∠C =2∠B FE DCB ADCBA134****7043 4。

全等三角形证明经典50题（含答案）1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD /即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2 ~证明：连接BF 和EF 。

因为 BC=ED,CF=DF,∠BCF=∠EDF 。

所以 三角形BCF 全等于三角形EDF(边角边)。

所以 BF=EF,∠CBF=∠DEF 。

连接BE 。

在三角形BEF 中,BF=EF 。

所以 ∠EBF=∠BEF 。

又因为 ∠ABC=∠AED 。

所以 ∠ABE=∠AEB 。

所以 AB=AE 。

在三角形ABF 和三角形AEF 中，AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。

所以 三角形ABF 和三角形AEF 全等。

所以 ∠BAF=∠EAF (∠1=∠2)。

BADBCC(4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC证明：过E 点，作EG//AC ，交AD 延长线于G 则∠DEG=∠DCA ，∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE （AAS ）∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C证明：在AC 上截取AE=AB ，连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ，AD=AD ∴⊿AED ≌⊿ABD （SAS ）∴∠AED=∠B ，DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE证明： 在AE 上取F ，使EF ＝EB ，连接CF 因为CE ⊥AB 所以∠CEB ＝∠CEF ＝90° 因为EB ＝EF ，CE ＝CE ， 所以△CEB ≌△CEF 所以∠B ＝∠CFE 因为∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180° 所以∠D ＝∠CFA 因为AC 平分∠BAD 所以∠DAC ＝∠FAC 又因为AC ＝AC 所以△ADC ≌△AFC （SAS ） 所以AD ＝AF 所以AE ＝AF ＋FE ＝AD ＋BE12. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD2. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠24. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=ACADBCBA CDF2 1 E5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE7. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD8. 已知：D 是AB 中点，∠ACB=90°，求证：12CD ABADB CCDB A9. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠210. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC11. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C12. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BEBA CDF2 1 ECDB A12. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

求证：BC=AB+DC 。

13.已知：AB//ED ，∠EAB=∠BDE ，AF=CD ，EF=BC ，求证：∠F=∠C14. 已知：AB=CD ，∠A=∠D ，求证：∠B=∠CDCBAFEAB C D15. P 是∠BAC 平分线AD 上一点，AC>AB ，求证：PC-PB<AC-AB16. 已知∠ABC=3∠C ，∠1=∠2，BE ⊥AE ，求证：AC-AB=2BE17. 已知，E 是AB 中点，AF=BD ，BD=5，AC=7，求DC18．（5分）如图，在△ABC 中，BD =DC ，∠1=∠2，求证：AD ⊥BC ． 19．（5分）如图，OM 平分∠POQ ，MA ⊥OP ,MB ⊥OQ ，A 、B 为垂足，AB 交OM 于点N ．求证：∠OAB =∠OBAP D ACBFAED C B20．（5分）如图，已知AD ∥BC ，∠P AB 的平分线与∠CBA 的平分线相交于E ，CE 的连线交AP 于D ．求证：AD +BC =AB ．21．（6分）如图，△ABC 中，AD 是∠CAB 的平分线，且AB =AC +CD ，求证：∠C =2∠B22．（6分）如图①，E 、F 分别为线段AC 上的两个动点，且DE ⊥AC 于E ，BF ⊥AC 于F ，若AB =CD ，AF =CE ，BD 交AC 于点M ． （1）求证：MB =MD ，ME =MF（2）当E 、F 两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由．23．（7分）已知：如图，DC ∥AB ，且DC =AE ，E 为AB 的中点， （1）求证：△AED ≌△EBC ．P EDCBA D CBA（2）观看图前，在不添辅助线的情况下，除△EBC 外，请再写出两个与△AED 的面积相等的三角形．（直接写出结果，不要求证明）：24．（7分）如图，△ABC 中，∠BAC =90度，AB =AC ，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E ，直线CE 交BA 的延长线于F ． 求证：BD =2CE ．25、（10分）如图：DF=CE ，AD=BC ，∠D=∠C 。