八年级数学中心对称图形1
- 格式:ppt
- 大小:800.00 KB
- 文档页数:29

八年级数学(上)第三章中心对称图形(一)(附答案)第2课时中心对称与中心对称图形(一)1.把一个图形绕着某一点旋转180°,如果它能够与另外一个图形重合,那么称这两个图形关于这点对称,也称这两个图形成________,这个点叫做_______,_______叫做对称点.2.成中心对称的两个图形__________________________________________.3.如图,两个三角形成中心对称,请确定其对称中心.4.分别画出下列各图关于点O成中心对称的图形.5.下图是由两个半圆组成,点B是AC的中点,画出此图形关于点B成中心对称的图形.6.若两个图形关于某一点成中心对称,则下列说法:①这两个图形一定全等;②对称点的连线一定经过对称中心;③将一个图形绕对称中心旋转某个定角必定与另一个图形重合;④一定存在某直线,沿该直线折叠后的两个图形互相重合.其中,正确的是________(填序号).7.如图,在四边形ABCD中,AD∥BC,E是CD的中点.(1)画图:连接AE并延长,交BC的延长线于点F,连接BE;(2)填空:点A与点F关于点________对称,△ADE与_______关于点______成中心对称.若AB=AD+BC,则△ABF是_________三角形,BE是线段AF的_________线;(3)作图后,图中△_________的面积等于四边形ABCD的面积.8.如图,线段AB与点O的位置关系如图所示,试画出线段AB关于点O对称的线段A′B′.9.分别画出下图中与△ABC关于点O成中心对称的三角形A′B′C′.10.如图,两个能重合的长方形关于某一点成中心对称,请画出其对称中心.11.如图,D是△ABC边BC的中点,连接AD并延长,使DE=AD,连接BE.(1)图中哪两个图形成中心对称?(2)若△ADC的面积为4,求△ABE的面积.参考答案1.中心对称对称中心两个图形的对应点2.对称点的连线都经过对称中心,并且被对称中心平分3.略4.略5.略6.①②③7.(1)略(2)E △FCE E等腰垂直平分(3)ABF 8.略9.略10.略11.(1)△ACD与△EBD (2)8。

八年级数学(上)第三章中心对称图形(一)第10课时矩形、菱形、正方形(3)(附答案)1.菱形除了具有平行四边形的性质外,还有一些特殊的性质:四条边__________,对角线_________,并且________________.2.已知菱形的周长为16 cm,则它的边长为___________cm.3.菱形的一组邻角之比为1:2,较短的对角线为5 cm,则此菱形的周长为__________.4.边长为5 cm的菱形,它的一条对角线长6 cm,则另一条对角线长_______.5.已知菱形的两条对角线长分别是30 cm和40 cm,则它的面积为_________cm2.6.如图,在菱形ABCD中,点E、F分别是BC、CD的中点,连接AE、AF.你能说明AE 与AF的关系吗?为什么?7.如图,四边形ABCD是菱形,DE⊥AB,交BA的延长线于点E,DF⊥BC,交BC的延长线于点F.请你猜想DE与DF的大小有什么关系?并证明你的猜想.8.如图,在菱形ABCD中,∠A=60°,BD=6 cm,则△BCD是_________三角形,菱形ABCD的周长为__________cm.9.如图,P为菱形ABCD的对角线上一点,PE⊥AB于点E,PF⊥D于点F,PF=3 cm;则P点到AB的距离是_________cm.10.菱形具有而矩形不一定具有的特征是( ) A.对角线相等B.四个内角相等C.对角线互相平分D.对角线互相垂直11.如图,在菱形ABCD中,∠B=60°,AB=2,E、F分别是BC、CD 的中点,连接AE、EF、AF,则△AEF的周长为( )A.B.C.D.312.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为( )A.1 B.2 C D13.如图,在□ABCD中,BC=2AB=4,点E、F分别是BC、AD的中点.(1)试说明△ABE≌△C'DF.(2)当四边形AECF为菱形时,求出该菱形的面积.14.如图,菱形ABCD的对角线AC、BD相交于点O,AC=8 cm,BD=6 cm.求菱形的高DH的长.15.如图,在菱形.ABCD中,∠A=72°,请设计三种不同的分法,将菱形ABCD分割成四个三角形,使得每个三角形都是等腰三角形(画图工具不限,要求画出分割线段,求出每种分法所得三角形内角的度数,只要有一条分割线段位置不同,就认为是两种不同的分法).参考答案1.相等互相垂直平分一组对角2.43.20 cm4.8 cm5.6006.AE=AF7.DE=DF 连接BD,则DB平分∠ABC.∵DF⊥BC,DE⊥AB.∴DE=DF 8.等边249.310.D 11.B 12.D13.(1)略(2)14.4.8 cm15.如图,只要画出其中任意三种即可。


中心对称图形1、中心对称:如果把一个图形绕一个点旋转180°后能够与另一个图形完全重合,那么这两个图形关于这点成中心对称。
2、中心对称图形:把一个图形绕一个点旋转180°后能够与自身完全重合,那么这个图形是中心对称图形。
3、中心对称的性质:①关于中心对称的两个图形是全等的。
②关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分。
4、真命题:如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点成中心对称。
5、平行四边形的定义:两组对边分别平行的四边形叫作平行四边形。
6、平行四边形性质:①平行四边形的对角相等。
②平行四边形的对边相等。
③平行四边形的对角线互相平分。
7、平行四边形判定:①两组对边分别相等的四边形是平行四边形。
②对角线互相平分的四边形是平行四边形。
③一组对边平行且相等的四边形是平行四边形。
④真命题:两组对角分别相等的四边形是平行四边形。
⑤真命题:一组对边平行,一组对角相等的四边形是平行四边形。
注意:假命题...:一组对边相等,一组对角相等的四边形是平行四边形。
(×)8、矩形的定义:有一个角是直角的平行四边形叫作矩形。
9、矩形的性质:①矩形的四个角都是直角。
②矩形的对角线相等。
10、矩形的判定:①有三个角是直角的四边形是矩形。
②对角线相等的平行四边形是矩形。
11、菱形的定义:有一组邻边相等的平行四边形叫作菱形。
12、菱形的性质:①菱形的四条边都相等。
②菱形的对角线互相垂直,并且每一条对角线平分一组对角。
13、菱形面积等于对角线乘积的一半。
推而广之:(真命题)对角线互相垂直的四边形的面积等于对角线乘积的一半。
14、菱形的判定:①四边都相等的四边形是菱形。
②对角线互相垂直的平行四边形是菱形。
③真命题:一条对角线平分一个内角的平行四边形是菱形。
15、正方形的定义:有一个角是直角,并且有一组邻边相等的平行四边形叫作正方形。
16、正方形性质:正方形的四个角都是直角,四条边都相等,正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角。

八年级数学(上)第三章中心对称图形(一)第3课时中心对称与中心对称图形(二)(附答案)1.下列图形中,既是轴对称图形又是中心对称图形的是( )2.下列四张扑克牌的牌面,不是中心对称图形的是( )3.观察下列银行标志,从图案看是中心对称图形的有( )A.1个B.2个C.3个D.4个4.下列四组图形中,中心对称的图形有( ) A.1组B.2组C.3组D.4组5.如图①所示的四张牌,若将其中一张牌旋转180°后得到图②,则旋转的牌是( )6.如图,下列图形:(1)是轴对称图形的是___________,它们的对称轴分别有______________条.(2)通过旋转能完全重合的图形是_________.请在图中标出各自的旋转中心,它们分别至少旋转___________才能与原图形重合.(3)是中心对称图形的是___________.7.找出下列各图中的旋转中心,说出至少旋转多少度能与原图形重合,并说出它们是不是中心对称图形.8.如图,AC与BD互相平分且相交于点O,点E、F分别在AB、CD上,且AE=CF.试利用“中心对称”的有关知识说明:点E、O、F在同一直线上,且OE=OF.9.如图是4×4的正方形网格,请在其中选取一个白色的正方形并涂上阴影,使图中阴影部分是一个中心对称图形.10.如图,在△ABC中,D是AB边的中点,AC=4,BC=6.(1)作出△CDB关于点D的中心对称图形.(2)利用“中心对称”的有关知识,求CD的取值范围.11.如图,点M、N分别是△ABC的边BC、AC的中点,点P是点A关于点M的对称点,点Q是点B关于点N的对称点.试说明P、C、Q三点在同一条直线上.12.按要求作图.(1)如图①是有5个大小相同的圆构成的图形,若想要画一条直线把它们分割成面积相等的两个部分,该如何画?(2)如图②是一块方角形钢板,请用一条直线将其分成面积相等的两部分.参考答案1.D 2.D 3.C 4.C 5.A6.(1)①②③④4、3、6、4 (2)①②③④画图略90°,120°,60°,90°(3)①③④7.略8.略9.略10.(1)如图所示(2)B、C点的对应点为点A、E,由中心对称的特征得CD=DE,BC=AE,在△EAC中,AC+AE>CE,AE-AC<CE.∵AC=4,AE=BC=6,∴2<CE<10.∴1<CD<511.连接PC、CQ.∵点M、N分别是△ABC的边BC、AC的中点,∴BM=CM,AN=CN.∴点C是点B关于点M的对称点,点C也是点A关于点N的对称点.又∵点P是A点关于点M的对称点,点Q是点B关于点N的对称点,∴△PCM是△ABM关于点M的对称三角形,△QCN是△BAN关于点N的对称三角形.∴∠ABM=∠PCM,∠BAN=∠QCN.∴∠PCM+∠ACB+∠QCN=∠ABM+∠ACB+∠BAM=180°.∴P、C、Q三点在同一条直线上12.(1)如图①,画辅助圆,设圆心为O6,圆O2与圆O5的公共点为点O,直线O1O6过点O,显然点O为下图的对称中心,这条直线把六个圆分成面积相等的两部分,也把圆O6分成面积相等的两部分.因此,直线O1O6即为所求直线(2)中心对称图形有一个性质:过中心对称图形的对称中心的每一条直线,都将这个中心对称图形分成面积相等的两部分.图中方角形钢板虽不是中心对称图形,但可采用“割”或“补”的方法将其分成两个中心对称的图形.共有三种解法,如图②、③、④所示。
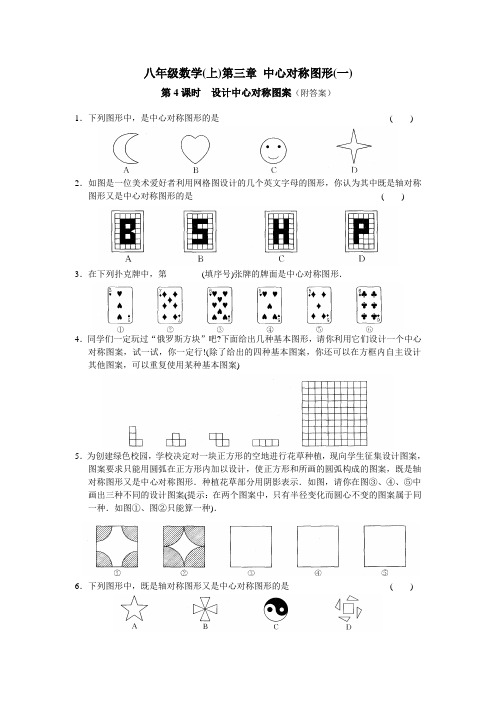
八年级数学(上)第三章中心对称图形(一)第4课时设计中心对称图案(附答案)1.下列图形中,是中心对称图形的是( )2.如图是一位美术爱好者利用网格图设计的几个英文字母的图形,你认为其中既是轴对称图形又是中心对称图形的是( )3.在下列扑克牌中,第________(填序号)张牌的牌面是中心对称图形.4.同学们一定玩过“俄罗斯方块”吧?下面给出几种基本图形,请你利用它们设计一个中心对称图案,试一试,你一定行!(除了给出的四种基本图案,你还可以在方框内自主设计其他图案,可以重复使用某种基本图案)5.为创建绿色校园,学校决定对一块正方形的空地进行花草种植,现向学生征集设计图案,图案要求只能用圆弧在正方形内加以设计,使正方形和所画的圆弧构成的图案,既是轴对称图形又是中心对称图形.种植花草部分用阴影表示.如图,请你在图③、④、⑤中画出三种不同的设计图案(提示:在两个图案中,只有半径变化而圆心不变的图案属于同一种.如图①、图②只能算一种).6.下列图形中,既是轴对称图形又是中心对称图形的是( )7.如图①,三张扑克牌放在桌子上,小敏把其中一张牌旋转180°后,如图②所示,则她所旋转的牌从左数起是( )A.第一张B.第二张C.第三张D.无法确定8.如图,方格纸中左边图形到右边图形的变换是( )A.向右平移7格B.以AB的垂直平分线为对称轴作轴对称,再以AB为对称轴作轴对称C.绕AB的中点旋转180°,再以AB为对称轴作轴对称D.以AB为对称轴作轴对称,再向右平移7格9.如图是一个中心对称图形的一半,请补出图形的另一半.10.下列网格中,各个小正方形的边长都为1,请你将最左边网格中的图形按以下要求进行分割后重新拼接,并分别画在从左至右的网格中.(1)拼得的图形是轴对称图形而不是中心对称图形.(2)拼得的图形是中心对称图形而不是轴对称图形.(3)拼得的图形既是轴对称图形又是中心对称图形.11.认真观察图①的四个图形中阴影部分构成的图案,回答下列问题:(1)请写出这四个图案都具有的两个共同特征.特征1:__________________________________________.特征2:__________________________________________.(2)请在图②中设计出你心中最美丽的图案,使它也具备你所写出的上述特征.参考答案1.D 2.C 3.⑤4.略5.略6.B 7.A 8.D 9.略10.略11.略。
八年级数学(上)第三章中心对称图形(一)第8课时矩形、菱形、正方形(一)(附答案)1.矩形除了具有平行四边形的性质外,还有一些特殊的性质:四个角是____________,对角线____________.2.如图,在矩形ABCD中,对角线AC、BD相交于点O.若∠AOB=60°,AB=4 cm,则AC的长为__________cm.3.如图,在矩形ABCD中,AB=2,BC=3,对角线AC的垂直平分线分别交AD、BC于点E、F,连接CE,则CE的长为___________.4.如图,在矩形ABCD中,E是AD上的一点,F是AB 上的一点,E F⊥EC,且EF=EC,DE=4 cm,矩形ABCD的周长为32 cm.求AE的长.5.如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连接AE.试说明:(1)BF=DF.(2)AE∥BD.6.矩形具有而一般平行四边形不具有的性质是( )A.对角相等B.对边相等C.对角线相等D.对角线互相平分7.如图,把矩形ABCD沿EF对折后使两部分重合.若∠1=50°,则∠AEF的度数为( )A.110°B.115°C.120°D.130°8.如图,四边形ABCD是矩形,AB=10 cm,∠DAC:∠BAC=1:2,则BD=_________cm,△OCD的周长为___________cm.9.如图,矩形ABCD 的两条对角线相交于点O ,过点O 作AC 的垂线EF ,分别交AD 、BC 于点E 、F ,连接CE .若△CDE 的周长为24 cm ,则矩形ABCD 的周长是________cm .10.如图,在矩形ABCD 中,AB=8 cm ,CB=4 cm ,E 是DC 的中点,BF=14BC , 则四边形DBFE 的面积为__________.11.如图,在矩形ABCD 中,AB=2,点E 在BC 上,且AE=EC .若将纸片沿AE 折叠,点B 恰好落在AC 上,则AC 的长是_________.12.如图,在△ABC 中,AB=AC ,AD ⊥BC 于点D ,AE 是∠BAC 的外角平分线,四边形ADCE 是矩形.试说明AB ∥DE .13.如图,在矩形ABCD 中,点E 是BC 上一点,AE=AD ,DF ⊥AE 于点F ,连接DE .试说明DF=DC .14.如图①,矩形ABCD 的对角线AC 、BD 相交于点O .(1)线段BO 与对角线AC 有怎样的数量关系?(2)如图②,如果去掉AD 、OD 、CD 三条线段,这时BO 便成为Rt △ABC 斜边上的什么线?由第(1)题你能得出什么结论?参考答案1.直角 相等 2.8 3.1364.在Rt △AEF 和Rt △DCE 中,∵EF ⊥CE ,∴∠FEC=90°.∴∠AEF+∠DEC=90°.又∵∠DCE+∠DEC=90°.∴∠AEF=∠DCE .又∵∠FAE=∠EDC=90°,EF=CE ,∴Rt △AEF ≌Rt △DCE .AE=CD ,AD=AE+4.∵矩形ABCD 的周长为32 cm ,∴2(AE+AE+4)=32.解得AE=6 cm 5.(1)点拨:由矩形ABCD 得∠ADB=∠EBD(或△ABF ≌△EDF),∴BF=DF (2)点拨:∠AEB=∠DBE(或∠EAD=∠BDA),∴AE ∥BD . 6.C 7.B 8.20 30 9.48 10.10cm 2 11.4 12.∵AB=AC 且 A D ⊥BC ,∴BD=DC ,∠ADC=90°.∵矩形ADCE ,∴AE ∥CD ,且AE=CD .∵B 、D 、C 在同一直线上.∴AE ∥BD ,且AE=BD .∴四边形ABDE 是平行四边形.∴AB ∥DE13.由AE=AD 得∠ADE=∠AED .又由AD ∥BC 得∠ADE=∠DEC .∴∠DEC=∠AED .∵D F ⊥AE ,∠C=90°,∴DF=DC 14.(1)BO=12BD=12AC ,即BO=12AC (2)BO 是直角△ABC 斜边上的中线 结论:直角三角形斜边上的中线等于斜边的一半。
第 1 页 共 3 页 3.2中心对称与中心对称图形(1)-- [ 教案]班级 姓名 学号学习目标经历观察.操作.分析等数学活动过程,通过具体实例认识中心对称,知道中心对称的性质.学习难点⒈中心对称的性质.⒉成中心对称的图形的画法教学过程一、情境引入利用课本提供的两个实物图,引导学生观察、探索:他们的形状、大小是否相同?如果将其中一个图形绕着某一点旋转1800,能与另一个重合吗?【设计说明:通过现实情境激发学生的好奇心和主动学习的欲望。
】二、新课讲授⒈ 引出概念:如果把一个图形绕着某一点旋转180度后能与另一个图形重合,那么我们就说,这两个图形成中心对称,这个点叫做对称中心,两个图形中的对应点叫做对称点说一说:观察你生活的周围各处,指出几个中心对称的现象,并加以数学描述。
【设计说明:通过对生活中的中心对称现象的描述,加深了对中心对称的理解,锻练了用数学语言进行表达的能力】⒉ 探索活动活动一 用一张透明纸覆盖在图3-5上,描出四边形ABCD 。
用大头针钉在点O 处,将四边形ABCD 绕点O 旋转180度问题一:四边形ABCD 与四边形A 'B 'C 'D '关于点O 成中心对称吗?问题二:在图3-5中,分别连接关于点O 的对称点A 和A '、B 和B '、C 和C '、D 和D '。
你发现了什么?【设计说明:让学生在操作与观察的基础上,发现中心对称的两个图形具有(一般地)旋转的一切性质,且具有特殊的性质——对称点连线经过对称中心,且成中心对称的2个图形,对称点的连线都经过对称中心,并且被对称中心平分第 2 页 共 3 页 被对称中心平分】活动二 中心对称与轴对称进行类比【设计说明:中心对称与轴对称都是指两个图形按某种规则运动能互相重合的特殊位置关系,教学中,将他们进行类比,进一步加深对中心对称的理解】练一练 课本98页练习1【设计说明:学习概念后,把概念直接运用到题目中,这是一个从一般到特殊的过程,也是数学学习的一大特点。