反常积分(广义积分)

反常积分的概念
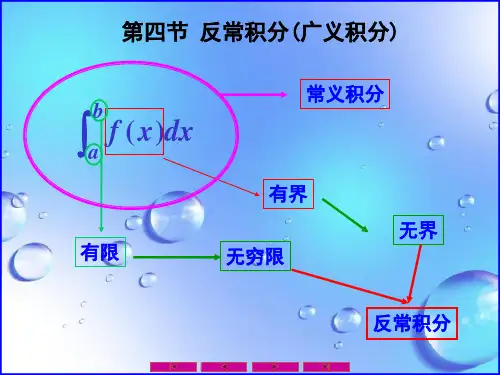
反常积分又叫广义积分，是对普通定积分的推广，指含有无穷上限/下限，或者被积函数含有瑕点的积分，前者称为无穷限广义积分，后者称为瑕积分（又称无界函数的反常积分）。

几何意义：
反常积分存在时的几何意义：函数与X轴所围面积存在有限制时，即便函数在一点的值无穷，但面积可求。

例如的几何意义是：位于曲线
之下，X轴之上，直线x=0和x=a之间的图形面积，而x=a点的值虽
使无穷，但面积可求。

类型：
1.无穷区间反常积分
每个被积函数只能有一个无穷限，若上下限均为无穷限，则分区间积分。

2.无界函数反常积分
即瑕积分，每个被积函数只能有一个瑕点，多个瑕点则分区间积分。

3.混合反常积分
对于上下限均为无穷，或被积分函数存在多个瑕点，或上述两类的混合，称为混合反常积分。

对混合型反常积分，必须拆分多个积分区间，使原积分为无穷区间和无界函数两类单独的反常积分之和。

敛散性判断：
反常积分的敛散判断本质上是极限的存在性与无穷小或无穷大的比阶问题。

首先要记住两类反常积分的收敛尺度：对第一类无穷限
而言，当x→+∞时，f(x)必为无穷小，并且无穷小的阶
次不能低于某一尺度，才能保证收敛；对第二类无界函数而言，当x→a+时，f(x)必为无穷大，且无穷大的阶次不能高于某一尺度，才能保证收敛；这个尺度值一般等于1，注意识别反常积分。

反常积分的理解
反常积分又叫广义积分，是对普通定积分的推广，指含有无穷上限/下限，或者被积函数含有瑕点的积分，前者称为无穷限广义积分，后者称为瑕积分（又称无界函数的反常积分）。

反常积分就是积分区间是无界的，也就是区间可以有无穷大，也可以是有限区间函数在某点处无界。

反常积分的出现，是因为在实际应用和理论研究中，还会遇到一些在无限区间上定义的函数或有限区间上的无界函数，对它们也需要考虑类似于定积分的问题。

反常积分和定积分的区别：
反常积分可能出现积分区间无界的情况，而定积分只能在有限的区间上积分。

反常积分的被积函数可能存在瑕点（即无界点），而定积分的被积函数都是有界的。

反常积分可能出现积分后结果为无穷大的情况，而定积分的积分结果总是有限的。

反常积分和定积分的联系：
反常积分和定积分都是用来计算面积的。

反常积分的结果可能是一个数，也可能是一个无穷大，而定积分的结果是一个数。

反常积分和定积分的计算方法有很多相似之处，如换元法、分部积分法等。

反常积分的应用：
在物理学中，反常积分被广泛应用于处理具有无限大能量或质量的系统的问题。

在经济学中，反常积分可以用来计算具有无限时间跨度的投资或消费的累积效应。

在工程学中，反常积分可以用来分析具有无限大尺寸或无界范围的系统的性质。

反常积分的主值
反常积分是对定积分的概念进行推广后得到的，它异于通常的定积分，故称之为广义积分，也称之为反常积分。

对于在上的反常积分，有一类更特殊的积分定义为柯西主值积分，其中P.V.意为主值（Principal Value）。

上述积分的结果亦称为该积分的主值。

此外，在数学中，如果同时考虑积分区间的两端极限（无穷或函数无界点），即$lim(X →+\infty)\int(-X,X) f(x)dx$或$lim(η→0+) \int(a+η,b-η) f(x)dx$，其中$f(x)$在$a$的右领域和$b$的左领域内无界，或$lim(η→0+)(\int(a,b-η) f(x)dx+\int(b+η,c) f(x)dx)$，其中$f(x)$在$b$的领域内无界，如果收敛，则称相应的反常积分在主值意义下存在。

反常积分的主值是一个重要的概念，在数学、物理学等领域都有广泛的应用。