三年级不规则图形求面积

北师大版小学三年级数学下册教案第四单元：面积课题什么是面积数学第六册教学目标 1、结合具体实例和画图活动，认识图形面积的含义。

2、经历比较两个图形面积大小的过程，体验比较策略的多样性。

3、引导学生通过观察、比较、猜测、动手操作，培养学生自主学习和探究问题的习惯。

教学重点理解面积的含义。

教学难点体验比较策略的多样性学前分析学生已经学过了长度单位：毫米、厘米、分米、米、千米，并且学生了计算长方形和正方形的周长，而对于面积而言，学生是第一次碰到，对面积的概念也比较模糊。

教学过程Ò»¡¢ 游戏引入。

1、师：我们先来做一个涂色游戏。

男生派一个代表，女生也派一个代表，分别拿一张大纸给男生，拿一张小纸给女生，要求在白纸上用水彩笔涂上颜色，谁涂完谁就是冠军。

2、肯定会出现以下的情况：女生：肯定很高兴男生：肯定不愿意……要求公平3、师：为什么男生不愿意？而女生却很乐意？二、实践活动，感受面积概念。

1、认识物体表面。

（1）让学生拿出语文书和数学书，摸一摸封面，并说说有什么感受？学生可能有的答案：A、很光滑……B、平平的……C、数学书的封面要大……（2）再让学生摸一摸铅笔盒的面和桌子的面，谈谈感受。

（3）再摸摸自己的脸和手面……（4）师：教师指出这些面都是物体的表面，并板书：物体的表面。

2、认识平面图形。

（1）师：在黑板上画几个不同大小的平面图形。

（2）让学生观察，引导学生说说哪个图形大、哪个图形小？3、概括面积概念。

通过刚才的比较，我们知道物体的表面和图形是有大小的，怎么样区分它们的大小呢？我们用面积来表示。

板书：物体表面或图形的大小叫做它们的面积。

三、图形大小的比较策略。

1、比较一个长方形和一个正方形的面积大小。

课前让学生把书后附页中的图剪下来，并在课堂上准备好剪刀、尺、小方块、方格纸。

2、师：谁能告诉我们哪个图形面积较大？学生发表自己的意见。

3、组织学生动手操作、讨论交流自己的想法。

【例1】一根铁丝正好能围成一个边长为4分米的正方形，如果用这根铁丝围成一个长为5分米的长方形，这个长方形的面积是多少平方分米？周长相等，求出正方形周长就是长方形周长。

关键是求出长方形的宽。

周长：4×4=16（分米）长＋宽：16÷2=8（分米）宽：8－5=3（分米）面积：5×3=15（平方分米）答：这个长方形的面积是15平方分米。

【练习】1、一个长方形和正方形周长相等。

长方形的长是33厘米，宽是17厘米。

正方形的面积是多少平方厘米？原来长方形周长和现在长方形周长相等。

长方形周长：（33＋17)×2=10（厘米）正方形边长：100÷4=25（厘米）正方形面积25×25=625（平方厘米）答；正方形面积625平方厘米2、一个由铁丝围成的长方形，面积是56平方厘米，长是8厘米，现把这根铁丝重新围成宽是4厘米的长方形，这个新围成的长方形面积是多少平方厘米？宽：56÷8=7（厘米）长方形周长（8＋7)×2=30（厘米）现在长方形的长30÷2－4=11（厘米）现在面积：4×11=44（平方厘米）答：新长方形的面积是44平方厘米。

【例2】把一张长18厘米、宽6厘米的长方形纸，剪成边长为3厘米的小正方形纸，能剪成多少个这样的小正方形纸？长边：18÷3=6（个）宽边：6÷3=2（个）总个数：6×2=12（个）答：能剪成12个这样的小正方形纸。

长方形被分成若干个小正方形题型：1.求长有几个正方形边长，2.求宽有几个正方形边长。

3.长有几个，宽有几个的乘积就是小正方形的数量。

【练习】1、把一个长20厘米、宽16厘米的长方形分割成边长为4厘米的小正方形，最多能分割成多少个这样的小正方形？长边：20÷4=5（厘米）宽边：16÷4=4（个）一共：4×5=20（个）答：最多可以分割20个这样的小正方形。

三年级下认识面积小朋友们，在我们三年级的数学学习中，有一个非常有趣也很重要的概念，那就是面积。

今天，就让我们一起来好好认识一下它吧！什么是面积呢？想象一下，我们有一块大大的黑板，还有一张小小的课桌。

黑板表面的大小，和课桌表面的大小是不一样的。

这个“表面的大小”就是面积啦。

简单来说，面积就是物体表面的大小。

那我们怎么去衡量面积的大小呢？这就需要用到一些标准的单位。

就好像我们量身高用厘米、米，量体重用千克一样，量面积也有专门的单位哦。

在日常生活中，我们常用的面积单位有平方厘米、平方分米和平方米。

先来说说平方厘米吧。

小朋友们可以拿出尺子，画一个边长为 1 厘米的正方形。

这个正方形的面积就是 1 平方厘米。

1 平方厘米有多大呢？差不多就是我们大拇指指甲盖的大小。

那如果要测量像橡皮这样比较小的物体的面积，就可以用平方厘米作单位。

再来说说平方分米。

同样的方法，画一个边长为 1 分米的正方形，它的面积就是 1 平方分米。

1 平方分米比 1 平方厘米大多啦，大概是我们手掌那么大。

像我们的课本封面，就可以用平方分米来测量它的面积。

最大的单位要数平方米啦。

画一个边长为 1 米的正方形，它的面积就是 1 平方米。

1 平方米可就更大了，差不多是我们家里放一张小桌子的地方那么大。

教室的地面面积、房间的面积，就可以用平方米来测量。

知道了面积单位，那我们怎么去测量一个物体的面积呢？如果是一个规则的长方形或者正方形，我们可以用公式来计算。

对于长方形来说，面积等于长乘以宽。

比如说，有一个长方形的黑板，长是 4 米，宽是 2 米，那么它的面积就是 4×2 ＝ 8（平方米）。

正方形的面积就更简单啦，因为正方形的四条边都相等，所以面积等于边长乘以边长。

假如有一个正方形的手帕，边长是 3 分米，那它的面积就是 3×3 ＝ 9（平方分米）。

但是，如果是一个不规则的图形，那该怎么办呢？这时候，我们可以用数格子的方法。

把这个不规则的图形放在一个方格纸上，然后数有多少个完整的格子，再加上不完整的格子进行估算。

1.在小学数学中，图形的面积是如何编排的？分析在面积公式的推导中所蕴含的数学思想和方法。

2. 方格纸和坐标的关系是怎样的？你认为在小学阶段是如何体现的？在小学数学中，图形的面积编排如下：三年级（下册）：面积与面积单位，长方形和正方形的面积。

1、结合实例认识面积的含义，能用自选的单位估计和测量图形的面积，体会并认识面积单位（平方厘米、平方米、平方千米、公顷），会进行简单的单位换算。

2、探索并掌握长方形、正方形的面积公式，能估算出给定的长方形、正方形面积。

五年级（上册）：多边形面积的计算1、利用方格纸或割补等方法，探索并掌握平行四边形、三角形和梯形的面积公式2、会计算由上述图形构成的组合图形的面积。

3.、能用方格纸估计不规则图形的面积。

六年级（上册）：圆结合具体情景，探索并掌握圆的面积公式，会计算简单组合图形的面积在面积公式的推导中蕴含了以下几个方面的数学思想和方法：六年级下册：圆柱的侧面积和表面积结合具体情景，探索并掌握圆柱的表面积公式。

在面积公式的推导中所蕴含的数学思想有：猜想、实验、转化、归纳等重要的数学思想方法，还渗透了极限思想、函数思想、等积变形思想等。

例如：从三年级开始学习长方形的面积计算，教材中不仅安排了文字公式，还介绍字母公式S=a×b;再如，圆面积公式S=πR²,S是R的函数，这些公式中既有一次函数也有二次函数。

如编排长方形和正方形的面积计算时，渗透了操作、归纳的思想，编排多边形的面积计算时，渗透了转化、归纳思想，平面图形面积公式的推导中，从平行四边形、三角形、到梯形的面积公式的推导都是以转化、归纳的思想方法为核心。

研究三角形、平行四边形的面积公式时，都转化成我们学过的平面图形。

在转化的过程中面积保持不变，把不会求面积的图形转化成会求面积的平面图形。

如：把平行四边形运用割补的方法把它变成长方形，求出长方形的面积，也就求出了平行四边形的面积。

找出平行四边形与长方形之间的关系，得出平行四边形的面积=底×高。

三年级秋季班第14讲-⾯积计算-教师版⾯积计算【教学⽬标】1、在教师指导下，通过探索（在这⾥是先观察，再动⼿⽐较）所给出的图形（在平⾯上，由线段围成的封闭图形）的⼤⼩，初步体会到这种图形的⼤⼩就是它们的⾯积。

2、学会⽤⽅格的多少来表⽰⾯积。

3、认识⾯积单位，平⽅⽶（2m ）；会⽤平⽅⽶来表⽰较⼤图形的⾯积。

4、探索与掌握长⽅形与正⽅形的⾯积计算公式；会⽤厘⽶⽅格来表⽰图形的⾯积。

5、认识⾯积单位平⽅厘⽶（2cm ）。

初步建⽴1平⽅厘⽶的⾯积概念.【教学重点】1、⽤⽅格的多少表⽰⾯积。

2、认识⾯积的单位：平⽅⽶，初步建⽴1平⽅⽶的量感。

3、长⽅形、正⽅形的⾯积计算公式。

4、长⽅形、正⽅形的⾯积计算公式的含义。

【教学难点】1、通过数⽅格，得出不规则图形的⾯积。

2、长⽅形、正⽅形⾯积公式的应⽤。

3、长⽅形、正⽅形的⾯积计算公式的含义。

【复习巩固】1、⼝算：（1）760?=42 （2）5409÷=60 （3）8005?=4000 （4）40050÷=8（5）100080-=920 （6）1258?=1000 （7）1437373-+=143（8）83790??=0 （9）13443?-?=40 （10）1375446-+=1292、分拆计算：（1）5285?=2640 （2）4687÷=666鬃鬃鬃50052500205100854052852640?=?=?=?= 420760487664687666÷=÷=÷=3、竖式计算（打※的要验算）：（1）60256?=36150 （2）30455÷=609 （3）62143÷=※2071160256 361506095304530 45 45 0621 21 4 3 1207136213621316214?=+=验算：4、递等式计算，能简便计算的要简便计算：（1）182569318++（2）4564443+÷解：()182318569=++ 解：()4563331113=++÷5005691069=+=456333311134561113756737604=+÷+÷=++=+=【教学过程】⼀、填空题：1、⾯积为1平⽅厘⽶的正⽅形，它的边长是（ 1厘⽶）。

几何图形解题方法在实际生产和生活中，几何形体往往不是以标准的形状出现,而是以比较复杂的组合图形出现，很难直接利用公式计算其面积或体积.如果在保持图形的面积或体积不变的前提下，对图形进行适当的变换，就容易找出计算其面积或体积的方法。

（一）添辅助线法有些组合图形按一般的思考方法好像已知条件不足,很难解答。

如果在图形中添加适当的辅助线,就可能找到解题的途径。

辅助线一般用虚线表示。

＊例1 求图40-1阴影部分的面积。

（单位：平方米）(适于三年级程度）解：图40-1中,右边两个部分的面积分别是20平方米和30平方米，所以可如图40—2那样添上三条辅助线，把整个长方形分成5等份。

这样图中右边的五个小长方形的面积相等。

同时，左边五个小长方形的面积也相等.左边每个小长方形的面积是：25÷2=12。

5（平方米）所以，阴影部分的面积是:12。

5×3=37.5（平方米）答略。

*例2 如图40—3,一个平行四边形被分成两个部分,它们的面积差是10平方厘米，高是5厘米.求EC的长.（单位：厘米)（适于五年级程度)解：如图40—4，过E点作AB的平行线EF，则△AEF与△ABE是等底等高的三角形。

所以，△AEF的面积与△ABE的面积相等.小平行四边形EFDC的面积就是10平方厘米。

因为它的高是5厘米,所以，EC=10÷5=2（厘米)答：EC长2厘米。

＊例3 如图40-5，已知图中四边形两条边的长度和三个角的度数,求这个四边形的面积.(单位：厘米)(适于五年级程度）解：这是一个不规则的四边形，无法直接计算它的面积。

如图40—6,把AD和BC两条线段分别延长,使它们相交于E点.这样，四边形ABCD的面积就可以转化为△ABE的面积与△DCE的面积之差。

在△ABE中，∠A是直角，∠B=45°，所以∠E=45°，即△ABE是等腰直角三角形。

所以AB=AE=7（厘米),则△ABE的面积是：7×7÷2=24。

第十讲：面积的实际应用知识梳理【知识要点】1、周长:封闭图形一周的长度，是它的周长。

长方形的周长 =（长+宽）×2正方形的周长 = 边长×42、面积：物体的表面或封闭图形的大小就是它们的面积。

边长是1厘米的正方形的面积是1平方厘米。

边长是1分米的正方形的面积是1平方分米边长是1米的正方形的面积是1平方米长方形的面积 = 长×宽正方形的面积 = 边长×边长3、一个图形剪掉一部分，面积一定会减少，但周长不一定会减少。

4、掌握换算的方法（1）高级单位化成低级单位：高级单位的数×进率大单位化小单位添0，如2平方米=（200）平方分米（想：平方米大，所以是大化小添0，因为1平方米=100平方分米，应该在2后面添两个0.）(2)低级单位聚成高级单位：低级单位的数÷进率小单位化大单位去0，如20000平方米=（2）公顷，（想：平方米小，所以是小化大去0，因为1公顷=10000平方米，应该去掉2后面的四个0.）5、周长相等的两个长方形，面积不一定相等。

面积相等的两个长方形，周长也不一定相等。

6、长方形和正方形的面积相等时，正方形的周长小。

7、长方形和正方形的周长相等时，正方形的面积大。

（如用同样长的绳子围成的正方形面积比长方形的面积大）面积单位换算1平方千米 = 100公顷 1公顷=10000 平方米 1平方米=100 平方分米 1平方分米=100平方厘米【例题一】小林要从左边的纸上剪下一个最大的正方形。

剩下部分是什么图形？它的面积是多少平方厘米？【拓展训练】一个长方形，长16分米，宽12分米，在这个长方形上尽可能剪下一个正方形，正方形的面积是多少？剩下图形的面积是多少？【例题二】求下列图形的周长。

12厘米 15厘米 15厘米12厘米 12厘米 9米10米 3米4米【拓展训练】（单位：cm ）【例题三】李奶奶家房子东面有一块长方形菜地，菜地一边紧挨着墙壁（如右图），少先队员们要给李奶奶的菜地围上篱笆，需要准备多长的篱笆？这块菜地的面积是多少平方米？【拓展训练】李大爷靠东墙围了一个羊圈，算出这个羊圈的占地面积？如果要砌上围墙，围墙的长度应该是多少米？【例题四】一块面积有72平方分米的长方形台布，长9分米，它的宽是多少？57 522 18米 3米 墙18 25米东墙【拓展训练】一块正方形的喷水池的周长是20米，它的边长是多少米？面积是多少平方米？【例题五】3平方米=（）平方分米 5平方分米=（）平方厘米700平方厘米=（）平方分米600平方分米=（）平方厘米30平方分米=（）平方厘米 8000平方分米=（）平方米【拓展训练】1、教室地面的面积大约是60（），也就是6000（）。

面积的估测（1）教学内容：九年义务教育课本三年级数学第二学期第4页面积的估测（1）教学目标：1、能用数方格的方法估测出不规则平面图形的面积。

2、初步体会“四舍五入”的思想方法。

重点、难点：会用“四舍五入”的思想方法来估测出不规则平面图形的面积。

教学准备：树叶实物、透明方格纸等。

教学过程：一、导入新知（出示小胖、小巧在公园里捡树叶图）1、说说图上的小朋友在干什么？2、师：（出示树叶实物）老师这里也有一片树叶，这片树叶的面积有多大呢？这就是我们今天这节课要探究的新本领。

（出示课题：树叶的面积）二、探究新知1、师：想一想，怎样来计算树叶的面积？生小组讨论，交流。

2、师：小朋友真聪明，想到了好多的方法。

但在用这些方法计算树叶的面积时，肯定会出现好多不同的结果，所以，我们的好朋友小丁丁想出了一个好办法，将树叶放在透明方格纸下进行测量，这样测量的结果就会很接近，比较科学。

（出示投影）3、指导学生像小丁丁那样把树叶放在透明方格纸下进行测量。

4、讨论交流：不满一格的怎么办？5、师统一测量方法：大于等于半格的算一格，小于半格的舍去。

归纳，完成填空：整格 31格大于等于半格 17格树叶的面积大约为 48个格树叶的面积大约为 48平方厘米三、巩固练习1、计算“脚印”的面积。

2、生完成练习册第2页，后交流。

四、课堂总结今天我们学习了什么新本领？你有什么收获？平方分米教学内容：P5平方分米教学目标：1．认识面积单位dm2,建立1dm2的直观表象，知道它的写法。

2．知道dm2与它相邻的两个面积单位之间的进率，并会进行简单的单位换算。

教学重点和难点：重点：认识面积单位dm2,知道dm2与它相邻的两个面积单位之间的进率难点：会进行dm2与它相邻的两个面积单位之间的单位换算。

教学过程：一、旧知引新知1．回顾：上学期我们学习了有关“面积”的知识，什么是面积？已经学过的面积单位有哪些？它们之间的进率是多少？（生口答，师板书）：2． 师：今天我们继续来学习有关“面积”的知识。

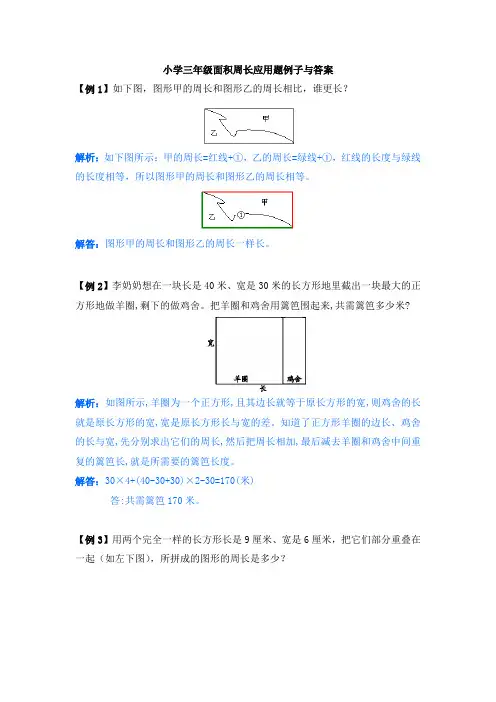
小学三年级面积周长应用题例子与答案【例1】如下图，图形甲的周长和图形乙的周长相比，谁更长？解析：如下图所示：甲的周长=红线+①，乙的周长=绿线+①，红线的长度与绿线的长度相等，所以图形甲的周长和图形乙的周长相等。

解答：图形甲的周长和图形乙的周长一样长。

【例2】李奶奶想在一块长是40米、宽是30米的长方形地里截出一块最大的正方形地做羊圈,剩下的做鸡舍。

把羊圈和鸡舍用篱笆围起来,共需篱笆多少米?解析：如图所示,羊圈为一个正方形,且其边长就等于原长方形的宽,则鸡舍的长就是原长方形的宽,宽是原长方形长与宽的差。

知道了正方形羊圈的边长、鸡舍的长与宽,先分别求出它们的周长,然后把周长相加,最后减去羊圈和鸡舍中间重复的篱笆长,就是所需要的篱笆长度。

解答：30×4+(40-30+30)×2-30=170(米)答:共需篱笆170米。

【例3】用两个完全一样的长方形长是9厘米、宽是6厘米，把它们部分重叠在一起（如左下图），所拼成的图形的周长是多少？解析：此题主要考察学生通过解决问题，培养学生灵活应用所学知识解决问题的能力。

如右上图所示：①平移后是③，②平移后是④，平移后正好是边长9厘米的正方形，所以拼成的图形的周长是一个边长为9厘米的正方形，正方形的周长=边长×4，列式为4×9。

解答：4×9=36（厘米）答：所拼成的图形的周长是36厘米。

【例4】如图所示，这个图形的周长是多少米？解析：如果按箭头所指的方向将EF边向上移，将DF边向右移，就能形成一个长是8米、宽是5米的长方形，这个长方形的周长是8+5=13（米），13×2=26（米），所以该图形的周长就是26米。

解答：8+5=13（米） 13×2=26（米）答：篱笆的总长度是26米。

【例5】李叔叔新建了四个养殖厂，他想给饲养区都围上木栅栏（水塘周围不围），你能帮他算一算一共需要多长的木栅栏吗？解析：水塘的周围是4个长方形，而水塘是个正方形，由这5个图形组成了一个大正方形，如果把长方形和正方形的周长都算出来，再减，会比较麻烦，因为有重复的边。

学而思三年级奥数第九讲长方形与正方形知识点：长方形的面积=长×宽正方形的面积=边长×边长不规则图形面积的计算方法与技巧合理平移、分析、转化等，即转化为标准的图形来进行面积计算。

例1 有一长方形草坪，长31米，宽26米，草坪中间留了1米的路，路把草坪分成4块（如图），求草坪的实有面积是多少？例2如下图，求出阴影部分的面积。

（四角是边长为10厘米的正方形）例3 如图，在一个正方形的水池周围，围绕着宽5米的小花园，小花园的面积为300平方米，水池的面积是多少平方米？例4 如图，求出阴影部分的面积。

（单位：厘米）例5 如图，图中大正方形比小正方形的边长多4厘米，大正方形的面积比小正方形的面积多96平方厘米，大正方形和小正方形的面积各是多少？例6如图，大正方形的面积比小正方形的面积大32平方厘米，求这两个正方形的面积。

（单位：厘米）例7 如图，正方形中套着一个长方形，正方形的边长是12分米，长方形的四个角的顶点恰好把正方形的四条边都分成两段，其中长的一段是短的一段的3倍，这个长方形的面积是多少？例8 用同样大小的长方形小纸片，摆成了如下图的形状，已知小纸片的宽度是12厘米，求阴影部分面积的和。

同步练习1、用长36厘米的一根铁丝围成一个正方形，它的面积是多少？用这根铁丝围成一个长12厘米的长方形，它的面积是多少？2、如图，有一块长方形土地，长是宽的2倍，中间有一座雕塑，雕塑的底面是一个正方形，周围是花圃，花圃的面积是多少平方米？（单位：米）3、下图是由6个相等的三角形拼成的图形，求这个图形的面积？4、有两个相同的长方形，长13厘米，宽5厘米，如果把它们按如下图叠放在一起，这个图形的面积是多少？5、有一块菜地长16米，宽8米，如下图菜地中间留了2条宽2米的路，把菜地平均分成四块，每一块地的面积是多少？6、一个正方形，如果边长增加2厘米，它的面积增加16平方厘米，求原正方形面积？7、个周长为60分米的长方形，把它的长缩短6分米后，再把它的宽增加6分米，得到的新长方形面积比原来多24平方分米。

不规则几何图形面积计算方法有一次坐车，曾与一位大学一年级的学生坐邻座。

问她现在还学不学数学，她说正学呢，学微积分。

问微积分有什么用，她想了想，说：“可以求不规则图形的面积”。

我将手拍在我们前面座椅的靠背上，问：“用你高中以前的知识，你怎么求我的手掌印的面积？”她马上说：“这没有办法求。

我们求面积都是求的规则图形的面积。

这个没有办法求。

”她没有用过新课程下的数学教材。

对于用过新课程下的数学教材的学生来说，这样的问题，小学生应当能够解决了。

新世纪小学数学教材安排了探索不规则图形及物体的测量方法，如，“估计自己脚印的面积”的活动，“学生可以在脚印上画出透明的正方形格子，由此进行估计。

对于感兴趣的学生，教师还可以引导他们计算出鞋印覆盖住的整方格数，得到鞋印面积的不足近似值；再计算出被鞋印接触过的所有方格数，得到鞋印面积的过剩近似值，鞋印的实际面积介于二者之间。

根据经验，学生还可能认识到方格分得越细，不足近似值和过剩近似值越接近，这种认识实际上蕴涵了微积分的基本思想。

[1]”大方格不能上文说“根据经验，学生还可能认识到……”，似乎是编写者“一厢情愿”的猜度。

我们看到下面的材料，想来你会体会到编写者这样设计的意义和价值。

这是一位教师在上课中的实录节选。

例2[2] 求一块不规则图形的面积．这与数学中的常规问题是不同的，我们在数学中面对的一般都是规则图形，可以直接用公式计算，或者通过适当割补后再用公式计算．如何解决这一问题呢?我们把它交给学生，竟然得到了如下一些成果：方法1 将图形放在坐标纸上，也即将图形分割，看它有多少个“单位面积”．[1]义务教育课程标准实验教科书·数学教师教学用书(四年级上册)·致教师（一），北京师范在学出版社，[2]试谈以人为本的三维课堂教学，/jy zx/Print.asp方法2 将图形从内外两个方面用规则图形(或规则图形的组合)逼近．方法3 将这块图形用一个正方形围住，然后随机地向正方形内扔“点”(如小石子等小颗粒)，当点数P足够大时，统计落入不规则图形中的点数A，则图形的面积与正方形面积的比约为．方法4“称量”面积：在正方形区域内均匀铺满一层细沙，分别称得重量是P(正方形区域内细沙重)、A(所求图形内细沙重)，则所求图形的面积与正方形面积的比是．我们欣赏一下学生的思路，你会发现，这里的每一种方法都有极其深刻的背景。

估测不规则图形的面积教学内容：青岛版小学数学三年级下册第54页 6。

7.8题.教学目标1。

进一步感知面积单位平方厘米、平方分米、平方米的大小，能自选单位正确估计不规则的2.经历观察、估计、测量图形的面积的过程，进一步发展学生的空间观念。

3.能借助方格图估算不规则图形的面积，在估算面积的过程中，体验解决问题策略的多样性，培养图形面积的大小，能用数方格的方法计算一些不规则图形的面积。

初步的估算意识和估算习惯,体验估算的必要性和重要作用.4。

在估测图形的面积的过程中，体会数学与现实生活的密切联系，感受数学的应用价值。

教学重难点过程中，体会数学与现实生活的密切联系，感受数学的应用价值。

教学重点：自选位估测图形的面积.教学难点：估测图形面积的方法.教具、学具多媒体课件、方格纸、1平方厘米和1平方分米纸片。

教学过程一、创设情境，提出问题1。

复习铺垫：同学们，上节课我们学习了面积和面积单位，谁来说一说常用的面积单位有哪些?（平方米、平方分米、平方厘米）谁举例说明1平方米、1平方分米、1平方厘米有多大？学生举例（通过举例，学生会进一步加深对面积单位平方厘米、平方分米、平方米的大小的感知，为估测图形的面积做好了准备）2.根据对1平方厘米,1平方分米,1平方米的感知，你能估计出黑板的面积吗? 用哪个单位估计比较合适？学生感知到用1平方米来估计，黑板有四块，一块是1平方米,一共是4平方米.提问：估计黑板的面积就是估计什么形的面积？（长方形）3.创设情境:星期天，老师去爬山的时候，看到地上有一片树叶非常漂亮，就带了回来。

出示树叶图片。

看到这片树叶，你们想知道什么？预设：学生可能会说：这是什么树的树叶？它有多大？它的面积大约是多少？……3。

导入新课:这片树叶的面积大约是多少呢？先让学生指一指树叶的面积是哪一部分？指名几名学生上台指一指。

树叶的形状是我们学过的长方形或其它图形吗?(不是）像这种图形叫不规则图形,今天我们就来学习怎样估测不规则图形的面积。

4分米图34名师导航学校三年级奥数辅导讲义长方形、正方形面积思路点拨：1、对于不规则图形的面积，或所求图形面积的必要条件不充分一般采取 大面积 - 小面积2、对于求几个图形的面积和，可以切割，拼接。

例1、一块长方形土地，长是宽的2倍，中间有一座雕塑，雕塑的底面是一个正方形，周围是草坪，草坪的面积是多项式少平方米？例2、右图是由6个相等的三角形拼成的图形，求这个图形的面积。

例3、已知图3中大正方形比小正方形的边长多4厘米，大正方形面积比 小正方形多96平方厘米。

大正方形和小正方形的面积各是多少？例4、正方形中套着一个长方形，正方形的边长是15厘米，长方形的四个角的顶点， 恰好分别把正方形四条边都公成两段，其中长的一段是短的2倍。

这个长方形的面积是多少平方米？例4、已知正方形ABCD的边长为6分米，长方形BCEF和长方形AGHD的面积分别为24平方分米和20平方分米，求阴影部分和面积。

例5、一个边长是7厘米的正方形纸片，最多能裁出多少个长是4厘米，宽是1厘米的纸条，请画图说明。

练习与思考1.用长36厘米长的一根铁丝围成一个正方形，它的面积是多少？用这根铁丝围成一个长12厘米的长方形，它的面积是多少？2.有一个长方形的市民广场，长100米，宽80米。

广场中间留了宽4米的人行道，把广场平均分成四块（如图6），每一块的面积是多少？3.下图是由12个相等的三角形拼成的，这个图形的面积是多少？4.已知大正方形的面积比小正方形多52平方分米，大正方形比小正方形的边长多2分米。

小正方形的面积是多少？大正方形的面积是多少？5.是由9个小长方形组成的，面积分别是1平方米，2平方米，3平方米，4平方米，5平方米，那么，A 号长方形和面积是多少呢？6.一个正方形中套着一个长方形，已知正方形的边长 是16分米，长方形的四个角的顶点恰好把正方形四条边 都分成两段，其中长的一段是短的3倍。

阴影部分的面积 是多少？7.图中阴影部分的面积是多少？8.把一块长6分米，宽5分米的长方形钢板，截成长3分米，宽2分米的小长方形钢板，最多能截几块？请画图说明。

第10讲图形问题抢答赛——长方形和正方形的面积[教学内容]《数学》春季全国版，3年级第10讲“图形问题抢答赛——长方形和正方形的面积”。

[教学目标]知识技能1．使学生在观察、操作等活动中理解面积的含义。

2．使学生经历比较图形面积大小的过程，体验多种计算策略。

数学思考：通过直观观察、动手操作活动理解面积的意义。

问题解决能在日常生活中发现与长方形与正方形面积有关的数学问题，并学会解决与面积有关的数学问题。

体验与他人合作交流解决问题的过程。

情感态度在学习的活动中，体会数学与生活的联系，锻炼数学思考能力，发展空间观念，激发进一步学习和探索的兴趣。

[教学重难点]教学重点学会求不规则图形面积的方法。

教学难点规则图形面积的求法。

[教学准备]动画多媒体语言课件。

第一课时教学过程：（一）教学例1例1：下面图形中的每一个小方格都表示1平方厘米，这个图形的面积是多少平方厘米？（1）学生观察题目以及图示，找出计算方法。

（2）学生之间讨论。

（3）教师分析师：我们看到的这个图形是不是我们常见的长方形和正方形呀？生：不是的。

师：哦，那么我们怎么样计算它的面积呢？生：我们可以利用数格子方法，告诉我们一个格子的面积是1平方厘米，那么我们数一数就可以了。

师：对。

说的很好。

不过图中有的格子是半个格，怎么数呢？学生交流：割补法。

（4）学生互相说说面积是多少。

提示：出示辅助线下一步：动画展示，右边的三角形移到左边，与左边的三角形拼成正方形。

答案：2×4=8（平方厘米）答：这个图形的面积是8平方厘米。

师：看来我们对于不规则的图形还可以利用数或者割补的方法计算面积，现在老师可要考考你们了哦。

课件出示：变式练习下面两个图形的面积各是多少平方厘米？（每小格表示1平学生比较方法的简便性。

学生独立完成便式练习。

示，帮助分析。

学生理解平移的作用。

方厘米）（1）学生独立完成，找出求面积的方法，并说明理由。

（2）同桌说一说面积是多少。

（3）教师核对答案。

三年级不规则图形周长怎么计算
三年级不规则图形周长的求法有：
1、将图形分为几个规则图形。

2、分别求出各个规则图形周长。

3、将各个周长加起来，结果就是不规则图形周长。

不规则图形不是以基本图形的形状出现，而是由一些基本图形组合、拼凑成的，它们的面积及周长无法应用公式直接计算。

环绕有限面积的区域边缘的长度积分，叫做周长，也就是图形一周的长度。

不规则的图形计算面积
1、分图法：用分割法或添补法，把不规则图形分成会计算的简单图形。

2、填补法：把不规则图形补成一个规则的图形，再以总面积减去填补上去的图形的面积。

3、找条件：分别计算简单图形的面积。

4、算面积：最后求和或差。

三年级下册数学期末复习专题讲义-5.面积【知识点归纳】1.面积的意义：物体的表面或封闭图形的大小，就是他们的面积。

2.长度单位与面积单位的区别：用长度单位表示物体的长短或封闭图形一周的长度，用面积单位表示物体表面或封闭图形的大小。

注：面积和周长是不能相比较的；分清楚什么时候填长度单位，什么时候填面积单位。

3.比较两个图形面积的大小，要用统一的面积单位来测量和比较。

4.常用的面积单位有：平方厘米（cm2）；平方分米（dm2）；平方米（m2）。

边长1厘米的正方形面积是1平方厘米。

□ 1平方厘米=100平方毫米边长1分米的正方形面积是1平方分米。

□ 1平方分米=100平方厘米边长1米的正方形面积是1平方米。

□ 1平方米 = 100平方分米边长100米的正方形面积是1公顷□ 1公顷 = 10000平方米边长1千米的正方形面积是1平方千米。

□ 1平方千米=100公顷5.测量土地的面积时常常要用到更大的面积单位：公顷、平方千米。

6.面积单位间的换算关系：大单位化成小单位，用大单位前面的数乘进率；小单位化成大单位，用小单位前面的数除以进率。

1平方千米= 100公顷；1公顷=10000平方米；1平方米=100平方分米；1平方分米=100平方厘米；1平方厘米=100平方毫米.7.使用面积单位时.：①比较小的土地面积，如：公园、体育场馆、超市、果园、广场等一般情况下填“公顷”；②比较大的土地面积，如：某城市的占地面积、国家的面积、江河湖海的面积等一般情况下填“平方千米”。

8.长方形的面积=长×宽；长 = 面积÷宽；宽 = 面积÷长9.正方形的面积=边长×边长10.长方形的周长=(长+宽)×2 ；宽 = 周长÷2—长；长 = 周长÷2—宽11.正方形的周长=边长×4 ；正方形的边长=周长÷412.铺地砖问题：①先算出所铺地面的总面积；②计算出每块地砖的面积；③将这两个面积统一成相同的面积单位；④地砖的总块数=所铺地面的总面积÷每块地砖的面积.13.计算格点图形不规则图形的面积时，将不够一个单位的面积拼凑成几个单位的面积；再加上所有整个单位面积就是整个图形的面积.注意：面积相等的两个图形，它们周长不一定相等。

1、你有什么好的方法计算所给图形的面积呢？(单位：厘米)
方法一：采用分割法，可给原图分成两个长方形(图1或图2)，两个长方形的总面积就是所求的面积．
图1面积是：4×（9+3）+9×3=75(平方厘米)
图2面积是：（9+4）×3+9×4=75(平方厘米)
方法二：采用补图法，如果补上一个边长是9厘米的正方形(图3)，就成了一个大长方形．因此用这个长方形的面积减去所补正方
形的面积，就是要求的图形面积
图3面积是：
（4+9）×（9+3）-9×9=75(平方厘米)
2、如图是学校操场一角，请计算它的面积(单位：米)
【解析】可以在图中添上一条辅助线，把多边形切割成上下两个长方形或左右两个长方形；也可以把多边形补充完整，成为一个长方形；
方法一：
30×40+20×（30+40）=2600(平方米)
方法二：
20×30+40×（20+30）=2600(平方米)
方法三：
（40+30）×（20+30）-30×30=2600(平方米)。

什么是面积
轻松准备
面积就是物体的表面或封闭图形的大小。

比较两个图形面积的大小时，可以把两个图形叠放在一起，通过剪一剪、拼一拼，看哪个图形的表面大，哪个图形的面积就大。

比较不规则图形的面积大小时，可以用数小方格、数小三角形的办法来解决。

快乐学习
1．摸一摸身边数学书的封面、铅笔盒盖的面、橡皮的正面，比一比哪一个面的面积最大，哪一个面的面积最小？
2.数下面三个图形中的小方格，说出哪个面积最大？哪个面积最小？
3.下面方格中各个图形的面积大小一样吗？
4．哪个图形的面积大，哪个图形的面积小？
5．仔细观察，哪个物体的表面大？
6．下面方格中的图形像什么？比较两个图形的面积大小。

7．下面图形的面积哪个大？
8．数一数每个图形的面积等于几个方格那么大。

9．在下面的方格里画一个正方形和一个三角形，使正方形面积正好是三角形面积的2倍。

10．填空。

图②的面积是图①面积的( )倍，图③的面积是图①面积的( )倍。

拓展提高
11.下面两个图形的面积哪个大？
12.设计几个你喜欢的图案，画在下面的方格里，要求它们的面积都要等于7个方格。

13.下面三个图形中，哪两个图形的面积相等？请把面积相等的两个图形涂上蓝色。

14.利用方格网数出下面图形的面积。

答案与点拨
3．一样
4．左边的大，右边的小。

5．左边物体表面大。

6．像桌子和椅子，两个图形的面积同样大。

7．右边图形面积大。

8．每个图形的面积都是8个方格。

10. 4 3
11．左边图形面积大。