《徐翠微计算方法引论》
- 格式:doc
- 大小:2.07 MB
- 文档页数:30


计算方法引论今天,计算方法正在深刻地影响着我们的生活,但是大多数人对这些方法一无所知。
本文旨在解释计算方法的内涵,介绍它如何在科学研究和工程设计中发挥作用,并就计算方法的发展前景及可能的改进提出建议。
计算方法的基本含义是使用计算机完成计算或信息处理任务,以达到实现特定功能的目的。
它是一种基于计算机科学的方法,可以将定义问题转换为可解决问题,从而提供我们有效的解决方案。
计算方法包括算法设计、编程语言、数学统计和信息论。
计算方法有助于解决复杂的现实问题,在工程设计、金融分析、社会科学研究、语音识别和机器人技术等领域均有广泛的应用,但它也可用于图像处理、语音处理、人工智能和虚拟现实。
计算方法的应用非常普遍,可以提高数据处理的效率,使系统中的任务变得更容易,最大限度地减轻人的劳动强度。
此外,计算方法也可以应用于科学研究。
例如,统计建模可以帮助我们理解和预测未来趋势,机器学习可以帮助我们建立更复杂的模型,以发掘隐藏的结构信息,从而发现未知的规律。
计算方法的运用有助于加快科学研究水平的提高,为研究者提供更多的参考资料,更好地了解特定领域的现象。
计算方法可以持续改进,以应对现代社会不断提出的新问题。
随着计算机科学和信息技术的发展,计算方法能够更好地应对复杂的现实问题,并覆盖更多的领域。
计算方法需要人类介入,并受人类知识、技能和思考动力的驱动,因此可以推动社会发展。
自现代信息技术的出现以来,如今人们正在构建更复杂的数学模型,以提高信息的获取效率,并以此为基础提出更高效的解决方案。
此外,计算方法也在持续改进以应对不断增加的信息量,使得可以从更大范围的数据中进行研究。
总之,计算方法是不可或缺的基础,在当今社会中发挥着重要作用。
除了有助于工程设计和科学研究外,它还可以改进我们的日常生活。
因此,计算方法也许是我们未来发展的重要力量,值得我们继续深入研究。
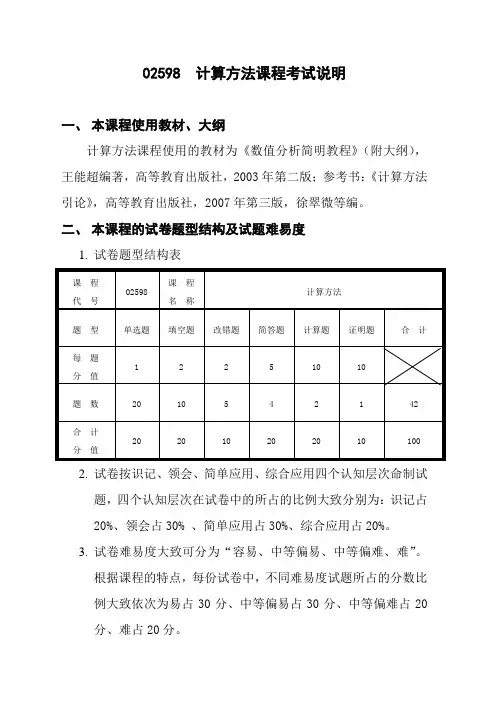
02598 计算方法课程考试说明一、本课程使用教材、大纲计算方法课程使用的教材为《数值分析简明教程》(附大纲),王能超编著,高等教育出版社,2003年第二版;参考书:《计算方法引论》,高等教育出版社,2007年第三版,徐翠微等编。
二、本课程的试卷题型结构及试题难易度1.试卷题型结构表2.试卷按识记、领会、简单应用、综合应用四个认知层次命制试题,四个认知层次在试卷中的所占的比例大致分别为:识记占20%、领会占30% 、简单应用占30%、综合应用占20%。
3.试卷难易度大致可分为“容易、中等偏易、中等偏难、难”。
根据课程的特点,每份试卷中,不同难易度试题所占的分数比例大致依次为易占30分、中等偏易占30分、中等偏难占20分、难占20分。
三、各章内容分数的大致分布四、各章内容的重、难点五、各题型试题范例及解题要求1.单项选择题(每小题1分,共20分)要求:在下列每小题的四个备选答案中选出一个正确的答案,并将其字母标号填入题干的括号内。
范例:解非线性方程0xf的牛顿切线法在单根*x附近的收(=)敛速度为()A.四阶B.二阶C.三阶D.一阶解答:( B )2.填空题 (每小题2分,共20分)要求:直接将答案填在横线上,不需要写出过程。
范例:向量范数满足的三个性质为非负性, ,三角不等式性。
解答:齐次性3.改错题(每小题2分,共10分)要求:把改正后的正确叙述写出来。
范例:3.141是 3.14159265...π=的四位有效数字。
解答:“四位”改为“三位”4.简答题(每小题5分,共20分)要求:简要答出要点。
范例:何谓龙贝格算法,其优点主要是什么?解答:将收敛相对缓慢的梯形序列T通过加工得到迅速收敛的n龙贝格序列即为龙贝格算法。
主要优点是精度高,算法简单,计算量小。
5. 计算题(每小题10分,共20分) 要求:写出主要过程 范例:已给数据表:(1)用复化梯形法计算积分的近似值。
(2)用辛甫生法计算积分的近似值。



计算方法引论:数值分析 误差插值法与数值微分 数据拟合法快速傅氏变换数值积分第四章快速傅氏变换•三角函数插值•三角插值函数的确定−DFT •FFT算法三角函数插值•已知f (x )在x l =2πl /N ,l =0,1,…,N -1上的值f l =f (x l ) ,l =0,1,…,N -1求满足即l =0,1,…,N -1(1)∑=-==Nj kxk c x 0i 1i ,e )(ϕ∑-===10/i 2e)(N k Nkl k l ll c f f x πϕ三角插值函数的确定−DFT•(1)的解k =0,1,…,N -1(2)(2)和(1)形式相似,分别称有限离散傅氏变换及其逆变换.∑-=-=1/i 2e1N l Nkl l k f Nc π正交性•记则•用e -2jlπi/N 乘(1)两边,对l 求和,交换求和次序,应用上边得到的正交性,就得到(2)式.1,,1,0,e e 1/i )1(2i/210-=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=-N j f f f f N N j N j πj Nπϕ⎩⎨⎧≠====∑∑-=-=--kj kj N N l N l Nl k j Nkl N jl k j ,0,eee),(1010/i )2(i/2/i 2πππϕϕ向量表示•用向量记号(1)即∑∑-=-===11N j jj N k k k c c f ϕϕ∑-=-==1/i 2e1),(1)2(N l Nkl l k k k f Nf N c ,πϕϕ利用正交性乃得作内积与DFT 计算•记k =0,1,…,N -1(3)它代表(1)或(2).(3) 大体上要(复数)N 2个乘法和N 2个加法.但是注意到ω=e ±2πi /N 是N 次单位根,它的幂只有N 个值不同,即1,ω,ω2,…,ωN -1.因此,可用交换律、结合律化简,得到一个只需要N log 2N 个乘法和N log 2N 个加法的算法,FFT .∑∑-=-===101/i 2eN k N k lk l Nkl l k a a c ωπFFT:递推关系N =2m时FFT 可按奇偶项分成两个N /2的FFT 之和.∑∑∑∑-=-=+-=-=+++=+=12/012/02122212/012/0)12(12)2(2)()(N l N l lkl klkl N l N l kl l kl l k aa aa c ωωωωωk =0,1,…,N -1由ωN /2= -1可以对k =N /2,N /2+1,…,N -1采用下式计算12/,,2,1,)()(12/012/021222/2-=-=∑∑-=-=++N k aac N l N l lkl klk lk N ωωω•分而治之FFT:递归算法procedure fft(a,c,n,ω)if n=1c(0)=a(0)elsefor k=0,1,…,n/2-1 {数据奇偶拆分两组}u(k)=a(2k)s(k)=a(2k+1)endfft(u,v,n/2,ω2) {递归FFT调用}fft(s,t,n/2,ω2)for k=0,1,…,n/2-1c(k)=v(k)+ωk t(k) {合成结果数据}c(k+n/2)=v(k)-ωk t(k)endend二进制整数•以N =23=8为例,k,l ≤8•二进制表示k=k 222+k 121+k 020=(k 2k 1k 0)2l=l 222+l 121+l 020=(l 2l 1l 0)2不妨略去括号外下标2.•利用ωN =1可得•(3)可因此表示如次)()0()00(0120112k k k l k k l k l klωωωω=FFT:Cooley-Tukey (N =8))()0()00(1010101280012012001102012]))(([)(k k k l k k l k l l l l l lk l k l l l a a c k k k c ωωωω∑∑∑∑=======∑∑∑=======1)(0102210310)0(010101021)00(012001010120120001221011202)()()()()()()()(l k k k l l k k l l k l l k k Ak k k A l l kA l k k A l l l Al l k A l l l a l l l A ωωω(续)•可见所得A3要按二进制数按位反转的次序重排方得ck•归纳起来,整个过程分四步:由输入数据A0算A1,由A1算A2,由A2算A3,最后按位反转重排得到输出结果ck•还可利用ω0=1,ω4=-1再行简化.•下面整理的公式可供N=2m时编程参考.A 0 、A 1、A 2、A 3•A 1(0l 1l 0)=A 0(0l 1l 0)+A 0(1l 1l 0)A 1(1l 1l 0)=A 0(0l 1l 0)-A 0(1l 1l 0),l 0,l 1=0,1•A 2(k 00l 0)=A 1(k 00l 0)+A 1(k 01l 0)A 2(k 01l 0)=A 1(k 00l 0)-A 1(k 01l 0),k 0,l 0=0,1•A 3(k 0k 10)=A 2(k 0k 10)+A 2(k 0k 11)A 3(k 0k 11)=A 2(k 0k 10)-A 2(k 0k 11),k 0,k 1=0,1)00(0k ω)00(0k ω)0(01k k ω)0(01k k ω计算量与存储量•A1,A2,A3每个数组需复数乘法N/2次,加法N次,共乘法N/2log2N次,加法N log2N次.合计实数乘法2N log2N次,加法3N log2N次.•A1,A2,A3每个数组的分量皆可成对计算,只需几个辅助单元和一个数组A.注意,第二项中ω的幂正好是所算左端量二进下标从红字起往前读三位(前零计入)所表示的数.•N次单位根、二进制数按位反转另行安排.01•A(000)=A0(000)+A0(100)a0=a0+a4 1A1(100)=A0(000)-A0(100)a4=a0-a4 A1(001)=A0(001)+A0(101)a1=a1+a5 A1(101)=A0(001)-A0(101)a5=a1-a5 A1(010)=A0(010)+A0(110)a2=a2+a6 A1(110)=A0(010)-A0(110)a6=a2+a6 A1(011)=A0(011)+A0(111)a3=a3+a7 A1(111)=A0(011)-A0(111)a7=a3-a712•A(000)=A1(000)+A1(010)a0=a0+a22A2(010)=A1(000)-A1(010)a2=a0-a2A2(001)=A1(001)+A1(011)a1=a1+a3A2(011)=A1(001)-A1(011)a3=a1-a3A2(100)=A1(100)+A1(110)ω2a4=a4+a6ω2 A2(110)=A1(100)-A1(110)ω2a6=a4-a6ω2 A2(101)=A1(101)+A1(111)ω2a5=a5+a7ω2 A2(111)=A1(101)-A1(111)ω2a7=a5-a7ω223•A(000)=A2(000)+A2(001)a0=a0+a13A3(001)=A2(000)-A2(001)a1=a0-a1A3(010)=A2(010)+A2(011)ω2a2=a2+a3ω2 A3(011)=A2(010)-A2(011)ω2a3=a2-a3ω2 A3(100)=A2(100)+A2(101)ωa4=a4+a5ωA3(101)=A2(100)-A2(101)ωa5=a4-a5ωA3(110)=A2(110)+A2(111)ω3a6=a6+a7ω3 A3(111)=A2(110)-A2(111)ω3a7=a6-a7ω3按位反转重排•A(000)→c(000)a0→c0 3A3(001)→c(100)a1→c4 A3(010)→c(010)a2→c2 A3(011)→c(110)a3→c6 A3(100)→c(001)a4→c1 A3(101)→c(101)a5→c5 A3(110)→c(011)a6→c3 A3(111)→c(111)a7→c7FFT算法(先按位反转重排) a0→a0a0=a0+a1a0=a0+a2a0=a0+a4a4→a1a1=a0-a1a1=a1+a3ω2a1=a1+a5ωa2→a2a2=a2+a3a2=a0-a2a2=a2+a6ω2a6→a3a3=a2-a3a3=a1-a3ω2a3=a3+a7ω3a1→a4a4=a4+a5a4=a4+a6a4=a0-a4a5→a5a5=a4-a5a5=a5+a7ω2a5=a1-a5ωa3→a6a6=a6+a7a6=a4-a6a6=a2-a6ω2a7→a7a7=a6-a7a7=a5-a7ω2a7=a3-a7ω3FFT算法(续)•所得算法有其特点更易编程先按位反转重排,结果是自然顺序ω的幂递增规律明显每列成对分量间隔r按2的幂递增1,2,…,2m-1. r对分量成一组.共2m-j 组程序如右将原数据按逆序重排,仍记为a k.r = 1for j=1, 2, , mN p=2rθ = –2π/N p= –π/r,w p=exp(iθ)w = 1 初始化for s=0, 1, , r–1 逐对算for k=s,s+N p, , N–1 逐组算l = k + rd = w*a la k= a k +da l= a k –dendw=w*w pendr = N pend。


关于中国古典数学认识刍议记不得什么时候了,在与北京师范大学著名数学教授、数学系原主任严士健先生聊天时,我对他说,对中国古代数学,我们实际上只知道几个点,我们数学史工作者的任务是将“点”串联成“线”,成为数学史。
2009年5月22-25日在北京师范大学召开的第三届数学史与数学教育国际研讨会上,严先生在致辞中谈到了我的上述看法,表示赞同。
十几年来,这种想法一直萦绕于心,却没有时间整理。
今借第26届国际科学史大会中国数学史组召开之机,将这种看法阐述如下,以就教于方家。
一、值得注意的几个现象中国古典数学的成就,特别是其最辉煌的时期,即从公元前2~3世纪至14世纪初的成就,日渐得到国内外有识之士和公正学者的认可。
但是,对中国古典数学,有几个现象值得我们注意。
1.1 西汉至元中叶的大部分数学著作亡佚自先秦到清末现存的数学著作到底有多少,没有精确统计过,有人说是二千余部,有人说是一千余部。
但是无论如何,它们绝大多数产生于明末至清末。
产生于明末以前的仅存三四十部,而成就最大、最辉煌的西汉初至元中叶,只有《周髀筭经》(赵爽注)、张苍耿寿昌编定的《九章筭术》(刘徽注、李淳风等注释)、徐岳的《数术记遗》(甄鸾注)、刘徽的《海岛筭经》(李淳风等注释)、《孙子筭经》、张丘建的《张丘建筭经》(刘孝孙细草)、甄鸾的《五曹筭经》、甄鸾的《五经筭术》、王孝通的《缉古筭经》、赝本《夏侯阳筭经》、《筭学源流》、秦九韶的《数书九章》、李冶的《测圆海镜》、李冶的《益古演段》、杨辉的《详解九章筭法》(存约三分之二,包括贾宪的《黄帝九章筭经细草》)、杨辉的《乘除通变本末》、杨辉的《田亩比类乘除捷法》、杨辉的《续古摘奇筭法》(后三者常合称为《杨辉筭法》)、朱世杰的《筭学启蒙》、朱世杰的《四元玉鉴》等20部传世[1]。
当然,这决不意味着自西汉至元中叶就只出现了这20部数学著作。
二十四史中的艺文志、经籍志列出的数学著作,大部分失传了。
中国古典数学的著述大体分两类,一类是《九章筭术》那样的综合性著作,一类是为《九章筭术》作注[2]。

计算方法引论:微分方程数值解法▪常微分方程初值问题的数值解法▪双曲型方程的差分解法▪抛物型方程的差分解法▪橢圆型方程的差分解法▪有限元方法第十四章椭圆型方程差分解法•差分方程的建立•差分方程组解的存在唯一性问题•收敛性与误差估计Poisson 方程第一边值问题•Poisson 方程第一类边值问题•差分方法问题–选取适当网格,将微分方程离散成差分方程–当网格步长h →0时,差分方程的准确解是否收敛到微分方程的解–解相应的代数方程组2222(,) (,)(,) (,)u uu f x y x y x y u x y x y ΓΩϕΓ⎧∂∂∆=+=∈⎪∂∂⎨⎪=∈⎩建立网格•作平行直线–x=ih, i=0,±1,±2,…,y=kτ, k=0,±1,±2,…–h,τ称为网格的步长–平行线的交点称为节点相邻节点:两节点沿x方向或沿y方向只差一个步长•Γ:全部边界点的集合h–网线与Γ的交点称为边界点. u值已知•Ω:全部内点的集合h–内点:属于Ω的节点.u值未知.正则内点:四个相邻节点均属于Ω∪Γ非正则内点:其它内点差分近似•正则内点差商代替微商•近似解满足差分方程•截断误差=O (h 2+τ2)22(4)22(,)22(4)22(,)(1,)2(,)(1,)(,)12(,1)2(,)(,1)(,)12xxxx i k yyyy i k u u i k u i k u i k h u x j x h uu i k u i k u i k u i y yττ∂+-+-=-∂∂+-+-=-∂,1,,1,,1,,1,2211(2)(2)=h i k i k i k i k i k i k i k i ku u u u u u u f h τ+-+-∆=-++-+22(4)(4)(,)(,)1212xxxx yyyy h R u x j u i y τ=--差分近似(续)•非正则内点–直接转移u Q =u (R )=ϕ(R ) 截断误差为O (h ) –线性插值近似解满足方程截断误差为O (h )•差分方程组–每个内点立一个方程,边界点的值已知,方程的数目与未知数数目相等.PQ u dh h R d h h u +++=)(ϕ差分方程排序•网格节点的联通性–假定是联通的即对任意两个节点,必有一串节点(i =1,2,…,m )可以与P', P"排列成P', P 1, P 2, …, P m , P",使前后两点为相邻节点.•节点排序–把全部节点按一定次序编号,并把i 号节点P i 简写成i ,再用U (i )表示与第i 号节点相邻的所有节点的集合h Ω,h P P Ω'''∈i h P Ω∈差分方程组特性•差分方程组系数–依节点编号次序安排方程和未知数次序得(14.10)–系数满足条件(14.11)–线性方程组,求和号中含u j =ϕj 的项可移到右端,改a ij =0从而d ii <0()h i ii i ij j i hj U i j i ii h u a u a u f i u i ΩϕΓ∈≠⎧∆=+=∈⎪⎨⎪=∈⎩∑0,0,0)(,,,,≤+=Ω∈≥<∑≠∈ij i U j ji i i ii hj i i i aa d j i a a•极值原理假设(1)v i 是定义在网格点上的一组值,.i ∈Ωh +Γh .(2) v i ≠常数. (3) 则v i 不可能在Ωh 上达到正的最大值. 如果将(3)改为则不可能在Ωh 上达到负的最小值•证明用反证法.设v i 在i 0∈Ωh .达到了正的最大值M ,则根据假设(2)及连通性,总可找到这样的.i 0,它有一个相邻节点(相应的系数为正)取值小于M,于是由(14.11)可知这与假设(3)相矛盾. 另一部分结论,证明类似.0.h i ∆≥v 0h i ∆≤v 00h i ∆<v•定理差分方程边值问题(14.10)的解存在唯一.•证明–这只要证明相应的齐次问题只有零解.事实上,由利用极值原理的第一部分可知v i 只能在边界上取正的最大值,但在Γh 上=0,因此v i ≤0, 再应用极值原理的第二部分,知只能在边界上取负的最小值,但在Γh 上v i =0 ,所以必有v i ≥0, 综合上面两个结果,有v i =0, 定理得证0 0 h i h i h i i ΩΓ∆=∈⎧⎨=∈⎩v v 0h i ∆=v比较定理•比较定理假设(1) V i 和v i 是在网格点上给定的两组值.i ∈Ωh +Γh ..(2) 在Ωh 上,V i 和v i 满足关系(3) 在Γh 上,.则在网格区域上,i ∈Ωh +Γh •证明因为在Ωh 上,即或因为在Γh 上有–V i ≤v i ≤V i 即V i –v i ≥0, V i +v i ≥0由极值原理知,在i ∈Ωh +Γh 有V i –v i ≥0, V i + v i ≥0即h i h iV ∆≤-∆v i i V ≥v i i V ≥v h i h i V ∆≤-∆v h i h i h i V V ∆≤∆≤-∆v ()0, ()0h i i h i i V V ∆-≤∆+≤v v i iV ≥v收敛性与误差估计•定理若Poisson 方程第一边值问题解u (x ,y )在Ω+Γ上有四阶连续偏导数,则差分格式(14.10)收敛,且有估计式(14.21):W I =u (i )-u i •证明W i 满足, ︱R h ︱≤Mh 2令它与xOy 平面交于一个包含Ω的圆,圆内Q 非负.由及得(14.21)22211()44i W Mh Q i Mh r ≤≤ 0 h i h h i h W R i W i ΩΓ∆=∈⎧⎨=∈⎩42max ,62M M M ⎛⎫= ⎪⎝⎭22200(,)()()Q x y r x x y y =----()4, h i i h Q Q i Ω∆=∆=-∈221(,), 4h h i h Mh Q x y Mh W i Ω⎛⎫∆=-≤-∆∈ ⎪⎝⎭()0, i hQ i W i Γ≥=∈。


计算方法引论:数值代数⏹解线性方程组的直接法⏹解线性方程组最小二乘问题⏹解线性方程组的迭代法⏹矩阵特征值和特征向量的计算⏹非线性方程及非线性方程组解法第七章线性方程组最小二乘问题•线性最小二乘问题•满秩分解•广义逆矩阵•Gram-Schmidt方法•Householder变换•Givens变换•奇异值分解线性最小二乘问题•线性代数方程组Ax=b(1)–相容:有解, 可能有无穷多解(欠定).–不相容(矛盾,超定):无解.–广义解:最小二乘解.总存在,可能有无穷多.•最小二乘解–求剩余平方和║Ax -b ║2的最小值点–求正规方程(法方程)A T Ax =A T b (通常意义)的解–二者等价:象数据拟合法那样用微分法可得⎪⎪⎩⎪⎪⎨⎧=+++=+++=+++mn mn m m n n n n b x a x a x a b x a x a x a b x a x a x a 22112222212111212111满秩分解与广义逆矩阵•满秩矩阵:A,rank(A)=min{m,n}m×n–行满秩:A,rank(A)=mm×n–列满秩:A,rank(A)=nm×n•满秩分解A= B m×r A r×n,rank(A)=rm×n–(不惟一)可取A的线性无关列为B,它们表出A各列的系数对应为C•广义逆矩阵(惟一)–A+=C T(CC T)-1(B T B)-1B T•注:广义逆矩阵可多个方式定义并确认其惟一性.似乎用奇异值分解更简明实用A+计算•满秩矩阵–行满秩: A+=A T(AA T)-1–列满秩: A+=(A T A)-1A T •非零向量–行向量:x=(x1,x2 ,…,x n)x +=x T/(x12+…+x n2)–列向量x=(x1, x2,…,x n) Tx +=x T/ (x12+…+x n2) •例[][]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=-⨯⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=-⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡--=21211012151112111212211AA +计算又例•A 作满秩分解消元所有列都用1、3列表出131042611713013⎛⎫⎪= ⎪ ⎪⎝⎭A 0.0535710.0178570.0714290.160710.0535710.214290.369050.0119050.380950.422620.0297620.452380.208330.0416670.16667+-⎛⎫⎪- ⎪⎪=-- ⎪- ⎪ ⎪-⎝⎭A 消元矩阵解释•求A +–·–·1–·1131040011100000⎛⎫⎪--⎪ ⎪⎝⎭131040011100111⎛⎫⎪-- ⎪⎪--⎝⎭ ③–②·1 ②–①·2 ③–①·1 1113013210011110⎛⎫⎛⎫⎪=⎪⎪-⎝⎭⎪⎝⎭A 100131042100011111100*********4210011111⎛⎫⎛⎫ ⎪⎪=-- ⎪⎪ ⎪⎪⎝⎭⎝⎭⎛⎫⎛⎫ ⎪= ⎪ ⎪--⎝⎭ ⎪⎝⎭AA+性质•X=A+满足Penrose方程–AXA=A(P1)–XAX=X(P2)–(AX)T=(AX)(P3)–(XA)T=(XA)(P4)•性质–A可逆A+=A-1–(A T)+= (A+)T–(A T A)+=A+(A T)+–(A+A)2=A+A,(AA+)2=AA+•注:不具有逆的某些性质[][]2222))(())((乃知)(1141))(()()()(故2/1)()(,1)(1121)()()(1)(,1121)(,01,11++++++++++++++≠=⎥⎦⎤⎢⎣⎡=≠==⎥⎦⎤⎢⎣⎡==⎥⎦⎤⎢⎣⎡===⎥⎦⎤⎢⎣⎡=xyxyxyxyxyyxyxyxyxxyxyyxyx方程组(1)的解•方程组(1)有解iff AA+b=b–充分性:AA+b=b,则x=A+b满足(1)–必要性:有Ax=b即有AA+(Ax)=b, AA+b=b •(1)有解则其通解为(2)x=A+b+(I-A+A)z, z任意n维向量–(1)有解则A+b是解而A(I-A+A)=A-AA+A=O–设y是解.令z=y-A+b则Az=o.于是z=(I-A+A)z,从而y=A+b+z=A+b+(I-A+A)z.方程组(1)的解(续)•(1)有解时A+b为其通解(2)中惟一2-范数最小者.一般情况下(1)的最小二乘解通解亦(2), A+b仍为其通解中惟一2-范数最小者–(1)有解通解是(2).由于(A+)T(I-A+A)=(A+)T (A+A)T(I-A+A)=(A+)T (A+A-A+A)=O.得║x ║2 = ║A+b║2+║(I-A+A)z║2 +(A+b)T(I-A+A)z= ║A+b║2+║(I-A+A)z║2>0,当(I-A+A)z≠o–一般情况下.令b=c+d, c=AA+b,d=(I-AA+)b,则c T d=0,A T d=o,Ax=c有解y=A+c+(I-A+A)z=A+b+(I-A+A)z,且║b-Ax║2=║c+d-Ax║2 =║c-Ax║2 +║d║2 > ║d║2 ,当Ax≠c.乃证得(1)的最小二乘解通解亦(2).其中A+b为惟一2-范数最小者前己证得.Gram-Schmidt 正交化•G-S 方法可将线性无关的向量组正交化–β1=α1, r 11=║β1║,q 1=β1/r 11–β2=α2-r 12q 1, r 12=(α2, q 1), r 22=║β2║,q 2=β2/r 22–βk =αk -r 1k q 1 -r 2k q 2 -…-r k-1,,k q k , r ik =(αk , q i ), i =1,2, …,k -1, r kk =║βk ║, q k =βk /r kk , k =3, …,n•矩阵表示–A=QR–(α1α2 …αn )=(q 1q 2…q n )⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡nn n n r r r r r r22211111•G-S 方法•修改的G-S 方法–后一算法改变原算法:算出后立即修改使之皆与正交,以后对它们逐个作类似处理.–二算法主要运算量是乘法和加法运算各mn 2次1112/||||=βααfor j = 2:nT T T 112211j j j j j j j --=----βαβαββαββαβ 2/||||j j j =βββ endfor j = 1:n2/||||j j j =βαα for k = j +1:nT k k j k j =-ααβαβ endend1β211,,,n j j j =-:ααααβαβ211,,,2,3,,.n j j j j n =-=:ααααβαβT 211,,,2n j j j j =-=:ααααβαβ1β•A =QR•各列正交化过程5251103202230012---⎛⎫⎪-⎪= ⎪- ⎪-⎝⎭A 0.980580.0377430.176600.0764720.196120.188710.883020.3823600.981310.176600.07647200.397360.91766-⎛⎫⎪-- ⎪= ⎪⎪-⎝⎭Q 5.0990 1.9612 5.49130.588350 2.0381 1.5852 2.528800 2.5166 3.267200.76472---⎛⎫⎪- ⎪=⎪- ⎪⎝⎭R T T 22121(0.076923,0.38462,2,0)=-=-βαβαβ22|||| 2.0381=βT 2(0.037743,0.18871,0.98131,0)=-βT T13235.4913, 1.5852=-=βαβαT T T33131232(0.44444,2.2222,0.44444,1)=--=-βαβαββαβ32|||| 2.5166=βT3(0.17660,0.88302,0.17660,0.39736)=-β-3.2672T4(0.058480,0.29240,0.058480,0.70175)=---β42||||0.76472=βT4(0.076472,0.38236,0.076472,0.91766)=--β12|||| 5.0990=αT1(0.98058,0.19612,0,0)=βT 12 1.9612=-βαT T T 1424340.58835, 2.5288,0.32672=-=-=-βαβαβαHouseholder 变换•定义–H =I -2ww T , ║ w ║ =1•性质–H T =H–H T H =H 2=I–任一x ,║Hx ║=║x ║–任给x 及y ,║y ║=║x ║≠0,总有H 使Hx=y , 不难验证:取w =(x-y )/ ║x-y ║即可.–y 常取坐标轴方向,如y = -sign(x 1 )║x ║ e 1v =x +sign(x 1)║x ║ e 1(w =v / ║v ║)H =I -βvv T ,β=2/v T v用此变换可将矩阵化成上三角(消元)Household变换:算法•变换Hx= -αe1:计算v(存入x)及α=sign(x1)║x║,β–η=max{|xi|}计算v及β时引入的比例因子–xi=x i/η, 1≤i≤n–α= sign(x1)║x║–x1=x1+α, β =(αx1)-1, α= ηα•计算A=HA(H由β,v给出)–设A=(a1… aq)则HA=A-βvv T A=(…a j -βvv T a j…)–算法:对j=1,2,…,qσ=v T aja j =a j -σβv•由此不难导出化上三角的算法Household 正交化•Householder 变换可实现QR 分解–A =QR , Q m ×m 正交阵, R m ×n 上三角阵–实现:作Q p …Q 2Q 1A=R , Q k 是H-变换.p =min{m -1,n }, 即得A =QR , Q =Q 1Q 2…Q p -1•典型步(对照右边矩阵表示)–象消元法那样将右下角矩阵第一列对角元下全变成零(己是则免,H =I )–Ĥ=I -βvv T ,β=2/v T v同前,H =diag(I Ĥ)也是H-变换T⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡*=⎥⎦⎤⎢⎣⎡*⎥⎦⎤⎢⎣⎡v o v o I H A o r A H A O R H I β•Householder 正交化(QR 分解)算法1.输入m n ⨯∈A R ,置1,min(1,).k p m n ==- 2.max(||,,1,,).ik a i k k m η==+ 3.若0η=,则0,0k kk d r ==,否则221/,,,sign()(),1,,,,,,1,,ik ik kk kkmkkk kk k kk kk m j ik ij k i k ij ij j ik a a i k ma a a a a d a r a a d j k n a a a i k m j k n ηαααηαττ-====++=+==-⎛⎫==+ ⎪⎝⎭=-==+∑ 4.若k <p ,则k = k +1,转步骤2;否则,结束. 11213111(1)(2)2223222(1)(2)(3)333333(1)(2)(3)444,,r r r r r r βββ⎛⎫ ⎪⎛⎫⎛⎫ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎪⎝⎭A r d v v v v v v v v v (1)11213(1)(2)2223(1)(2)(3)333(1)(2)(3)444,r r r ⎛⎫ ⎪⎛ ⎪==⎪⎪⎝ ⎪⎝⎭A r v v v v v v v v v 运算量:乘、加各次求Q=H 1…H P I 另需乘、加次数各存储方式: 2313mn n -22312()3m n mn n -+2.0198 1.9612 5.49130.588350.20.39223 1.9652 2.157302230012⎛⎫ ⎪- ⎪ ⎪- ⎪-⎝⎭•A =QR•正交化过程k = 1525110320223012---⎛⎫⎪-⎪= ⎪- ⎪-⎝⎭A 5.0990 1.9612 5.49130.588350 2.0381 1.5852 2.528800 2.51663.2672000.76472-⎛⎫⎪-- ⎪= ⎪-⎪-⎝⎭R 0.980580.0377430.176600.0764720.196120.188710.883020.3823600.981310.176600.076472000.397360.91766---⎛⎫⎪-- ⎪= ⎪---⎪-⎝⎭Q a 1 = (5,1,0,0)T ,5η= 1.0198α=T11(2.0198,0.2,0,0)==a v 11110.48548, 5.0990d r β===-a 1 = (1,0.2,0,0)T ,a 11 =1+1.098= 2.019 8用以变换A 的后三列得到1Household 正交化算例(续)•正交化过程k = 2•正交化过程k = 3T2(0.39223,2,0),2η==a 220.19612 1.0190 1.2152a =+=T22(1.2152,1,0)==a v 22220.80755, 2.0381d r β===-2.0198 1.9612 5.49130.588350.2 1.2152 1.5852 2.528801 2.3094 2.6943012⎛⎫⎪- ⎪⎪- ⎪-⎝⎭用以变换A 的最后一列得到用以变换A 的后二列得到T3(2.3094,1), 2.3094η==a T3(1,0.43301)=a 1.0897α=T33(2.0897,0.43301)==a v 33330.43913, 2.5166d r β===-2.01981.9612 5.49130.588350.21.2152 1.58522.528801 2.08973.2672000.433010.76472⎛⎫ ⎪- ⎪ ⎪⎪-⎝⎭T2(0.19612,1,0), 1.0190α==a T 11T 22T330.48548,(2.0198,0.2,0,0)0.80755,(1.2152,1,0)0.43913,(2.0897,0.43301)βββ======v v v R 如前,Q 可由下面的信息生成Givens 变换•定义–G =G (i ,k ,θ)=I +s (e i e k T -e k e i T )+c (e i e i T +e k e k T )•性质–G T G =I–任给x 可使y =G x 的k 分量为零:r =(x i 2+x k 2)1/2 ≠0c =x i /r ,s =x k /r•可用以化上三角形一如消元过程⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-=11),,(c s s c k i G θendend ,11, else ,11, if else 0,1 0 if 22cts tc x x t stc ts x x t x x s c x i k k i ik k =+===+==≥===Givens 正交化算例•算例•过程525110320223012---⎛⎫⎪-⎪= ⎪- ⎪-⎝⎭A 0.980580.0377430.176600.0764720.196120.188710.883020.3823600.981310.176600.076472000.397360.91766--⎛⎫⎪- ⎪=⎪-⎪⎝⎭Q 5.09901.9612 5.49130.5883502.0381 1.5852 2.528800 2.51663.267200.76472---⎛⎫⎪- ⎪=⎪- ⎪-⎝⎭R (2,1)元变为零,t = 0.2, c = 0.980 58, s = 0.196 12.一行:5.099 0 –1.961 2 –5.491 3 –0.588 35二行:0 0.392 23 –1.961 2 2.157 3(3,2)元变零,t = 0.196 12, c = 0.192 45, s = 0.981 31.二行:0 2.038 1 1.585 2 –2.528 8三行:0 0 2.309 4 –2.694 3(4,3)元变零,t = 0.433 01, c = 0.917 66, s = 0.397 36.QR 分解定理•定理设A 是m ×n (m ≥ n ) 矩阵,则A 有QR 分解, 其中Q 是m ×n 的正交矩阵,R 是具有非负对角元的上三角矩阵;而且当m = n 且A 非奇异时R 的对角元皆正上述分解还是唯一的•证⎛⎫= ⎪⎝⎭R A Q O 于是,有T 12T11||||⎛⎫= ⎪ ⎪⎝⎭Q A A v α 1 n –1对(1)(1)m n -⨯-矩阵A 1应用数学归纳法假定,得 212⎛⎫= ⎪⎝⎭R A Q O 其中,Q 2是(m –1)×(m –1)正交矩阵,R 2是具有非负对角元的(1)(1)n n -⨯-上三角矩阵. 这样,令T 121221||||,⎛⎫⎛⎫== ⎪ ⎪ ⎪⎝⎭⎝⎭Q Q R Q R αv 000 则Q 和R 满足定理的要求. 存在性得证.再证唯一性. 设m = n 且A 非奇异,易知R 对角元皆正,假定==A QR QR ,其中,Q , Q 是m m ⨯正交矩阵,R , R 是具有正对角元的上三角矩阵. A 非奇异蕴含着R , R 的对角元均为正数,因此,有 T 1-=Q Q RR 既是正交矩阵又是对角元均为正数的上三角矩阵,只能是单位矩阵. 从而,必有=Q Q ,=R R 即分解是唯一的先证存在性,用数学归纳法. 当n = 1时,定理显然成立. 现假定已经对所有p ×(n –1)矩阵成立,这里假设(1)p n ≥-,设m n ⨯矩阵A 的第一列为1α(可为零向量),则由定理7.5知,存在m m ⨯正交矩阵Q 1,使得T 11121||||=Q e αα于是,有T 12T11||||⎛⎫=⎪ ⎪⎝⎭0Q A A v α 1 n –1 对(1)(1)m n -⨯-矩阵A 1应用数学归纳法假定,得212⎛⎫= ⎪⎝⎭R A Q O 1m –1最小二乘解:列满秩•列满秩时求(1)的最小二乘解–形成正规方程A T Ax=A T b(n阶)(乘法和加法各mn2/2次) 用平方根法(乘法和加法各n3/6次)用G-S作A=QR:R T Rx=R T Q T b,Rx=Q T b(各mn2次) –用Householder变换或Givens变换作QR分解║Ax-b║2 =║Q T Ax-Q T b║2==║Rx-c1║2+║c2║2,解x=R-1c1,最小值║c2║2注: 若记Qm×m =(Q1 Q2), Q1是m×n阵则有c1=Q1b,c2=Q2b⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡21ccxOR最小二乘解:列满秩算例•求最小二乘解•求最小二乘解L123525110320223012x x x ---⎛⎫⎛⎫⎛⎫ ⎪ ⎪- ⎪ ⎪ ⎪= ⎪ ⎪ ⎪- ⎪ ⎪ ⎪⎝⎭-⎝⎭⎝⎭12326102831081442814399x x x ---⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪-=- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭正规方程5.0190001.9912 2.038105.4913 1.58522.5166⎛⎫⎪- ⎪⎪-⎝⎭T( 1.6023,0.23099, 1.2982)=---x 5.09901.9612 5.49130.5883502.0381 1.5852 2.528800 2.51663.26720000.76472-⎛⎫ ⎪-- ⎪=⎪- ⎪-⎝⎭R 5251103202230012---⎛⎫ ⎪- ⎪= ⎪- ⎪-⎝⎭A 方程H-正交化增广矩阵T ( 1.6023,0.23099, 1.2982)=---x 剩余是0.764 721.9612奇异值分解(SVD)•矩阵奇异值–A m ×n 的奇异值σ1≥σ2≥…≥σr >σr+1=…=σn =0是A T A 的特征值λ1, …,λn 的平方根•奇异值分解定理),,diag(正交阵,1Tr n n m m σσΣV U V O O O ΣU A =⎥⎦⎤⎢⎣⎡=⨯⨯形式阵即得矩,,1,连同,得,,,1由),,,(阵 正交增.则,,1,/令,,),,,(证.取TTT21T TT21分解補成r k u Av o Av o Av A v o Av A n r k u u u U u u r k Av u v Av A I V V v v v V k k k k k kk m kj j k k k k k k k n =====+========σδσλ奇异值分解(续)•推论(记号同前)–分解形式A=σ1u1v1T+σ2u2v2T+…+σr u r v r TA=ÛΣŴT, Û=(u1u2…u r),Ŵ =(v1v2…v r)–空间关系R(A)=Span{u1,u2,…,u r}N(A)=Span{v r+1,v r+2,…,v n}R(A T)=Span{v1,v2,…,v r}N(A T)=Span{u r+1,u r+2,…,u m}R(A)=N(A T)⊥, R(A T)=N(A)⊥SVD 与A+•X =A +满足Penrose 方程–AXA =A (P1)–XAX =X (P2)–(AX )T =(AX )(P3)–(XA )T =(XA )(P4)•由SVD 解出X =A +T T 111T111rr ru v u v UO O O ΣV A σσ++=⎥⎦⎤⎢⎣⎡=-+T 11T:乃得唯一解得(P4)代入得(P3)代入得(P2)代入得(P1)代入对应分块SVD 解.取U O OO ΣV X O L O K K L ΣM ΣS U M L K S V X ⎥⎦⎤⎢⎣⎡=====⎥⎦⎤⎢⎣⎡=--图示A与A+•SVD绐出A与A+在标准正交基下向量对应关系V1= Span{v,v2,…,v r}, V2= Span{v r+1,v r+2,…,v n},1U1= Span{u,u2,…,u r}, U2=Span{u r+1,u r+2,…,u m}1最小二乘解•(1)的最小二乘解–推导:按前述标准正交基分解,再求║Ax-b║2最小x=c1v1+c2v2+…+c n v nA x=c1σ1u1+c2σ2u2+…+c rσr u rb=u1T b u1+u2T b u2+…+u m T bu m║Ax-b║2最小:c=u k T b/σk,k≤r,其余任意k–最小二乘解通解x=1/σ1u1T b v1+1/σ2u2T b v2+…+1/σr u r T b v r+ v r +…+c n v n, c r+1, …, c n任意c r+1–最小2-范数最小二乘解y=1/σ1u1T b v1+1/σ2u2T b v2+…+1/σr u r T b v rSVD与最小二乘解•上述结果亦可借助SVD得到–A, A+代入通解(2)x=A+b+(I-A+A)z(z任意n维向量)2-范数最小A+b=(1/σ1v1u1T+…+1/σr v r u r T)b(I-A+A)z=(I-(v1v1T+v2v2T+…+v r v r T) )z=(v r+1v r+1T+…+v n v n T)z =c r+1v r+…+c n v n –由SVD直接推出最小二乘解║Ax-b║2=║UΛV T x-b║2=║ΛV T x-U T b║2=║Λc-U T b║2 ,这里Λ=diag(ΣO),c=V T x的i,U T b的i分量u i T b.从而可得结果.分量ci代入正规方程A T Ax=A T b关于A +的定义•A +有多个等价定义–由满秩分解:C T (CC T )-1(B T B )-1B T–由Penrose 方程.–由SVD:–由最小二乘解:(1)中任一b 对应唯一最小2-范数最小二乘解x 所确定的矩阵.–由线性算子确定的矩阵.线性算子f :R m →R nf (y )=x ,当y ∈R (A ), Ax =y f (y )=o ,当y ⊥R (A )•注.一个或几个Penrose 方程可定义多种广义逆T1V O O O ΣU ⎥⎦⎤⎢⎣⎡-。
课程号:20100440 课程名:泛函分析课程英文名:Functional Analysis学时:68 学分:4先修课程:实变函数、高等代数基本面向:数学学院教材:《泛函分析》江泽坚、孙善利编高等教育出版社1998 一版参考书:1.《实变函数与泛函分析》(下册)夏道行等等教育出版社1984 一版2.《实变函数与泛函分析》(下册)曹广福、严从荃编人民教育出版社第2版3. W.Rudin,Functional Analysis,McGraw_HillBook Company,1973课程简介:线性赋范空间,Banach空间,Hilbert空间(包括有界,紧集,列紧集,完全有界集等)。
Banach 空间上有界线性算子(包括算子范数,有界性,连续性,Hahn-Banach定理,闭图象定理,逆算子定理,谱理论,紧算子Riesz-Schauder理论等)Hilbert 空间上的有界线性算子(射影定理、Riesz表示定理)。
课程号:20100640 课程名:概率统计课程英文名Probability and Statistics学时:68 学分:4先修课程:数学分析、线性代数基本面向:数学学院各专业教材:《概率论基础》(第二版)李贤平高等教育出版社1997参考书:1.《概率论》(第一册概率论基础)复旦大学高等教育出版社,1979。
2.《概率论引论》汪仁官北京大学出版社19943.《概率论及数理统计》(第二版)(上)梁之舜等高等教育出版社1988课程简介:事件与概率,条件概率与统计独立性,随机变量与分布函数,数字特征与特征函数,极限定理。
课程号:20100850 课程名:高等代数-1课程英文名:Advanced Algebra-1学时:102 学分:5先修课程:高中数学基本面向:数学数院各专业教材:《Advanced Algebra》彭国华、李德琅高等教育出版社-Springer(计划2004年出版参考书:1。
《高等代数》北京大学数学系几何代数教研空编高等教育出版社2.《高等代数》张禾瑞、郝锅新高等教育出版社3.《Linear Slgebra》B。
数值计算方法的书
以下是一些数值计算方法的书籍:
《数值计算方法》(作者:徐萃薇、孙绳武):这本书是数值计算方法的
经典教材,详细介绍了数值计算的基本概念和方法,包括插值、数值积分、非线性方程的求解、数值微分等。
《数值分析》(作者:李庆扬、王能超、易大义):这本书是数值分析的
经典教材,详细介绍了各种数值计算算法和技术,包括线性方程组、矩阵特征值、插值和逼近、数值积分等。
《实用数值分析》(作者:苏煜城、吴勃英):这本书是一本实用的数值
分析教材,主要面向工程技术人员,介绍了各种数值计算方法的应用和实现。
此外,还有《数值分析基础》、《计算物理基础教程》等书可供选择。
可以根据自己的需求和兴趣选择合适的书籍进行学习。
计算⽅法引论课后答案.第⼀章误差1. 试举例,说明什么是模型误差,什么是⽅法误差.解: 例如,把地球近似看为⼀个标准球体,利⽤公式24A r π=计算其表⾯积,这个近似看为球体的过程产⽣的误差即为模型误差.在计算过程中,要⽤到π,我们利⽤⽆穷乘积公式计算π的值:12222...q q π=?其中112,3,...n q q n +?=??==?? 我们取前9项的乘积作为π的近似值,得3.141587725...π≈这个去掉π的⽆穷乘积公式中第9项后的部分产⽣的误差就是⽅法误差,也成为截断误差.2. 按照四舍五⼊的原则,将下列各数舍成五位有效数字:816.956 7 6.000 015 17.322 50 1.235 651 93.182 13 0.015 236 23 解: 816.96 6.000 0 17.323 1.235 7 93.182 0.015 236 3. 下列各数是按照四舍五⼊原则得到的近似数,它们各有⼏位有效数字? 81.897 0.008 13 6.320 05 0.180 0 解: 五位三位六位四位4. 若1/4⽤0.25表⽰,问有多少位有效数字? 解: 两位5. 若 1.1062,0.947a b ==,是经过舍⼊后得到的近似值,问:,a b a b +?各有⼏位有效数字?解: 已知4311d 10,d 1022a b --()433211110100.551010222d a b da db da db ----+=+≤+=?+?=?所以a b +有三位有效数字;因为0.1047571410a b ?=?,()43321110.94710 1.1062100.600451010222所以a b ?有三位有效数字.6. 设120.9863,0.0062y y ==,是经过舍⼊后作为12,x x 的近似值.求1211,y y 的计算值与真值的相对误差限及12y y ?与真值的相对误差限. 解: 已知-4-41112221211d ,d ,d =10,d 1022x y x x y x x x =+=+?=?, ()44111111110d d 12dr dr 0.50100.9863x xx x x y --==≈=≈? ???;()42222222110d d 12dr dr 0.81100.0062x xx x x y --==≈=≈? ???;()()()4221212dr dr dr 0.50100.81100.8210x x x x ---?=+≈?+?≈?.7. 正⽅形的边长约为100cm,应该怎样测量,才能使其⾯积的误差不超过1cm 2.解: 设正⽅形⾯积为S,边长为a,则S=a 2.所以要使:2d d 2d 1s a a a ==≤,则要求211d 0.5102200a a -≤==?.所以边长的误差不能超过20.510-?cm.8. ⽤观测恒星的⽅法求得某地维度为4502'''o(读到秒),试问:计算sin ?将有多⼤误差?解: ()()1d sin cos d cos 45022*''?'''==o.9 . 真空中⾃由落体运动距离s 与时间的关系由公式212s gt =确定,g 是重⼒加速度.现在假设g 是准确的,⽽对t 的测量有0.1s ±的误差,证明t 增加时,距离的绝对误差增加⽽相对误差却减⼩.证明: 因为:221d d d d d d d ;2.122s gt t gt t t s gt gt t s s t gt ??d s 与t 成正⽐,d s s与t 成反⽐,所以当d t 固定的时候, t 增加时,距离的绝对误差增加⽽相对误差却减⼩.10. 设0x >,x 的相对误差为δ,求ln x 的绝对误差. 解: 已知d x x δ=,所以ln x 的绝对误差()d d ln x x x δ==.11. 设x 的相对误差为%α,求nx 的相对误差.解: 1d d d %n n n n x nx x n xn x x xα-===.12. 计算球的体积,为了使相对误差限为1%,问度量半径R 时允许的相对误差限如何? 解: 已知34 3V R π=,设()d dr R R a R ==,则要使得 ()()3d dr dln d ln 3d ln 3d ln 3dr 31%V V V R R R R a V ========,则11%3a =?.第⼆章插值法与数值微分1.设y =在100,121,144x =三处的值是很容易求得的,试以这三个点建⽴y =的⼆次插值多项式,,且给出误差估计.⽤其中的任意两点,构造线性插值函数,⽤得到的三个线性插值函数,,并分析其结果不同的原因.解: 已知012012100,121,144;10,11,12x x x y y y ======,建⽴⼆次Lagrange 插值函数可得:()()()()21211441001441011100121100144121100121144121100 12144121144100x x x x L x x x ----= +------+--()211510.7228L ≈=.误差()()()()()()2012012,,,,3!f R x x x x x x x x x x ξξξ'''=---∈,所以20.00065550.001631R <<利⽤前两个节点建⽴线性插值函数可得:()()()()()11211001011100121121100x x L x --=+--()111510.7143L ≈=.利⽤后两个节点建⽴线性插值可得:()()()()()11441211112121144144121x x L x --=+--()111510.7391L ≈=.利⽤前后两个节点建⽴线性插值可得:()()()()()21441001012100144144100x x L x --=+()111510.6818L ≈=.,⼆次插值⽐线性插值效果好,利⽤前两个节点的线性插值⽐其他两个线性插值效果好.此说明,⼆次插值⽐线性插值效果好,插⽐外插效果好.2. 利⽤(2.9)式证明()()()0121001max ,8x x x x x R x f x x x x ≤≤-''≤≤≤证明: 由(2.9)式()()()()0101,2!f R x x x x x x x ξξ''=--<<当01x x x <<时,()()01max x x x f f x ξ≤≤''''≤,()()()01201101max 4x x x x x x x x x ≤≤--≤- 所以()()()0121001max ,8x x x x x R x f x x x x ≤≤-''≤≤≤3. 若()0,1,...,j x n 为互异节点,且有()()()()()()()()()011011............j j n j jj j j j j n x x x x x x x x l x xx x x x x x x -+-+----=证明()0,0,1,...,nk kj j j x l x xk n =≡=∑证明: 由于() 1 ;0 .j i ij i j l x i j δ=?==?≠? 且()0nk j j j x l x =∑和kx都为k 次多项式,⽽且在k+1个不同的节点处的函数值都相同0,1,...,k n =, 所以马上有()0,0,1,...,nk kj j j x l x xk n =≡=∑.4. 设给出sin x 在[],ππ-上的数值表,⽤⼆次插值进⾏计算,若希望截断误差⼩于5 10-,问函数表的步长最⼤能取多少? 解: 记插值函数为p(x),则()()()()()11sin sin 3!i i i x p x x x x x x x ξ-+'''-=--- 所以()()()()11cos max sin 3!i i i x x p x x x x x x ππξ-+-≤≤--=---()()()[]3112,0,2i g x th h t t t t -+=--∈⼜()()()[]12,0,2t t t t t ?=--∈的最⼤值为10.3849??= ?,所以有 350.3849max sin 106x x p h ππ--≤≤-≤< 所以 0.0538h ≤.5. ⽤拉格朗⽇插值和⽜顿插值找经过点()()()()3,1,0,2,3,2,6,10---的三次插值公式. 解: Lagrange 插值函数:()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()12302330101020310121301301223202123303132 31033101622731033 .2781/5x x x x x x x x x x x x L x y y x x x x x x x x x x x x x x x x x x x x x x x x y y x x x x x x x x x x x x x x x x x x x x x x x x ------= +------------++--------+--=++-+-++⽜顿插值: ⾸先计算差商3 10 2 13 2 1.333 0.38896 104 0.8889 0.1420-----()()()()()3130.38893 1.142033.N x x x x x x x =-++-+++-也可以利⽤等距节点构造,⾸先计算差分。
第二章 插值法知识点:拉格朗日插值法,牛顿插值法,余项,分段插值。
实际问题中,时常不能给出f (x )的解析表达式或f (x )解析表达式过于复杂而难于计算,能采集的只是一些f (x )的离散点值{xi,f(xi)}(i=0,1,2,…n )。
因之,考虑近似方法成为自然之选。
定义:设f (x )为定义在区间[a ,b]上的函数,x0,x1,…,xn 为[a ,b]上的互异点,yi=f (xi )。
若存在一个简单函数ϕ(x ),满足(插值条件)ϕ(xi )=f (xi ),i=0,1,…,n 。
则称 ϕ(x )为f (x )插值函数,f (x )为被插函数,点x0,x1,…,xn 为插值节点,点{xi,f(xi)},i=0,1,2,…n 为插值点。
于是计算f (x )的问题就转换为计算 ϕ(x )。
构造插值函数需要解决:插值函数是否存在唯一;插值函数如何构造(L 插值);插值函数与被插函数的误差估计和收敛性。
对插值函数 ϕ(x )类型有多种不同的选择,代数多项式常被选作插值函数。
P23(2.18)和(2.19)指出,存在唯一的满足插值条件的n 次插值多项式p n (x )。
但是需要计算范德蒙行列式,构造插值多项式工作量过大,简单表达式不易得到,实际中不采用这类方法。
插值法是一种古老的数学方法,拉格朗日(Lagrange )、牛顿(Newton )等分别给出了不同的解决方法。
拉格朗日插值拉格朗日(Lagrange )插值的基本思想:把插值多项式p n (x )的构造问题转化为n+1个插值基函数l i (x)(i=0,1,…,n)的构造。
(1)线性插值 ①构造插值函数已知函数y =f (x )的两个插值点(x 0,y 0),(x 1,y 1),构造多项式y =p 1(x ),使p 1(x 0)=y 0,p 1(x 1)=y 1。
p n (x )≈f (x )由直线两点式可知,通过A ,B 的直线方程为 变形为 记 则p 1(x )=l 0(x )y 0+l 1(x )y 1插值完毕!注意性质:l 0(x 0)=l 1(x 1)=1,l 0(x 1)=l 1(x 0)=0,p 1(x 0)=y 0,p 1(x 1)=y 1。
称l 0(x ),l 1(x )为点x 0、x 1的线性插值基函数。
插值函数p 1(x )是这两个插值基函数的线性组合,这种形式的插值称作为拉格朗日(Lagrange )插值,相应多项式称拉格朗日线性插值多项式,记作L 1(x )。
②误差设L 1(x )为插值点(x 0,y 0),(x 1,y 1)的插值函数,f(x0)= y 0,f(x0)=y 1,f(x)一阶连续可导,二导数存在.则对任意给定的x ∈[a,b],存在一点ξ∈[a,b],使引进辅助函数,利用洛尔定理即证,见P17定理2.1。
(2)二次插值 ①构造插值函数给定三个点{xi,f(xi)}, i=0,1,2,其中xi 互不相同,构造函数f (x )的二次插值多项式L 2(x ),满足:L2(x 0)=y 0,L 2(x 1)=y 1,L 2(x 2)=y 2。
通过三点的插值问题称为二次插值或抛物插值。
仿线性插值,用插值基函数构造插值多项式。
令L 2(x )=l 0(x )y 0+l 1(x )y 1+l 2(x )y 2待定函数l i (x )应是二次函数,满足约束条件l i (xi )=1,l i (xj )=0(i ≠j ),i ,j =0,1,2。
此设l 0(x )=A(x-x1)(x-x2),l 1(x )=B(x-x0)(x-x2),l 2(x )=C(x-x0)(x-x1)。
根据约束条件确定系数 由此得 ②误差( ) ) ( 1 0 01 0 1 0 x p x x x x y y y y = - - - = +1A = (x 0-x 1)(x 0-x 2)1C = (x 2-x 0)(x 2-x 1)1B = (x 1-x 0)(x 1-x 2)L 2(x) =(x-x 1)(x-x 2) (x 0-x 1)(x 0-x 2) f(x 0) (x-x 0)(x-x 2) (x 1-x 0)(x 0-x 2) 1) (x-x 0)(x-x 1) (x 2-x 0)(x 2-x 1)2)+ + R 2(x) =(x-x 0)(x-x 1)(x-x 2) f (ξ) (3),ξ∈[Min{x 0,x 1, x 2,x}, Min{x 0,x 1, x 2,x}] R 1(x) =(x-x 0)(x-x 1) f (ξ) (2)2!,ξ∈[a,b] f(x)-L 1(x) = x-x 1p 1(x )= x 0-x 1 + x-x 0 x 1-x 0 y 0 y 1 x-x 1l 0(x ) =x 0-x 1x-x 0l 1(x )= x 1-x 0证明见P22定理2.2。
例 设sin11°=0.190809,sin12°=0.207912。
用线性插值计算sin11°30ˊ. 解L 1(11.5)=0.199361例 设sin11°=0.190809,sin12°=0.207912,sin13°=0.224951。
用二次插值计算sin11°30ˊ 解L 2(11.5)=0.199369.(3)一般情况两个插值点可求出一次插值多项式L 1(x ),而三个插值点可求出二次插值多项式L 2(x )。
当插值点增加到n +1个时,利用Lagrange 插值方法写出n 次插值多项式L n (x )。
详细说明见P22-24,(2.20),(2.21)至(2.24)。
关于Langrange 插值的几点说明L n (x )仅与已知数据(x i ,y i ),(i =0,1,…,n) 有关,与f(x)的原来形式无关,但余式与f(x)密切相关。
若f(x)本身是一个不超过n 次多项式,则内插(x 位于x0,x1,…,xn 之间)误差较小,外插有可能误差变大,慎用!插值点的增减,基函数要重新计算,很不方便!插值节点过多其精度不一定很好;limL n (x )=f (x ),x ∈[a,b]一般不成立.knk nk nkj j jk jkk n y x x x x x l y x L ) ( ) ( ) ( 0∑ ∑ ∏= = ≠ = - - = =x-12 L 1(x ) =11-12 x-110.190809 + 12-110.207912 R 1(x) = (x-x 0)(x-x 1) f (ξ) (2)2!=(x-11)(x-12) -Sin(ξ) 2! |R 1(11.5)| ≢|(11.5-11)(11.5-12)|=0.125 12L 2(x) = (x-12)(x-13) (11-12)(11-13) (x-11)(x-13) (12-11)(12-13) 0.207912 (x-11)(x-x 12) (13-11)13-12)0.224951 + +) ( ) ( , 0 ) ( x f x L x R nn ≡ = 即第二章 插值法知识点:拉格朗日插值法,牛顿插值法,余项,分段插值。
Newton 插值法Lagrange 插值多项式的一个缺点是没有承袭性质,增加插值节点时,需要重新计算所有插值基函数。
牛顿插值多项式克服了这一缺点:增加一个节点时,可在原插值多项式基础上增加一项构成高一阶的插值多项式。
(1)差商即其性质证 采用数学归纳法即证性质2差商与节点排列顺序无关。
(2)线性牛顿插值设互异y 0=f (x 0),y 1=f (x 1),构造线性插值函数的牛顿格式N 1(x )使y 0= N 1 (x 0),y 1= N 1 (x 1)。
利用点斜式,构造N 1(x )=a 0+a 1(x-x 0) 由f (x 0)=N 1 (x 0)= a 0f (x 1)= N 1 (x 1)= f (x 0) +a 1(x 1-x 0得N 1 (x )= f (x 0) +(x-x 0) (3)二次牛顿插值上的二在节点定义 设函数 y=f(x) 在区间 [ a , b ] 上 n +1 个互异节点 0 { x j } n处的值 为: y i = f(x i ) ( i =0,1,2, …,n ) - ① 称 ji j i j i x x x f x f x x f - ∆) () ( ] , [ 为 f(x) 在节点 x i, 上的一阶差商;② 称 ki k j j i k j i x x x x f x x f x x x f -- ∆ ] , [ ] , [ ] , , [ 为 在节点 阶差商 ; 依次类推 :③ 称 nn n n x x x x x f x x x f x x x f - - ∆- 0 2 1 1 1 0 1 0 ],..., , [ ] ,... , [ ] ,..., , [ 为 上的 n 阶差商.x j f(x) x k x j, x i, f(x)x 0, x 1, …, x n ))....( )( ( ) ( ) () ( ] ,..., , [ ) ,..., 2 , 1 , 0 ( ) ( ] ,..., , [ 1 1 0 0 ' 1 0 1 0 n nj j j nj n x x x x x x x x x f x x x f n j x f x x x f n - - - = = = ∑ = ω ω 其中 的线性组合,即 函数值 是阶差商 性质 ] , [ 1 0 x x f ) ( ) ( 01 0 1] , [ 1 0 x x f x x x f x f = - - a 1=设互异y 0=f (x 0),y 1=f (x 1), y 2=f (x 2),构造二次牛顿插值多项式N 2(x )使y 0= N 2(x 0),y 1= N 2(x 1),y 2=N 2(x 2)。
令N 2(x )=a 0+a 1(x-x 0) +a 2(x-x 0) (x-x 1)因在构造N 1 (x )过程中已得a 0和a 1,只要求出a 2即可 由f (x 2)=N 2(x 2)= f (x 0) + (x 2-x 0)+a 2(x 2-x 0)(x 2-x 1得N 2(x 2)= f (x 0) + (x 2-x 0)+ (x 2-x 0)(x 2-x 1)(4)一般情况设互异y i =f (x i ),i=0,1,…,n 。
构造n 次牛顿插值多项式N n (x )使y i = N n (x i ),i=0,1,…,n,。
根据差商定义分段插值(1)高阶插值与龙格现象构造插值多项式时,根据误差表达式,是否多取插值点比少取插值点好?不一定!若被插函数是多项式,则多取插值点比少取插值点好。