专题突破练5 专题一 常考小题点过关检测

专项一过关检测(45分钟,100分)【一】选择题(本大题共20小题,每题3分,共60分。

在每题列出的四个选项中,只有一项为哪一项符合题目要求的)1观察以下图,结合所学知识,判断与以下图无关的是()。

A.与中国历史上第一次思想解放运动有关B.他们之间的关系是诘难、批驳,同时吸收、融合C.当时的学派只有这【五】六家,号称〝百家〞D.〝学在民间〞促成这种现象的出现解析:〝百家〞是个概数,具体的数字很难确定,故当时学派只有【五】六家的说法显然是不正确的。

答案:C2韩非在批评某家学说时说:〝举先王,言仁义者盈廷,而政不免于乱。

〞他批评的是()。

A.法家学说B.道家学说C.儒家学说D.墨家学说解析:题目的着眼点是题干中的材料提到的韩非批评的〝言仁义者盈廷〞,因为儒家思想的核心是〝仁〞,由此可以判断答案为C项。

答案:C32019年是孔子诞辰2561年,上海世博会山东馆设计推出高2.561米的铸铜贴金孔子雕像,辅以由39句«论语»经典名句设计的文字浮雕墙,以〝孔子厚德仁爱的文化胸怀铸造城市灵魂〞提升了展示内涵。

下面四句话中,你认为不能被选为上海世博会山东馆开篇序语的是()。

A.〝有朋自远方来,不亦乐乎〞B.〝四海之内皆兄弟也〞C.〝君子和而不同〞D.〝非礼勿视,非礼勿听,非礼勿言,非礼勿行〞解析:此题考查准确理解历史问题的能力。

D项重在维护统治秩序,不利于社会和谐。

答案:D4电视剧«老大的幸福»播出后,曾引发了一场关于幸福的大讨论,老大〝拿自己的短处和别人的长处比,越比越憋屈;拿自己的长处和别人的短处比,越比越幸福〞的观点表达了一种〝知足常乐〞的洒脱。

与之最为接近的思想是()。

A.孟子〝民贵君轻〞的儒家思想B.老子〝清静无为〞的道家思想C.韩非〝严刑峻法〞的法家思想D.荀子〝人之性恶〞的儒家思想解析:此题考查分析理解能力。

〝知足常乐〞即不过多追求难以得到的东西,不做无谓的攀比,形象的表现就是剧中人老大的幸福观,〝拿自己的短处和别人的长处比,越比越憋屈;拿自己的长处和别人的短处比,越比越幸福〞。

专题突破练5 专题一常考小题点过关检测一、单项选择题1.(2020全国Ⅰ,理2)设集合A={x|x2-4≤0},B={x|2x+a≤0},且A∩B={x|-2≤x≤1},则a=()A.-4B.-2C.2D.42.(2020山东淄博4月模拟,2)命题“∃x0∈(0,+∞),ln x0=x0-1”的否定是()A.∀x∈(0,+∞),ln x≠x-1B.∀x∉(0,+∞),ln x=x-1C.∃x0∈(0,+∞),ln x0≠x0-1D.∃x0∉(0,+∞),ln x0=x0-13.(2020全国Ⅲ,理2)复数11-3i的虚部是()A.-310B.-110C.110D.3104.(2020天津,2)设a∈R,则“a>1”是“a2>a”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.(2020山东模考卷,2)已知a+b i(a,b∈R)和1-i1+i是共轭复数,则a+b=()A.-1B.-12C.12D.16.(2020山西太原二模,理5)若a,b是两个非零向量,且|a+b|=m|a|=m|b|,m∈[1,√3].则向量b与a-b夹角的取值范围是()A.[π3,2π3] B.[π3,5π6]C.[2π3,5π6] D.[5π6,π]7.(2020山东济南一模,5)方舱医院的创设,在抗击新冠肺炎疫情中发挥了不可替代的重要作用.某方舱医院医疗小组有七名护士,每名护士从周一到周日轮流安排一个夜班.若甲的夜班比丙晚一天,丁的夜班比戊晚两天,乙的夜班比庚早三天,己的夜班在周四,且恰好在乙和丙的正中间,则周五值夜班的护士为()A.甲B.丙C.戊D.庚8.关于x的方程x2+(m-3)x+m=0在(0,2)内有两个不相等实数根,则实数m的取值范围是()A.(23,1]B.(23,1) C.(1,3)D.(-∞,1)∪(9,+∞) 二、多项选择题9.已知x<-1,那么在下列不等式中成立的是( ) A.x 2-1>0 B.x+1x <-2 C.sin x-x>0D.cos x+x>010.若1a <1b <0,则下列不等式成立的是( ) A.1a+b <1ab B.|a|+b>0 C.a-1a>b-1bD.ln a 2>ln b 211.(2020海南天一大联考模拟三,9)设a ,b ,c 为实数且a>b ,则下列不等式一定成立的是( ) A.1a>1bB.2 020a-b >1C.ln a>ln bD.a (c 2+1)>b (c 2+1)12.(2020山东历城二中模拟四,10)已知a ,b 是单位向量,且a +b =(1,-1),则( ) A.|a +b |=2 B.a 与b 垂直 C.a 与a -b 的夹角为π4 D.|a -b |=1 三、填空题13.(2020全国Ⅰ,文14)设向量a =(1,-1),b =(m+1,2m-4),若a ⊥b ,则m= . 14.(2020天津河北区线上测试,15)已知a>0,b>0,且1a+1b =1,则1a -1+4b -1的最小值为 .15.(2020山东济宁6月模拟,14)在平行四边形ABCD 中,AD=6,AB=3,∠DAB=60°,DE ⃗⃗⃗⃗⃗ =12EC ⃗⃗⃗⃗⃗ ,BF ⃗⃗⃗⃗⃗ =12FC ⃗⃗⃗⃗⃗ ,若FG ⃗⃗⃗⃗⃗ =2GE ⃗⃗⃗⃗⃗ ,则AG ⃗⃗⃗⃗⃗ ·BD⃗⃗⃗⃗⃗⃗ = .16.已知f (x )=x 2+2x+1+a ,∀x ∈R ,f (f (x ))≥0恒成立,则实数a 的取值范围为 .专题突破练5 专题一 常考小题点过关检测1.B 解析由已知得A={x|-2≤x ≤2},B={x |x ≤-a2}.因为A ∩B={x|-2≤x ≤1},所以有-a2=1,解得a=-2. 2.A 解析因为已知的是特称命题,所以它的否定为全称命题,故选A . 3.D 解析∵11-3i =1+3i(1-3i )(1+3i )=1+3i 10=110+310i,∴复数11-3i 的虚部是310.4.A 解析若a>1,则a 2>a 成立.若a 2>a ,则a>1或a<0.故“a>1”是“a 2>a ”的充分不必要条件.故选A . 5.D 解析由1-i 1+i=(1-i )22=-2i 2=-i,得a+b i =-(-i)=i,所以a=0,b=1,所以a+b=1.6.C 解析根据题意,设|a |=|b |=t ,则|a+b |=mt ,再设向量b 与a-b 夹角为θ,则有|a+b |2=(a+b )2=a 2+b 2+2a ·b =m 2t 2,变形可得a ·b =m 2t 22-t 2, 则有|a-b |2=(a-b )2=a 2+b 2-2a ·b =2t 2-2(m 2t 22-t 2)=4t 2-m 2t 2,则cos θ=b ·(a -b )|b ||a -b |=a ·b -b 2|b ||a -b |=m 2t 22-t 2-t 22=1222=-12×√4-m 2.由1≤m ≤√3,得1≤√4-m 2≤√3,则有-√32≤cos θ≤-12.又由0≤θ≤π,得2π3≤θ≤5π6,即θ的取值范围为[2π3,5π6].故选C .7.D 解析因为己的夜班在周四,且恰好在乙和丙的正中间,所以乙可能在星期一,二,三,五,六,日.因为乙的夜班比庚早三天,所以乙可能在星期二,三.如果乙在星期三,则庚在周六,且丙在周五,庚比丙晚一天,但与甲的夜班比丙晚一天矛盾,则乙在周二,庚在周五.故选D .8.B 解析由题意,令f (x )=x 2+(m-3)x+m ,则{Δ=(m -3)2-4m >0,f (0)=m >0,f (2)=4+2(m -3)+m >0,0<-m -32<2,解得23<m<1,故选B . 9.ABC 解析由x<-1,得|x|>1,所以x 2>1,即x 2-1>0,故A 成立;因为x<-1,所以-x>1,0<-1x <1,所以(-x )+(-1x )>2,即x+1x <-2,故B 成立; 因为x<-1,而sin x ∈[-1,1],即sin x>x ,所以sin x-x>0,故C 成立; 因为x<-1,而cos x ∈[-1,1],所以cos x+x<0,故D 不成立.故选ABC . 10.AC 解析由1a <1b <0,可知b<a<0.因为a+b<0,ab>0,所以1a+b<0,1ab >0,故有1a+b<1a θ,故A 正确;因为b<a<0,所以-b>-a>0,故-b>|a|,即|a|+b<0,故B 错误; 因为b<a<0,又有1a <1b <0,则-1a >-1b >0,所以a-1a >b-1b ,故C 正确;因为b<a<0,根据y=x 2在(-∞,0)上为减函数,可得b 2>a 2>0,而y=ln x 在定义域(0,+∞)上为增函数,所以ln b 2>ln a 2,故D 错误.故选AC .11.BD 解析对于A,若a>b>0,则1a <1b ,故A 错误;对于B,因为a-b>0,所以2020a-b >1,故B 正确;对于C,函数y=ln x 的定义域为(0,+∞),而a ,b 不一定是正数,故C 错误;对于D,因为c 2+1>0,所以a (c 2+1)>b (c 2+1),故D 正确.12.BC 解析由a+b =(1,-1)两边平方,得|a |2+|b |2+2a ·b =12+(-1)2=2,则|a+b |=√2.因为a ,b 是单位向量,所以1+1+2a ·b =2,得a ·b =0,则|a-b |2=a 2+b 2-2a ·b=2,所以|a-b|=√2,所以cos <a ,a-b >=a ·(a -b )|a ||a -b |=21×√2=√2=√22,所以a 与a-b 的夹角为π4.13.5 解析由a ⊥b ,可得a ·b =1×(m+1)+(-1)×(2m-4)=0,解得m=5. 14.4 解析∵a>0,b>0,且1a +1b=1,∴a>1,b>1,且b=aa -1,∴1a -1+4b -1=1a -1+4aa -1-1=1a -1+4(a-1)≥2√1a -1·4(a -1)=4,当且仅当a=32时,等号成立.∴1a -1+4b -1的最小值为4.15.21 解析以A 为原点,AD 为x 轴,AD 的垂线为y 轴,建立如图所示的平面直角坐标系,则A (0,0),B (32,3√32),D (6,0),F 72,3√32,E132,√32.设点G 的坐标为(x ,y ).∵FG ⃗⃗⃗⃗⃗ =2GE ⃗⃗⃗⃗⃗ ,∴x-72,y-3√32=2132-x ,√32-y ,解得x=112,y=5√36,∴G (112,5√36).∴AG ⃗⃗⃗⃗⃗ ·BD⃗⃗⃗⃗⃗⃗ =112,5√36·92,-3√32=994−15×312=21.16.[√5-32,+∞) 解析设t=f (x )=(x+1)2+a ≥a ,∴f (t )≥0对任意t ≥a 恒成立,即(t+1)2+a ≥0对任意t ∈[a ,+∞)都成立.当a ≤-1时,f (t )min =f (-1)=a , 即a ≥0,这与a ≤-1矛盾;当a>-1时,f (t )min =f (a )=a 2+3a+1,则a 2+3a+1≥0,解得a ≥√5-32.。

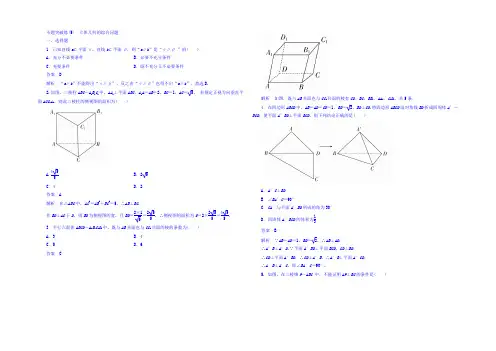
专题突破练(5) 立体几何的综合问题 一、选择题1．已知直线a ⊂平面α，直线b ⊂平面β，则“a ∥b ”是“α∥β ”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分又不必要条件答案 D解析 “a ∥b ”不能得出“α∥β”，反之由“α∥β”也得不出“a ∥b ”．故选D.2.如图，三棱柱ABC －A 1B 1C 1中，AA 1⊥平面ABC ，A 1A ＝AB ＝2，BC ＝1，AC ＝5， 若规定正视方向垂直平面ACC 1A 1，则此三棱柱的侧视图的面积为( )A.455B ．2 5C ．4D ．2答案 A解析 在△ABC 中，AC 2＝AB 2＋BC 2＝5，∴AB ⊥BC .作BD ⊥AC 于D ，则BD 为侧视图的宽，且BD ＝2×15＝255，∴侧视图的面积为S ＝2×255＝455.3．平行六面体ABCD －A 1B 1C 1D 1中，既与AB 共面也与CC 1共面的棱的条数为( ) A ．3 B ．4 C ．5 D ．6答案 C解析 如图，既与AB 共面也与CC 1共面的棱有CD 、BC 、BB 1、AA 1、C 1D 1，共5条．4．在四边形ABCD 中，AB ＝AD ＝CD ＝1，BD ＝2，BD ⊥CD .将四边形ABCD 沿对角线BD 折成四周体A ′－BCD ，使平面A ′BD ⊥平面BCD ，则下列结论正确的是( )A ．A ′C ⊥BDB ．∠BA ′C ＝90°C ．CA ′与平面A ′BD 所成的角为30° D ．四周体A ′BCD 的体积为13答案 B解析 ∵AB ＝AD ＝1，BD ＝2，∴AB ⊥AD . ∴A ′B ⊥A ′D .∵平面A ′BD ⊥平面BCD ，CD ⊥BD ， ∴CD ⊥平面A ′BD ，∴CD ⊥A ′B ，∴A ′B ⊥平面A ′CD ， ∴A ′B ⊥A ′C ，即∠BA ′C ＝90°.5. 如图，在三棱锥P －ABC 中，不能证明AP ⊥BC 的条件是( )A．AP⊥PB，AP⊥PCB．AP⊥PB，BC⊥PBC．平面BPC⊥平面APC，BC⊥PCD．AP⊥平面PBC答案 B解析由AP⊥PB，AP⊥PC可推出AP⊥平面PBC，∴AP⊥BC，故排解A；由平面BPC⊥平面APC，BC⊥PC 可推出BC⊥平面APC，∴AP⊥BC，故排解C；由AP⊥平面PBC可推出AP⊥BC，故排解D，选B.6．如图所示，已知在多面体ABC－DEFG中，AB，AC，AD两两垂直，平面ABC∥平面DEFG，平面BEF∥平面ADGC，AB＝AD＝DG＝2，AC＝EF＝1，则该多面体的体积为( )A．2 B．4C．6 D．8答案 B解析如图所示，将多面体补成棱长为2的正方体，那么明显所求的多面体的体积即为该正方体体积的一半，于是所求几何体的体积为V ＝12×23＝4.7．设A，B，C，D是半径为2的球面上的四点，且满足AB⊥AC，AD⊥AC，AB⊥AD，则S△ABC＋S△ABD＋S△ACD 的最大值是( )A．6 B．7C．8 D．9答案 C解析由题意知42＝AB2＋AC2＋AD2，S△ABC＋S△ACD＋S△ABD＝12(AB·AC＋AC·AD＋AD·AB)≤12⎣⎢⎡12AB2＋AC2＋12AC2＋AD2＋⎦⎥⎤12AD2＋AB2＝12(AB2＋AC2＋AD2)＝8.8．已知圆锥的底面半径为R，高为3R，在它的全部内接圆柱中，表面积的最大值是( )A．22πR2 B.94πR2C.83πR2 D.52πR2答案 B解析如图所示，为组合体的轴截面，记BO1的长度为x，由相像三角形的比例关系，得PO13R＝xR，则PO1＝3x，圆柱的高为3R－3x，所以圆柱的表面积为S＝2πx2＋2πx·(3R－3x)＝－4πx2＋6πRx，则当x＝34R 时，S取最大值，S max＝94πR2.9．在正方体ABCD－A1B1C1D1中，P为正方形A1B1C1D1四边上的动点，O为底面正方形ABCD的中心，M，N 分别为AB，BC边的中点，点Q为平面ABCD内一点，线段D1Q与OP相互平分，则满足MQ→＝λMN→的实数λ的值有( )A ．0个B ．1个C ．2个D ．3个 答案 C解析 本题可以转化为在MN 上找点Q 使OQ 綊PD 1，可知只有Q 点与M ，N 重合时满足条件，所以选C. 10．四棱锥M －ABCD 的底面ABCD 是边长为6的正方形，若|MA |＋|MB |＝10，则三棱锥A －BCM 的体积的最大值是( )A ．16B ．20C ．24D ．28答案 C解析 ∵三棱锥A －BCM 体积＝三棱锥M －ABC 的体积，又正方形ABCD 的边长为6，S △ABC ＝12×6×6＝18，又空间一动点M 满足|MA |＋|MB |＝10，M 点的轨迹是椭球，当|MA |＝|MB |时，M 点到AB 距离最大，h ＝52－32＝4，∴三棱锥M －ABC 的体积的最大值为V ＝13S △ABC h ＝13×18×4＝24，∴三棱锥A －BCM 体积的最大值为24，故答案为C.11．在一个棱长为4的正方体内，最多能放入的直径为1的球的个数( ) A ．64 B ．66 C ．68 D ．70答案 B解析 依据球体的特点，最多应当是放5层，第一层能放16个；第2层放在每4个小球中间的空隙，共放9个；第3层连续往空隙放，可放16个；第4层同第2层放9个；第5层同第1、3层能放16个，所以最多可以放入小球的个数：16＋9＋16＋9＋16＝66(个)，故答案为B.12．如图所示，正方体ABCD －A ′B ′C ′D ′的棱长为1，E ，F 分别是棱AA ′，CC ′的中点，过直线E ，F 的平面分别与棱BB ′、DD ′交于M ，N ，设BM ＝x ，x ∈，给出以下四个命题：①平面MENF ⊥平面BDD ′B ′；②当且仅当x ＝12时，四边形MENF 的面积最小；③四边形MENF 周长L ＝f (x )，x ∈是单调函数； ④四棱锥C ′－MENF 的体积V ＝h (x )为常函数．以上命题中假命题的序号为( ) A ．①④ B ．② C ．③ D ．③④答案 C解析 ①连接BD ，B ′D ′，则由正方体的性质可知EF ⊥平面BDD ′B ′，所以平面MENF ⊥平面BDD ′B ′，所以①正确．②连接MN ，由于EF ⊥平面BDD ′B ′，所以EF ⊥MN ，四边形MENF 的对角线EF 是固定的，所以要使面积最小，则只需MN 的长度最小即可，此时当M 为棱的中点时，即x ＝12时，此时MN 长度最小，对应四边形MENF 的面积最小，所以②正确．③由于EF ⊥MN ，所以四边形MENF 是菱形．当x ∈⎣⎢⎡⎦⎥⎤0，12时，EM 的长度由大变小，当x ∈⎣⎢⎡⎦⎥⎤12，1时，EM 的长度由小变大，所以函数L ＝f (x )不单调，所以③错误．④连接C ′E ，C ′M ，C ′N ，则四棱锥分割为两个小三棱锥，它们以C ′EF 为底，以M ，N 分别为顶点的两个小棱锥．由于三角形C′EF的面积是常数．M，N到平面C′EF的距离是常数，所以四棱锥C′－MENF的体积V＝h(x)为常函数，所以④正确．所以四个命题中③假命题，选C.二、填空题13．如图，在正方体ABCD－A1B1C1D1中，P为棱DC的中点，则D1P与BC1所在直线所成角的余弦值等于________．答案10 5解析连接AD1，AP，则∠AD1P就是所求的角．设AB＝2，则AP＝D1P＝5，AD1＝22，∴cos∠AD1P＝10 5.14.如图，已知球O的面上有四点A、B、C、D，DA⊥平面ABC，AB⊥BC，DA＝AB＝BC＝2，则球O的体积等于________．答案6π解析如图，以DA，AB，BC为棱长构造正方体，设正方体的外接球球O的半径为R，则正方体的体对角线长即为球O的直径，所以|CD|＝22＋22＋22＝2R，所以R＝62，故球O的体积V＝4πR33＝6π.15. 如图，有一圆柱开口容器(下表面封闭)，其轴截面是边长为2的正方形，P是BC的中点，现有一只蚂蚁位于外壁A处，内壁P处有一粒米，则这只蚂蚁取得米粒的所经过的最短路程是________．答案π2＋9解析由于圆柱的侧面开放图为矩形(如图所示)，则这只蚂蚁取得米粒所经过的最短路程应为AQ＋PQ，设点E与点A关于直线CD对称，由于两点之间线段最短，所以Q为PE与CD的交点时有最小值，即最小值为EP＝π2＋9.16．棱长为a的正方体ABCD－A1B1C1D1中，若与D1B平行的平面截正方体所得的截面面积为S，则S的取值范围是________．答案⎝⎛⎭⎪⎫0，6a22解析 如图，过D 1B 的平面为BMD 1N ，其中M ，N 分别是AA 1，CC 1的中点，由于BD 1＝3a ，MN ＝AC ＝2a ，AC ⊥BD 1，即MN ⊥D 1B ，所以过D 1B 与M ，N 的截面的面积为S ＝12AC ·BD ＝62a 2，因此S 的取值范围是⎝⎛⎭⎪⎫0，6a 22.三、解答题17．在边长为4的菱形ABCD 中，∠DCB ＝60°，点E ，F 分别是边CD 和CB 的中点，AC 交BD 于点H ，AC 交EF 于点O ，沿EF 将△CEF 翻折到△PEF 的位置，使平面PEF ⊥平面ABD ，得到如图所示的五棱锥P －ABFED .(1)求证：BD ⊥PA ；(2)求点D 到平面PBF 的距离．解 (1)证明：由于四边形ABCD 为菱形，所以AC ⊥BD . 由于EF 为△BCD 的中位线，所以EF ∥BD ， 故AC ⊥EF ，即翻折后PO ⊥EF .由于平面PEF ⊥平面ABD ，平面PEF ∩平面ABD ＝EF ，PO ⊂平面PEF ，所以PO ⊥平面ABD . 由于BD ⊂平面ABD ，所以PO ⊥BD .又AO ⊥BD ，AO ∩PO ＝O ，AO ⊂平面APO ，PO ⊂平面APO ，所以BD ⊥平面APO . 由于AP ⊂平面APO ，所以BD ⊥PA .(2)连接PC ，由于四边形ABCD 为菱形，且∠DCB ＝60°，故∠ADC ＝120°，AD ＝4，AC ＝43，BD ＝4， S △BDF ＝12S △BDC ＝12×12×4×23＝23，OP ＝14AC ＝ 3.由于PF ＝BF ＝FC ，故△BPC 为直角三角形，∠BPC ＝90°，PC ＝OC 2＋OP 2＝6，PB ＝BC 2－PC 2＝10，S △PBF ＝12S △BPC ＝12×12PB ·PC ＝152. 由于V D －PBF ＝V P －BDF ，所以13h D ·S △PBF ＝13OP ·S △BDF ，所以h D ＝OP ·S △BDF S △PBF ＝3×23152＝4155. 故点D 到平面PBF 的距离为4155.18．如图，在四棱锥P －ABCD 中，底面ABCD 是正方形，点E 是棱PC 的中点，平面ABE 与棱PD 交于点F .(1)求证：AB ∥EF ；(2)若PA ＝AD ，且平面PAD ⊥平面ABCD ，试证明：AF ⊥平面PCD ；(3)在(2)的条件下，线段PB 上是否存在点M ，使得EM ⊥平面PCD ？(直接给出结论，不需要说明理由) 解 (1)证明：由于底面ABCD 是正方形，所以AB ∥CD . 又由于AB ⊄平面PCD ，CD ⊂平面PCD ，所以AB ∥平面PCD .又由于A ，B ，E ，F 四点共面，且平面ABEF ∩平面PCD ＝EF ，所以AB ∥EF . (2)证明：在正方形ABCD 中，CD ⊥AD .又由于平面PAD ⊥平面ABCD ，且平面PAD ∩平面ABCD ＝AD ，所以CD ⊥平面PAD . 又由于AF ⊂平面PAD ，所以CD ⊥AF .由(1)知AB ∥EF ，又由于AB ∥CD ，所以CD ∥EF . 由点E 是棱PC 的中点，可知点F 是棱PD 的中点．在△PAD 中，由于PA ＝AD ，所以AF ⊥PD ，又由于PD ∩CD ＝D ，所以AF ⊥平面PCD . (3)不存在．19．一个多面体的直观图和三视图如下：(其中M ，N 分别是AF ，BC 中点) (1)求证：MN ∥平面CDEF ； (2)求多面体A －CDEF 的体积．解 (1)证明：由三视图知该多面体是底面为直角三角形的直三棱柱，且AB ＝BC ＝BF ＝2，DE ＝CF ＝22，∠CBF ＝90°.取BF 中点G ，连接MG ，NG ，由于M ，N 分别是AF ，BC 中点，则NG ∥CF ，∵MG ∥AB ，又∵AB ∥EF ，∴MG ∥EF ，∴面MNG ∥面CDEF ，∴MN ∥面CDEF .(2)作AH ⊥DE 于H ，由于三棱柱ADE －BCF 为直三棱柱，∴AH ⊥面DCEF ，且AH ＝2， ∴V A －CDEF ＝13S CDEF ·AH ＝13×2×22×2＝83.20. 如图，在四棱锥P －ABCD 中，PD ⊥底面ABCD ，底面ABCD 是直角梯形，AB ∥DC ，AB ⊥AD ，AB ＝3，CD ＝2，PD ＝AD ＝5，E 是PD 上一点．(1)若PB ∥平面ACE ，求PE ED的值；(2)若E 是PD 中点，过点E 作平面α∥平面PBC ，平面α与棱PA 交于F ，求三棱锥P －CEF 的体积． 解 (1)连接BD 交AC 于O ，在△PBD 中，过O 作OE ∥BP 交PD 于E ，∵OE ⊂平面ACE ，PB ⊄平面ACE ， ∴PB ∥平面ACE ，∵AB ＝3，CD ＝2，∴AB CD ＝BO DO ＝PE ED ＝32.(2)过E 作EM ∥PC 交CD 于M ，过M 作MN ∥BC 交AB 于N ， 则平面EMN 即为平面α，则平面α与平面PAB 的交线与PB 平行，即过N 作NF ∥PB 交PA 于F ， ∵E 是PD 的中点，CD ＝2，∴CM ＝1，则BN ＝CM ＝1， 又AB ＝3，∴AN NB ＝2，则FA FP＝2，∵PD ＝AD ＝5，∴F 到平面PCE 的距离为53，则V P －CEF ＝V F －PCE ＝2518.。

专题05 二氧化碳的制取考点扫描☆聚焦中考二氧化碳的制取，是每年中考的必考内容之一，考查的知识点包括制取二氧化碳的装置、药品、原理、步骤、收集、验满、检验、注意事项等；以实验探究题为主。

也有少量选择题。

结合近年全国各地中考的实例，我们从二个方面进行二氧化碳制取问题的探讨：（1）选择题；（2）实验探究题；考点梳理☆温习理解一、制取气体的装置1（1）选择依据：反应物状态、反应条件。

（2）类型：①固液不加热如A；②固固加热如B；（1）选择依据：密度、溶解性、是否发生反应。

收集装置：①排水法：条件：不溶于水且不与水反应；（2）类型：优点：收集的气体纯净；缺点：收集的气体不干燥②向上排空气：条件：密度比空气大且不与空气反应。

优点：收集的气体干燥；缺点：收集的气体不纯净向下排空气：条件：密度比空气小且不与空气反应。

优点：收集的气体干燥；缺点：收集的气体不纯净二、实验室制取二氧化碳（1）药品：大理石或石灰石和稀盐酸；（2）原理：CaCO3+2HCl=CaCl2+H2O+CO2↑；（3）装置：固液不加热，向上排空法，（4）步骤：①连接装置；②检查装置的气密性；③向锥形瓶中加入大理石；④从长颈漏斗加入稀盐酸；⑤收集二氧化碳；⑥验满。

（5）收集法：向上排空气法：原因密度比空气大且不与空气反应；能溶于水，不能用排水法。

（6）验满：向上排空气法，用燃着的木条放在，瓶口，木条熄灭则收集满。

（7）检验：将气体通入澄清石灰水，若石灰水浑浊，则是二氧化碳。

原理：Ca(OH)2+CO2 =CaCO3↓+H2O；（8）注意事项：①长颈漏斗的下端要伸到液面以下（防止产生的气体从长颈漏斗口逸出）；②锥形瓶中的导管只能刚刚露出橡皮塞（有利于产生的气体排出）；③集气瓶中的导管口要接近集气瓶底（目的：便于排净空气）。

（9）药品的选择：①实验室制取二氧化碳不能用稀硫酸和大理石反应是因为（稀硫酸和大理石反应生成的硫酸钙微溶于水，会附着在大理石表面，阻碍反应的继续发生）。

2023年中考数学总复习一轮讲练测（浙江专用）专题25圆的有关计算（讲练）1.理解弧长计算公式的推导过程，掌握弧长公式并能熟练应用于计算；2.理解扇形面积公式的推导过程，掌握扇形面积计算公式并能熟练应用于计算；3.了解正多边形的概念及正多边形与圆的关系；4.能运用图形割补、等积变形等方法将不规则图形转化为规则图形求面积.一．选择题（共7小题）1．（2022•台州）一个垃圾填埋场，它在地面上的形状为长80m，宽60m的矩形，有污水从该矩形的四周边界向外渗透了3m，则该垃圾填埋场外围受污染土地的面积为（）A．（840+6π）m2B．（840+9π）m2C．840m2D．876m22．（2022•丽水）某仿古墙上原有一个矩形的门洞，现要将它改为一个圆弧形的门洞，圆弧所在的圆外接于矩形，如图．已知矩形的宽为2m，高为2m，则改建后门洞的圆弧长是（）A．m B．m C．m D．（+2）m3．（2022•宁波）已知圆锥的底面半径为4cm，母线长为6cm，则圆锥的侧面积为（）A．36πcm2B．24πcm2C．16πcm2D．12πcm24．（2021•衢州）已知扇形的半径为6，圆心角为150°，则它的面积是（）A．πB．3πC．5πD．15π5．（2021•湖州）如图，已知在矩形ABCD中，AB＝1，BC＝，点P是AD边上的一个动点，连接BP，点C关于直线BP的对称点为C1，当点P运动时，点C1也随之运动．若点P从点A运动到点D，则线段CC1扫过的区域的面积是（）A．πB．π+C．D．2π6．（2021•绍兴）如图，正方形ABCD内接于⊙O，点P在上，则∠BPC的度数为（）A．30°B．45°C．60°D．90°7．（2019•湖州）如图，已知正五边形ABCDE内接于⊙O，连接BD，则∠ABD的度数是（）A．60°B．70°C．72°D．144°二．填空题（共2小题）8．（2022•温州）若扇形的圆心角为120°，半径为，则它的弧长为．9．（2018•温州）小明发现相机快门打开过程中，光圈大小变化如图1所示，于是他绘制了如图2所示的图形．图2中六个形状大小都相同的四边形围成一个圆的内接正六边形和一个小正六边形，若PQ所在的直线经过点M，PB＝5cm，小正六边形的面积为cm2，则该圆的半径为cm．三．解答题（共3小题）10．（2022•衢州）如图，C，D是以AB为直径的半圆上的两点，∠CAB＝∠DBA，连结BC，CD．（1）求证：CD∥AB．（2）若AB＝4，∠ACD＝30°，求阴影部分的面积．11．（2020•浙江）如图，的半径OA＝2，OC⊥AB于点C，∠AOC＝60°．（1）求弦AB的长．（2）求的长．12．（2022•金华）如图1，正五边形ABCDE内接于⊙O，阅读以下作图过程，并回答下列问题：作法如图2．1．作直径AF．2．以F为圆心，FO为半径作圆弧，与⊙O交于点M，N．3．连结AM，MN，NA．（1）求∠ABC的度数．（2）△AMN是正三角形吗？请说明理由．（3）从点A 开始，以DN 长为半径，在⊙O 上依次截取点，再依次连结这些分点，得到正n 边形，求n 的值．1．圆的周长公式：C ＝ (半径为R )．圆的面积公式：S ＝ (半径为R )．2．在半径为R 的圆中，n °的圆心角所对的弧长l 的计算公式为：l ＝ ．在半径为R 的圆中，n °的圆心角所对的扇形(弧长为l )面积的计算公式为：S 扇形＝ ＝12lR . 3．圆柱的侧面展开图是 ，这个 的长和宽分别是底面圆的 和圆柱的 ．圆柱侧面积公式：S圆柱侧＝ ；圆柱全面积公式：S 圆柱全＝ (其中圆柱的底面半径为r ，高为h )．4．圆锥的侧面积和全面积：圆锥的侧面展开图是一个扇形，若圆锥的母线长为l ，底面半径为r ，则这个扇形的半径为l ，扇形的弧长为2πr ．(1)圆锥的侧面积公式：S 圆锥侧＝ ．(2)圆锥的全面积公式：S 圆锥全＝ ．(3)圆锥侧面展开图扇形的圆心角度数的计算公式：θ＝ ．5．正多边形的中心：正多边形的外接圆的圆心．外接圆的半径叫做正多边形的 ，正多边形每一边所对的 叫做正多边形的中心角，中心到正多边形的一边的距离叫做正多边形的边心距．作相等的 就可以等分圆周，从而得到相应正多边形．6．不规则图形面积的计算求与圆有关的不规则图形的面积时,最基本的思想就是转化思想,即把所求的不规则的图形的面积转化为规则图形的面积.常用的方法有:(1)直接用公式求解.(2)将所求面积分割后,利用规则图形的面积求解.(3)将阴影中某些图形等积变形后移位,重组成规则图形求解.(4)将所求面积分割后,利用旋转,将部分阴影图形移位后,组成规则图形求解.考点一、正多边形与圆例1（2022•大名县校级四模）如图1所示的正六边形（记为“图形P1”）边长为6，将每条边三等分，沿每个顶点相邻的两个等分点连线剪下6个小三角形（如图1中6个阴影部分的三角形），把剪下的这6个小三角形拼接成图2外轮廓所示的正六边形（记为“图形P2”），作出图形P2的内切圆⊙O，如图3，得到如下结论：①图1中剩余的多边形（即空白部分）为正十二边形；②把图2中空白部分记作“图形P3”，则图形P1，P2，P3的周长之比为3：2：；③图3中正六边形的边上任意一点到⊙O上任意一点的最大距离为4+．以上结论正确的是（）A．②③B．①③C．②D．①【变式训练】1．（2022•顺平县校级模拟）已知，如图，⊙O的半径为6，正六边形ABCDEF与⊙O相切于点C、F，则的长度是（）A．2πB．3πC．4πD．5π2．（2022•亭湖区校级三模）已知正六边形的边长为4，则这个正六边形的半径为（）A．4B．2C．2D．43．（2022•丛台区校级模拟）如图，点P是正六边形ABCDEF内部一个动点，AB＝3cm，则点P到这个正六边形六条边的距离之和为（）cm．A．18B．C．9D．4．（2022•峄城区校级模拟）如图⊙O是正方形ABCD的内切圆，四边形DEFG是矩形，点F在⊙O上，ED ＝8cm，EF＝4cm，则⊙O的半径为（）A．4B．4或20C．20D．5或165．（2022•凤泉区校级一模）如图，在平面直角坐标系中，正六边形ABCDEF的边AB在x轴正半轴上，顶点F在y轴正半轴上，AB＝2．将正六边形ABCDEF绕原点O顺时针旋转，每次旋转90°，经过第2022次旋转后，顶点D的坐标为（）A．（﹣3，﹣2）B．（﹣2．﹣2）C．（﹣3，﹣3）D．（﹣2，﹣3）考点二、弧长的计算例2（2022•丹东模拟）在平行四边形ABCD中，∠B＝70°，BC＝4，以AD为直径的⊙O交CD于点E，则的长是（）A．B．C．D．【变式训练】1．（2022•峄城区校级模拟）若扇形的圆心角为75°，半径为12，则该扇形的弧长为（）A．2πB．4πC．5πD．6π2．（2022•新平县校级模拟）如图，AB是⊙O的直径，点D为⊙O上一点，且∠ABD＝30°，BO＝4，则劣弧的长为（）A．πB．2πC．πD．π3．（2023•汉阳区校级一模）如图，AB是⊙O的直径，C是⊙O上一点，AC＝8，BC＝6，CD平分∠ACB交⊙O于点D，则劣弧AD的长为（）A．πB．πC．2πD．π4．（2022•兴平市模拟）如图，△ABC内接于⨀O，CD⊥AB于点D，若CD＝BD，⨀O的半径为4，则劣弧的长为（）A．5πB．4πC．3πD．2π5．（2022•潍坊三模）如图，在Rt△ABC中，∠BAC＝90°，AB＝6，AC＝8，D为BC的中点，连接AD，以点D为圆心，DA长为半径作弧MN，若DM⊥AB于点E，DN⊥AC于点F．则图中阴影部分的周长为（）A．B．C．D．考点三、扇形面积的计算例3（2022•金凤区校级二模）如图，⊙O内有一个正方形，且正方形的各顶点在圆上，⊙O的半径为2，以点A为圆心，以AC长为半径画弧交AB的延长线于点E，交AD的延长线于点F，则图中阴影部分的面积为（）A．8π﹣8B．8π﹣4C．4π﹣8D．4π﹣4【变式训练】1．（2023•黔江区一模）如图，一块四边形绿化园地，四角都做有半径为2的圆形喷水池，则这四个喷水池占去的绿化园地的面积为（）A．2πB．4πC．6πD．8π2．（2022•昭阳区校级模拟）如图，将半径为4，圆心角为90°的扇形BAC绕A点逆时针旋转，在旋转过程中，点B落在扇形BAC的弧AC的点B′处，点C的对应点为点C′，则阴影部分的面积为（）A．π+2B．π+4C．+πD．π﹣3．（2022•台山市校级一模）如图，正方形的边长为2，则图中阴影部分的面积为（）A．2﹣B．1﹣C．2﹣D．﹣14．（2022•金凤区校级二模）如图，在矩形ABCD中，，BC＝1，以点B为圆心，BC为半径画弧交矩形的边AB于点E，交对角线AC于点F，则图中阴影部分的面积为（）A．B．C．D．5．（2022•香洲区校级三模）如图，C为半圆内一点，O为圆心，直径AB长为2cm，∠BOC＝60°，∠BCO ＝90°，将△BOC绕圆心O逆时针旋转至△B'OC'，点C'在OA上，则边BC扫过区域（图中阴影部分）的面积为（）A．B．C．D．考点四、圆锥的计算例4（2022•十堰模拟）如图，将半径为4cm的半圆围成一个圆锥，在圆锥内接一个圆柱，当圆柱的侧面面积最大时，圆柱的底面半径是（）A．B．C．1cm D．2【变式训练】1．（2022•义乌市模拟）已知一个底面半径为3cm的圆锥，它的母线长是5cm，则这个圆锥的侧面积是（）cm2．A．15πB．45πC．30πD．20π2．（2022•五华区校级模拟）如图，在正方形ABCD中，以点A为圆心，AD为半径，画圆弧DB得到扇形DAB（阴影部分），且扇形DAB的面积为4π．若扇形DAB正好是一个圆锥的侧面展开图，则该圆锥的底面圆的半径为（）A．1B．2C．3D．43．（2022•瑶海区三模）已知直角三角形ABC的一条直角边AB＝12cm、斜边AC＝13cm，则以AB为轴旋转一周，所得到的圆锥的底面积是（）A．90πcm2B．209πcm2C．155πcm2D．25πcm24．（2022•南丹县二模）如图，圆锥体的高，底面圆半径r＝1cm，则该圆锥体的侧面展开图的圆心角的度数是（）A．60°B．90°C．120°D．150°5．（2022•高新区二模）斐波那契螺旋线也称“黄金黑旋线”，是根据斐波那契数1，1，2，3，5，……画出来的螺旋曲线．如图，在每个边长为1的小正方形组成的网格中，阴影部分是依次在以1，1，2，3，5为边长的正方形中画一个圆心角为90°的扇形，将共圆弧连接起来得到的．若用图中接下来的一个四分之一圆做圆锥的侧面，则该圆锥的底面半径为（）A．B．2C．D．411/ 1212/ 12。

第二部分 专题五 类型三1．如图所示的电路中，电源电压U 为12 V 且保持不变，电阻R 1阻值为400 Ω，电阻R 3阻值为20 Ω.当开关S 1、S 2都断开，S 3闭合时，电流表的示数为0.1 A ．求：(1)电阻R 2的阻值大小；(2)当S 1、S 2、S 3都闭合时，电路中电流表的示数是多少A? (3)当只闭合开关S 1、S 2，通电100 s 后，电路消耗多少J 的电能？解：(1) 当开关S 1、S 2都断开，S 3闭合时，R 2、R 3电阻是串联的，电流表示数0.1 A 为总电流，故R 总＝U I 总＝12 V0.1 A＝120 Ω，则R 2＝R 总－R 3＝120 Ω－20 Ω＝100 Ω；(2)当S 1、S 2、S 3都闭合时，R 3被短路了，电路中电阻R 1、R 2并联，电流表测干路中的电流大小，流过支路R 1的电流I 1＝U R 1＝12 V 400 Ω＝0.03 A ；流过支路R 2的电流I 2＝U R 2＝12 V100 Ω＝0.12 A ，故电流表示数I 总＝I 1＋I 2＝0.15 A ；(3)当电路中只有S 1、S 2闭合，而电路中干路中的开关S 3却没闭合，此时电路处于开路状态，电路中没有电流，故电路中消耗的电能为0．2．如图所示，电源电压恒定，R 2＝6 Ω，R 3＝12 Ω，滑动变阻器R 1的滑片P 滑到中点，当开关S 1、S 2、S 3都闭合时，电流表A 的示数为3 A ；当开关S 1闭合S 2、S 3都断开时，电流表A 的示数为0.6 A ．求：(1)电源电压；(2)滑动变阻器R 1的最大阻值；(3)当S 1、S 3闭合、S 2断开时，电路消耗的总功率． 解：(1)当开关S 1、S 2、S 3都闭合时，R 2、R 3并联 由1R 并＝1R 2＝1R 3得：R 并＝6 Ω×12 Ω6 Ω＋12 Ω＝4 Ω U ＝I 并R 并＝3 A ×4 Ω＝12 V(2)当开关S 1闭合，S 2、S 2都断开时，R 1、R 2串联因此R 串＝U I 串＝12 V 0.6 A＝20 Ω，所以R 1＝(R 串－R 2)×2＝(20 Ω－6 Ω)×2＝28 Ω(3)当S 1、S 3闭合，S 2断开时，只有R 2工作，所以P 总＝U 2R 2＝(12 V )26 Ω＝24 W ．3．阳阳发现家里的饮水机全天一直在工作，于是从市场上购买了某品牌智能定时插座，如图所示，该插座可以设置不同的时间段内自动通、断电，从而达到节能的目的，下表是该插座的参数表，请回答以下问题.品牌名称 ××牌插座 产品型号 AL －06 额定电压 220 V 时控范围 1 min －168 h额定电流 10 A 待机功率 <1 W 产品净重 145 g产品材质无毒环保适用范围饮水机、热水器、各类充电器、路灯、广告牌、喷泉控制等(1)该智能插座允许接入用电器的最大电功率为多少．(2)若饮水机的保温功率为40 W ，将开启时间段设置为7：00－7：30和18：00－21：30 (该时段内在家且可能需要饮水)，在其他条件相同的条件下，每天大约可以节约多少电能？(插座消耗的电能忽略不计)(3)若在某段时间内总共节能1 kW·h ，用这些电能最多可以将多少kg 初温为20 ℃的水加热至70 ℃？[水的比热容为4.2×103 J/(kg·℃)，最后结果保留一位小数]解：(1)最大电功率P ＝UI ＝220 V ×10 A ＝2 200 W (2)每天减少使用时间t ＝20 h节约的电能W ＝P 保温t ＝0.04 kW ×20 h ＝0.8 kW·h ＝2.88×106 J (3)由W ＝Q 吸＝cm Δtm ＝Q 吸c Δt ＝ 3.6×106 J4.2×103 J/(kg·℃)×(70 ℃－20 ℃)≈17.1 kg ．4．(2016岳阳)图甲为某款新型电饭煲，额定电压为220 V ，它采用了“聪明火”技术，智能化地控制不同时间段的烹饪温度，以得到食物最佳的营养和口感，图乙为其电路原理图，R 1和R 2为电阻不变的电热丝，S 1是自动控制开关．将电饭煲接入220 V 电路中，在电饭煲工作的30 min 内，它消耗的电功率随时间变化的图象如图丙所示．求：(1)0～30 min ，电饭煲产生的总热量； (2)S 和S 1均闭合，电路中的总电流；(3)在不同电压下，电饭煲从开始工作到S 1第一次自动断开产生的热量相同．用电高峰期，当实际电压为198 V 时，使用该电饭煲，从开始工作到S 1第一次自动断开需要多长时间．甲 乙 丙解：(1)由电路图可知，当开关S 和S 1都闭合时，电路为R 1与R 2并联，电饭煲的功率较大；同理可知，只闭合开关S 、断开S 1时，电路为R 1的简单电路，电饭煲功率较小； 由图乙可知，工作30 min 中，P 1＝440 W 时的时间t 1＝15 min ＝900 s ，P 总＝660 W 时的时间t 2＝30 min －15 min ＝15 min ＝900 s ，由Q ＝W ＝UIt 可得，0～30 min 内电饭煲产生的总热量：Q ＝Q 1＋Q 2＝W 1＋W 2＝P 1t 1＋P 总t 2＝440 W ×900 s ＋660 W ×900 s ＝9.9×105 J ； (2)当S 和S 1均闭合时，电阻R 1与R 2并联，电饭煲的功率较大， 由P ＝UI 可得，电路中的总电流： I 总＝P 总U ＝660 W 220 V＝3 A ；(3)电饭煲正常工作时，由图丙可知，电饭煲从开始工作到S 1第一次自动断开时的时间t ＝10 min ＝600 s ，此过程中产生的热量：Q ′＝W ＝P 总t ＝660 W ×600 s ＝3.96×105 J ， 电饭煲最大功率时电路中的总电阻： R ＝U 2P 总＝(220 V )2660 W＝2203 Ω，因在不同电压下，电饭煲从开始工作到S 1第一次自动断开产生的热量相同， 所以，由Q ＝W ＝U 2R t 可得，在实际电压是198 V 时，电饭煲工作的时间：t ′＝Q ′RU 2实＝3.96×105 J ×2203 Ω(198 V )2≈740.7 s ．5．如图1为一款利用高温水蒸气熨烫衣服的便携式挂烫机，它的正常工作电压为220 V ，水箱装水最多0.3 kg ，加热功率有大小两个挡位，设计师最初设计的内部电路有如图2的甲、乙两种接法，其中电热丝R 1＝56 Ω，R 2＝44 Ω．(1)如果选择甲电路，电路中最大电流为__5__A ，如果选择乙电路，电路中最大电流为__8.9__A ，由于两个电路中所选熔断器里的熔丝允许通过的最大电流为8.2 A ，故设计师最终选择了甲电路；(计算结果保留一位小数)(2)请分别计算这款挂烫机两个挡位的额定功率；(3)若将水箱中0.22 kg 的水从25 ℃加热到100 ℃，挂烫机至少需要加热多长时间？[水的比热容c ＝4.2×103 J/(kg·℃)]解：(1)如果选择甲电路，当开关旋至1、2之间时，电路中只有电阻R 2工作，此时的电路中的最大电流I 大＝U R 2＝220 V44 Ω＝5 A ；如果选择乙电路，当开关旋至1、2之间时，R 1、R 2并联，电路中的最大电流，I 大′＝I 1＋I 2＝U R 1＋U R 2＝220 V 56 Ω＋220 V44 Ω≈3.9 A ＋5 A ＝8.9 A ；(2)甲电路，P 1＝UI 大＝220 V ×5 A ＝1 100 W ； P 2＝U 2R 1＋R 2＝(220 V )256 Ω＋44 Ω＝484 W ；乙电路：P 1′＝UI ′大＝220 V ×8.9 A ＝1 958 W ； P 2′＝U 2R 1＝(220 V )256 Ω≈864 W ；(3)水吸收的热量：Q ＝cm (t －t 0)＝4.2×103J/(kg·℃)×0.22 kg ×(100 ℃－25 ℃)＝6.93×104 J ，由P ＝W t 得，所需时间t ＝W P 1＝6.93×104J 1 100 W＝63 s ．。

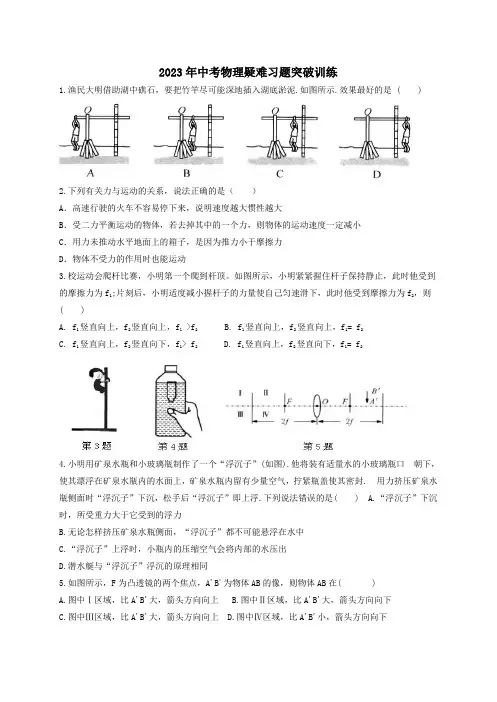
2023年中考物理疑难习题突破训练1.渔民大明借助湖中礁石，要把竹竿尽可能深地插入湖底淤泥.如图所示.效果最好的是 ( )2.下列有关力与运动的关系，说法正确的是（）A．高速行驶的火车不容易停下来，说明速度越大惯性越大B．受二力平衡运动的物体，若去掉其中的一个力，则物体的运动速度一定减小C．用力未推动水平地面上的箱子，是因为推力小于摩擦力D．物体不受力的作用时也能运动3.校运动会爬杆比赛，小明第一个爬到杆顶。

如图所示，小明紧紧握住杆子保持静止，此时他受到的摩擦力为f1;片刻后，小明适度减小握杆子的力量使自己匀速滑下，此时他受到摩擦力为f2，则( )A. f1竖直向上，f2竖直向上，f1 >f2B. f1竖直向上，f2竖直向上，f1= f2C. f1竖直向上，f2竖直向下，f1> f2D. f1竖直向上，f2竖直向下，f1= f24.小明用矿泉水瓶和小玻璃瓶制作了一个“浮沉子”(如图).他将装有适量水的小玻璃瓶口朝下，使其漂浮在矿泉水瓶内的水面上，矿泉水瓶内留有少量空气，拧紧瓶盖使其密封. 用力挤压矿泉水瓶侧面时“浮沉子”下沉，松手后“浮沉子”即上浮.下列说法错误的是( ) A.“浮沉子”下沉时，所受重力大于它受到的浮力B.无论怎样挤压矿泉水瓶侧面，“浮沉子”都不可能悬浮在水中C.“浮沉子”上浮时，小瓶内的压缩空气会将内部的水压出D.潜水艇与“浮沉子”浮沉的原理相同5.如图所示，F为凸透镜的两个焦点，A'B'为物体AB的像，则物体AB在( )A.图中Ⅰ区域，比A'B'大，箭头方向向上B.图中Ⅱ区域，比A'B'大，箭头方向向下C.图中Ⅲ区域，比A'B'大，箭头方向向上D.图中Ⅳ区域，比A'B'小，箭头方向向下6.如图所示、小华斜向上拉着行李箱匀速行走在水平路面上。

下列说法正确的是（）A.小华先对行李箱有力的作用，行李箱后对小华有力的作用B.小华对行李箱的拉力与地面对行李箱的摩擦力是一对平衡力C.小华拉着行李箱运动的过程中，行李箱的机械能保持不变D.地面对行李箱的支持力和行李箱的重力是一对平衡力7.如图所示，在一个较大容器的水面上放一木块，本块上面放一个体积为1dm3，重12N的物体，此时木块漂浮。