为什么距离增加1倍声压级减少6dB
- 格式:doc
- 大小:21.50 KB
- 文档页数:2

点声源随距离衰减规律
声波是一种机械波,需要介质来传播。
声波传播时会遇到介质的阻力
和摩擦力,这些阻力和摩擦力会使声波的能量逐渐减弱,导致声音随
距离衰减。
声音的衰减规律主要受到以下因素的影响:
1. 距离:声音的衰减程度与距离成正比。
当距离增加时,声音的能量
逐渐分散,导致声音强度下降。
2. 声源功率:声源功率越大,能够产生的声压级也越高。
因此,在相
同距离下,功率较大的声源产生的声压级也更高。
3. 声波频率:不同频率的声波在传播过程中受到不同程度的衰减。
低
频声波相对于高频声波更容易穿透障碍物和远距离传播。
4. 环境:不同环境中对于声音有着不同程度的吸收和反射作用。
例如,在空气中传播时,由于空气分子之间存在着摩擦作用,因此空气对于
高频声波的吸收作用更强。
综合以上因素,声音的衰减规律可以用以下公式表示:
L = L0 - 20log(d) - 11 + 10log(P)
其中,L为声音的声压级,L0为参考声压级,d为距离,P为声源功率。
这个公式表明了在相同环境下,距离每增加一倍,声压级就会降
低6dB。
而当距离相同时,功率每增加10倍,声压级就会增加10dB。
需要注意的是,在实际应用中,不同环境下的衰减规律可能会有所不同。
例如,在室内和室外传播时,由于环境不同所以衰减规律也不同。
因此,在进行实际应用时需要根据具体情况进行调整。
总之,在了解了点声源随距离衰减规律后,我们可以更好地控制和设
计声学系统,并在实际应用中做出更加准确和合理的判断和决策。

关于扬声器声压级换算的讨论很多电声工程师知道扬声器功率增加一倍,声压级提高3dB,反之降低;测试距离增加一倍,声压级降低6dB,反之提高。
但如果遇到以下问题,有多少人能够回答?某扬声器在1m/W 的情况下声压级为85dB,问在3m/5W 的情况下声压级为多少?本人现凭借大学时学到的一点肤浅的声学知识,将计算方法推导一下 1.声压级定义公式为refp p SPL e lg 20=,其中为Pa,这个数值是正常人耳对1kHz 声音刚刚能觉察其存在的声压值,也就是1kHz 声音的可听阈声压。
换句话说,人耳刚刚可以觉察到的1kHz 声音的声压级是0dB。
ref p 5102−×声强级定义公式ref I I10lg SIL =,其中为声强,正比于扬声器的输入电功率。
在常温条件下,可以认为。
具体分析如下:I SIL SPL =现定义某声场中,单位体积内的平均声能量为ε(3m J ),即为平均声能量密度,很明显声能量密度ε正比于扬声器的输出声功率,进而正比于输入电功率。
再定义0c Iε=(为声速),即为单位时间内通过垂直于声传播方向上单位面积的平均声能量流,叫做声强。
0c 通过声波方程解析可以证明002c p I e ρ=(0ρ为空气密度);而是参考声压为,refI ref p 00c ρ为400的情况下得出的数值,即为。
所以m s N /⋅212/10m W −002002400lg 10400lg 10lg 10c SPL p c p I ISIL ref e ref ρρ+=⎟⎟⎠⎞⎜⎜⎝⎛⋅== 如果在测量时,条件恰好为40000=c ρ,则SIL SPL =;对一般情况,两者相差一个修正项00400lg 10c ρ,而通常这个修正项很小。
所以,要计算相同距离不同功率下的声压级可以通过计算声强级的方法获得。
如下式12121212lg 10lg 10lg 10I I I I I I SIL SIL SPL SPL ref ref =−=−=− 由于,所以功率增加一倍,声压级增加3dB3.02lg =2.通过对于点声源的分析,可以得出结论:声压与距离r 成反比。
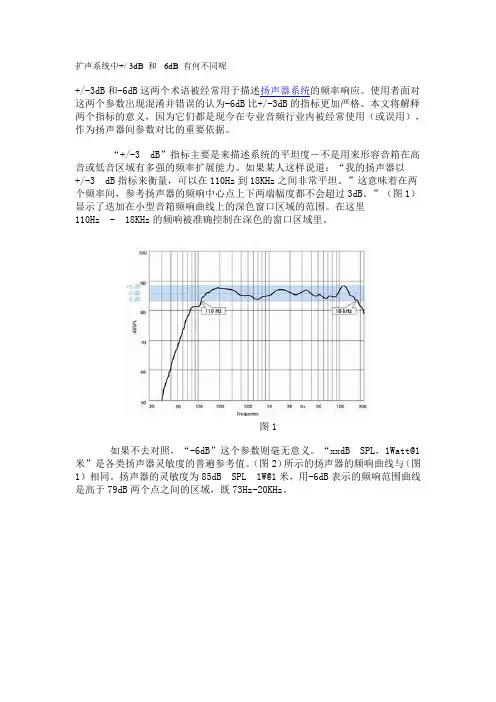
扩声系统中+/-3dB 和-6dB 有何不同呢+/-3dB和-6dB这两个术语被经常用于描述扬声器系统的频率响应。
使用者面对这两个参数出现混淆并错误的认为-6dB比+/-3dB的指标更加严格。
本文将解释两个指标的意义,因为它们都是现今在专业音频行业内被经常使用(或误用),作为扬声器间参数对比的重要依据。
“+/-3 dB”指标主要是来描述系统的平坦度-不是用来形容音箱在高音或低音区域有多强的频率扩展能力。
如果某人这样说道:“我的扬声器以+/-3 dB 指标来衡量,可以在110Hz到18KHz之间非常平坦。
”这意味着在两个频率间,参考扬声器的频响中心点上下两端幅度都不会超过3dB。
”(图1)显示了迭加在小型音箱频响曲线上的深色窗口区域的范围。
在这里110Hz - 18KHz的频响被准确控制在深色的窗口区域里。
图1如果不去对照,“-6dB”这个参数则毫无意义。
“xxdB SPL,1Watt@1米”是各类扬声器灵敏度的普遍参考值。
(图2)所示的扬声器的频响曲线与(图1)相同。
扬声器的灵敏度为85dB SPL 1W@1米,用-6dB表示的频响范围曲线是高于79dB两个点之间的区域,既73Hz-20KHz。
图2如果说+/-3dB所表示的是平坦特性,而不是频率响应范围,那么这个参数对频率特性而言还有什么意义?回答这个问题前我们可以看一下制造商在典型扬声器说明书上所标注的“+/-3dB频响。
”扬声器书面参数为:灵敏度 (1瓦@1米) 99dB SPL频率响应 (+/-3dB) 50Hz-20KHz制造商是想表达频响的平坦性吗?(图3)显示了在频响曲线上的一个深色的+/-3dB“平坦”区域,尽管这个窗口区域想涵盖所有的频响范围,不过最终由于59Hz和2.8KHz超出了-3dB的范围,毫无疑问,该扬声器在+/-3dB 参考标准下不能满足50Hz-20KHz频响要求。
图3该扬声器制造商或许是从99dB SPL灵敏度为参考基准来衡量这个+/-3dB。

声强随距离变化原理“声强随距离变化原理”,简而言之,就是声音强度随着距离的增加而减弱。
这个原理在我们日常生活中非常常见,比如在室外听到远处的车声、人声,声音明显比在室内听到的弱很多。
那么,这个原理是如何产生的呢?下面就来介绍一下声强随距离变化的基本原理:步骤一:声音传播的基本概念首先,我们需要了解声音的传播方式。
声音是通过介质传播的,比如空气、水等。
当声源发出声音时,会在介质中形成声波,声波会以一定的速度传播,直到遇到障碍物或者扩散到环境中所有的角落。
步骤二:声音强度的定义在介绍声音强度与距离的关系之前,我们需要先了解声音强度的基本定义。
声音强度是指单位面积上单位时间内通过的能量,即每秒钟传播到单位面积上的声功率。
单位是瓦特每平方米(W/m²)。
步骤三:声音强度与距离的关系接下来,我们就可以讲述声音强度与距离的关系了。
当声波从声源传播到一定距离后,因为周围介质的吸收和散射作用,声波能量会逐渐减弱,导致声音强度随着距离的增加而减弱。
声音强度随距离的关系是一个与距离平方成反比例关系的指数函数,即:I1/I2 = (r2/r1)²其中,I1和I2分别表示两个不同距离上的声音强度,r1和r2分别表示两个不同距离。
可以看到,当距离成倍增加时,声音强度会下降四倍。
步骤四:对声音传播的影响因素除了距离因素之外,还有很多其他因素会影响声音传播的效果,比如介质的密度、温度、湿度等。
不同介质的声速不同,会影响声波在介质中传播的速度和穿透性。
而温度和湿度等因素则会影响声波的传输路径,影响声音的可听性。
综上所述,声强随距离变化原理是由声波的传播过程导致的。
随着距离的增加,声波在介质中的能量逐渐减弱,导致声音强度随着距离的增加而减弱。
在实际生活中,我们需要注意控制环境噪声,提高声音传播的质量和可听性。


也谈“两个音箱叠加,声压级上升6db还是3db?”今天偶尔看到这个过去大家讨论很热烈的帖子:“请教!在理想状态下,两个音箱叠加,声压级上升6db还是3db?”看完大家的讨论过程,我认为有必要做些梳理和明确:首先,我同意曾山的6db的结论,但是前提是两只音箱叠加,而且,他关于两只音箱效率的说法我认为不妥。
下面我来说说为什么。
我们都知道:声压级的增加值可以通过下面的公式计算得出:@SPL=10lg P1-10lg Po =10lg P1/Po就一只音箱而言,功率增加一倍,即:P1=2 x Po,此时,声压级增加:@SPL=10lg P1/Po =10lg 2Po/Po =3dB;当两只音箱叠加时,功率自然是增加了一倍,但是别忘了:“负载也变了!!!”音箱的叠加可以等效为电路的并联:想象一下,假设两只音箱完全重合(这虽然不可能),相当于输入功率增大一倍,同时音圈的截面积增大一倍而圈数未变,此时并联等效阻抗为原阻抗的1/2,即:R=1/2Ro ,此时,并联电路里电压是恒定因子。
那可推导出,此时的声压级为:SPL= 10lg P1=10lg 2 Po’=10lg 2 U2 /R=10lg 2 U2 /Ro/2=10lg 4 U2 /Ro=10lg 4 Po因此,声压级的增加值为: @SPL=10lg P1-10lg Po=10lg P1/Po=10lg 4Po /Po=6dB.其实,关于这个问题早在2001年时,就和曾山有过讨论,后来,我也做过多次的测试和实践,该结论我在中国影视声音学会的论文集里也做过论述。
功率每增加一倍,可以按照声压级增大3dB去推算。
但是,音箱每增加一只,就不能按照这个理论去计算了。
因为此时两个条件变了:第一,功率增大了;第二,发声体体量增大了,相当于负载阻抗减小了。
由此,我们能够推算出:1只音箱: @SPL: +0dB2只音箱: @SPL: +6dB3只音箱: @SPL: +9.5dB4只音箱: @SPL: +12dB5只音箱: @SPL: +14dB. . . . . .8只音箱: @SPL: +18dB. . . . . .16只音箱: @SPL: +24dB仅供大家参考和讨论!。

声学系统名词解释一、声学1、最大声压级:扩声系统在厅堂听众席处产生的最高稳态准峰值声压级。
另一解释:在扩声系统中,音箱所能发出的最大稳态声压级,最大声压级越高,说明系统的功率储备就大,声音听起来底气足、动态大、坚实有力。
决定扩声系统最大声压的因素主要是功放、音箱总功率和声场大小等。
音箱等设备所能达到的最大稳态声压,人耳不能承受120BD的音量,舒服的情况下是85DB,从70DB到73DB声音+3DB声音放大一倍。
2、最高可用增益:扩声系统在所属厅堂内产生反馈自激临界增益减去6dB时的增益。
另一解释:扩声系统在反馈自激(啸叫)临界状态的增益减去6分贝时的增益,此时扩声系统应绝对没有声反馈现象存在。
在反馈临界状态下,由于还存在振铃现象,即声音停止发声后音箱中会继续有尾音(余音),还会对音质造成破坏,声反馈的影响并没有消除,减去6分贝后这种现象消失,定为最高可用增益。
此值越高,说明话筒路声音的放大能力越强,声反馈啸叫抑制得好,话筒路声音可以开得很大。
当啸叫发生时,下降6DB就达到了设备的最大稳态可用增益。
3、传输频率特性:扩声系统达到最高可用增益时,厅堂内各听众席处稳态声压的平均值相对于扩声系统传声器处声压或扩声设备输入端的电压的幅频响应。
另一解释:扩声系统的频率响应特性,为房间和音响设备共同的频响特性,考察系统是否能够将各频率声音音量比例真实再现,即对各个频率的信号放大量一致,优秀的扩声系统,不应该出现某些频率声音过强、某些频率声音不足的现象。
获得良好的传输频率特性的主要方法有:合理的建声设计、用粉红噪声频谱分析仪法调整均衡器以及采用频率响应特性好的音箱放音等。
在声音处理时频率要平稳,这样表示设备的性能较好,或者说音箱能够较好的还原声音4、传声增益:扩声系统达最高可用增益时,厅堂内和听众席处稳态声压级的平均值与扩声系统传声器处声压级的差值。
另一解释:扩声系统在使用话筒时,对话筒拾取的声音的放大量,是考察扩声系统声反馈啸叫程度的重要指标,传声增益越高,声反馈啸叫越小(少),话筒声音的放大量越大。

声学系统名词解释一、声学1、最大声压级:扩声系统在厅堂听众席处产生的最高稳态准峰值声压级。
另一解释:在扩声系统中,音箱所能发出的最大稳态声压级,最大声压级越高,说明系统的功率储备就大,声音听起来底气足、动态大、坚实有力。
决定扩声系统最大声压的因素主要是功放、音箱总功率和声场大小等。
音箱等设备所能达到的最大稳态声压,人耳不能承受120BD的音量,舒服的情况下是85DB,从70DB到73DB声音+3DB声音放大一倍。
2、最高可用增益:扩声系统在所属厅堂内产生反馈自激临界增益减去6dB时的增益。
另一解释:扩声系统在反馈自激(啸叫)临界状态的增益减去6分贝时的增益,此时扩声系统应绝对没有声反馈现象存在。
在反馈临界状态下,由于还存在振铃现象,即声音停止发声后音箱中会继续有尾音(余音),还会对音质造成破坏,声反馈的影响并没有消除,减去6分贝后这种现象消失,定为最高可用增益。
此值越高,说明话筒路声音的放大能力越强,声反馈啸叫抑制得好,话筒路声音可以开得很大。
当啸叫发生时,下降6DB就达到了设备的最大稳态可用增益。
3、传输频率特性:扩声系统达到最高可用增益时,厅堂内各听众席处稳态声压的平均值相对于扩声系统传声器处声压或扩声设备输入端的电压的幅频响应。
另一解释:扩声系统的频率响应特性,为房间和音响设备共同的频响特性,考察系统是否能够将各频率声音音量比例真实再现,即对各个频率的信号放大量一致,优秀的扩声系统,不应该出现某些频率声音过强、某些频率声音不足的现象。
获得良好的传输频率特性的主要方法有:合理的建声设计、用粉红噪声频谱分析仪法调整均衡器以及采用频率响应特性好的音箱放音等。
在声音处理时频率要平稳,这样表示设备的性能较好,或者说音箱能够较好的还原声音4、传声增益:扩声系统达最高可用增益时,厅堂内和听众席处稳态声压级的平均值与扩声系统传声器处声压级的差值。
另一解释:扩声系统在使用话筒时,对话筒拾取的声音的放大量,是考察扩声系统声反馈啸叫程度的重要指标,传声增益越高,声反馈啸叫越小(少),话筒声音的放大量越大。

6db法则在音频处理领域,6dB法则是一条常见的规则,用于指导声音的增益调整和音量平衡。
这个法则得名于每增加6dB,声音的强度会加倍。
在音频工程中,我们经常需要调整音频信号的强度,以确保音量适宜,同时保持音频的清晰度和动态范围。
我们来了解一下什么是分贝(dB)。
分贝是一种用于测量声音强度的单位,它是对数比例单位。
分贝的计算公式是:dB = 10 × log10(P1/P0),其中P1是当前声音的强度,P0是参考声音的强度。
在音频处理中,通常使用0 dB作为参考点,表示原始录音或信号的强度。
根据6dB法则,每增加6dB,声音的强度就会加倍。
这意味着如果我们将音频信号的增益提高6dB,它的声音强度将翻倍。
同样,如果我们将音频信号的增益降低6dB,它的声音强度将减少一半。
这是因为分贝是基于对数比例的单位,对数函数的性质使得每增加6dB就相当于乘以2,每减少6dB就相当于除以2。
6dB法则在音频处理中有着广泛的应用。
首先,它可以用于平衡不同音频信号的音量。
当我们将多个音频信号混合在一起时,可能会出现某些信号过于强大,而另一些信号过于微弱的情况。
通过使用6dB法则,我们可以调整各个音频信号的增益,使它们在混音后的结果中保持相对平衡。
6dB法则可以用于控制音频信号的动态范围。
动态范围是指音频信号中最强和最弱部分之间的差异。
如果动态范围过大,可能会导致某些部分过于响亮,而其他部分则听不清。
通过使用6dB法则,我们可以调整音频信号的增益,使动态范围适中,以确保音频的清晰度和可听性。
6dB法则还可以用于避免声音失真。
当音频信号过于强大时,可能会超过音频设备的处理范围,导致失真和破裂的声音。
通过使用6dB法则,我们可以适当地降低音频信号的增益,以避免失真问题的发生。
需要注意的是,6dB法则并不是一个绝对的规则,它只是一种指导原则。
在实际应用中,我们还需要考虑其他因素,如音频设备的特性和所需的音频效果。
此外,不同的音频处理软件和设备可能具有不同的增益控制方式和单位,因此在具体操作时需要根据实际情况进行调整。

关于MIC的灵敏度2010-06-15 21:32阅读(765)评论(0)MIC的灵敏度标示参数有-30db,-40db什么的,以前一直以为它的数越小灵敏度越大,即负的越多采集的电压越高。
近来重新查阅资料,才发现此为谬。
灵敏度是按以下公式计算的:S=20Lg(V/V0),其中V0=1V , V为1Pa声压下传声器的输出电压例如 V=0.01V(即在1PA声压下输出0.01V),则灵敏度S=20Lg0.01=-40dBPa为压强的国际单位,而我们常用分贝表示声音大小,人正常说话的声音是50dB SPL ~115dB SPL。
SPL是声压级的简称。
分贝与帕的换算:dB SPL = 20 x Lg (pa / 0.00002)举例如下:40dBSPL=0.002Pa50dBSPL=0.0032Pa60dBSPL=0.02Pa80dBSPL=0.2Pa94dB SPL=1Pa115dB SPL=11.22Pa。
若设MIC的灵敏度为-43dB,则算出7.08mVrms/Pa。
在11.22Pa,也就是115dB时,输出电压7.08*11.22=79.4mVrms(峰峰值是224mV,rms有效值)同理,其它值是:0.0032Pa:MIC的输出电压是0.0224mVrms。
0.2Pa: MIC的输出电压是15.88Vrms0.02Pa: MIC的输出电压是1.588mVrms再说声音传播的衰减,它与距离的平方成反比。
与音源之间的距离每增加一倍,声压就会下降12dbspl(声压为1/4,20*Lg(a)-20*Lg(a/4)=20*Lg4).这里的声压与声强(单位面积的功率单位)不同,声强单位是DBSIL, SIL=10*Lg(I/I0)与音源之间的距离每增加一倍,声强就会下降6db网上有些资料比较乱,常把声压与声强的DB搞混,比如说距离每增加一倍,声压就会下降6dbspl,我觉得是不对的,这里应是声强才对。
但不管怎么说,对于MIC来讲,相同声音,距离每增加一倍,输出电压会变为1/4。
音源与听者之间的声压级与距离的关系引言:音乐是我们生活中难以分割的一部分,而对于音乐的正确聆听也有其科学性。
在音源与听者之间,声压级与距离是一个十分重要的关系。
通过了解这一关系,我们可以更好地把握音乐的美妙。
声压级与距离的基本原理声压级是指声音的强弱程度,单位为分贝(dB)。
而距离则是指音源与听者之间的物理距离。
声压级与距离之间的关系可用倒数平方定律来描述。
根据这一定律,当听者距离音源加倍时,声压级会减弱约6分贝。
这是因为声波在传播过程中会遇到空气阻力和扩散现象,导致声音的能量逐渐减弱。
声压级对听觉的影响声压级的高低直接影响着我们的听觉感受。
当声压级较低时,音乐听起来比较柔和、平静,适合用来放松或者休息。
而当声压级较高时,音乐则会更具冲击力和激动感,适合用来驱散疲劳或者增加气氛。
因此,在不同场合下,选择合适的声压级对于营造氛围和提升音乐体验至关重要。
声压级的影响因素除了距离的变化外,还有许多因素会对声压级产生影响。
首先,音源的功率是决定声压级高低的关键因素之一。
功率越大,声压级也会相应增加。
其次,环境的噪声水平也会影响声压级的感知。
如果环境中噪声较大,我们需要增加音乐的声压级才能够更好地听到音乐本身。
最后,听者的个体差异也会对声压级产生影响。
一些人对声音较为敏感,对于相同的声音会感到更强烈,而另一些人则相对不敏感。
这一点需要在选择合适的声压级上加以考虑。
最佳听音距离在享受音乐时,选择合适的听音距离也是至关重要的。
一般来说,最佳听音距离是离音源的距离约为2-3倍音源间距离的位置,这样可以在保持音乐的细腻性同时,不会过度强化或弱化音乐的某些频率。
此外,在房间环境中,合理调整音箱与听者之间的距离也有助于提升音乐的还原度和立体感。
结语:在音源与听者之间的声压级与距离的关系中,了解声压级的变化规律以及适宜的听音距离对于保持音乐的优良品质和提升音乐体验具有重要意义。
通过科学的方法和合理的调整,我们可以更好地享受到音乐带来的美妙与愉悦。
完整版)建筑物理题库1.根据《民用建筑热工设计规范》,夏热冬冷地区的热工设计必须同时满足冬季保温和夏季防热。
2.正确的叙述应该是:规定正午(当地真太阳时)时,时角的值为0,时角随时间而变化,每隔一小时增加15°。
3.窗口遮阳的挑出长度与太阳的位置、墙的方位角、窗户的高度有关,但与窗户的宽度无关。
4.封闭空气间层内贴上铝箔后,空气间层的热阻大量增加是因为铝箔增加了空气间层的导热热阻。
5.当围护结构的总衰减度为6.5,室外温度谐波振幅为16.25℃时,围护结构内表面受该室外温度谐波的作用而产生的温度波动的振幅为4.5℃。
6.正确的叙述是:空气中水蒸气的饱和蒸汽压随空气温度的增加而增加。
7.进行外围护结构的隔热设计时,应该选择太阳辐射的当量温度作为室外热作用。
8.增加砖墙的厚度、增设一保温材料层、设置封闭空气间层和砖墙外表面做浅色饰面都是合理的措施,没有不合理的选项。
9.在稳定传热中,通过多层平壁各材料层的热流强度应该是通过各材料层的热流强度不变。
10.错误的叙述是:同一时刻,建筑物各表面的太阳辐射照度相同,实际上建筑物不同表面的太阳辐射照度会因为方向、遮挡等因素而不同。
11.正确的排列应该是:水泥砂浆、钢筋混凝土、重砂浆、黏土砖砌体。
1.白炽灯、普通管形荧光灯、金属卤化物灯和无紫外线管形荧光灯都是不同种类的照明设备。
2.在采光计算中,单侧窗采光的计算点通常位于距离窗口1米的位置。
3.建筑采光设计中,采光等级分为2、3、4和5级。
4.在明亮的环境中,人眼对黄绿色光最敏感。
5.顶部采光时,Ⅰ—Ⅳ级采光等级的采光均匀度要求不小于0.9.6.在点声源的情况下,接受点与声源的距离增加一倍,声压级大约降低6dB。
7.吸声量的单位是无量纲。
8.在用伊林公式计算混响时间时,需要考虑1000Hz及其以上频率的声音对空气吸收的影响。
9.4个相同的声压级声音迭加,总声级比单个增加6dB。
10.避免厅堂简并现象最有效的措施是强吸声。
声压就是大气压受到扰动后产生的变化,即为大气压强的余压,它相当于在大气压强上的叠加一个扰动引起的压强变化。
由于声压的测量比较容易实现,通过声压的测量也可以间接求得质点速度等其它物理量,所以声学中常用这个物理量来描述声波。
声压的单位是帕斯卡(pa),其计算公式为:声压(p)的平方=声强(I)×介质密度(ρ)×声速(C)其中,声强单位是:W/m2 密度单位:kg/m3 声速:m/s声波通过媒质时,由于振动所产生的压强改变量。
它是随时间变化的,实测声压是它的有效值。
单位是Pa或MPa。
表示声压大小的指标称为声压级(sound pressure level),用某声音的声压(p)与基本声压值(p0)之比的常用对数的20倍来表示,即20lgP/P0,单位为dB。
声音是由物体振动产生,正在发声的物体叫声源。
声音以声波的形式传播。
声音只是声波通过固体或液体、气体传播形成的运动。
声波振动内耳的听小骨,这些振动被转化为微小的电子脑波,它就是我们觉察到的声音。
内耳采用的原理与麦克风捕获声波或扬声器的发音一样,它是移动的机械部分与气压波之间的关系。
自然,在声波音调低、移动缓慢并足够大时,我们实际上可以“感觉”到气压波振动身体。
因此我们用混合的身体部分觉察到声音。
实际应用:DSP458(120W防水音柱),最大声压级是115dB, 距离每增加1倍,声压级就减少6个dB 1米有115dB,2米有109dB,4米有103dB,8米有97dB,16米有91dB,32米有85dB,64米有79个dB去到64米就只剩下64个dB了,和你环境噪音一比,因为通常要比环境噪音高10-15个dB,人才能听得清讲话的声音。
某工厂冷却塔附近(1m处)声压级为105db而厂界标准要求值为60DB,试问冷却塔距离厂界应为多少米把声级的计算公式找出来,跟距离的关系代入就可以算出来了。
首先确定,这是点源,用点声源衰减公式:点声源的声音向外发散遵循球面分布规律,在距离点声源r1、r2处的衰减值:L=20lg(r1/r2)=20lgX (20lg=1.301029995663981)距离冷却塔x米处噪声60=105-L声压级计算公式Lp=20lg(p/p0)式中,Lp:声压级(单位:分贝);p:声压(单位:帕);p0:基准声压,在空气中p0=2×10的-5次方(帕),即20微帕。
声强或声压与距离的关系在物理学中,声音的音量和距离之间的关系是由声波的传播特性决定的。
声音的音量,通常用声压或声强来表示,随着传播距离的增加,会经历一个由大到小,再到由小到大的变化过程。
这是因为声音在传播过程中会受到空气阻尼、散射和吸收等效应的影响。
一、声压与距离的关系声压是声音在空气中传播时产生的压力变化。
在自由声场中,声音的声压随传播距离的增加而减小。
这是因为声波在传播过程中,能量会逐渐散失。
这种散失主要是由于空气分子的热运动引起的,即空气分子的随机振动对声波的能量有一定的耗散作用。
根据物理学中的平方反比定律,声压与距离的平方成反比。
也就是说,如果声音传播的距离增加一倍,声压将减小到原来的四分之一。
这个关系适用于声音在理想的无损媒质中传播的情况。
然而,在实际环境中,由于空气的阻尼、散射和吸收等效应,声压随距离的变化关系可能会略有不同。
二、声强与距离的关系声强是单位时间内通过单位面积的声能,它是表示声音强弱的重要物理量。
在自由声场中,由于声波的传播不受外界的明显阻碍,因此声强随传播距离的增加而减小。
这个减小也是遵循平方反比定律的,即声强与距离的平方成反比。
然而,需要注意的是,当声音遇到障碍物或者其他声学介质时,声强会在障碍物或介质表面发生反射、折射或者散射。
在这种情况下,声强与距离之间的关系将变得更为复杂,取决于具体的反射、折射和散射规律。
三、实际应用在实际应用中,了解声音音量和距离之间的关系对于许多领域都非常重要。
例如:在城市规划中,需要考虑不同建筑物对声音传播的影响;在噪声控制中,需要了解如何有效地降低噪声对周围环境的影响;在音频工程中,需要精确地调整扬声器系统的位置和方向,以确保声音覆盖到预期的区域而不会干扰到其他区域。
综上所述,声音的音量和距离之间的关系主要受到空气阻尼、散射和吸收等效应的影响。
在自由声场中,声压和声强都遵循平方反比定律,随传播距离的增加而减小。
然而,在实际应用中,需要考虑各种声学介质和障碍物对声音传播的影响。
汽车声压与距离的计算公式在日常生活中,我们经常会遇到汽车的噪音。
汽车的引擎、轮胎与路面的摩擦、车辆间的摩擦等都会产生噪音。
而这些噪音会随着距离的增加而减弱。
那么,汽车声压与距离之间究竟有怎样的关系呢?下面我们将通过计算公式来探讨这个问题。
首先,我们需要了解声压的定义。
声压是指声波对单位面积的作用力。
在国际单位制中,声压的单位为帕斯卡(Pa)。
声压与声音的强度有关,而声音的强度又与声波的振幅有关。
因此,声压与声波的振幅成正比。
当声波传播时,其振幅会随着距离的增加而减小,从而导致声压的减小。
接下来,我们来探讨声压与距离之间的计算公式。
根据声学原理,声波在传播过程中会遵循反比关系。
也就是说,声压与距离的平方成反比。
这个关系可以用下面的公式来表示:P = P0 (d0 / d)^2。
其中,P表示距离为d处的声压,P0表示距离为d0处的声压,d0表示参考距离,d表示要计算声压的距离。
在这个公式中,我们可以看到声压与距离的平方成反比。
也就是说,当距离增加一倍时,声压会减小四倍。
这个公式很好地解释了为什么我们在远离汽车时听到的声音会比较小。
除了声压与距离的关系,我们还可以通过公式来计算声级。
声级是用来描述声音强度的物理量,一般用分贝(dB)来表示。
声级的计算公式如下:L = 20 log10(P / P0)。
其中,L表示声级,P表示声压,P0表示参考声压。
通过这个公式,我们可以将声压转换为声级。
在日常生活中,我们经常会遇到不同的噪音环境,例如交通噪音、工业噪音、家庭噪音等。
通过测量声压并将其转换为声级,我们可以更好地了解这些噪音对人体的影响。
除了声压与距离的关系,我们还可以通过公式来计算声级。
声级是用来描述声音强度的物理量,一般用分贝(dB)来表示。
声级的计算公式如下:L = 20 log10(P / P0)。
其中,L表示声级,P表示声压,P0表示参考声压。
通过这个公式,我们可以将声压转换为声级。
在日常生活中,我们经常会遇到不同的噪音环境,例如交通噪音、工业噪音、家庭噪音等。
为什么距离增加1倍声压级减少6dB?
声音在空中传播,以点为中心,呈球形状向外扩散,假设球的半径为1米,那么球的表面积= =4πr^2= 12.56平方米,如果半径增加一倍为2米,球的表面积= 4πr^2= 50.24平方米;
50.24/12.56 = 4,表示距离(半径)增加一倍表面积增加4倍。
如果此时功率不变,面积增加4倍,那单位面积的功率就只有原1/4(原来功率为1瓦,这1瓦的功率是分布在1平方米的面积上;现在功率还是1瓦,面积却变大为4平方米,那么这4平方米上每1平方米上的功率=1/4。
距离远了1倍,功率减少为原来的1/4。
用前面的程式计算:距离增加一倍声压级的变化= 10log(1/4) = -10*0.6021 = -6dB
经验:距离每增加一倍,声压级减少6dB。
标准计算距离与声压级的程式:分贝dB = 1米声压级-20*log距离
为什么是20log呢?此处可以看做:分贝dB = 1米声压级-10*log(距离的平方),因为功率正比于距离的平方。
例:1米处声压级= 102.5dB,40米处的声压级:102.5-20*log40 = 102.5-20*1.6021 = 70.5dB
综合:满功率300瓦,40米处的声压级计算:先计算1米满功率300瓦声压级(127.5dB),再套用"距离与声压级"程式= 127.5-20*log40 = 95.5dB
当年为了比较声音的大小,老贝先生(亚历山大·格雷厄姆·贝尔)用“log"中文称"对数函数",比如2W的声音这么大,那2W的就用log(2/1) = 0.3,后来他又说,有小数不方便,前面再乘10,于是声音大小的标准有了,分贝(dB)=10xlog(被测功率/基准功率),也就是说功率为2W时,其分贝比基准功率的分贝数大10*log(2/1)= 3dB
2瓦的功率其声音比1瓦的功率所产生的声音要大3dB
所以一个经验:功率每增加一倍,声压增加3dB。
标准计算功率与声压级的程式:分贝dB = 1瓦声压级+10*log功率
例:音箱1瓦声压级= 102.5dB,满功率300瓦的声压级计算:
300瓦声压级dB = 102.5+10xlog300 = 102.5+10*2.4772 = 127.5dB
总结:
功率增加一倍,声压级增加3dB
距离增加一倍,声压级减少6dB
用以下两个公式,就免了2、4、8、16的数指头算声压了
功率与声压级的程式:分贝dB = 1瓦声压级+10*log功率距离与声压级的程式:分贝dB = 1米声压级-20*log距离。