下载文档原格式
2012年高考真题理科数学解析汇编：立体几何参考答案2则B (2， 0, 0），C (2, 22,0），E (1， 2， 1）,)1,2,1(=AE ,)0,22,0(=BC设AE 与BC 的夹角为θ，则222224||||cos ===⨯⋅BC AE BC AE θ,θ=4π.由此可知，异面直线BC 与AE 所成的角的大小是4π [解法二］取PB 中点F ,连接EF 、AF ，则EF ∥BC ,从而∠AEF （或其补角)是异面直线 BC 与AE 所成的角在AEF ∆中，由EF =2、AF =2、AE =2 知AEF ∆是等腰直角三角形, 所以∠AEF =4π。
因此异面直线BC 与AE 所成的角的大小是4π1.解(1）1111224ABC S ∆=⨯⨯=,又1CC 为三棱锥1C MBC-的高,11111123346C MBC ABC V S CC -∆∴=⋅=⨯⨯= (2)//CD AB ，所以1C MB ∠或其补角为导面直线CD 与1MC 所成的角.连接1,BC AB ⊥平面11,BCC B AB BC ∴⊥,在1Rt MBC ∆中,11415,2BC MB =+==15tan 2512C MB ∠==,故1arctan 25C MB ∴∠=,即异面直线CD 与1MC 所成的角为arctan 252.解析:(1)证法一 如图，过直线b 上任一点作平面π的垂线n ，设直线,,,a b c n 的方向向量分别是,,,a b c n ，则,,b c n 共面，根据平面向量基本定理，存在实数,λμ使得c b n λμ=+ABCD P EF则()()()a c a b n a b a n λμλμ⋅=⋅+=⋅+⋅ 因为a b ⊥，所以0a b ⋅= 又因为aπ,n π⊥，所以0a n ⋅=故0a c ⋅=，从而a c ⊥证法二 如图,记c b A ⊥=,P 为直线b 上异于点A 的任意一点，过P 作PO π⊥，垂足为O ，则O c ∈ ∵PO π⊥，a π，∴直线PO a ⊥又a b ⊥，b平面PAO ,POb P =∴a ⊥平面PAO ，又c 平面PAO ，∴a c ⊥（2）逆命题:a 是平面π内一条直线，b 是π外的一条直线(b 不垂直于π)，c 是直线b 在π上的投影，若a c ⊥，则a b ⊥. 逆命题为真命题. 3. 解析：（Ⅰ)在等腰梯形ABCD 中,AB∥CD，∠DAB=60°，CB=CD,由余弦定理可知202223)180cos(2CD DAB CB CD CB CD BD =∠-⋅⋅-+=,即AD CD BD 33==，在ABD ∆中,∠DAB=60°,AD BD 3=,则ABD ∆为直角三角形,且DB AD ⊥.又AE⊥BD,⊂AD 平面AED ，⊂AE 平面AED ，且A AE AD = ，故BD⊥平面AED ； (Ⅱ)由(Ⅰ)可知CB AC ⊥,设1=CB ,则3==BD CA ，建立如图所示的空间直角坐标系，)0,21,23(),0,1,0(),01,0(-D B F ，向量)1,0,0(=n 为平面BDC 的一个法向量.设向量),,(z y x m =为平面BDF 的法向量,则⎪⎩⎪⎨⎧=⋅=⋅00FB m BD m ，即⎪⎩⎪⎨⎧=-=-002323z y y x , 取1=y ，则1,3==z x ,则)1,1,3(=m 为平面BDF 的一个法向量.zx y5551,cos ==⋅>=<nm n m n m ，而二面角F —BD —C 的平面角为锐角，则 二面角F-BD-C 的余弦值为55. 解法二:取BD 的中点G ，连接1,CG FG ，由于CB CD =，因此CG BD ⊥， 又FC ⊥平面ABCD ，BD ⊂平面ABCD ,所以FC BD ⊥ 由于,,FC CG C FC CG ⋂=⊂平面FCG ,所以BD ⊥平面FCG故BD FG ⊥，所以FGC ∠为二面角F BD C --的平面角.在等腰三角形BCD 中，由于120BCD ∠=︒，因为12CG CB=,又CB CF=，所以225GF CG CF CG =+=，故5cos 5FGC ∠=，因此二面角F BD C --的余弦值为55。
线性代数期末试卷一一、填空题（每小题3分）（4）设A 为n 阶矩阵，*||0,≠A A 为A 的伴随矩阵，E 为n 阶单位矩阵，若A 有特征值λ，则*2()+A E 必有特征值__________.解：2||1⎛⎫+ ⎪⎝⎭A λ.设0x ≠，使x x λ=A . 由*||⋅=A A A E 知，***||()x x x x ===A A A A A λλ. 由||0≠A 知≠λ0.**2**2||||,()()()x x x x x ===A A A A A A λλ，*22||[()][()1]x x ==+A A E λ，*2()+A E 有一特征值 2||1+A λ.二、选择题（每小题3分）（4）设矩阵111222333a b c a b c a b c ⎛⎫⎪⎪ ⎪⎝⎭是满秩的，则直线333121212x a y b z c a a b b c c ---==---与直线111232323x a y b z c a a b b c c ---==---.（A ）相交于一点； （B ）重合； （C ）平行但不重合； （D ）异面。
解：（A ）正确记 1111{,,}a b c =α 1111(,,)a b c =A 2222{,,}a b c =α 2222(,,)a b c =A 3333{,,}a b c =α 3333(,,)a b c =A因为矩阵111222333a b c a b c a b c ⎛⎫⎪⎪ ⎪⎝⎭是满秩的，故123,,ααα线性无关，所以112223,s s =-=-r r αααα线性无关，12//s s r r且23,,A A A 三点不共线，确定一平面π，记 1l 为直线333121212,x a y b z c a a b b c c ---==--- 2l 为直线111232323x a y b z c a a b b c c ---==---，则 1l 为过3A ，且平行12A A 的直线，所以1l π∈， 2l 为过1A ，且平行23A A 的直线，所以2l π∈，因为12//s s r r，12//l l ∴，且同在π上，故相交，所以（A ）正确，当然（B ）、（C ）、（D ）不正确.三、（本题满分5分） 求直线11:111x y z l --==-在平面:210x y z π-+-=上的投影直线0l 的方程，并求0l 绕y 轴旋转一周所成曲面的方程.解：将l 的标准方程改为一般方程为 1010x y y z --=⎧⎨+-=⎩过l 的平面束方程为：1(1)0x y y z --++-=λ 由投影关系1(1)20--+=λλ，解之2=-λ 所以过l 且垂直平面π的方程为 3210x y z --==故0l 的方程为2103210x y z x y z -+-=⎧⎨--+=⎩设点(,,)M x y z 为直线上的点111(,,)M x y z 所旋转而成的曲面上的点，则1y y =且= 即 222211x z x z +=+ （1） 由1M 在0l 上，故111210x y z -+-= （2） 1113210x y z --+= （3） （2）、（3）联立，将11,x z 由1y 表出有11112211(1)(1)22x y yz y y ==⎧⎪⎨=-=-⎪⎩ 代入（1）得： 222214(1)4y y x z +-=+ 所求曲面为2224174210x y z y -++-= 为单叶双曲面. 十、（本题满分6分） 已知二次曲面方程2222224x ay z bxy xz yz +++++= 可以经过正交变换x y P z ⎛⎫⎛⎫⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ξηζ化为椭圆柱面方程2244+=ηζ，求,a b 的值和正交矩阵P .解：由111111b b a ⎛⎫ ⎪⎪ ⎪⎝⎭ 与014⎛⎫⎪⎪ ⎪⎝⎭相似得11111114b b a------=-----λλλλλλ，解之得到3, 1.a b ==对应于特征值10=λ的单位特征向量为T1x =；对应于特征值11=λ的单位特征向量为T2x =；对应于特征值34=λ的单位特征向量为T3x =；因此P ⎛=⎝.十一、（本题满分4分）设A 是n 阶矩阵，若存在正整数k ，使线性方程组0k x =A 有解向量α，且10k -≠A α. 证明：向量组1,,,k -A A L ααα是线性无关的. 解：设有常数12,,,k L λλλ，使得112,k k -+++=A A L λαλαλα0则有1112(),k k k --+++=A A A L λαλαλα0从而有11.k -=A λα0由于10k -≠A α，所以1.=λ0类似可证得 230,k ====L λλλ因此向量组1,,,k -A A L ααα线性无关.十二、（本题满分5分） 已知线性方程组（I ）1111221,222112222,221122,220,0,0.n n n n n n n n n a x a x a x a x a x a x a x a x a x +++=⎧⎪+++=⎪⎨⎪⎪+++=⎩L L L L L的一个基础解系为T T T 11121,221222,212,2(,,,),(,,,),,(,,,)n n n n n n b b b b b b b b b L L L L . 试写出线性方程组（II ）1111221,222112222,221122,22000n n n n n n n n n b y b y b y b y b y b y b y b y b y +++=⎧⎪+++=⎪⎨⎪⎪+++=⎩L L L L L的通解，并说明理由.解：（II ）的通解为T T111121,2221222,2(,,,)(,,,)n n y c a a a c a a a =++L L L T 12,2(,,,)n n n n n c a a a +L ，其中12,,,n c c c L 为任意常数.理由：方程组（I ）、（II ）的系数矩阵分别记为,A B ，则由（I ）的已知基础解系可知T=AB 0，于是T T ()==BA AB 0，因此可知A 的n 向个向量的转置向量为（II ）的n 个解向量.由于B 的秩为n ，故（II ）的解空间维数为2n n n -=，又A 的秩为2n 与（I ）的解空间维数之差，即为n ，故A 的n 个行向量线性无关，从而它们的转置向量构成（II ）的一个基础解系，于是得到（II ）的上述通解。
2012年全国各地高考数学试题及解答分类汇编大全（11解析几何初步）一、选择题：1.(2012安徽文)若直线10x y -+=与圆22()2x a y -+=有公共点，则实数a 取值范围是（ ） ()A [3,1]-- ()B [1,3]- （C ） [3,1]- ()D (,3][1,)-∞-+∞ 【解析】选C圆22()2x a y -+=的圆心(,0)C a 到直线10x y -+=的距离为d则 1231d r a a ≤=⇔≤⇔+≤⇔-≤≤2. (2012福建文)直线x+y 2-2=0与圆x 2+y 2=4相交于A,B 两点，则弦AB 的长度等于A. B C.D.13. (2012广东文)在平面直角坐标系xOy 中，直线3450x y +-=与圆224x y += 相交于A 、B 两点，则弦AB 的长等于A. B. C.D . 13. B. 圆心(0,0)到直线3450x y +-=的距离1d ==，则222()32AB r d =-=，即AB =4. (2012湖北文)过点P （1,1）的直线，将圆形区域{（x ，y ）|x 2+y 2≤4}分两部分，使得这两部分的面积之差最大，则该直线的方程为( )A. x+y-2=0B. y-1=0C. x-y=0D. x+3y-4=05.A 【解析】要使直线将圆形区域分成两部分的面积之差最大，必须使过点P 的圆的弦长达到最小，所以需该直线与直线OP 垂直即可.又已知点(1,1)P ，则1OP k =,故所求直线的斜率为-1.又所求直线过点(1,1)P ，故由点斜式得，所求直线的方程为()11y x -=--，即20+-=x y .故选A.【点评】本题考查直线、线性规划与圆的综合运用，数形结合思想.本题的解题关键是通过观察图形发现当面积之差最大时，所求直线应与直线OP 垂直，利用这一条件求出斜率，进而求得该直线的方程.来年需注意直线与圆相切的相关问题.5、(2012江西理)在直角三角形ABC 中，点D 是斜边AB 的中点，点P 为线段CD 的中点，则222||||||PA PB PC +=（ ）A ．2B ．4C ．5D ．105. D 【解析】本题主要考查两点间的距离公式，以及坐标法这一重要的解题方法和数形结合的数学思想.不失一般性，取特殊的等腰直角三角形，不妨令4AC BC ==,则AB =,CD =12AB =,1||2PC PD CD ===PA PB ====,所以222||||101010||2PA PB PC ++==. 【点评】对于非特殊的一般图形求解长度问题，由于是选择题，不妨尝试将图形特殊化，以方便求解各长度，达到快速求解的目的.体现考纲中要求掌握两点间的距离公式.来年需要注意点到直线的距离公式.6.(2012辽宁文) 将圆x 2+y 2 -2x-4y+1=0平分的直线是（ ）（A ）x+y-1=0 （B ） x+y+3=0 （C ）x-y+1=0 （D ）x-y+3=0 【答案】C【解析】圆心坐标为（1，2），将圆平分的直线必经过圆心，故选C 【点评】本题主要考查直线和圆的方程，难度适中。
2012年全国统一高考数学试卷（理科）（大纲版）参考答案与试题解析一、选择题（共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．（5分）（2014•大庆二模）复数=（）的分子分母都乘以分母的共轭复数，得=或．C D．轴上，且椭圆的方程为4．（5分）已知正四棱柱ABCD﹣A 1B1C1D1中，AB=2，，E为CC1的中点，则直线AC1与平面BED的C DEC=×××BD=2BE=DE==2×=2×h=5．（5分）（2014•重庆三模）已知等差数列{a n}的前n项和为S n，a5=5，S5=15，则数列的前100项和为．C D．=∴==6．（5分）△ABC中，AB边的高为CD，若=，=，•=0，||=1，||=2，则=（）．C D．，进而可求，从而可求与解：∵•=0∵||=1||=2AB=∴∴∴7．（5分）（2014•宜春模拟）已知α为第二象限角，，则cos2α=（）D．=，两边平方得：=﹣，）×8．（5分）（2014•闸北区三模）已知F1、F2为双曲线C：x2﹣y2=2的左、右焦点，点P在C上，|PF1|=2|PF2|，则cos∠F1PF2=．C D．，==9．（5分）（2014•湖北）已知x=lnπ，y=log52，，则（），＞，即可得到答案．5=，=＞，即（311．（5分）将字母a，a，b，b，c，c排成三行两列，要求每行的字母互不相同，每列的字母也互不相同，则不同12．（5分）正方形ABCD的边长为1，点E在边AB上，点F在边BC上，，动点P从E出发沿直线向F运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角，当点P第一次碰到E时，P与正方形的边碰撞的CG=DH=二、填空题：本大题共4小题，每小题5分，共20分，把答案填在题中横线上．（注意：在试题卷上作答无效）13．（5分）若x，y满足约束条件则z=3x﹣y的最小值为﹣1．解：作出不等式组14．（5分）（2014•武汉模拟）当函数y=sinx﹣cosx（0≤x＜2π）取得最大值时，x=．﹣cosx cosx=2sinx cosx﹣﹣＜，=，x=．故答案为：）15．（5分）若的展开式中第3项与第7项的二项式系数相等，则该展开式中的系数为56．解：由题意可得，此时系数为16．（5分）三棱柱ABC﹣A1B1C1中，底面边长和侧棱长都相等，∠BAA1=∠CAA1=60°，则异面直线AB1与BC1所成角的余弦值为．=，，，∵∴（）﹣++=|==|===＜，=所成角的余弦值为三.解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．17．（10分）△ABC的内角A、B、C的对边分别为a、b、c，已知cos（A﹣C）+cosB=1，a=2c，求C．，sinAsinC=①sinC=18．（12分）如图，四棱锥P﹣ABCD中，底面ABCD为菱形，PA⊥底面ABCD，，PA=2，E是PC上的一点，PE=2EC．（Ⅰ）证明：PC⊥平面BED；（Ⅱ）设二面角A﹣PB﹣C为90°，求PD与平面PBC所成角的大小．，（2），﹣∴2，（，（）∴=﹣=0•=0），（的法向量为，则，=，则，﹣），∴•﹣b=∴，，（﹣，﹣＜，==19．（12分）乒乓球比赛规则规定：一局比赛，双方比分在10平前，一方连续发球2次后，对方再连续发球2次，依次轮换．每次发球，胜方得1分，负方得0分．设在甲、乙的比赛中，每次发球，发球方得1分的概率为0.6，各次发球的胜负结果相互独立．甲、乙的一局比赛中，甲先发球．（Ⅰ）求开始第4次发球时，甲、乙的比分为1比2的概率；（Ⅱ）ξ表示开始第4次发球时乙的得分，求ξ的期望．1，根据120．（12分）设函数f（x）=ax+cosx，x∈[0，π]．（Ⅰ）讨论f（x）的单调性；（Ⅱ）设f（x）≤1+sinx，求a的取值范围．，构造函数）x；②≤﹣时，∵，即x时，有时，，当时，≤≤21．（12分）已知抛物线C：y=（x+1）2与圆（r＞0）有一个公共点A，且在A处两曲线的切线为同一直线l．（Ⅰ）求r；（Ⅱ）设m，n是异于l且与C及M都相切的两条直线，m，n的交点为D，求D到l的距离．，到该切线的距离为，建立方程，求得，的斜率×=r=|MA|=到该切线的距离为∴﹣﹣﹣的距离为22．（12分）函数f（x）=x2﹣2x﹣3，定义数列{ x n}如下：x1=2，x n+1是过两点P（4，5），Q n（x n，f（x n））的直线PQ n与x轴交点的横坐标．（Ⅰ）证明：2≤x n＜x n+1＜3；（Ⅱ）求数列{ x n}的通项公式．的方程为时，可得，可得，可得是以﹣为首项，的方程为时，∴的方程为时，∴，∴，可得，∴∴∴是以﹣为首项，∴∴∴。
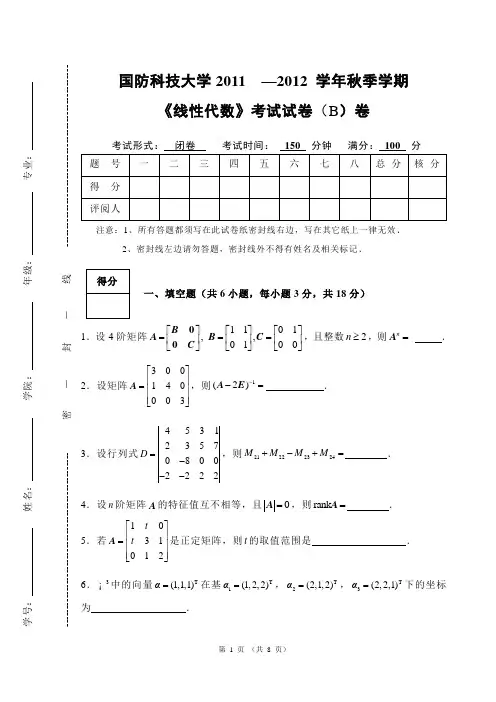
国防科技大学2011 —2012 学年秋季学期《线性代数》考试试卷（B ）卷注意：1、所有答题都须写在此试卷纸密封线右边，写在其它纸上一律无效．2、密封线左边请勿答题，密封线外不得有姓名及相关标记．一、填空题（共6小题，每小题3分，共18分）1．设4阶矩阵1101,,0100⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦B A BC C 00，且整数2n ≥，则n =A _ ． 2．设矩阵300140003⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦A ，则1(2)--=A E ． 3．设行列式4531235708002222D =---，则21222324M M M M +-+= ． 4．设n 阶矩阵A 的特征值互不相等，且0=A ，则rank =A ．5．若1031012t t ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦A 是正定矩阵，则t 的取值范围是 ． 6．3 中的向量T (1,1,1)=α在基T 1(1,2,2)=α，T 2(2,1,2)=α，T 3(2,2,1)=α下的坐标为 ．学号： 姓名： 学院： 年级： 专业：------------------------------------------------- 密 － 封 － 线 ---------------------------------------------------二、单选题（共6小题，每小题3分，共18分）1．设A 是三阶矩阵，将A 的第二行加到第一行上得到矩阵B ，将B 的第一列的-1倍加到第二列上得到矩阵C ，若1-=C P AP ，则=P 【 】 (A) 110010001-⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦． (B) 100110001⎡⎤⎢⎥-⎢⎥⎢⎥⎣⎦． (C) 110010001⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦． (D) 100110001⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦． 2．设n 阶矩阵,A B 的伴随矩阵分别为,**A B ，则分块矩阵⎡⎤⎢⎥⎣⎦A B 00的伴随矩阵为 【 】 (A) **⎡⎤⎢⎥⎣⎦A A B B 00． (B) **⎡⎤⎢⎥⎣⎦B B A A 00． (C) **⎡⎤⎢⎥⎣⎦A B B A 00． (D) **⎡⎤⎢⎥⎣⎦B A A B 00． 3．设三阶矩阵,A B 满足2--=A B A B E ，若101020201⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦A ，则B 等于 【 】 (A) 12-． (B) 12． (C) 1-． (D) 1．4．设A 是n 阶矩阵，b 是n 维列向量，若T rank rank ⎡⎤=⎢⎥⎣⎦A b A b 0，则 【 】 (A) =Ax b 有无穷多个解． (B) =Ax b 有唯一解．(C) T⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦A b x b y 00有非零解． (D) T ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦A b x b y 00仅有零解． 5．设n 维列向量组12(I):,,,m ααα 线性无关，且m n <，则n 维列向量组12(II):,,,m βββ 线性无关的充要条件是 【 】 (A) 向量组(I)可由向量组(II)线性表示．(B) 向量组(II)可由向量组(I)线性表示．(C) 向量组(I)与向量组(II)等价． (D) 矩阵12[]m ααα 与12[]m βββ 等价． 6．设12,λλ是n 阶矩阵A 的两个特征值，12,p p 分别为它们对应的特征向量，且 120λλ=-≠，则 【 】 (A) 12+p p 是A 的特征向量． (B) 12-p p 是A 的特征向量． (C) 12+p p 是2A 的特征向量． (D) 12+p p 不是2A 的特征向量．三、（10分）计算4阶行列式1111234549162560403024A ．号： 姓名： 学院： 年级： 专业： ----------------------------------------------- 密 － 封 － 线 -----------------------------------------------------四、（10分）设100011110,101111110⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦A B，E是三阶单位矩阵，解矩阵方程+=++AXA BXB AXB BXA E．学号： 姓名： 学院： 年级： 专业：------------------------------------------------- 密 － 封 － 线 ------------------------------------------------------五、（10分）设n 阶实矩阵A 有n 个两两正交的特征向量，证明A 是对称矩阵．问,a b 为何值时，(1) β不能由123,,ααα线性表示；(2) β能由123,,ααα唯一线性表示，并求出其表达式；(3) β能由123,,ααα线性表示，但表达式不唯一，并求出一般表达式．六、(10分) 设123120347110,,,011234b a ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥====⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦αααβ．学号： 姓名： 学院： 年级： 专业：------------------------------------------------- 密 － 封 － 线 ------------------------------------------------------七、（12分）设3阶实对称矩阵A 的秩为2，126λλ==是A 的二重特征值，T 1(1,1,0)=α，T 2(2,1,1)=α都是对应于特征值6的特征向量． (1) 求A 的另一特征值及其对应的特征向量；(2) 求矩阵A ．八、（12分）设n阶矩阵A满足，且234A A E，证明+=(1) rank(4)rank()nA E A E；++-=(2) A可对角化；(3) 2+A E逆，并求其逆．。
中 国 科 学 技 术 大 学 2005—2006学年第2学期考试试卷考试科目:线性代数 得分: 学生所在系:姓名:学号:一、判断题（30分，每小题6分）。
判断下列命题是否正确，并简要说明理由。
1. 三维空间向量c b,a,共面的充要条件是0det =⎪⎪⎪⎭⎫⎝⎛⋅⋅⋅⋅⋅⋅⋅⋅⋅c c b c a c c b b b a b c a b a a a 。
2. 设A 为n 阶实正交方阵，I 为n 阶单位阵，则I A 2-为可逆方阵。
3. 设n m ⨯阶非零实矩阵A 和B 满足0='B A ，则A 的行向量线性相关，并且B 的行向量也线性相关。
4. 设)(R M n 是n 阶实方阵全体按矩阵的加法与数乘运算构成的线性空间，则满足0tr =A 的n 阶实方阵A 的全体构成)(R M n 的子空间。
5. 设B A ,为方阵，且⎪⎪⎭⎫⎝⎛B A 是实正定对称方阵，则B A ,也是实正定对称方阵。
二、计算题（62分）。
1. （15分）b a ,为何值时，下列线性方程组有解？当有解时，求出该方程组的通解。
⎪⎪⎩⎪⎪⎨⎧=-+++=+++=-+++=++++bx x x x x x x x x a x x x x x x x x x x 54321543254321543213345362232312.3. （15分）设n 阶实方阵⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----=2112112O O A n ，求n A det 和14-A 。
4. （17分）设V 是由所有2阶实方阵构成的实线性空间。
在定义内积Y X Y X '=tr ),(后，V 成为一个欧氏空间。
现定义V 上的变换X X X '+ : A 。
（1）证明： A 是一个线性变换；（2）求 A 在基⎭⎬⎫⎩⎨⎧⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛1000,0100,0010,0001下的表示矩阵；（3）求 A 的所有特征值与特征向量；（4）求V 的一组标准正交基，使得 A 在此基下的表示矩阵为对角阵。
