幂函数基础知识及例题

高中数学必修一《幂函数》精选习题（含详细解析）一、选择题1.下列函数中,是幂函数的是( )A.y=2xB.y=2x3C.y=D.y=2x22.若幂函数y=(m2-3m+3)x m-2的图象不过原点,则m的取值范围为( )A.1≤m≤2B.m=1或m=2C.m=2D.m=13.函数y=x-2在区间上的最大值是( )A. B. C.4 D.-44若本题的条件不变,则此函数在区间上的最大值和最小值之和为多少?5.在下列函数中,定义域为R的是( )A.y=B.y=C.y=2xD.y=x-16函数y=|x(n∈N,n>9)的图象可能是( )7下列幂函数在(-∞,0)上为减函数的是( )A.y=B.y=x2C.y=x3D.y=8下列幂函数中过点(0,0),(1,1)且为偶函数的是( )A.y=B.y=x4C.y=x-2D.y=9.在同一坐标系内,函数y=x a(a≠0)和y=ax-的图象可能是( )二、填空题10幂函数f(x)=xα过点,则f(x)的定义域是.11若y=a是幂函数,则该函数的值域是.12若函数f(x)是幂函数,且满足=3,则f的值等于.13.设a=,b=,c=,则a,b,c的大小关系是.14已知幂函数f=(m∈Z)的图象与x轴,y轴都无交点,且关于原点对称,则函数f的解析式是.三、解答题15.比较下列各组数的大小:(1)1.10.1,1.20.1;(2)0.24-0.2,0.25-0.2;(3)0.20.3,0.30.3,0.30.2.16.已知幂函数y=x3-p(p∈N*)的图象关于y轴对称,且在(0,+∞)上为增函数,求满足条件(a+1<(3-2a的实数a的取值范围.17幂函数f的图象经过点(,2),点在幂函数g的图象上,(1)求f,g的解析式.(2)x为何值时f>g,x为何值时f<g?18已知幂函数f(x)=(m2-m-1)·x-5m-3在(0,+∞)上是增函数,又g(x)=lo(a>1).(1)求函数g(x)的解析式.(2)当x∈(t,a)时,g(x)的值域为(1,+∞),试求a与t的值.参考答案与解析1【解析】选C.由幂函数所具有的特征可知,选项A,B,D中x的系数不是1;故只有选项C中y==x-1符合幂函数的特征.2【解析】选D.由题意得解得m=1.3【解析】选C.y=x-2在区间上单调递减,所以x=时,取得最大值为4.4【解析】y=x-2在区间上单调递减,所以x=2时,取得最小值为,当x=时,取得最大值为4.故最大值和最小值的和为.5【解析】选C.选项A中函数的定义域为[0,+∞),选项B,D中函数的定义域均为(-∞,0)∪(0,+∞).6【解析】选C.因为y=|x为偶函数,所以排除选项A,B.又n>9,所以<1.由幂函数在(0,+∞)内幂指数小于1的图象可知,只有选项C符合题意.7【解析】选B.函数y=,y=x3,y=在各自定义域上均是增函数,y=x2在(-∞,0)上是减函数. 8【解析】选B.函数y=x4是过点(0,0),(1,1)的偶函数,故B正确;函数y=x-2不过点(0,0),故C 不正确;函数y=,y=是奇函数,故A,D不正确.9【解析】选C.当a<0时,函数y=ax-在R上是减函数,此时y=x a在(0,+∞)上也是减函数,同时为减的只有D选项,而函数y=ax-与y轴相交于点,此点在y轴的正半轴上,故D选项不适合.当a>0时,函数y=ax-在R上是增函数,与y轴相交于点,此点在y轴的负半轴上,只有A,C适合,此时函数y=x a在(0,+∞)上是增函数,进一步判断只有C适合.10【解析】因为幂函数f(x)过点,所以=2α,所以α=-1,所以f(x)=x-1=,所以函数f(x)的定义域是(-∞,0)∪(0,+∞).答案:(-∞,0)∪(0,+∞)11【解析】由已知y=a是幂函数,得a=1,所以y=,所以y≥0,故该函数的值域为[0,+∞).答案:[0,+∞)3,12【解析】依题意设f(x)=xα,则有=3,得α=log2则f(x)=,于是f====.答案:13【解析】因为y=在x∈(0,+∞)上递增,所以>,即a>c,因为y=在x∈(-∞,+∞)上递减,所以>,即c>b,所以a>c>b.答案:a>c>b14【解析】因为函数的图象与x轴,y轴都无交点,所以m2-1<0,解得-1<m<1;因为图象关于原点对称,且m∈Z,所以m=0,所以f=x-1.答案:f=x-115【解析】(1)由于函数y=x0.1在第一象限内单调递增,又因为1.1<1.2,所以1.10.1<1.20.1.(2)由于函数y=x-0.2在第一象限内单调递减,又因为0.24<0.25,所以0.24-0.2>0.25-0.2.(3)首先比较指数相同的两个数的大小,由于函数y=x0.3在第一象限内单调递增,而0.2<0.3,所以0.20.3<0.30.3.再比较同底数的两个数的大小,由于函数y=0.3x在定义域内单调递减,而0.2<0.3,所以0.30.3<0.30.2.所以0.20.3<0.30.3<0.30.2.16【解析】因为幂函数y=x3-p(p∈N*)的图象关于y轴对称,所以函数y=x3-p是偶函数.又y=x3-p在(0,+∞)上为增函数,所以3-p是偶数且3-p>0.因为p∈N*,所以p=1,所以不等式(a+1<(3-2a化为:(a+1<(3-2a.因为函数y=是[0,+∞)上的增函数,所以⇒⇒-1≤a<,故实数a的取值范围为.17【解析】(1)设f=xα,则()α=2,所以α=2,所以f=x2.设g=xβ,则(-2)β=,所以β=-2,所以g=x-2(x≠0).(2)从图象可知,当x>1或x<-1时,f>g;当-1<x<0或0<x<1时,f<g.18【解析】(1)因为f(x)是幂函数,且在(0,+∞)上是增函数,所以解得m=-1,所以g(x)=loga.(2)由>0可解得x<-1或x>1,所以g(x)的定义域是(-∞,-1)∪(1,+∞).又a>1,x∈(t,a),可得t≥1,设x1,x2∈(1,+∞),且x1<x2,于是x2-x1>0,x1-1>0,x2-1>0,所以-=>0, 所以>.由a>1,有loga >loga,即g(x)在(1,+∞)上是减函数.又g(x)的值域是(1,+∞),所以得g(a)=loga=1,可化为=a, 解得a=1±,因为a>1,所以a=1+,综上,a=1+,t=1.。

经典例题透析类型一、求函数解析式例1.已知幕函数y = (nr-m-])x,,,2-2m~3,当xw(0, + 8)时为减函数，则幕函数y二___________________ .解析：由于丁 =(加2—血—1)#宀2心为幕函数，所以m2— \ = \,解得m = 2 ,或m = —\.当ni = 2时，nr -2m-3 = -3 , y = x~3在(0, + 8)上为减函数；当m = -l时，/7?2-2m-3 = 0, y = %° =1(x^0)在(0, + «)上为常数函数，不合题意，舍去.故所求幕函数为y = x-3.总结升华：求慕函数的解析式，一般用待定系数法，弄明白需函数的定义是关键.类型二、比较幕函数值大小例2.比较下列各组数的大小.4 4 _ 3 _ 3(1)3」4万与兀了；(2)(-近门与(-73)^.4 4_4解：⑴由于幕函数y = •亍(x>0)单调递减且3」4 <龙，・・・3.14万 > 兀了._3(2)由于y =兀5这个幕函数是奇函数.・•・f (-x) =-f (x)—_ 3 _ 3 _ 3 _ 3 _ _因此，(一血门二一(血)V,(―巧)V =—(內)V ,而y = (x>0)单调递减，且血3 3 3 3 3 3・・・(血戸 >"门即(一血门v(总结升华.(1)各题中的两个数都是“同指数”的幕，因此可看作是同一个幕函数的两个不同的函数值，从而可根据幕函数的单调性做出判断.(2)题(2)中，我们是利用幕函数的奇偶性，先把底数化为正数的幕解决的问题.当然，若直接利用x<0 上幕函数的单调性解决问题也是可以的.举一反三【变式一】比较O.805, O.905, 0.9皿的大小.思路点拨:先利用幕函数)=兀"的增减性比较0・8°5与0.9°"的大小，再根据幕函数的图象比较0.9°"与0.9七5的大小.解：y = x Q-5^.(0, + oo)上单调递增，且0.8 v 0.9 ,.•,0.805 <0.905.作出函数y = X05与歹=兀七5在第一象限内的图彖，易知0.严< 0.9心.故 0.胛 vO.9°5 <0.9心.例3.已知幕函数y = f y = y = y = 在第一象限内的图象分别是G, C 2, C 3, G,（如图），则m, n 2, n ：“ m, 0, 1的大小关系？解:应为 ni<n 2<0<n 3<l<n4.总结升华：对于幕函数y = x a （aeR ）的图象，其函数性质的正确把握主要来源 于对图象的正确处理，而幕函数的图象，最重要的是搞清第一象限的图象类型及分布; 反过来，也能通过第一彖限的图彖判断指数的取值范围.举一反三ABC思路点拨：已知函数解析式和图像，可以用取点验证的方法判断.解:取W 则尸知*，选项B, D 符合；取归,则尸1,选项B 符合题意.类型三、求参数的范围例4•已知幕函数y = x m2（rneN ）的图象与兀y 轴都无交点，且关于y 轴对称，求加的值，并画出它 的图象.解：图象与上y 轴都无交点，/.zn-2<0,即m<2.又 m G N , m = 0/h2 .幕函数图彖关于y 轴对称，/. m = 0 ,或 m = 2 .当加=0时，函数为y = 图象如图1；图1图2举一反三 【变式一】若（a + l ）-2〉（3 —2d ）_2,求实数a 的取值范围.解法1:・・・仗+ 1）「2 >（3-2订2,考察y = 的图象，得以下四种可能情况:1总结升华.以上两种另法都是运用函数的单调性，但显然第二种方法更好.而这种方法的应用，必须对图象的特征 有深刻的认识.可见，能很好地运用数形结合是解决函数问题的重要途径.【变式二】当m 为何值时，幕函数y 二(n?-5m+6)丹5”-3的图象同时通过点(°, 0)和(1, 1).解：V y= (m 2-5m+6) x m ~2,n ~3 是幕函数..*.m 2-5m+6=l.得:m- ~ , 2又•・•函数图象过(0, 0)和(1, 1)点，.-.m 2-2m-3>0,得m>3或水-1,类型四、讨论函数性质例5.求函数y 二。

自主梳理1．幂函数的概念形如________的函数叫做幂函数，其中____是自变量，____是常数． 2．幂函数的性质(1)五种常见幂函数的性质，列表如下： 定义域 值域 奇偶性 单调性 过定点y ＝x R R 奇 Z (1,1)y ＝x 2 R [0，＋∞)偶 [0，＋∞)Z (－∞，0][y ＝x 3R R 奇 ZY ＝x 12[0，＋∞) [0，＋∞) 非奇 非偶 [0，＋∞)Z Y ＝x －1(－∞，0) ∪(0，＋∞)(－∞，0) ∪(0，＋∞)奇(－∞，0)[(0，＋∞)[(2)所有幂函数在________上都有定义，并且图象都过点(1,1)，且在第____象限无图象． (3)α>0时，幂函数的图象通过点____________，并且在区间(0，＋∞)上是________，α<0时，幂函数在(0，＋∞)上是减函数，图象______原点．1．已知幂函数y ＝f (x )的图像经过点⎝⎛⎭⎫4，12，则f (2)＝( ) A.14 B ．4C.22D. 2 2．下列函数中，其定义域与值域不同的函数是( ) A ．y ＝x 12B ．y ＝x －1 C ．y ＝x 13D ．y ＝x 23．已知f (x )＝x 12，若0<a <b <1，则下列各式中正确的是( )A ．f (a )<f (b )<f ⎝⎛⎭⎫1a <f ⎝⎛⎭⎫1b B ．f ⎝⎛⎭⎫1a <f ⎝⎛⎭⎫1b <f (b )<f (a ) C ．f (a )<f (b )<f ⎝⎛⎭⎫1b <f ⎝⎛⎭⎫1a D ．f ⎝⎛⎭⎫1a <f (a )<f ⎝⎛⎭⎫1b <f (b )4．已知f (x )＝x 2＋bx ＋c 且f (－1)＝f (3)，则( ) A ．f (－3)<c <f ⎝⎛⎭⎫52 B ．f ⎝⎛⎭⎫52<c <f (－3) C ．f ⎝⎛⎭⎫52<f (－3)<cD ．c <f ⎝⎛⎭⎫52<f (－3)5．(2013·蚌埠二中调研)设二次函数f (x )＝ax 2＋bx ＋c ，如果f (x 1)＝f (x 2)(x 1≠x 2)，则f (x 1＋x 2)＝( )A ．－b2aB ．－baC ．c D.4ac －b 24a6．若f (x )＝x 2－x ＋a ，f (－m )＜0，则f (m ＋1)的值( ) A ．正数 B ．负数 C ．非负数D ．与m 有关 7．对于函数y ＝x 2，y ＝x 12有下列说法：①两个函数都是幂函数；②两个函数在第一象限内都单调递增； ③它们的图像关于直线y ＝x 对称； ④两个函数都是偶函数； ⑤两个函数都经过点(0,0)、(1,1)； ⑥两个函数的图像都是抛物线型． 其中正确的有________．8．(2012·北京西城二模)已知函数f (x )＝x 2＋bx ＋1是R 上的偶函数，则实数b ＝________，不等式f (x －1)<x 的解集为________．9．(2012·无锡联考)设函数f (x )＝mx 2－mx －1，若f (x )<0的解集为R ，则实数m 的取值范围是________．10．如果幂函数f (x )＝x －12p 2＋p ＋32(p ∈Z)是偶函数．且在(0，＋∞)上是增函数．求p的值，并写出相应的函数f (x )的解析式．11．已知二次函数f(x)的图像过点A(－1,0)、B(3,0)、C(1，－8)．(1)求f(x)的解析式；(2)求f(x)在x∈[0,3]上的最值；(3)求不等式f(x)≥0的解集．12．设f(x)是定义在R上的偶函数，当0≤x≤2时，y＝x，当x>2时，y＝f(x)的图像是顶点为P(3,4)，且过点A(2,2)的抛物线的一部分．(1)求函数f(x)在(－∞，－2)上的解析式；(2)在下面的直角坐标系中直接画出函数f(x)的草图；(3)写出函数f (x )的值域．1．已知y ＝f (x )是偶函数，当x >0时，f (x )＝(x －1)2，若当x ∈⎣⎡⎦⎤－2，－12时，n ≤f (x )≤m 恒成立，则m －n 的最小值为( )A.13B.12 C.34D ．12．(2013·青岛质检)设f (x )与g (x )是定义在同一区间[a ，b ]上的两个函数，若函数y ＝f (x )－g (x )在x ∈[a ，b ]上有两个不同的零点，则称f (x )和g (x )在[a ，b ]上是“关联函数”，区间[a ，b ]称为“关联区间”．若f (x )＝x 2－3x ＋4与g (x )＝2x ＋m 在[0,3]上是“关联函数”，则m 的取值范围为________．3．(2012·滨州模拟)已知函数f (x )＝ax 2＋bx ＋c (a >0，b ∈R ，c ∈R)．(1)若函数f (x )的最小值是f (－1)＝0，且c ＝1，F (x )＝⎩⎪⎨⎪⎧f (x )，x >0，－f (x )，x <0，求F (2)＋F (－2)的值；(2)若a＝1，c＝0，且|f(x)|≤1在区间(0,1]上恒成立，试求b的取值范围．答 案 课时跟踪检测(九)A 级1．选C 设f (x )＝x α，因为图像过点⎝⎛⎭⎫4，12，代入解析式得：α＝－12， ∴f (2)＝2－12＝22.2．选D 对A ，定义域、值域均为[0，＋∞)；对B ，定义域、值域均为(－∞，0)∪(0，＋∞)；对C ，定义域值域均为R ；对D ，定义域为R ，值域为[0，＋∞)．3．选C 因为函数f (x )＝x 12在(0，＋∞)上是增函数，又0<a <b <1b <1a ，故f (a )<f (b )<f ⎝⎛⎭⎫1b <f ⎝⎛⎭⎫1a . 4．选D 由已知可得二次函数图像关于直线x ＝1对称，又f (－3)＝f (5)，c ＝f (0)＝f (2)，二次函数在区间(1，＋∞)上单调递增，故有f (－3)＝f (5)>f ⎝⎛⎭⎫52>f (2)＝f (0)＝c .5．选C 由题意得：a ≠0，x 1＋x 22＝－b 2a ，x 1＋x 2＝－b a .得f (x 1＋x 2)＝f ⎝⎛⎭⎫－b a ＝a ·b 2a 2－b 2a ＋c ＝c .6．选B 法一：∵f (x )＝x 2－x ＋a 的对称轴为x ＝12，而－m ，m ＋1关于12对称，∴f (m ＋1)＝f (－m )＜0.法二：∵f (－m )＜0，∴m 2＋m ＋a ＜0，∴f (m ＋1)＝(m ＋1)2－(m ＋1)＋a ＝m 2＋m ＋a ＜0. 7．①②⑤⑥8．解析：因为f (x )＝x 2＋bx ＋1是R 上的偶函数，所以b ＝0，则f (x )＝x 2＋1，解不等式(x －1)2＋1<x ，即x 2－3x ＋2<0得1<x <2.答案：0 {x |1<x <2}9．解析：若m ＝0，显然－1<0恒成立， 若m ≠0，则⎩⎨⎧m <0，Δ<0.∴－4<m <0.故所求范围为：－4<m≤0.答案：(－4,0]10．解：∵f(x)在(0，＋∞)上是增函数，∴－12＋p＋32>0，2p即p2－2p－3<0.∴－1<p<3.又∵f(x)是偶函数且p∈Z，∴p＝1，故f(x)＝x2.11．解：(1)由题意可设f(x)＝a(x＋1)(x－3)，将C(1，－8)代入得－8＝a(1＋1)(1－3)，得a＝2.即f(x)＝2(x＋1)(x－3)＝2x2－4x－6.(2)f(x)＝2(x－1)2－8，当x∈[0,3]时，由二次函数图像知，f(x)min＝f(1)＝－8，f(x)max＝f(3)＝0.(3)f(x)≥0的解集为{x|x≤－1，或x≥3}．12．解：(1)设顶点为P(3,4)且过点A(2,2)的抛物线的方程为y＝a(x－3)2＋4，将(2,2)代入可得a＝－2，则y＝－2(x－3)2＋4，即x>2时，f(x)＝－2x2＋12x－14.当x<－2时，即－x>2.又f(x)为偶函数，f(x)＝f(－x)＝－2×(－x)2－12x－14，即f(x)＝－2x2－12x－14.所以函数f(x)在(－∞，－2)上的解析式为f(x)＝－2x2－12x－14.(2)函数f(x)的图像如图，(3)由图像可知，函数f (x )的值域为(－∞，4]．B 级1．选D 当x <0时，－x >0，f (x )＝f (－x )＝(x ＋1)2， ∵x ∈⎣⎡⎦⎤－2，－12， ∴f (x )min ＝f (－1)＝0，f (x )max ＝f (－2)＝1， ∴m ≥1，n ≤0，m －n ≥1.2．解析：由题意知，y ＝f (x )－g (x )＝x 2－5x ＋4－m 在[0,3]上有两个不同的零点．在同一坐标系下作出函数y ＝m 与y ＝x 2－5x ＋4(x ∈[0,3])的图像如图所示，结合图像可知，当x ∈[2,3]时，y ＝x 2－5x ＋4∈⎣⎡⎦⎤－94，－2，故当m ∈⎝⎛⎦⎤－94，－2时，函数y ＝m 与y ＝x 2－5x ＋4(x ∈[0,3])的图像有两个交点．答案：⎝⎛⎦⎤－94，－2 3．解：(1)由已知c ＝1，a －b ＋c ＝0，且－b2a ＝－1，解得a ＝1，b ＝2.则f (x )＝(x ＋1)2.则F (x )＝⎩⎪⎨⎪⎧(x ＋1)2，x >0，－(x ＋1)2，x <0.故F (2)＋F (－2)＝(2＋1)2＋[－(－2＋1)2]＝8.(2)由题意得f (x )＝x 2＋bx ，原命题等价于－1≤x 2＋bx ≤1在(0,1]上恒成立，即b ≤1x －x且b ≥－1x－x 在(0,1]上恒成立．又当x ∈(0,1]时，1x －x 的最小值为0，－1x －x 的最大值为－2，故－2≤b ≤0.。

3.3 幂函数练习一、单选题1、已知幂函数f (x )＝kx α(k ∈R ，α∈R)的图象过点⎝⎛⎭⎫12，2，则k ＋α＝( A ) A ．12 B ．1 C ．32D ．22、下列函数中，既是偶函数，又在区间(0，＋∞)上单调递减的函数是( A ) A ．y ＝x－2B ．y ＝x－1C ．y ＝x 2D ．y ＝31x3、幂函数y ＝f (x )的图象过点(4,2)，则幂函数y ＝f (x )的图象是( C )4、幂函数()()2222m f x m m x -=--在()0,∞+上单调递减，则实数m 的值为（ A ） A ．1-B ．3C ．1-或3D ．3-5、若f (x )＝12x ，则不等式f (x )>f (8x －16)的解集是( A )A ．⎣⎡⎭⎫2，167B ．(0，2]C ．⎝⎛⎭⎫－∞，167 D ．[2，＋∞) 6、若幂函数f (x )＝()12255a a a x---在(0，＋∞)上单调递增，则a 等于( D )A ．1B ．6C ．2D ．－17、幂函数a b c d y x y x y x y x ====，，，在第一象限的图像如图所示，则a b c d ，，，的大小关系是 （ D ）A ．a b c d >>>B ．d b c a >>>C ．d c b a >>>D ．b c d a >>>8、已知幂函数y ＝p qx (p ，q ∈Z 且p ，q 互质)的图象关于y 轴对称，如图所示，则( D )A ．p ，q 均为奇数，且pq >0B ．q 为偶数，p 为奇数，且pq <0C ．q 为奇数，p 为偶数，且pq >0D ．q 为奇数，p 为偶数，且pq <0二、多选题9．下列关于幂函数y x α=的性质说法正确的有（ CD ） A ．当1α=-时，函数在其定义域上递减 B ．当0α=时，函数图象是一条直线 C ．当2α=时，函数是偶函数D ．当3α=时，函数的图象与x 轴交点的横坐标为0 10．已知函数()a f x x 的图象经过点1,33⎛⎫⎪⎝⎭则（ CD ）A ．()f x 的图象经过点(3,9)B ．()f x 的图象关于y 轴对称C ．()f x 在(0,)+∞上单调递减D ．()f x 在(0,)+∞内的值域为(0,)+∞11、已知幂函数f (x )＝()2231mm m m x +---，对任意x 1，x 2∈(0，＋∞)，且x 1≠x 2，都满足2121)()(x x x f x f -->0，若a ，b ∈R 且f (a )＋f (b )<0，则下列结论可能成立的有( BC )A ．a ＋b >0且ab <0B ．a ＋b <0且ab <0C ．a ＋b <0且ab >0D ．以上都可能12．若函数()f x x α=的定义域为R 且为奇函数，则α可能的值为（ BD ）A ．1-B ．1C ．2D ．3三、填空题13．若幂函数()21my m m x =--为偶函数，则m = ___2_____ .14、已知幂函数f (x )＝mx n ＋k 的图象过点⎝⎛⎭⎫116，14，则m －2n ＋3k ＝_____0__. 15、若()()21221112-+>+m m m ，则实数m 的取值范围是______⎣⎢⎡⎭⎪⎫5－12，2__________.16、给出下面四个条件：①f (m ＋n )＝f (m )＋f (n )；②f (m ＋n )＝f (m )·f (n )；③f (mn )＝f (m )·f (n )；④f (mn )＝f (m )＋f (n )．如果m ，n 是幂函数y ＝f (x )定义域内的任意两个值，那么幂函数y ＝f (x )一定满足的条件的序号为__③______． 四、解答题17．已知幂函数()f x x α=的图象经过点3,19⎛⎫ ⎪⎝⎭，求函数的解析式，并作出该函数图象的草图，判断该函数的奇偶性和单调性．解：因为幂函数()f x x α=的图象经过点3,19⎛⎫ ⎪⎝⎭，故可得139α=，解得2α=-，故()2f x x -=，其定义域为{|0}x x ≠，关于原点对称；其函数图象如下所示：数形结合可知，因为()f x 的图象关于y 轴对称，故其为偶函数； 且()f x 在()0,+∞单调递减，在(),0-∞单调递增.18、已知幂函数f (x )＝(m 2－5m ＋7)x －m －1(m ∈R)为偶函数．(1)求f ⎝⎛⎭⎫12的值；(2)若f (2a ＋1)＝f (a )，求实数a 的值． 解：(1)由m 2－5m ＋7＝1，得m ＝2或3. 当m ＝2时，f (x )＝x－3是奇函数，∴不满足题意，∴m ＝2舍去；当m ＝3时，f (x )＝x －4，满足题意， ∴f (x )＝x －4，∴f ⎝⎛⎭⎫12＝⎝⎛⎭⎫12－4＝16.(2)由f (x )＝x－4为偶函数和f (2a ＋1)＝f (a )可得|2a ＋1|＝|a |，即2a ＋1＝a 或2a ＋1＝－a ，∴a ＝－1或a ＝－13.19、已知幂函数f (x )＝21()mm x-+(m ∈N *)．(1)试确定该函数的定义域，并指明该函数在其定义域上的单调性；(2)若函数f (x )的图象经过点(2，2)，试确定m 的值，并求满足条件f (2－a )>f (a －1)的实数a 的取值范围．解：(1)因为m 2＋m ＝m (m ＋1)(m ∈N *)，而m 与m ＋1中必有一个为偶数，所以m 2＋m 为偶数， 所以函数f (x )＝21()m m x-+(m ∈N *)的定义域为[0，＋∞)，并且该函数在[0，＋∞)上为增函数．(2)因为函数f (x )的图象经过点(2，2)， 所以2＝2(m 2＋m )－12()12m m +-，即122＝2()12mm +-，所以m 2＋m ＝2，解得m ＝1或m ＝－2. 又因为m ∈N *，所以m ＝1，f (x )＝12x ， 又因为f (2－a )>f (a －1)， 所以⎩⎪⎨⎪⎧2－a ≥0，a －1≥0，2－a ＞a －1，解得1≤a ＜32，故函数f (x )的图象经过点(2，2)时，m ＝1.满足条件f (2－a )>f (a －1)的实数a 的取值范围为[1，32)．20、19．已知函数()()()2151Z m f x m m x m +=-+∈为幂函数，且为奇函数.(1)求m 的值，并确定()f x 的解析式； (2)令()()21g x f x x =++yg x 在1,12x ⎡⎤∈-⎢⎥⎣⎦的值域.解：(1)因为函数()()()2151Z m f x m m x m +=-+∈为幂函数，所以2511m m -+=，解得0m =或5m =， 当0m =时，函数()f x x =是奇函数，符合题意，当5m =时，函数()6f x x =是偶函数，不符合题意，综上所述，m 的值为0，函数()f x 的解析式为()f x x =. (2)由（1）知，()f x x =，所以()()2121g x f x x x x =+=++ 令21t x =+212t x -=，11,0123,032x x t -≤≤∴≤+≤∴≤≤ 所以2211()222t t g t t t -=+=+-，3t ⎡∈⎣， 根据二次函数的性质知，()g t 的对称轴为11122t =-=-⨯，开口向上，所以()g t 在3⎡⎣上单调递增；所以2min011()(0)0222g t g ==+-=-，(2max 31()(3)33122g t g === 所以函数()g x 在1,12⎡⎤-⎢⎥⎣⎦的值域为1312⎡⎤-⎢⎥⎣⎦.。

幂函数的概念例1、下列结论中，正确的是( )A．幂函数的图象都通过点(0,0)，(1,1) B．幂函数的图象可以出现在第四象限C．当幂指数α取1,3，12时，幂函数y＝xα是增函数D．当幂指数α＝－1时，幂函数y＝xα在定义域上是减函数解析当幂指数α＝－1时，幂函数y＝x－1的图象不通过原点，故选项A 不正确；因为所有的幂函数在区间(0，＋∞)上都有定义，且y＝xα (α∈R)，y>0，所以幂函数的图象不可能出现在第四象限，故选项B不正确；而当α＝－1时，y＝x－1在区间(－∞，0)和(0，＋∞)上是减函数，但它在定义域上不是减函数．答案 C例2、已知幂函数f(x)＝(t3－t＋1)x 15(7＋3t－2t2) (t∈Z)是偶函数且在(0，＋∞)上为增函数，求实数t的值．分析关于幂函数y＝xα(α∈R，α≠0)的奇偶性问题，设pq(|p|、|q|互质)，当q为偶数时，p必为奇数，y＝x pq是非奇非偶函数；当q是奇数时，y＝x pq的奇偶性与p的值相对应．解∵f(x)是幂函数，∴t3－t＋1＝1，∴t＝－1,1或0.当t＝0时，f(x)＝x75是奇函数；当t＝－1时，f(x)＝x25是偶函数；当t＝1时，f(x)＝x85是偶函数，且25和85都大于0，在(0，＋∞)上为增函数．故t＝1且f(x)＝x85或t＝－1且f(x)＝x25.点评如果题中有参数出现，一定要注意对参数的分类讨论，尤其对题中的条件t∈Z给予足够的重视．例3、如图是幂函数y ＝x m 与y ＝x n 在第一象限内的图象，则( )A ．-1<n<0<m<1B ．n <－1,0<m <1C ．－1<n <0，m >1D ．n <－1，m >1 解析 在(0,1)内取同一值x 0，作直线x ＝x 0，与各图象有交点，则“点低指数大”．如图，0<m <1，n <－1.答案 B点评 在区间(0,1)上，幂函数的指数越大，图象越靠近x 轴；在区间(1，＋∞)上，幂函数的指数越大，图象越远离x 轴．例4、已知x 2>x 13，求x 的取值范围．错解 由于x 2≥0，x 13∈R ，则由x 2>x 13，可得x ∈R .错因分析 上述错解原因是没有掌握幂函数的图象特征，尤其是y ＝x α在α>1和0<α<1两种情况下图象的分布．正解作出函数y=x2和y=31x 的图象(如右图所示)，易得x<0或x>1.例5、函数f (x )＝(m 2－m －1)xm 2＋m －3是幂函数，且当x ∈(0，＋∞)时，f (x )是增函数，求f (x )的解析式．分析 解答本题可严格根据幂函数的定义形式列方程求出m ，再由单调性确定m .解 根据幂函数定义得m 2－m －1＝1，解得m ＝2或m ＝－1，当m ＝2时，f (x )＝x 3在(0，＋∞)上是增函数；当m ＝－1时，f (x )＝x －3在(0，＋∞)上是减函数，不符合要求．故f (x )＝x 3.点评 幂函数y ＝x α (α∈R )，其中α为常数，其本质特征是以幂的底x 为自变量，指数α为常数(也可以为0)．这是判断一个函数是否为幂函数的重要依据和唯一标准．对本例来说，还要根据单调性验根，以免增根．变式 已知y ＝(m 2＋2m －2)x 1m 2－1＋2n －3是幂函数，求m ，n 的值．解由题意得⎩⎨⎧m 2＋2m －2＝1m 2－1≠02n －3＝0，解得⎩⎨⎧m ＝－3n ＝32，所以m ＝－3，n ＝32.例6、比较下列各组中两个数的大小：（1）535.1，537.1；（2）0.71.5，0.61.5；（3）32)2.1(－－，32)25.1(－－．解析：（1）考查幂函数y ＝53x 的单调性，在第一象限内函数单调递增， ∵1.5＜1.7，∴535.1＜537.1，（2）考查幂函数y ＝23x 的单调性，同理0.71.5＞0.61.5． （3）先将负指数幂化为正指数幂可知它是偶函数， ∵32)2.1(－－＝322.1－，32)25.1(－－＝3225.1－，又322.1－＞3225.1－， ∴32)2.1(－－＞3225.1－．点评：比较幂形式的两个数的大小，一般的思路是： （1）若能化为同指数，则用幂函数的单调性； （2）若能化为同底数，则用指数函数的单调性；（3）若既不能化为同指数，也不能化为同底数，则需寻找一个恰当的数作为桥梁来比较大小．例7、比较下列各组数的大小(1) 3－52与3.1－52；(2)－8－78与－⎝ ⎛⎭⎪⎫1978.分析 比较大小问题一般是利用函数的单调性，当不便利用单调性时，可用0与1去比较，这种方法叫“搭桥”法．解 (1)函数y ＝x －52在(0，＋∞)上为减函数，又3<3.1，所以3－52>3.1－52.(2)－8－78＝－⎝ ⎛⎭⎪⎫1878，函数y ＝x 78在(0，＋∞)上为增函数，又18>19，则⎝ ⎛⎭⎪⎫1878>⎝ ⎛⎭⎪⎫1978， 从而－8－78<－⎝ ⎛⎭⎪⎫1978.点评 比较大小的题，要综合考虑函数的性质，特别是单调性的应用，更善于运用“搭桥”法进行分组，常数0和1是常用的参数．变式 比较下列各组数的大小： (1)⎝ ⎛⎭⎪⎫－23－23与⎝ ⎛⎭⎪⎫－π6－23；(2)4.125，(－1.9)35与3.8－23.解 (1)⎝ ⎛⎭⎪⎫－23－23＝⎝ ⎛⎭⎪⎫23－23，⎝ ⎛⎭⎪⎫－π6－23＝⎝ ⎛⎭⎪⎫π6－23，∵函数y ＝x －23在(0，＋∞)上为减函数，又∵23>π6，∴⎝ ⎛⎭⎪⎫－23－23＝⎝ ⎛⎭⎪⎫23－23<⎝ ⎛⎭⎪⎫π6－23＝⎝ ⎛⎭⎪⎫－π6－23. (2)(4.1)25>125＝1,0<3.8－23<1－23＝1，(－1.9)35<0，所以(－1.9)35<3.8－23<(4.1)25.例8、 已知幂函数y ＝x 3m －9 (m ∈N *)的图象关于y 轴对称，且在(0，＋∞)上函数值随x 的增大而减小，求满足(a ＋1)－m 3<(3－2a )－m3的a 的范围．解 ∵函数在(0，＋∞)上递减， ∴3m －9<0，解得m <3， 又m ∈N *，∴m ＝1,2.又函数图象关于y 轴对称， ∴3m －9为偶数，故m ＝1，∴有(a ＋1)－13<(3－2a )－13.又∵y ＝x －13在(－∞，0)，(0，＋∞)上均递减，∴a ＋1>3－2a >0或0>a ＋1>3－2a 或a ＋1<0<3－2a ，解得23<a <32或a <－1.点评 (1)解决与幂函数有关的综合题时，一定要考虑幂函数的定义．(2)幂函数y ＝x α，由于α的值不同，单调性和奇偶性也就不同．变式 已知幂函数y ＝xm 2－2m －3 (m ∈Z )的图象与x 轴、y 轴都无公共点，且关于y 轴对称，求m 的值，且画出它的图象．解 由已知，得m 2－2m －3≤0，∴－1≤m ≤3. 又∵m ∈Z ，∴m ＝－1,0,1,2,3， 当m ＝0或m ＝2时，y ＝x －3为奇函数，其图象不关于y 轴对称，不符合题意． 当m ＝－1或m ＝3时，有y ＝x 0，其图象如图①所示． 当m ＝1时，y ＝x －4，其图象如图②所示．练习一、选择题 1．下列命题：①幂函数的图象都经过点(1,1)和点(0,0)；②幂函数的图象不可能在第四象限；③n ＝0时，y ＝x n 的图象是一条直线；④幂函数y ＝x n ，当n >0时，是增函数；⑤幂函数y ＝x n ，当n <0时，在第一象限内函数值随x 值的增大而减小． 其中正确的是( )A ．①和④B ．④和⑤C ．②和③D ．②和⑤ 答案 D2．下列函数中，不是幂函数的是( )A ．y ＝2xB ．y ＝x －1C ．y ＝xD ．y ＝x 2 答案 A3．设α∈⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫－2，－1，－12，13，12，1，2，3，则使f (x )＝x α为奇函数且在(0，＋∞)内单调递减的α值的个数是( )A ．1B ．2C ．3D ．4 答案 A 4．当x ∈(1，＋∞)时，下列函数图象恒在直线y ＝x 下方的偶函数是( )A ．y ＝x 12B ．y ＝x －2C ．y ＝x 2D ．y ＝x －1答案 B 5．如果幂函数y ＝(m 2－3m ＋3)·xm 2－m －2的图象不过原点，则m 的取值是( )A ．－1≤m ≤2B ．m ＝1或m ＝2C ．m ＝2D ．m ＝1 答案 B解析 由已知⎩⎨⎧m 2－3m ＋3＝1m 2－m －2≤0∴m ＝1或m ＝2.6．在函数y ＝1x2，y ＝2x 2，y ＝x 2＋x ，y ＝1 (x ≠0)中幂函数的个数为( )A ．1B ．0C ．2D ．3 答案 C解析 依据幂函数的定义判定，应选C.7．幂函数f (x )的图象过点⎝ ⎛⎭⎪⎫4，12，那么f (8)的值为( )A ．2 6B ．64 C.24 D.164答案 C解析 设f (x )＝x α (α为常数)，将⎝⎛⎭⎪⎫4，12点代入得12＝4α，∴α＝－12，f (x )＝x －12，∴f (8)＝8－12＝24.8．下列函数中，值域为[0，＋∞)的函数是( )A ．y ＝2xB ．y ＝x 2C ．y ＝x －2D ．y ＝log a x (a >0，且a ≠1) 答案 B解析 根据函数图象，选B. 二、填空题1．若幂函数y ＝f (x )的图象经过点⎝⎛⎭⎪⎫9，13，则f (25)＝_____________.答案 15解析 设f (x )＝x α，则9α＝13，α＝－12.∴f (25)＝25－12＝15.2．设幂函数y ＝x α的图象经过点(8,4)，则函数y ＝x α的值域是______________．答案 [0，＋∞)解析 由4＝8α，得α＝23，∴y ＝x 23≥0.3. 如图所示是幂函数y=x α在第一象限内的图象，已知α取±2，± 四个值，则相应于曲线C1，C2，C3，C4的α依次为 .答案 2，12，－12，－24．若幂函数y ＝f (x )的图象经过点(2，2)，则f (25)的值是________．答案 5解析 设y ＝x α，∵点(2，2)在y ＝x α的图象上，∴2＝2α，∴α＝12，∴f (x )＝x 12.故f (25)＝2512＝5.5．幂函数y ＝x α(α∈R )的图象一定不经过第________象限． 答案 四6．把下列各数223，⎝ ⎛⎭⎪⎫53－13，⎝ ⎛⎭⎪⎫－233，⎝ ⎛⎭⎪⎫150，⎝ ⎛⎭⎪⎫3223，按由小到大的排列顺序为__________________．答案 ⎝ ⎛⎭⎪⎫－233<⎝ ⎛⎭⎪⎫53－13<⎝ ⎛⎭⎪⎫150<⎝ ⎛⎭⎪⎫3223<223.7．已知幂函数f (x )＝x －12，若f (a ＋1)<f (10－2a )，则a 的取值范围是________．答案 3<a <5解析 f (x )＝x －12＝1x (x >0)，由图象知x ∈(0，＋∞)时为减函数，又f (a＋1)<f (10－2a )，∴⎩⎨⎧a ＋1>0，10－2a >0，a ＋1>10－2a .得⎩⎨⎧a >－1，a <5，a >3.∴3<a <5.三、解答题1．求函数y ＝52x ＋2x 51＋4（x ≥－32）值域．解析：设t ＝x 51，∵x ≥－32，∴t ≥－2，则y ＝t 2＋2t ＋4＝（t ＋1）2＋3． 当t ＝－1时，y min ＝3．∴函数y ＝52x ＋2x 51＋4（x ≥－32）的值域为［3，＋∞）．点评：这是复合函数求值域的问题，应用换元法．2．已知f (x )＝(m 2＋2m )·xm 2＋m －1，m 是何值时，f (x )是(1)正比例函数；(2)反比例函数；(3)二次函数；(4)幂函数．解 (1)若f (x )为正比例函数，则⎩⎨⎧m 2＋m －1＝1m 2＋2m ≠0，∴m ＝1. (2)若f (x )为反比例函数，则 ⎩⎨⎧m 2＋m －1＝－1m 2＋2m ≠0，∴m ＝－1. (3)若f (x )为二次函数，则⎩⎨⎧m 2＋m －1＝2m 2＋2m ≠0，∴m ＝－1±132. (4)若f (x )为幂函数，则m 2＋2m ＝1，∴m ＝－1±2。

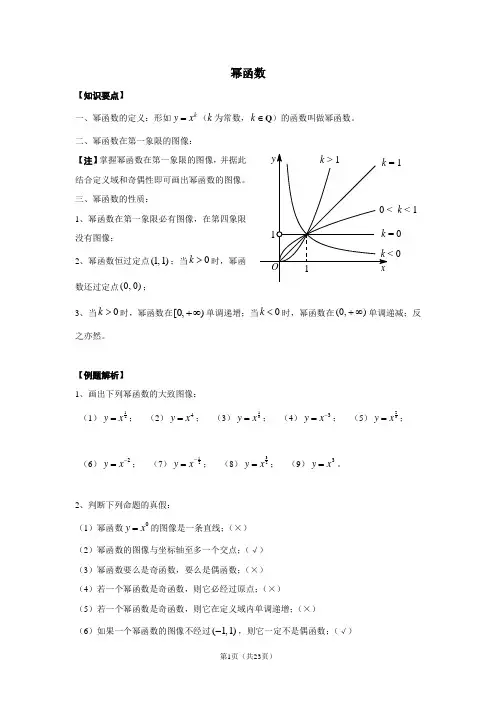
k < 1幂函数【知识要点】一、幂函数的定义：形如k x y =（k 为常数，∈k Q ）的函数叫做幂函数。

二、幂函数在第一象限的图像：【注】掌握幂函数在第一象限的图像，并据此结合定义域和奇偶性即可画出幂函数的图像。

三、幂函数的性质：1、幂函数在第一象限必有图像，在第四象限没有图像；2、幂函数恒过定点)1,1(；当0>k 时，幂函数还过定点)0,0(；3、当0>k 时，幂函数在),0[∞+单调递增；当0<k 时，幂函数在),0(∞+单调递减；反之亦然。

【例题解析】1、画出下列幂函数的大致图像：（1）21x y =； （2）4x y =； （3）31x y =； （4）3-=x y ； （5）32x y =；（6）2-=x y ； （7）21-=x y ； （8）23x y =； （9）3x y =。

2、判断下列命题的真假：（1）幂函数0x y =的图像是一条直线；（×） （2）幂函数的图像与坐标轴至多一个交点；（√） （3）幂函数要么是奇函数，要么是偶函数；（×） （4）若一个幂函数是奇函数，则它必经过原点；（×） （5）若一个幂函数是奇函数，则它在定义域内单调递增；（×）（6）如果一个幂函数的图像不经过)1,1(-，则它一定不是偶函数；（√）（7）如果两个幂函数的图像有三个公共点，那么这两个函数一定相同； （8）任何两个不同的幂函数的图像最多有三个交点。

（√）3、已知函数a x y =（∈a Q ）的图像当10<<x 时在直线x y =的上方，当1>x 时在直线x y =的下方，则a 的取值范围是}1|{Q ∈<a a a 且。

4、已知幂函数)237(3251)1(t t x t t y -+⋅+-=（∈t Z ）是偶函数，且在区间),0[∞+单调递增，求整数t 的值。

【解】由题意得：113=+-t t ，解得：0=t 或1=t 或1-=t ；当0=t 时，57x y =不是偶函数，所以0=t 不满足题意； 当1=t 时，58x y =是偶函数，所以1=t 满足题意； 当1-=t 时，52x y =是偶函数，所以1-=t 满足题意。

高中数学：幂函数练习及答案幂函数的概念1.若y＝x2，y＝（）x，y＝4x2，y＝x5＋1，y＝（x－1）2，y＝x，y＝a x（a＞1），上述函数中幂函数的个数为（）A.0B.1C.2D.32.幂函数f（x）＝x3m－5（m∈N）在（0，＋∞）上是减函数，且f（－x）＝f（x），则m等于（）A.0B.1C.2D.0或13.当x∈（0，＋∞）时，幂函数y＝（m2－m－1）·x－m－1为减函数，则实数m等于（）A. B.－1 C.2或－1 D.2求幂函数的解析式4.已知点（，）在幂函数y＝f（x）的图象上，则f（x）的表达式是（）A.f（x）＝3xB.f（x）＝x3C.f（x）＝x－2D.f（x）＝（）x5.已知幂函数y＝f（x）的图象经过点（16,4），则f（）的值为（）A.3B.C.D.幂函数的定义域和值域6.若函数f（x）＝，则函数y＝f（4x－3）的定义域是（）A.（－∞，＋∞）B.（－∞，）C.[，＋∞）D.（，＋∞）7.有四个幂函数：①f（x）＝x－1;②f（x）＝x－2;③f（x）＝x3；④f（x）＝.某同学研究了其中的一个函数，他给出这个函数的两个性质：（1）定义域是{x|x∈R，且x≠0}；（2）值域是{y|y∈R，且y≠0}.如果这个同学给出的两个性质都是正确的，那么他研究的函数是（）A.①B.②C.③D.④比较幂值的大小8.下列关系中正确的是（）A.<<B.<<C.<<D.<<9.设a＝0.60.6，b＝0.61.5，c＝1.50.6，则a、b、c的大小关系是（）A.a<b<cB.a<c<bC.b<a<cD.b<c<a幂函数的图像10.函数y＝的图象是（）A. B. C. D.11.函数y＝ax2＋a与y＝（a≠0）在同一坐标系中的图象可能是（）A. B. C. D.12.如图所示，幂函数y＝xα在第一象限的图象，比较0，α1，α2，α3，α4,1的大小（）A.α1<α3<0<α4<α2<1B.0<α1<α2<α3<α4<1C.α2<α4<0<α3<1<α1D.α3<α2<0<α4<1<α113.幂函数y＝x－1及直线y＝x，y＝1，x＝1将平面直角坐标系的第一象限分成八个“卦限”：①，②，③，④，⑤，⑥，⑦，⑧（如图所示），那么幂函数y＝的图象经过的“卦限”是（）A.④⑦B.④⑧C.③⑧D.①⑤幂函数的性质14.幂函数y＝xα，对于给定的有理数α，其定义域与值域相同，则此幂函数（）A.一定是奇函数B.一定是偶函数C.一定不是奇函数D.一定不是偶函数15.函数f（x）＝在[－1,1]上是（）A.增函数且是奇函数B.增函数且是偶函数C.减函数且是奇函数D.减函数且是偶函数16.函数y＝x－2在区间[，2]上的最大值是（）A. B.－1 C.4 D.－417.下列结论中，正确的是（）A.幂函数的图象都经过点（0,0），（1,1）B.幂函数的图象可以出现在第四象限C.当幂指数α取1,3，时，幂函数y＝xα是增函数D.当α＝－1时，幂函数y＝xα在其整个定义域上是减函数18.已知幂函数的图象过点（2，），则它的单调增区间为________.19.已知幂函数f（x）＝x3m－9（m∈N*）的图象与x轴、y轴都无公共点且关于y轴对称，求满足≤的a的取值范围.幂函数的综合应用20.已知幂函数f（x）＝x（2－k）（1＋k）（k∈Z）满足f（2）<f（3）.（1）求实数k的值，并写出相应的函数f（x）的解析式；（2）对于（1）中的函数f（x），试判断是否存在正数m，使函数g（x）＝1－mf（x）＋（2m－1）x在区间[0,1]上的最大值为5.若存在，求出m的值；若不存在，请说明理由.21.集合A是由具备下列性质的函数f（x）组成的：①函数f（x）的定义域是[0，＋∞）；②函数f（x）的值域是[－2,4）；③函数f（x）在[0，＋∞）上是增函数，试分别探究下列两小题：（1）判断函数f1（x）＝－2（x≥0）及f2（x）＝4－6·（）x（x≥0）是否属于集合A？并简要说明理由；（2）对于（1）中你认为属于集合A的函数f（x），不等式f（x）＋f（x＋2）<2f（x＋1）是否对于任意的x≥0恒成立？若不成立，为什么？若成立，请说明你的结论.答案1.若y＝x2，y＝（）x，y＝4x2，y＝x5＋1，y＝（x－1）2，y＝x，y＝a x（a＞1），上述函数中幂函数的个数为（）A.0B.1C.2D.3【答案】C【解析】由幂函数的定义知，y＝x2，y＝（）x，y＝4x2，y＝x5＋1，y＝（x－1）2，y＝x，y＝ax（a＞1）七个函数中，是幂函数的是y＝x2和y＝x，故选C.2.幂函数f（x）＝x3m－5（m∈N）在（0，＋∞）上是减函数，且f（－x）＝f（x），则m等于（）A.0B.1C.2D.0或1【答案】B【解析】因为f（x）＝x3m－5（m∈N）在（0，＋∞）上是减函数，所以3m－5<0，故m<.又因为m∈N，所以m＝0或m＝1，当m＝0时，f（x）＝x－5，f（－x）≠f（x），不符合题意；当m＝1时，f（x）＝x－2，f（－x）＝f（x），符合题意.综上知，m＝1.3.当x∈（0，＋∞）时，幂函数y＝（m2－m－1）·x－m－1为减函数，则实数m等于（）A. B.－1 C.2或－1 D.2【答案】D【解析】因当x∈（0，＋∞）时，幂函数y＝（m2－m－1）·x－m－1为减函数，所以m2－m－1＝1，且－m－1＜0，解得m＝2或－1，且m＞－1，即m＝2.故选D.4.已知点（，）在幂函数y＝f（x）的图象上，则f（x）的表达式是（）A.f（x）＝3xB.f（x）＝x3C.f（x）＝x－2D.f（x）＝（）x【答案】B【解析】幂函数f（x）＝xα的图象过点（，），所以＝（）α，解得α＝3，所以幂函数为f（x）＝x3，故选B.5.已知幂函数y＝f（x）的图象经过点（16，4），则f（）的值为（）A.3B.C.D.【答案】C【解析】∵幂函数y＝f（x）＝xα的图象经过点（16，4），∴16α＝4，解得α＝，∴f（x）＝，∴f（）＝＝.故选C.6.若函数f（x）＝，则函数y＝f（4x－3）的定义域是（）A.（－∞，＋∞）B.（－∞，）C.[，＋∞）D.（，＋∞）【答案】D【解析】幂函数f（x）＝＝，其定义域为（0，＋∞），∴4x－3>0，∴x>，∴函数y＝f（4x－3）的定义域是（，＋∞）.7.有四个幂函数：①f（x）＝x－1;②f（x）＝x－2;③f（x）＝x3；④f（x）＝.某同学研究了其中的一个函数，他给出这个函数的两个性质：（1）定义域是{x|x∈R，且x≠0}；（2）值域是{y|y∈R，且y≠0}.如果这个同学给出的两个性质都是正确的，那么他研究的函数是（）A.①B.②C.③D.④【答案】A【解析】对于①，具有（1）定义域是{x|x∈R，且x≠0}；（2）值域是{y|y∈R，且y≠0}.对于②，具有性质（1）定义域是{x|x∈R，且x≠0}；但不具有性质（2）值域是{y|y∈R，且y≠0}.对于③，不具有性质（1）定义域是{x|x∈R，且x≠0}；也不具有性质（2）值域是{y|y∈R，且y≠0}.对于④，不具有性质（1）定义域是{x|x∈R，且x≠0}；也不具有性质（2）值域是{y|y∈R，且y≠0}.故选A.8.下列关系中正确的是（）A.<<B.<<C.<<D.<<【答案】D【解析】由于幂函数y＝在（0，＋∞）上递增，因此<，又指数函数y＝（）x在（0，＋∞）上递减，因此<，故<<.故选D.9.设a＝0.60.6，b＝0.61.5，c＝1.50.6，则a、b、c的大小关系是（）A.a<b<cB.a<c<bC.b<a<cD.b<c<a【答案】C【解析】∵0.6∈（0，1），∴y＝0.6x是减函数，∴0.60.6>0.61.5，又y＝x0.6在（0，＋∞）是增函数，∴1.50.6>0.60.6，∴b<a<c，故选C.10.函数y＝的图象是（）A. B. C. D.【答案】A【解析】设y＝f（x）＝，f（－x）＝＝＝＝＝f（x），又函数f（x）的定义域为R，故f（x）为偶函数，即其图象关于y轴对称.又∵>0，∴f（x）在（0，＋∞）上为增函数，又∵>1，∴f（x）在第一象限的图象与函数y＝x2的图象相类似，故选A.11.函数y＝ax2＋a与y＝（a≠0）在同一坐标系中的图象可能是（）A. B. C. D.【答案】D【解析】当a＞0时，二次函数y＝ax2＋a的图象开口向上，且对称轴为x＝0，顶点坐标为（0，a），故排除A，C；当a＜0时，二次函数y＝ax2＋a的图象开口向下，且对称轴为x＝0，顶点坐标为（0，a），函数y＝的图象在第二、四象限，故选D.12.如图所示，幂函数y＝xα在第一象限的图象，比较0，α1，α2，α3，α4，1的大小（）A.α1<α3<0<α4<α2<1B.0<α1<α2<α3<α4<1C.α2<α4<0<α3<1<α1D.α3<α2<0<α4<1<α1【答案】D【解析】由图知取x＝2得0<<<1<<，∴α3<α2<0<α4<α1.又α1>1，0<α4<1，故选D.13.幂函数y＝x－1及直线y＝x，y＝1，x＝1将平面直角坐标系的第一象限分成八个“卦限”：①，②，③，④，⑤，⑥，⑦，⑧（如图所示），那么幂函数y＝的图象经过的“卦限”是（）A.④⑦B.④⑧C.③⑧D.①⑤【答案】D【解析】幂函数y＝的图象形状是上凸形，在经过（1，1）点以前在y＝x上方，而过了（1，1）点后在y ＝x下方，故可知y＝过①⑤“卦限”.14.幂函数y＝xα，对于给定的有理数α，其定义域与值域相同，则此幂函数（）A.一定是奇函数B.一定是偶函数C.一定不是奇函数D.一定不是偶函数【答案】D【解析】函数y＝的定义域和值域都是[0，＋∞），它既不是奇函数，也不是偶函数；函数y＝x3的定义域和值域都是R，它是奇函数；如果一个幂函数是偶函数，它的图象一定分布在第一和第二象限，它的值域是（0，＋∞）或[0，＋∞），与它的定义域不同，所以如果一个幂函数的定义域与值域相同，它一定不是偶函数，答案为D.15.函数f（x）＝在[－1，1]上是（）A.增函数且是奇函数B.增函数且是偶函数C.减函数且是奇函数D.减函数且是偶函数【答案】A【解析】因为f（－x）＝＝－＝－f（x），所以f（x）是奇函数.因为>0，f（x）＝在第一象限内是增函数，所以f（x）＝在[－1，1]上是增函数，综上可知，f（x）＝在[－1，1]上是增函数且是奇函数.16.函数y＝x－2在区间[，2]上的最大值是（）A. B.－1 C.4 D.－4【答案】C【解析】函数y＝x－2在区间[，2]上是减函数，所以x＝时，y取最大值，最大值是（）－2＝4.故选C.17.下列结论中，正确的是（）A.幂函数的图象都经过点（0，0），（1，1）B.幂函数的图象可以出现在第四象限C.当幂指数α取1，3，时，幂函数y＝xα是增函数D.当α＝－1时，幂函数y＝xα在其整个定义域上是减函数【答案】C【解析】当幂指数α＝－1时，幂函数y＝x－1的图象不经过原点，故A错误；因为所有的幂函数在区间（0，＋∞）上都有定义，且y＝xα>0，所以幂函数的图象不可能出现在第四象限，故B错误；当α>0时，y＝xα是增函数，故C正确；当α＝－1时，y＝x－1在区间（－∞，0），（0，＋∞）上是减函数，但在整个定义域上不是减函数，故D 错误，故选C.18.已知幂函数的图象过点（2，），则它的单调增区间为________.【答案】[0，＋∞）【解析】设幂函数的解析式为y＝xα，∵幂函数y＝f（x）的图象过点（2，），∴＝2α，解得α＝，∴y＝，所以其单调增区间为[0，＋∞）.19.已知幂函数f（x）＝x3m－9（m∈N*）的图象与x轴、y轴都无公共点且关于y轴对称，求满足≤的a的取值范围.【答案】由已知得3m－9≤0，∴m≤3.又∵幂函数f（x）的图象关于y轴对称，∴3m－9为偶数，又∵m∈N*，∴m＝1，3.当m＝1或m＝3时，有≤或（a＋1）－1≤（3－2a）－1.又∵y＝和y＝x－1在（－∞，0），（0，＋∞）上均单调递减，∴a＋1≥3－2a>0或0>a＋1≥3－2a或a＋1<0<3－2a，解得≤a＜或a＜－1.故a的取值范围是（－∞，－1）∪[，）.20.已知幂函数f（x）＝x（2－k）（1＋k）（k∈Z）满足f（2）<f（3）.（1）求实数k的值，并写出相应的函数f（x）的解析式；（2）对于（1）中的函数f（x），试判断是否存在正数m，使函数g（x）＝1－mf（x）＋（2m－1）x在区间[0，1]上的最大值为5.若存在，求出m的值；若不存在，请说明理由.【答案】（1）对于幂函数f（x）＝x（2－k）（1＋k）满足f（2）<f（3），因此（2－k）（1＋k）>0，解得－1<k<2.因为k∈Z，所以k＝0或k＝1.当k＝0时，f（x）＝x2，当k＝1时，f（x）＝x2，综上所述，k的值为0或1，f（x）＝x2.（2）函数g（x）＝1－mf（x）＋（2m－1）x＝－mx2＋（2m－1）x＋1，由于要求m>0，因此抛物线开口向下，对称轴方程为x ＝，当m>0时，＝1－<1，因为在区间[0，1]上的最大值为5，所以或解得m ＝＋，满足题意.21.集合A是由具备下列性质的函数f（x）组成的：①函数f（x）的定义域是[0，＋∞）；②函数f（x）的值域是[－2，4）；③函数f（x）在[0，＋∞）上是增函数，试分别探究下列两小题：（1）判断函数f1（x ）＝－2（x≥0）及f2（x）＝4－6·（）x（x≥0）是否属于集合A？并简要说明理由；（2）对于（1）中你认为属于集合A的函数f（x），不等式f（x）＋f（x＋2）<2f（x＋1）是否对于任意的x≥0恒成立？若不成立，为什么？若成立，请说明你的结论.【答案】（1）函数f1（x ）＝－2不属于集合A.因为f1（x）的值域是[－2，＋∞），所以函数f1（x）＝－2不属于集合A.f2（x）＝4－6·（）x（x≥0）在集合A中，因为①函数f2（x）的定义域是[0，＋∞）；②f2（x）的值域是[－2，4）；③函数f2（x）在[0，＋∞）上是增函数.（2）∵f（x）＋f（x＋2）－2f（x＋1）＝6·（）x （－）<0，∴不等式f（x）＋f（x＋2）<2f（x＋1）对任意的x≥0恒成立.11/11。

3.3幂函数【知识梳理】知识点一幂函数的概念一般地，函数y ＝x α叫做幂函数，其中x 是自变量，α是常数．知识点二五个幂函数的图象与性质1．在同一平面直角坐标系内函数(1)y ＝x ；(2)y ＝12x ；(3)y ＝x 2；(4)y ＝x －1；(5)y ＝x 3的图象如图．2．五个幂函数的性质y ＝xy ＝x 2y ＝x 312y xy ＝x－1定义域R R R [0，＋∞){x |x ≠0}值域R [0，＋∞)R [0，＋∞){y |y ≠0}奇偶性奇偶奇非奇非偶奇单调性增在[0，＋∞)上增，在(－∞，0]上减增增在(0，＋∞)上减，在(－∞，0)上减知识点三一般幂函数的图象特征1．所有的幂函数在(0，＋∞)上都有定义，并且图象都过点(1,1)．2．当α>0时，幂函数的图象通过原点，并且在区间[0，＋∞)上是增函数．特别地，当α>1时，幂函数的图象下凸；当0<α<1时，幂函数的图象上凸．3．当α<0时，幂函数的图象在区间(0，＋∞)上是减函数．4．幂指数互为倒数的幂函数在第一象限内的图象关于直线y ＝x 对称．5．在第一象限作直线x ＝a (a >1)，它同各幂函数图象相交，按交点从下到上的顺序，幂指数按从小到大的顺序排列．【基础自测】1．下列函数中不是幂函数的是________．①y ＝x 0；②y ＝x 3；③y ＝2x ；④y ＝x －1.2．幂函数a b c d y x y x y x y x ====，，，在第一象限的图像如图所示，则a b c d ，，，的大小关系是（）A ．a b c d >>>B ．d b c a >>>C ．d c b a >>>D ．b c d a>>>3．已知幂函数f (x )＝k ·x αk ＋α等于()A.12B ．1C.32D ．24．函数()12f x x -=的定义域为_______，值域为___________．5．已知幂函数()()221m f x m m x +=-+是奇函数，则m =___________.【例题详解】一、幂函数的概念例1(1)给出下列函数：①31y x=；②32y x =-；③42y x x =+；④y =；⑤()21y x =-；⑥0.3x y =，其中是幂函数的有（）A ．1个B ．2个C ．3个D ．4个(2)已知幂函数()(R,R)f x k x k αα=⋅∈∈的图象经过点(14,2)，则k α+=（）A ．12B ．1C ．32D ．2(3)若幂函数()25ay a a x =--的图像关于y 轴对称，则实数=a ______．跟踪训练1(1)下列函数是幂函数的是（）A ．22y x =B ．1y x -=-C ．31y x =D ．2xy =(2)（多选）如果幂函数()22233mm y m m x--=-+的图象不过原点，则实数m 的取值为（）A ．0B ．2C ．1D ．无解(3)已知幂函数()2232(1)mm f x m x -+=-在()0+∞，上单调递增，则()f x 的解析式是_____.二、幂函数的图象及应用例2(1)如图，下列3个幂函数的图象，则其图象对应的函数可能是（）A ．①1y x -=，②12y x =，③13y x =B ．①1y x -=，②13y x =，③12y x =C ．①13y x =，②12y x =，③1y x -=D ．①13y x =，②1y x -=，③12y x =(2)函数()12f x x -=的大致图象是（）A ．B ．C ．D ．跟踪训练2(1)图中C 1、C 2、C 3为三个幂函数y x α=在第一象限内的图象，则解析式中指数α的值依次可以是（）A ．12、3、1-B ．1-、3、12C ．12、1-、3D ．1-、12、3(2)在同一坐标系内，函数(0)a y x a =≠和1y ax a=+的图象可能是()A ．B ．C ．D ．三、比较幂值的大小例3(1)1.5－3.1，23.1，2－3.1的大小关系是（）A ．23.1＜2－3.1＜1.5－3.1B ．1.5－3.1＜23.1＜2－3.1C ．1.5－3.1＜2－3.1＜23.1D ．2－3.1＜1.5－3.1＜23.1(2)下列比较大小中正确的是（）A ．0.50.53223⎛⎫⎛⎫< ⎪⎪⎝⎭⎝⎭B ．112335--⎛⎫⎛⎫-<- ⎪ ⎪⎝⎭⎝⎭C ．3377(2.1)(2.2)--<-D ．44331123⎛⎫⎛⎫-< ⎪ ⎪⎝⎭⎝⎭跟踪训练3(1)设1313a ⎛⎫= ⎪⎝⎭，1325b ⎛⎫= ⎪⎝⎭，12c =，则（）A ．a b c<<B ．c a b<<C ．b c a<<D ．b a c<<(2)已知0.325a ⎛⎫= ⎪⎝⎭，0.313b ⎛⎫= ⎪⎝⎭，0.313c -⎛⎫= ⎪⎝⎭，则a ，b ，c 的大小关系为（）A ．a c b<<B ．a b c<<C ．b<c<aD ．b a c<<四、幂函数性质的应用例4(1)若幂函数f （x ）的图象过点（16，8），则f （x ）<f （x 2）的解集为（）A ．（–∞，0）∪（1，+∞）B ．（0，1）C ．（–∞，0）D ．（1，+∞）(2)已知12()3f x x =，若01a b <<<，则下列各式中正确的是（）．A ．11()()f a f b f f a b ⎛⎫⎛⎫<<<⎪ ⎪⎝⎭⎝⎭B ．11()()f f f b f a a b ⎛⎫⎛⎫<<< ⎪ ⎪⎝⎭⎝⎭C ．11()()f a f b f f b a ⎛⎫⎛⎫<<<⎪ ⎪⎝⎭⎝⎭D ．11()()f f a f f b a b ⎛⎫⎛⎫<<< ⎪ ⎪⎝⎭⎝⎭(3)已知函数355()3f x x =，若当()0,x ∈+∞时，()0a f x f x ⎛+-> ⎝恒成立，则实数a 的取值范围是（）A ．()0,∞+B ．(),2-∞C ．()3,+∞D ．(),1-∞跟踪训练4(1)对于幂函数45()=f x x ，若0<a <b ，则2+⎛⎫⎪⎝⎭a b f ，()()2f a f b +的大小关系是________．(2)已知幂函数的图象经过点1(,22，那么()f x 的解析式为____________；不等式()2f x ≤的解集为____________.(3)已知幂函数39m y x -=（*m N ∈）的图象关于y 轴对称，且在(0,)+∞上是减函数．（i ）求m 的值；（ii ）求满足不等式33(1)(32)m m a a +<-的实数a 的取值范围．【课堂巩固】1．下列幂函数中，既是偶函数，又在区间(0，＋∞)上单调递减的是()A ．y ＝x－2B ．y ＝x－1C ．y ＝x 2D ．y ＝13x2．函数y =的图象大致为（）A ．B ．C ．D ．3．（多选）下列关于幂函数说法不正确的是（）A ．一定是单调函数B ．可能是非奇非偶函数C ．图像必过点(1,1)D ．图像不会位于第三象限4．对幂函数y x α=，填空：（1）当1α>，0x ≥时，图象恒过______和______两点；其中当01x <<时，幂函数图象在y x =图象的______方；当1x >时，幂函数图象在y x =图象的______方．（2）当01α<<，0x ≥时，图象也恒过______和______两点；其中当01x <<时，幂函数图象在y x =图象的______方；当1x >，幂函数图象在y x =图象的______方．（3）当0α<，0x >时，图象恒过点______．5．幂函数()()222mm m f x x =+-在区间()0,∞+上单调递减，则实数m 的值为______．6．已知2.4α>2.5α，则α的取值范围是________．7．已知幂函数()()211m f x m m x +=--是奇函数，则实数m 的值为________.8．已知幂函数1101 ()f x x ⎛⎫= ⎪⎝⎭，若()()182f a f a -<-，则a 的取值范围是__________.9．比较下列各组数的大小：(1)33()(2 2.5)----，；(2)788-，7819⎛⎫ ⎪⎝⎭.10．已知幂函数()()222322N mm y k k xm --*=--⋅∈的图象关于y 轴对称，且在()0,∞+上是减函数.(1)求m 和k 的值；(2)求满足()()132mma a --+<-的a 的取值范围.11．已知幂函数()y f x =的表达式为223()(21)()n n f x m x n -++=-∈Z ，函数()y f x =的图像关于y 轴对称，且满足(3)(5)f f <，求m n +的值．12．已知幂函数f (x )＝(m 2－5m ＋7)x m －1为偶函数．(1)求f (x )的解析式；(2)若g (x )＝f (x )－ax －3在[1,3]上不是单调函数，求实数a 的取值范围．【课时作业】1．“当()0,x ∈+∞时，幂函数()22231m m y m m x --=--为减函数”是“1m =-或2”的（）条件A ．既不充分也不必要B ．必要不充分C ．充分不必要D ．充要2．已知幂函数122()(32)m f x m m x -=-满足(2)(3)f f >，则m =（）A ．23B ．13-C ．1D ．1-3．函数23y x =的大致图象是（）A ．B ．C ．D ．4．给出幂函数：①()f x x =；②2()f x x =；③()3f x x =；④()f x =⑤()1f x x=．其中满足条件()()()121221022f x f x x x f x x ++⎛⎫>>> ⎪⎝⎭的函数的个数是（）A ．1B ．2C ．3D ．45．幂函数y =f （x ）的图象经过点（4，2），若0<a <b <1，则下列各式正确的是（）A ．f （a ）<f （b ）<f （1b ）1f a ⎛⎫< ⎪⎝⎭B ．11f f a b ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭<f （b ）<f （a ）C ．f （a ）<f （b ）11f f a b ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭D ．()()11f f a f f b a b ⎛⎫⎛⎫<<< ⎪ ⎪⎝⎭⎝⎭6．在同一直角坐标系中，二次函数2y ax bx =+与幂函数(0)ba y x x =>图像的关系可能为（）A ．B ．C ．D ．7．已知幂函数a y x =与b y x =的部分图像如图所示，直线2x m =，()01x m m =<<与a y x =，b y x =的图像分别交于A ，B ，C ，D 四点，且AB CD =，则a b m m +=（）A ．12B ．1C D ．28．函数()()2231mm f x m m x +-=--是幂函数，对任意()12,0,,x x ∈+∞，且12x x ≠，满足()()12120f x f x x x ->-，若,a b R ∈，且0,0a b ab +><，则()()f a f b +的值（）A ．恒大于0B ．恒小于0C ．等于0D ．无法判断9．（多选）已知幂函数()()2m f x m x =-，则（）A ．3m =B ．定义域为[)0,∞+C ．(1.5)(1.4)m m -<-D 2=10．（多选）下列说法正确的是（）A ．若幂函数的图象经过点1(,2)8，则解析式为13y x -=B ．若函数()45f x x -=，则()f x 在区间(,0)-∞上单调递减C ．幂函数y x α=()0α>始终经过点(0,0)和()1,1D ．若幂函数()()2223m f x m m x =--图象关于y 轴对称，则()()2253f a a f -+->11．已知幂函数()()2133a f x a a x +=-+为偶函数，则实数a 的值为__________.12．不等式()()2233213x x +<-的解为______.13．已知幂函数()f x 的图象过点⎛ ⎝⎭，且()()212f b f b -<-，则b 的取值范围是______.14．已知幂函数()f x 经过点(9,3)，则不等式()211f x x -+<的解集为___________．15．已知幂函数()()35m f x xm N -=∈在(0，＋∞)上是减函数，且f(－x)＝f(x)，求m 的值．16．已知幂函数f （x ）=()12-+m m x （m ∈N *）的图象经过点(2．（1）试求m 的值，并写出该幂函数的解析式；（2）试求满足f （1+a ）>f （a 的取值范围．17．已知幂函数()()2133m f x m m x +=-+为偶函数.(1)求幂函数()f x 的解析式；(2)若函数()()1f x g x x+=，根据定义证明()g x 在区间()1,+∞上单调递增.18．已知幂函数22+1()=(2+2)m f x m m x -在(0,)+∞上是减函数(1)求()f x 的解析式(2)若f f <，求a 的取值范围.。

答案B例3、比较下列各组中两个数的大小：（1）31.55，31.75；（2）0.71.5，0.61.5；（3）－2(－1.2)3，例题精选例1、下列结论中，正确的是()A ．幂函数的图象都通过点(0,0)，(1,1)B ．幂函数的图象可以出现在第四象限1例2、如图是幂函数y ＝x m 与y ＝x n 在第一象限内的图象，则C ．当幂指数α取1,3，2时，幂函数y ＝x α是增函数答案D ．当幂指数α＝－1时，幂函数y ＝x α在定义域上是减函数解析当幂指数α＝－1时，幂函数y ＝x －1的图象不通过原点，故选项A 不正确；因为所有的幂函数在区间(0，＋∞)上都有定义，且y ＝x α(α∈R )，y >0，所以幂函数的图象不可能出现在第四象限，故选项B 不正确；而当α＝－1时，y ＝x －1在区间(－∞，0)和(0，＋∞)上是减函数，但它在定义域上不是减函数．C(A ．-1<n<0<m<1B ．n <－1,0<m <1C ．－1<n <0，m >1D ．n <－1，m >1解析在(0,1)内取同一值x 0，作直线x ＝x 0，与各图象有交点，则“点低指数大”．如图，0<m <1，n<－1.－2(－1.25)3．解析：（1）考查幂函数y ＝3x 5的单调性，在第一象限内函数单调递增，∵1.5＜1.7，∴31.55＜31.75，（2）考查幂函数y ＝3x 2的单调性，同理0.71.5＞0.61.5．（3）先将负指数幂化为正指数幂可知它是偶函数，∵－2(－1.2)3＝－21.23，－2(－1.25)3＝－21.253，又－21.23＞ －21.253，∴－2(－1.2)3＞－21.253．点评：比较幂形式的两个数的大小，一般的思路是：（1）若能化为同指数，则用幂函数的单调性；（2）若能化为同底数，则用指数函数的单调性；（3）若既不能化为同指数，也不能化为同底数，则需寻找一个恰当的数作为桥梁来比较大小．例4（选做）、函数且y a a a a =2x +2x -1(>0≠1)在区间[-1，1]上有最大值14，则a 的值是_______．分析：令t =a x 可将问题转化成二次函数的最值问题，需注意换元后t 的取值范围．解：令t =a x ，则t >0，函数y =a 2x +2a x -1可化为y =(t +1)2-2，其对称轴为t =-1．∴当a >1时，∵x ∈-[1，1]，∴a ≤a x a 1≤，即a 1≤t ≤a ．∴当t =a 时，y max =(a +1)2-2=14．解得a =3或a =-5（舍去）；当<<a 01时，∵，∈-x 11][，∴≤≤a a a x 1，即≤≤aa t 1，∴ =a t 1时，⎝⎭⎪=+-=⎛⎫a y 12141max 2， 解得=a 31或=-a 51（舍去），∴a 的值是3或31．评注：利用指数函数的单调性求最值时注意一些方法的运用，比如：换元法，整体代入等．例5、求下列函数的定义域：（1）=a y x log 2； （2）=-a y x log (4)； （3）=-a y x 2log (9)． 分析：此题主要利用对数函数=log a y x 的定义域+∞(0,)求解。

1．一般地，______________叫做幂函数，其中x是自变量，α是常数．2．在同一平面直角坐标系中，画出幂函数y＝x，y＝x 2，y＝x3，y＝12x，y＝x－1的图象．3．结合2中图象，填空．(1)所有的幂函数图象都过点________，在(0，＋∞)上都有定义．(2)若α>0时，幂函数图象过点____________，且在第一象限内______；当0<α<1时，图象上凸，当α>1时，图象______．(3)若α<0，则幂函数图象过点________，并且在第一象限内单调______，在第一象限内，当x从＋∞趋向于原点时，函数在y轴右方无限地逼近于y轴，当x趋于＋∞时，图象在x轴上方无限逼近x轴．(4)当α为奇数时，幂函数图象关于______对称；当α为偶数时，幂函数图象关于______对称．(5)幂函数在第____象限无图象．一、选择题1．下列函数中不是幂函数的是()A．y＝x B．y＝x3C．y＝2x D．y＝x－12．幂函数f(x)的图象过点(4，12)，那么f(8)的值为()A.24B．64C．2 2 D.1 643．下列是y＝23x的图象的是()4．图中曲线是幂函数y ＝x n在第一象限的图象，已知n 取±2，±12四个值，则相应于曲线C 1，C 2，C 3，C 4的n依次为()A ．－2，－12，12，2B ．2，12，－12，－2C ．－12，－2,2，12D ．2，12，－2，－125．设a ＝2535，b ＝3525，c ＝2525，则a ，b ，c 的大小关系是()A ．a>c>bB ．a>b>cC ．c>a>bD ．b>c>a6．函数f(x)＝x α，x ∈(－1,0)∪(0,1)，若不等式f(x)>|x|成立，则在α∈{－2，－1,0,1,2}的条件下，α可以取值的个数是()A ．0B ．2C ．3D ．47．给出以下结论：①当α＝0时，函数y ＝x α的图象是一条直线；②幂函数的图象都经过(0,0)，(1,1)两点；③若幂函数y ＝x α的图象关于原点对称，则y ＝x α在定义域内y 随x 的增大而增大；④幂函数的图象不可能在第四象限，但可能在第二象限．则正确结论的序号为________．8．函数y ＝12x ＋x －1的定义域是____________．9．已知函数y ＝x－2m －3的图象过原点，则实数m 的取值范围是____________________．10．比较 1.121、121.4、131.1的大小，并说明理由．11．如图，幂函数y ＝x3m －7(m ∈N )的图象关于y 轴对称，且与x 轴、y 轴均无交点，求此函数的解析式．能力提升12．已知函数f(x)＝(m 2＋2m)·21mm x，m 为何值时，函数f(x)是：(1)正比例函数；(2)反比例函数；(3)二次函数；(4)幂函数．13．点(2，2)在幂函数f(x)的图象上，点(－2，14)在幂函数g(x)的图象上，问当x 为何值时，有：(1)f(x)>g(x)；(2)f(x)＝g(x)；(3)f(x)<g(x)．1．幂函数在第一象限内指数变化规律：在第一象限内直线x ＝1的右侧，图象从上到下，相应的指数由大变小；在直线x ＝1的左侧，图象从下到上，相应的指数由大变小．2．求幂函数的定义域时要看指数的正负和指数nm中的m 是否为偶数；判断幂函数的奇偶性时要看指数n m中的m 、n 是奇数还是偶数．y ＝x α，当α＝n m(m 、n ∈N *，m 、n 互质)时，有：n m y ＝nmx 的奇偶性定义域奇数偶数非奇非偶函数[0，＋∞) 偶数奇数偶函数(－∞，＋∞) 奇数奇数奇函数(－∞，＋∞) 3.幂函数y ＝nmx的单调性，在(0，＋∞)上，n m>0时为增函数，n m<0时为减函数．。

专题20 幂函数【知识点梳理】 知识点一：幂函数概念 形如()yx R αα=∈的函数，叫做幂函数，其中α为常数.知识点诠释： 幂函数必须是形如()yx R αα=∈的函数，幂函数底数为单一的自变量x ，系数为1，指数为常数.例如：()2423,1,2y x y x y x ==+=-等都不是幂函数.知识点二：幂函数的图象及性质 1.作出下列函数的图象：(1)x y =；(2)21x y =；(3)2x y =；(4)1-=x y ；(5)3x y =．知识点诠释：幂函数随着α的取值不同，它们的定义域、性质和图象也不尽相同，但它们有一些共同的性质： (1)所有的幂函数在(0，+∞)都有定义，并且图象都过点(1，1)；(2)0>α时，幂函数的图象通过原点，并且在区间),0[+∞上是增函数．特别地，当1>α时，幂函数的图象下凸；当10<<α时，幂函数的图象上凸；(3)0<α时，幂函数的图象在区间),0(+∞上是减函数．在第一象限内，当x 从右边趋向原点时，图象在y 轴右方无限地逼近y 轴正半轴，当x 趋于∞+时，图象在x 轴上方无限地逼近x 轴正半轴．2.作幂函数图象的步骤如下: (1)先作出第一象限内的图象；(2)若幂函数的定义域为(0)+∞，或[0)+∞，，作图已完成； 若在()0-∞，或(]0-∞，上也有意义，则应先判断函数的奇偶性 如果为偶函数，则根据y 轴对称作出第二象限的图象； 如果为奇函数，则根据原点对称作出第三象限的图象.3.幂函数解析式的确定(1)借助幂函数的定义，设幂函数或确定函数中相应量的值． (2)结合幂函数的性质，分析幂函数中指数的特征．(3)如函数()af x k x =⋅是幂函数，求()f x 的表达式，就应由定义知必有1k =，即()af x x =．4.幂函数值大小的比较(1)比较函数值的大小问题一般是利用函数的单调性，当不便于利用单调性时，可与0和1进行比较．常称为“搭桥”法．(2)比较幂函数值的大小，一般先构造幂函数并明确其单调性，然后由单调性判断值的大小． (3)常用的步骤是：①构造幂函数；②比较底的大小；③由单调性确定函数值的大小．【题型归纳目录】 题型一：幂函数的概念 题型二：幂函数的图象的应用 题型三：幂函数的单调性 题型四：幂函数的奇偶性 题型五：幂值大小的比较 题型六：定点问题 题型七：定义域问题 题型八：值域问题【典型例题】 题型一：幂函数的概念1．（2022·河北沧州·高一期末）下列函数是幂函数的是（ ） A ．2y x = B ．21y x =- C ．3y x = D ．2x y =2．（2022·吉林·梅河口市第五中学高一期末）下列函数是幂函数的是（ ） A ．22y x = B ．1y x -=- C ．31y x = D ．2x y =3．（2022·河南新乡·高一期末）已知幂函数()()2311mf x m x =-在()0,∞+上单调递减，则()4f =（ ）A ．2B ．16C ．12D ．1164．（2022·四川·什邡中学高一阶段练习）已知点4)在幂函数()y f x =的图象上，则(2)f =_______．5．（2022·甘肃·甘南藏族自治州合作第一中学高一期末）幂函数()y f x =的图象经过点(14,2)，则1()4f =____.6．（2022·新疆·乌市一中高一期末）已知幂函数()f x 的图象过点18,2⎛⎫⎪⎝⎭，则127f ⎛⎫= ⎪⎝⎭________7．（2022·广东·深圳科学高中高一期中）若幂函数()21my m m x =--为偶函数，则m = ________ .8．（2022·甘肃庆阳·高一期末）已知幂函数()f x 的图象过点13,3⎛⎫ ⎪⎝⎭，则此函数的解析式为______．9．（2022·湖北·宜昌市夷陵中学高一期中）已知幂函数()2()1mf x m m x =--的图象关于y 轴对称，则()f m =___________．10．（2022·宁夏·青铜峡市宁朔中学高二期中（文））已知幂函数()()a f x x a R =∈过点A （4，2），则f （14）=___________.11．（2022·湖南·高一课时练习）已知()m x 是幂函数，若()()9271m m =，求()25m 和()8m ．题型二：幂函数的图象的应用1．（2021·河北省博野中学高一开学考试）函数2,y x y x ==和1y x=的图象如图所示，有下列四个说法： ①如果21a a a>>，那么01a <<； ②如果21a a a>>，那么1a >； ③如果21a a a>>，那么10a -<<； ④如果21a a a>>时，那么1a <-. 其中正确的是（ ）.A ．①④B ．①C ．①②D ．①③④2．（2020·上海市晋元高级中学高一期中）已知幂函数()y f x =的图象经过点14,2P ⎛⎫⎪⎝⎭，则()y f x =的大致图象是（ ）A ．B ．C ．D ．3．（2022·四川凉山·高一期末）如图，①②③④对应四个幂函数的图像，其中①对应的幂函数是（ ）A ．3y x =B ．2y xC ．y x =D ．58y x =4．（2022·宁夏吴忠区青铜峡市教育局高一开学考试）已知幂函数()f x 的图象过点()9,3，则函数()f x 的图象是（ ）A ．B ．C ．D ．5．（2022·辽宁大连·高一期末）已知幂函数a y x =与b y x =的部分图像如图所示，直线2x m =，()01x m m =<<与a y x =，b y x =的图像分别交于A ，B ，C ，D 四点，且AB CD =，则a b m m +=（ ）A ．12B ．1CD ．26．（2021·福建·高三学业考试）函数y = ）A ．B ．C ．D ．7．（2021·全国·高一单元测试）图中C 1、C 2、C 3为三个幂函数y x α=在第一象限内的图象，则解析式中指数α的值依次可以是（ ）A ．12、3、1-B ．1-、3、12C ．12、1-、3D ．1-、12、38．（2021·全国·高一课时练习）若幂函数m y x =与n y x =在第一象限内的图像如图所示，则（ ）A ．101n m -<<<<；B ．1n <-，01m <<；C ．10n -<<，1m ；D ．1n <-，1m ．9．（2021·陕西·咸阳市实验中学高一阶段练习）若幂函数,a b y x y x ==在同一坐标系中的部分图象如图所示，则a ､b 的大小关系正确的是（ ）A ．1a b >>B ．1b a >>C ．0a b >>D ．0b a >>（多选题）10．（2021·全国·高一课时练习）下列关于幂函数y x α=的性质说法正确的有（ ） A ．当1α=-时，函数在其定义域上递减 B ．当0α=时，函数图象是一条直线 C ．当2α=时，函数是偶函数D ．当3α=时，函数的图象与x 轴交点的横坐标为0（多选题）11．（2022·广东·韶关市田家炳中学高一期末）如果幂函数()22233m m y m m x--=-+的图象不过原点，则实数m 的取值为（ ） A ．0 B ．2 C ．1 D ．无解12．（2022·湖南·高一课时练习）对幂函数y x α=，填空：（1）当1α>，0x ≥时，图象恒过______和______两点；其中当01x <<时，幂函数图象在y x =图象的______方；当1x >时，幂函数图象在y x =图象的______方．（2）当01α<<，0x ≥时，图象也恒过______和______两点；其中当01x <<时，幂函数图象在y x =图象的______方；当1x >，幂函数图象在y x =图象的______方． （3）当0α<，0x >时，图象恒过点______．题型三：幂函数的单调性1．（2022·四川成都·高一开学考试）下列幂函数中，既是奇函数又在区间()0,∞+单调递增的是（ ）A ．()3f x x =B ．()2f x x =C ．()12f x x =D ．()1f x x -=2．（2022·湖南·株洲二中高一阶段练习）已知函数()22my m m x =+幂函数，且在其定义域内为单调函数，则实数m =（ ） A ．12B ．1-C ．12或1-D ．12-3．（2022·四川凉山·高一期末）已知0a ≠，若()2021202120a b a a b ++++=，则ba=（ ） A ．－2 B ．－1C ．12-D ．2（多选题）4．（2022·安徽·泾县中学高一阶段练习）已知函数()a f x x 的图象经过点1,33⎛⎫⎪⎝⎭则（ ）A ．()f x 的图象经过点(3,9)B ．()f x 的图象关于y 轴对称C ．()f x 在(0,)+∞上单调递减D ．()f x 在(0,)+∞内的值域为(0,)+∞5．（2022·全国·池州市第一中学高一开学考试）已知幂函数()()213m f x m x -=-在()0,∞+内是单调递减函数，则实数m =______．6．（2022·北京房山·高一期末）试写出函数()f x ，使得()f x 同时()f x 满足以下条件： ①定义域为[)0,∞+；②值域为[)0,∞+；③在定义域内是单调增函数．则函数()f x 的解析式可以是_______（写出一个满足题目条件的解析式）．7．（2022·湖南·高一课时练习）已知2.4α>2.5α，则α的取值范围是________．8．（2022·湖南·高一课时练习）已知幂函数()f x x α=的图象经过点3,19⎛⎫ ⎪⎝⎭，求函数的解析式，并作出该函数图象的草图，判断该函数的奇偶性和单调性．9．（2022·湖南·高一课时练习）结合图中的五个函数图象回答问题：(1)哪几个是偶函数，哪几个是奇函数？ (2)写出每个函数的定义域、值域； (3)写出每个函数的单调区间； (4)从图中你发现了什么？10．（2022·湖南·高一课时练习）已知幂函数()f x x α=的图象经过点1(8,)2，求函数的解析式，并作出该函数图象的草图，判断该函数的奇偶性和单调性．11．（2022·全国·高一课时练习）求函数2()(2)f x x -=+的定义域，并指出其单调区间.题型四：幂函数的奇偶性1．（2022·北京丰台·高一期末）下列函数中，图象关于坐标原点对称的是（ ）A ．y =B ．3y x =C ．y x =D ．2x y =2．（2022·江西·景德镇一中高一期末）已知幂函数()y f x =的图象过，则下列结论正确的是（ ）A ．()y f x =的定义域为[0,)+∞B ．()y f x =在其定义域内为减函数C ．()y f x =是偶函数D ．()y f x =是奇函数3．（2022·四川雅安·高一期末）已知幂函数()()2133a f x a a x +=-+为偶函数，则实数a 的值为（ ）A ．3B ．2C ．1D ．1或2（多选题）4．（2022·安徽阜阳·高一期中）已知函数()21m my m x -=-为幂函数，则该函数为（ ）A ．奇函数B ．偶函数C ．区间()0,∞+上的增函数D ．区间()0,∞+上的减函数（多选题）5．（2022·广东深圳·高一期末）若函数()2()3104m f x m m x =-+是幂函数，则()f x 一定（ ）A ．是偶函数B ．是奇函数C ．在(,0)x ∈-∞上单调递减D ．在(,0)x ∈-∞上单调递增（多选题）6．（2022·广西钦州·高一期末）若函数()2231()69m m f x m m x-+=-+是幂函数且为奇函数，则m的值为（ ） A ．1 B ．2 C ．3 D ．47．（2022·湖南·湘潭一中高一期末）已知幂函数()()221m f x m m x +=-+是奇函数，则m =___________.8．（2022·湖南怀化·高一期末）写出一个同时具有下列三个性质的函数：()f x =________.①()()f x x R αα=∈；②()f x 在R 上单调递增；③()()f x f x -=-.9．（2022·河南南阳·高一期末）写出一个同时具有下列三个性质的函数：()f x =___________. ①()f x 为幂函数；②()f x 为偶函数；③()f x 在(),0∞-上单调递减.10．（2022·黑龙江绥化·高一期末）已知幂函数f (x )是奇函数且在(0,)+∞上是减函数，请写出f (x )的一个表达式________．11．（2022·山东·济南一中高一阶段练习）已知幂函数()223m m y xm N --*=∈的图象关于y 轴对称，且在()0,∞+上单调递减，则满足()()33132mma a --+<-的a 的取值范围为________.12．（2022·重庆巫山·高一期末）若幂函数()f x 过点()2,8，则满足不等式()()310f a f a -+-≤的实数a 的取值范围是______13．（2022·上海·同济大学第二附属中学高一期末）已知α∈112,1,,,1,2,322⎧⎫---⎨⎬⎩⎭.若幂函数f (x )＝xα为奇函数，且在(0，＋∞)上递减，则α＝______.14．（2022·北京房山·高一期末）已知幂函数()f x x α=的图象经过点2)． (1)求函数()f x 的解析式；(2)若函数()f x 满足条件(2)(1)f a f a ->- ，试求实数a 的取值范围．15．（2022·上海市第三女子中学高一期末）已知幂函数()()24Z m mf x x m -+=∈的图象关于y 轴对称，且在区间()0,+∞上是严格增函数． (1)求m 的值；(2)求满足不等式()()211f a f a -<+的实数a 的取值范围．16．（2022·全国·高一课时练习）判断函数3y x -=与2y x 的奇偶性.题型五：幂值大小的比较1．（2022·湖北·华中师大一附中高一期末）已知幂函数a y x =的图象过点13,9⎛⎫⎪⎝⎭，则下列两函数的大小关系为：()224ax x -+（ ）(3)a - A ．≤ B ．≥ C ．< D ．>2．（2021·山东聊城一中高一期中）设幂函数()f x 的图像经过点12⎛ ⎝，若实数1m ，则()f m 与()1f m -的大小关系是（ ）A ．()()1f m f m ->B ．()()1f m f m -<C ．()()1f m f m -=D ．以上都有可能3．（2021·江苏·高一专题练习）下列比较大小中正确的是（ ）. A ．0.50.532()()23<B ．1123()()35---<-C ．3377( 2.1)( 2.2)--<-D ．443311()()23-<4．（2022·湖南·高一课时练习）已知()()1230m a a -=+≠，13n -=，则m 与n 的大小关系为________．5．（2022·全国·高一）比较下列各组数的大小． （1）11331.5 1.71,,；（2）22433310(,,1.()17-－－；（3）2235353.()8 3.9 1.8-－，，；6．（2021·全国·高一课前预习）求出函数2245()44x x f x x x ++=++的单调区间，并比较()f π-与f ⎛ ⎝⎭的大小．7．（2021·全国·高一课时练习）已知幂函数()0,R my xm m =<∈.(1)求证：该函数在区间()0,∞+上是严格减函数； (2)利用（1）的结论，比较1ca ⎛⎫ ⎪⎝⎭与1cb ⎛⎫⎪⎝⎭()0,0a b c >>>的大小关系.8．（2021·江苏·高一课时练习）比较下列各组数中两个数的大小（0a >）： （1）560.31，560.35； （2）13-，13-； （3） 1.5(1)a +， 1.5a ； （4）23(2)a -+，232-.9．（2021·全国·高一课时练习）已知223()m m f x x +-=（m ∈Z ）的图像关于y 轴对称且在(0,)+∞上()f x 随着x 值的增大而减小，求()f x 的解析式及其定义域、值域，并比较(2)f -与(1)f -的大小.10．（2021·全国·高一课时练习）比较下列各组中两个数的大小，并说明理由． （1）120.75，120.76；（2）()30.95-，()30.96-．11．（2021·全国·高一专题练习）比较下列各组数的大小：（1）5-23和523.1-；（2）788--和781()9-；（3）232()3--和23()6π--；题型六：定点问题1．（2022·全国·高一）下列命题中正确的是（ ） A ．幂函数的图象一定过点（0，0）和点（1，1）B ．若函数f （x ）＝xn 是奇函数，则它在定义域上单调递增C ．幂函数的图象上的点一定不在第四象限D ．幂函数的图象不可能是直线2．（2022·全国·高三专题练习）下列结论正确的是（ ） A ．幂函数图象一定过原点B ．当0α<时，幂函数y x α=是减函数C ．当1α>时，幂函数y x α=是增函数D ．函数2y x 既是二次函数，也是幂函数3．（2021·全国·高一课时练习）下列命题中正确的是（ ） A ．当0α=时，函数y x α=的图像是一条直线； B ．幂函数的图像都经过()0,0和()1,1点； C ．幂函数32y x -=的定义域为[)0,∞+； D ．幂函数的图像不可能出现在第四象限．（多选题）4．（2022·福建漳州·高一期末）已知幕函数()f x x α=的图象经过点()4,2，则（ ）A ．函数()f x 是偶函数B ．函数()f x 是增函数C ．函数()f x 的图象一定经过点()0,1D ．函数()f x 的最小值为0（多选题）5．（2022·全国·高三专题练习）下列关于幂函数图象和性质的描述中，正确的是（ ） A ．幂函数的图象都过(1,1)点B ．幂函数的图象都不经过第四象限C ．幂函数必定是奇函数或偶函数中的一种D ．幂函数必定是增函数或减函数中的一种6．（2022·全国·高三专题练习）如图是幂函数i y x α=（αi ＞0，i ＝1，2，3，4，5）在第一象限内的图象，其中α1＝3，α2＝2，α3＝1，412α=，513α=，已知它们具有性质： ①都经过点（0，0）和（1，1）； ②在第一象限都是增函数．请你根据图象写出它们在（1，+∞）上的另外一个共同性质：___________．7．（2021·湖南·衡阳市田家炳实验中学高一期中）若幂函数()221()1m f x m m x -=--的图象经过点()0,0，则m =________．8．（2022·北京·高一期末）幂函数()y f x =的图象恒过点_________，若幂函数()y f x =的图象过点()2,4，则此函数的解析式是____________．9．（2022·湖南·高一课时练习）对幂函数y x α=，填空：（1）当1α>，0x ≥时，图象恒过______和______两点；其中当01x <<时，幂函数图象在y x =图象的______方；当1x >时，幂函数图象在y x =图象的______方．（2）当01α<<，0x ≥时，图象也恒过______和______两点；其中当01x <<时，幂函数图象在y x =图象的______方；当1x >，幂函数图象在y x =图象的______方． （3）当0α<，0x >时，图象恒过点______．题型七：定义域问题1．（2022·山西吕梁·高一期末）已知幂函数()f x 的图象过点(，则()f x 的定义域为（ ） A ．R B ．()0,∞+ C ．[)0,∞+ D ．()(),00,∞-+∞2．（2022·全国·高一课时练习）设α∈11,132⎧⎫-⎨⎬⎩⎭，，，则使函数y ＝xα的定义域为R 的所有α的值为（ ）A ．1,3B ．－1,1C ．－1,3D ．－1,1,33．（2022·黑龙江绥化·高一期末）函数4()(1)f x x =- ） A ．()1，∞+ B ．(2,)-+∞C ．()()211∞-⋃+，，D ．R4．（2021·河北·石家庄市藁城区第一中学高一阶段练习）已知幂函数()y f x =的图象过点⎛ ⎝⎭，则下列关于()f x 说法正确的是（ ） A ．奇函数B ．偶函数C ．在(0,)+∞单调递减D ．定义域为[0,)+∞5．（2021·陕西·西安市第三中学高一期中）幂函数a y x =中a 的取值集合C 是11,0,,1,2,32⎧⎫-⎨⎬⎩⎭的子集，当幂函数的值域与定义域相同时，集合C 为（ ） A ．11,0,2⎧⎫-⎨⎬⎩⎭B ．1,1,22⎧⎫⎨⎬⎩⎭C ．11,,32⎧⎫-⎨⎬⎩⎭D ．1,1,2,32⎧⎫⎨⎬⎩⎭（多选题）6．（2022·海南鑫源高级中学高一期末）若函数()f x x α=的定义域为R 且为奇函数，则α可能的值为（ ） A ．1- B ．1 C ．2 D ．37．（2022·内蒙古·赤峰红旗中学松山分校高一期末）已知幂函数()1*4n y x n N -=∈的定义域为()0,∞+，且单调递减，则n =________.8．（2022·辽宁丹东·高一期末）写出一个具有性质①②③的函数()f x =______． ①()f x 定义域为{}0x x ≠；②()f x 在(),0∞-单调递增；③()()()f ab f a f b =⋅．9．（2022·全国·高一课时练习）求函数2()(2)f x x -=+的定义域，并指出其单调区间.题型八：值域问题1．（2022·安徽·歙县教研室高一期末）已知幂函数()f x x α=的图象过点2⎫⎪⎪⎝⎭，则下列说法中正确的是（ ）A ．()f x 的定义域为RB ．()f x 的值域为[)0,∞+C ．()f x 为偶函数D ．()f x 为减函数2．（2022·广东·广州六中高一期末）幂函数()y f x =的图象过点(，则函数()y x f x =-的值域是（ ） A ．(),-∞+∞ B ．1,4⎛⎫-∞ ⎪⎝⎭C ．1,4⎡⎫-+∞⎪⎢⎣⎭D ．1,4⎛⎫-+∞ ⎪⎝⎭（多选题）3．（2022·江西省丰城中学高一开学考试）已知函数()f x x α=图像经过点(4,2)，则下列命题正确的有（ ） A ．函数为增函数 B ．函数为偶函数 C ．若1x >，则()1f x > D ．若120x x <<，则()()121222f x f x x x f ++⎛⎫< ⎪⎝⎭4．（2022·北京房山·高一期末）试写出函数()f x ，使得()f x 同时()f x 满足以下条件： ①定义域为[)0,∞+；②值域为[)0,∞+；③在定义域内是单调增函数．则函数()f x 的解析式可以是_______（写出一个满足题目条件的解析式）．5．（2021·江苏·高一专题练习）函数213324y x x =++，其中8x ，则其值域为___________.6．（2021·全国·高一课时练习）已知函数2(),x af x x x a=>⎪⎩，若函数()f x 的值域为R ，则实数a 的取值范围为__________．7．（2022·湖南·高一课时练习）已知幂函数()()226Z m m f x x m --=∈在区间()0,∞+上是减函数．(1)求函数()f x 的解析式；(2)讨论函数()f x 的奇偶性和单调性； (3)求函数()f x 的值域．8．（2022·全国·高一课时练习）写出函数53y x =与15y x =的定义域和值域.9．（2021·全国·高一课时练习）（1）使用五点作图法，在图中画出()23f x x =的图象，并注明定义域．（2）求函数()423323h x x x =--的值域．10．（2021·江苏·高一专题练习）已知幂函数()2()1()kf x k k x k R =--∈，且在区间(0,)+∞内函数图象是上升的．（1）求实数k 的值；（2）若存在实数a ，b 使得函数f （x ）在区间[a ，b ]上的值域为[a ，b ]，求实数a ，b 的值．11．（2019·全国·高一课时练习）已知幂函数()()22421m m f x m x -+=-在()0,∞+上单调递增.（1）求m 的值；（2）当[]1,2x ∈时，记()f x 的值域为集合A ，若集合[]2,4B k k =--，且A B A ⋃=，求实数k 的取值范围.。

第七节幂函数❖基础知识1．幂函数的概念一般地，形如y＝xα(α∈R)的函数称为幂函数，其中底数x是自变量，α为常数．幂函数的特征(1)自变量x处在幂底数的位置，幂指数α为常数；(2)xα的系数为1；(3)只有一项．2．五种常见幂函数的图象与性质函数特征性质y＝x y＝x2y＝x3y＝x12y＝x－1图象定义域R R R{x|x≥0}{x|x≠0} 值域R{y|y≥0}R{y|y≥0}{y|y≠0} 奇偶性奇偶奇非奇非偶奇单调性增(－∞，0)减，(0，＋∞)增增增(－∞，0)和(0，＋∞)减公共点(1,1) ❖常用结论对于形如f(x)＝x nm(其中m∈N*，n∈Z，m与n互质)的幂函数：(1)当n为偶数时，f(x)为偶函数，图象关于y轴对称；(2)当m，n都为奇数时，f(x)为奇函数，图象关于原点对称；(3)当m为偶数时，x>0(或x≥0)，f(x)是非奇非偶函数，图象只在第一象限(或第一象限及原点处)．考点一幂函数的图象与性质[典例](1)(2019·赣州阶段测试)幂函数y＝f(x)的图象经过点(3，33)，则f(x)是()A．偶函数，且在(0，＋∞)上是增函数B ．偶函数，且在(0，＋∞)上是减函数C ．奇函数，且在(0，＋∞)上是增函数D ．非奇非偶函数，且在(0，＋∞)上是减函数 (2)已知幂函数f (x )＝(n 2＋2n －2)x23－n n (n ∈Z)的图象关于y 轴对称，且在(0，＋∞)上是减函数，则n 的值为( )A ．－3B ．1C ．2D ．1或2[解析](1)设f (x )＝x α，将点(3，33)代入f (x )＝x α，解得α＝13，所以f (x )＝x 13，可知函数f (x )是奇函数，且在(0，＋∞)上是增函数，故选C. (2)∵幂函数f (x )＝(n 2＋2n －2)x23－n n在(0，＋∞)上是减函数，∴⎩⎪⎨⎪⎧n 2＋2n －2＝1，n 2－3n <0，∴n ＝1， 又n ＝1时，f (x )＝x －2的图象关于y 轴对称，故n ＝1.[答案] (1)C (2)B[解题技法] 幂函数y ＝x α的主要性质及解题策略(1)幂函数在(0，＋∞)内都有定义，幂函数的图象都过定点(1,1)．(2)当α>0时，幂函数的图象经过点(1,1)和(0,0)，且在(0，＋∞)内单调递增；当α<0时，幂函数的图象经过点(1,1)，且在(0，＋∞)内单调递减．(3)当α为奇数时，幂函数为奇函数；当α为偶数时，幂函数为偶函数．(4)幂函数的性质因幂指数大于零、等于零或小于零而不同，解题中要善于根据幂指数的符号和其他性质确定幂函数的解析式、参数取值等．[题组训练]1.[口诀第3、4、5句]下列函数中，既是偶函数，又在区间(0，＋∞)上单调递减的为( )A ．y ＝x －4 B ．y ＝x －1 C ．y ＝x 2D ．y ＝x 13解析：选A 函数y ＝x －4为偶函数，且在区间(0，＋∞)上单调递减；函数y ＝x －1为奇函数，且在区间(0，＋∞)上单调递减；函数y ＝x 2为偶函数，且在区间(0，＋∞)上单调递增；函数y ＝x 13为奇函数，且在区间(0，＋∞)上单调递增．2.[口诀第2、3、4句]已知当x ∈(0,1)时，函数y ＝x p 的图象在直线y ＝x 的上方，则p 的取值范围是________．解析：当p >0时，根据题意知p <1，所以0<p <1；当p ＝0时，函数为y ＝1(x ≠0)，符合题意；当p <0时，函数y ＝x p 的图象过点(1,1)，在(0，＋∞)上为减函数，符合题意．综上所述，p 的取值范围是(－∞，1)．答案：(－∞，1)考点二 比较幂值大小[典例] 若a ＝⎝⎛⎭⎫1223，b ＝⎝⎛⎭⎫1523，c ＝⎝⎛⎭⎫1213，则a ，b ，c 的大小关系是( ) A ．a <b <c B ．c <a <b C ．b <c <aD ．b <a <c[解析] 因为y ＝x 23在第一象限内是增函数，所以a ＝⎝⎛⎭⎫1223>b ＝⎝⎛⎭⎫1523，因为y ＝⎝⎛⎭⎫12x 是减函数，所以a ＝⎝⎛⎭⎫1223<c ＝⎝⎛⎭⎫1213，所以b <a <c . [答案] D[题组训练]1．若a ＝⎝⎛⎭⎫3525，b ＝⎝⎛⎭⎫2535，c ＝⎝⎛⎭⎫2525，则a ，b ，c 的大小关系是( ) A ．a >b >c B ．a >c >b C ．c >a >bD ．b >c >a解析：选B 因为y ＝x 25在第一象限内为增函数，所以a ＝⎝⎛⎭⎫3525>c ＝⎝⎛⎭⎫2525，因为y ＝⎝⎛⎭⎫25x 是减函数，所以c ＝⎝⎛⎭⎫2525>b ＝⎝⎛⎭⎫2535，所以a >c >b . 2．若(a ＋1)12<(3－2a )12，则实数a 的取值范围是________． 解析：易知函数y ＝x 12的定义域为[0，＋∞)，在定义域内为增函数，所以⎩⎪⎨⎪⎧a ＋1≥0，3－2a ≥0，a ＋1<3－2a ，解得－1≤a <23.答案：⎣⎡⎭⎫－1，23 [课时跟踪检测]1．若幂函数y ＝f (x )的图象过点(4,2)，则f (8)的值为( )A ．4 B. 2 C ．2 2D ．1解析：选C 设f (x )＝x n ，由条件知f (4)＝2，所以2＝4n ，n ＝12，所以f (x )＝x 12，f (8)＝812＝2 2.2．若幂函数f (x )＝x k 在(0，＋∞)上是减函数，则k 可能是( )A ．1B ．2 C.12D ．－1解析：选D 由幂函数的性质得k <0，故选D. 3．已知幂函数f (x )＝(m 2－3m ＋3)x m＋1为偶函数，则m ＝( ) A ．1 B ．2 C ．1或2D ．3解析：选A ∵函数f (x )为幂函数，∴m 2－3m ＋3＝1，即m 2－3m ＋2＝0，解得m ＝1或m ＝2.当m ＝1时，幂函数f (x )＝x 2为偶函数，满足条件；当m ＝2时，幂函数f (x )＝x 3为奇函数，不满足条件．故选A.4．(2018·邢台期末)已知幂函数f (x )的图象过点⎝⎛⎭⎫2，14，则函数g (x )＝f (x )＋x24的最小值为( ) A ．1 B ．2 C ．4D ．6解析：选A 设幂函数f (x )＝x α.∵f (x )的图象过点⎝⎛⎭⎫2，14，∴2α＝14，解得α＝－2. ∴函数f (x )＝x －2，其中x ≠0. ∴函数g (x )＝f (x )＋x 24＝x －2＋x 24＝1x 2＋x 24≥21x 2·x 24＝1， 当且仅当x ＝±2时，g (x )取得最小值1. 5．(2019·安徽名校联考)幂函数y ＝x |m －1|与y ＝x 23－m m (m ∈Z)在(0，＋∞)上都是增函数，则满足条件的整数m 的值为( )A ．0B ．1和2C ．2D ．0和3解析：选C 由题意可得⎩⎪⎨⎪⎧|m －1|>0，3m －m 2>0，m ∈Z ，解得m ＝2.6．已知a ＝345，b ＝425，c ＝1215，则a ，b ，c 的大小关系为( )A ．b <a <cB ．a <b <cC ．c <b <aD ．c <a <b解析：选C 因为a ＝8115，b ＝1615，c ＝1215，由幂函数y ＝x 15在(0，＋∞)上为增函数，知a >b >c ，故选C.7．设x ＝0.20.3，y ＝0.30.2，z ＝0.30.3，则x ，y ，z 的大小关系为( )A ．x <z <yB ．y <x <zC ．y <z <xD ．z <y <x解析：选A 由函数y ＝0.3x 在R 上单调递减，可得y >z .由函数y ＝x 0.3在(0，＋∞)上单调递增，可得x <z .所以x <z <y .8．已知幂函数f (x )＝(m －1)2x242－＋m m 在(0，＋∞)上单调递增，函数g (x )＝2x －k ，当x ∈[1,2)时，记f (x )，g (x )的值域分别为集合A ，B ，若A ∪B ＝A ，则实数k 的取值范围是( )A ．(0,1)B ．[0,1)C ．(0,1]D ．[0,1]解析：选D ∵f (x )是幂函数，∴(m －1)2＝1，解得m ＝2或m ＝0.若m ＝2，则f (x )＝x －2在(0，＋∞)上单调递减，不满足条件．若m ＝0，则f (x )＝x 2在(0，＋∞)上单调递增，满足条件，即f (x )＝x 2.当x ∈[1,2)时，f (x )∈[1,4)，即A ＝[1,4)；当x ∈[1,2)时，g (x )∈[2－k,4－k )，即B ＝[2－k,4－k )．∵A ∪B ＝A ，∴B ⊆A ，∴2－k ≥1且4－k ≤4，解得0≤k ≤1.9．若f (x )是幂函数，且满足f (9)f (3)＝2，则f ⎝⎛⎭⎫19＝________. 解析：设f (x )＝x α，∵f (9)f (3)＝9α3α＝3α＝2，∴f ⎝⎛⎭⎫19＝⎝⎛⎭⎫19α＝⎝⎛⎭⎫132α＝132α＝122＝14. 答案：1410．已知函数f (x )＝(m 2－m －5)x m 是幂函数，且在(0，＋∞)上为增函数，则实数m 的值是________． 解析：由f (x )＝(m 2－m －5)x m 是幂函数⇒m 2－m －5＝1⇒m ＝－2或m ＝3.又f (x )在(0，＋∞)上是增函数，所以m ＝3. 答案：311．当0＜x ＜1时，f (x )＝x 2，g (x )＝x 12，h (x )＝x －2，则f (x )，g (x )，h (x )的大小关系是________________． 解析：分别作出y ＝f (x )，y ＝g (x )，y ＝h (x )的图象如图所示，可知h (x )＞g (x )＞f (x )．答案：h (x )＞g (x )＞f (x )12．(2019·银川模拟)已知幂函数f (x )＝x12-，若f (a ＋1)<f (10－2a )，则a 的取值范围是________．解析：由题意得，幂函数f (x )＝x －12的定义域为(0，＋∞)，且函数f (x )在(0，＋∞)上单调递减，由f (a＋1)<f (10－2a )，得⎩⎪⎨⎪⎧a ＋1>10－2a ，a ＋1>0，10－2a >0，解得3<a <5.答案：(3,5)13．已知幂函数f (x )＝x()21－＋m m (m ∈N *)的图象经过点(2，2)．(1)试确定m 的值；(2)求满足条件f (2－a )>f (a －1)的实数a 的取值范围． 解：(1)∵幂函数f (x )的图象经过点(2，2)，∴2＝2()21－＋m m ，即212＝2()21－＋m m .∴m 2＋m ＝2，解得m ＝1或m ＝－2. 又∵m ∈N *，∴m ＝1. (2)由(1)知f (x )＝x 12，则函数的定义域为[0，＋∞)，并且在定义域上为增函数． 由f (2－a )>f (a －1)，得⎩⎪⎨⎪⎧2－a ≥0，a －1≥0，2－a >a －1，解得1≤a <32.∴a 的取值范围为⎣⎡⎭⎫1，32.。

幂的运算及幂函数1.几个公式 (1)α-a=αa 1 (2)m n nma a =(互质n m N n m a ,,,,0∈>) (3) mnnm aa1=-(互质n m N n m a ,,,,0∈>)2.运算法则________=*n m a a ________=÷n m a a ________)(=n m a ________)(=m ab ________)(=m ba当n 为奇数时,a a n n=,当n 为偶数时{0,0,||≥<-==a a a a n na a3、幂函数的定义4、幂函数的图像及性质掌握31,3,2,1,21,31,21,3,2-=-=-=-=-=====n n n n n n n n n 的图象 0>n 时，在+∞,0[）上递增，图象过（0，0）、（1，1） 0<n 时，在+∞,0[）上递减，图象过（1，1）幂函数为偶函数图象在一、二象限幂函数为奇函数图象在一、三象限幂函数为非奇非偶函数，图象只在第一象限 二、基础练习1．下列函数中是幂函数的是（ ）A xx y = B 2131x y = C x y )31(= D 3x y =2．下列函数定义域为非负实数集的是（ ） A 513-=xy B 21-=xy C 43x y = D 72x y =3．函数35y x =是 A ．奇函数B ．偶函数 C ．非奇非偶函数 D ．既是奇函数又是偶函数 4．函数32y x-=的定义域是 ，值域是 .5．比较下列各组值的大小.（1） 1.23， 1.24 （2）0.41()3-，0.41()4- 6. ____________2733443= 2._________)7(33=-__________)5(44=- 4_________)21(1212=- 三、典型例题例1、化简(1) 215.13241)6449()91(270001.0---+-+ (2))(1124--∙∙xy xy xy xy(3)833)(4160625.0304---π （4）)41()3()2(324132213141-----÷-∙b a b a b a练习1：计算（1）31021)6427(.)5(lg )972(-++ （2）、（8）32-2932)10(⨯÷510（3）332baab ba例2（1）、、已知nx y =的图象如图，则n=___________A 31-B 31C 32- D 32（2）31-=xy 的图象是（ ）练习1有3个幂函数的图象如图，则c b a ,,的大小关系为__________2幂函数322--=m m x y ，Z m ∈的图象如图，则m=________3122)2()(-++=m mx m m x f ,当m=______时，)(x f 为正比例函数，当m=_______时)(x f 为反比例函数。

幂函数一、幂函数的概念一般地，形如)(R x x y ∈=α的函数称为幂函数，其中x 是自变量，α是常数幂函数)(R x x y ∈=α 的图像在第一象限的分布规律：1当0>α时，幂函数y x α=有下列性质：（1）图象都通过点)1,1(),0,0(； （2）在第一象限内都是增函数；（3）在第一象限内1>α时，图象是向下凸的；10<<α时，图象是向上凸的； （4）在第一象限内，过点)1,1(后，α越大，图象上升的速度越快。

2当0<α时，幂函数y x α=有下列性质：（1）图象都通过点)1,1(；（2）在第一象限内都是减函数，图象是向下凸的；（3）在第一象限内，图象向上与y 轴无限地接近；向右无限地与x 轴无限地接近； （4）在第一象限内，过点)1,1(后，α越大，图象下落的速度越快。

无论α取任何实数，幂函数y xα=的图象必然经过第一象限，并且一定不经过第四象限。

【典型例题】例1（定义） 已知221(22)23m y m m x n -=+-+-是幂函数，求m ，n 的值.例2（图像）写出下列函数的定义域，并画出函数图象、指出函数的单调性和奇偶性：12133243252(1)(2)(3)(4)(5)(6)y xy xy x y x y xy x ---= = = = ==例3（性质） 比例下列各组数的大小. （1）8787)91(8---和； （2）(–2)–3和(–2.5)–3；（3）533252)9.1()8.3(,)1.4(--和. （4）（－22）32-，（－710）32，1.134-；例4.已知幂函数（1） 若f(x)为偶函数，且在 上是增函数，求f(x)的解析式（2） 若在 上是减函数，求k 的取值范围例5.已知幂函数 的图象关于y 轴对称,且在 上是减函数，()*-∈=N m x y m 93()+∞,0()()m m a a a ---<+231的不等式解关于()()22231mm a a a -<+-的不等式【变式】解关于()()33231m ma a a -<+-的不等式【变式】解关于()+∞,0()+∞,0)(22123Z k x y k k ∈=-+幂函数作业：1.下列函数中，是幂函数的是（ ）A.y =－x 21B.y =3x 2C.y =x1D.y =2x2．下列四个命题中正确的有 A.幂函数的图象一定过（0，0）和（1，1） B.当α＜0时，幂函数y =x α是减函数 C.当α＞0时，幂函数y =x α是增函数 D.函数y =x 2既是二次函数，也是幂函数 E ．幂函数的图象不可能出现在第四象限内 F.当n=0时，幂函数n y x =图象是一条直线 3.函数y =x 53的图象大致是 ( )4．幂函数的图象过点(2,41), 则它的单调递增区间是。

幂函数（1）幂函数的定义： 一般地，函数y x α=叫做幂函数，其中x 为自变量，α是常数．（2）幂函数的图象①图象分布：幂函数图象分布在第一、二、三象限，第四象限无图象．幂函数是偶函数时，图象分布在第一、二象限(图象关于y 轴对称)；是奇函数时，图象分布在第一、三象限(图象关于原点对称)；是非奇非偶函数时，图象只分布在第一象限． ②过定点：所有的幂函数在(0,)+∞都有定义，并且图象都通过点(1,1)．③单调性：如果0α>，则幂函数的图象过原点，并且在[0,)+∞上为增函数．如果0α<，则幂函数的图象在(0,)+∞上为减函数，在第一象限内，图象无限接近x 轴与y 轴． ④奇偶性：当α为奇数时，幂函数为奇函数，当α为偶数时，幂函数为偶函数．当q pα=（其中,p q 互质，p 和q Z ∈），若p 为奇数q 为奇数时，则qpy x =是奇函数，若p 为奇数q 为偶数时，则qpy x =是偶函数，若p 为偶数q 为奇数时，则q py x =是非奇非偶函数． ⑤图象特征：幂函数,(0,)y x x α=∈+∞，当1α>时，若01x <<，其图象在直线y x =下方，若1x >，其图象在直线y x =上方，当1α<时，若01x <<，其图象在直线y x =上方，若1x >，其图象在直线y x =下方．幂函数练习题一、选择题：1．下列函数中既是偶函数又是(,)-∞0上是增函数的是 （ ）A ．y x =43B ．y x =32C ．y x =-2D ．y x =-142．函数2-=x y 在区间]2,21[上的最大值是（ ）A ．41B ．1-C ．4D ．4- 3．下列所给出的函数中，是幂函数的是（ ）A ．3x y -=B ．3-=xy C ．32x y = D ．13-=x y 4．函数34x y =的图象是（ ）A ．B ．C ．D ． 5．下列命题中准确的是 （ ） A ．当0=α时函数αx y =的图象是一条直线 B ．幂函数的图象都经过（0，0）和（1，1）点C ．若幂函数αx y =是奇函数，则αx y =是定义域上的增函数 D ．幂函数的图象不可能出现在第四象限 6．函数3x y =和31x y =图象满足（ ）A ．关于原点对称B ．关于x 轴对称C ．关于y 轴对称D ．关于直线x y =对称 7． 函数R x x x y ∈=|,|，满足（ ）A ．是奇函数又是减函数B ．是偶函数又是增函数C ．是奇函数又是增函数D ．是偶函数又是减函数8．如图1—9所示，幂函数αx y =在第一象限的图象，比较1,,,,,04321αααα的大小（ ）A ．102431<<<<<ααααB ．104321<<<<<ααααC ．134210αααα<<<<<D ．142310αααα<<<<<1α3α4α2α二、填空题：. 1．函数y x =-32的定义域是 .2．1()()f x f x -幂函数的图象过点（，则的解析式是.3．942--=a ax y 是偶函数，且在),0(+∞是减函数，则整数a 的值是 .4．函数2422-+=x x y 的单调递减区间是 .三、解答题：解答应写出文字说明．证明过程或演算步骤 1．比较下列各组中两个值大小 （1）060720880896116115353..(.)(.).与；（）与--2．求证：幂函数3x y =在R 上为奇函数且为增函数.3．下面六个幂函数的图象如图所示，试建立函数与图象之间的对应关系..6543212132323123---======x y x y x y x y x y x y ）；（）；（）（；）；（）；（）（（A ） （B ） （C ） （D ） （E ） （F ）巩固训练 一、选择题1．已知集合{}{}2,2,1==N M ，则N M 等于（ ） A ．{}2,1 B ．{}1 C ．{}2 D ．22．下列函数中，值域是()+∞,0的函数是（ ） A ．3x y = B ．4x y = C ．2-=x y D ．31-=xy3．函数11-=x y 的定义域是（ ） A ．()+∞,1 B ．[)+∞,1 C ．()1,∞- D ． ()()+∞∞-,11, 4．二次函数12+-=x y 的单调递减区间是（ ）A ．(]0,∞-B ．[)+∞,1C ．(]1,-∞-D ．[)+∞,0 5．函数3)(x x f -=的图象（ ）A ．关于直线x y =对称B ．关于x 轴对称C ．关于原点对称D ．关于y 轴对称 6．幂函数)(Q n x y n∈=的图象一定经过点（ ）A ．()0,0B ．()1,1C ．()1,1--D ．()1,0 7．已知{}512,>-==x x A R I ，则A =（ ）A ．{}3≤x xB ．{}2-≥x xC ．{}32≤≤-xD ．{}32≤≤-x x 8．若一元二次不等式0122<--px x 的解集是{}q x x <<-2，则p 的值是（ ） A ．不能确定 B ．4 C ．－4 D ．８ 10．函数)1(1≥--=x x y 的反函数是（ ） A ．)(12R x x y ∈+= B ．)0(12>+=x x y C ．)0(12≤+=x x y D ．)0(12≤+-=x x y11．已知)(x f 是定义在R 上的偶函数，且在[)+∞,0上单调递减，则（ ） A ．)10()()3(f f f <-<-π B ．)3()()10(-<-<f f f π C ．)10()3()(f f f <-<-π D ．)()3()10(π-<-<f f f 12．已知点()1,2+-b b a 与()b a 2,2+-关于直线x y =对称，则这两点之间的距离是（ ）A ．不能确定B ．314C ．213D ．21713．若不等式012<--kx kx 的解集是R ，则k 的取值范围是（ ） A ．04<<-k B ．04≤<-k C ．4-<k 或0>k D ．4-<k 或0≥k 14．已知)(x f 是奇函数，当0>x 时，其解析式1)(3++=x x x f ，则当0<x 时，)(x f 的解析式是（ ）A ．13-+x x B ．13---x x C ．13+-x x D ．13+--x x 二、填空题15．设函数)(x f 的定义域是{}10≤≤x x ，则)12(-x f 的定义域是___________ 18．已知幂函数)(x f 的图象经过()2,2 ，则)9(f =___________19．已知函数m x x f a+=)(的图象经过点()3,1 ，又其反函数图象经过点()2,10，则)(x f 的解析式为___________20．已知奇函数)(x f 在区间[]5,2上是减函数，且最小值为5-，则)(x f 在区间[]2,5--上的最大值是___________ 21．满足条件{}{}3,2,12,1⊆⊆M 的集合M的个数是___________个.22．函数x y --=11的反函数的值域是___________ 三、解答题23．已知{}⎭⎬⎫⎩⎨⎧>-=≤--=2,0822m m x x B x x x A ，若φ=B A ，求m 的取值范围。

幂函数考点和题型归纳一、基础知识1．幂函数的概念一般地，形如y＝xα(α∈R)的函数称为幂函数，其中底数x是自变量，α为常数．幂函数的特征(1)自变量x处在幂底数的位置，幂指数α为常数；(2)xα的系数为1；(3)只有一项．2．五种常见幂函数的图象与性质函数特征性质y＝x y＝x2y＝x3y＝x12y＝x－1图象定义域R R R{x|x≥0}{x|x≠0}值域R{y|y≥0}R{y|y≥0}{y|y≠0}奇偶性奇偶奇非奇非偶奇单调性增(－∞，0)减，(0，＋∞)增增增(－∞，0)和(0，＋∞)减公共点(1,1)二、常用结论对于形如f(x)＝x nm(其中m∈N*，n∈Z，m与n互质)的幂函数：(1)当n为偶数时，f(x)为偶函数，图象关于y轴对称；(2)当m，n都为奇数时，f(x)为奇函数，图象关于原点对称；(3)当m为偶数时，x>0(或x≥0)，f(x)是非奇非偶函数，图象只在第一象限(或第一象限及原点处)．考点一 幂函数的图象与性质[典例] (1)(2019·赣州阶段测试)幂函数y ＝f (x )的图象经过点(3，33)，则f (x )是( ) A ．偶函数，且在(0，＋∞)上是增函数 B ．偶函数，且在(0，＋∞)上是减函数 C ．奇函数，且在(0，＋∞)上是增函数 D ．非奇非偶函数，且在(0，＋∞)上是减函数 (2)已知幂函数f (x )＝(n 2＋2n －2)x 23－n n(n ∈Z)的图象关于y 轴对称，且在(0，＋∞)上是减函数，则n 的值为( )A ．－3B ．1C ．2D ．1或2[解析] (1)设f (x )＝x α，将点(3，33)代入f (x )＝x α，解得α＝13，所以f (x )＝x 13，可知函数f (x )是奇函数，且在(0，＋∞)上是增函数，故选C.(2)∵幂函数f (x )＝(n 2＋2n －2)x23－n n在(0，＋∞)上是减函数，∴⎩⎪⎨⎪⎧n 2＋2n －2＝1，n 2－3n <0，∴n ＝1，又n ＝1时，f (x )＝x －2的图象关于y 轴对称，故n ＝1. [答案] (1)C (2)B[解题技法] 幂函数y ＝x α的主要性质及解题策略(1)幂函数在(0，＋∞)内都有定义，幂函数的图象都过定点(1,1)．(2)当α>0时，幂函数的图象经过点(1,1)和(0,0)，且在(0，＋∞)内单调递增；当α<0时，幂函数的图象经过点(1,1)，且在(0，＋∞)内单调递减．(3)当α为奇数时，幂函数为奇函数；当α为偶数时，幂函数为偶函数．(4)幂函数的性质因幂指数大于零、等于零或小于零而不同，解题中要善于根据幂指数的符号和其他性质确定幂函数的解析式、参数取值等．[题组训练]1.[口诀第3、4、5句]下列函数中，既是偶函数，又在区间(0，＋∞)上单调递减的为( ) A ．y ＝x －4 B ．y ＝x －1 C ．y ＝x 2D ．y ＝x 13解析：选A 函数y ＝x －4为偶函数，且在区间(0，＋∞)上单调递减；函数y ＝x －1为奇函数，且在区间(0，＋∞)上单调递减；函数y ＝x 2为偶函数，且在区间(0，＋∞)上单调递增；函数y ＝x 13为奇函数，且在区间(0，＋∞)上单调递增．2.[口诀第2、3、4句]已知当x ∈(0,1)时，函数y ＝x p 的图象在直线y ＝x 的上方，则p 的取值范围是________．解析：当p >0时，根据题意知p <1，所以0<p <1；当p ＝0时，函数为y ＝1(x ≠0)，符合题意；当p <0时，函数y ＝x p 的图象过点(1,1)，在(0，＋∞)上为减函数，符合题意．综上所述，p 的取值范围是(－∞，1)．答案：(－∞，1)考点二 比较幂值大小[典例] 若a ＝⎝⎛⎭⎫1223，b ＝⎝⎛⎭⎫1523，c ＝⎝⎛⎭⎫1213，则a ，b ，c 的大小关系是( ) A ．a <b <c B ．c <a <b C ．b <c <aD ．b <a <c[解析] 因为y ＝x 23在第一象限内是增函数，所以a ＝⎝⎛⎭⎫1223>b ＝⎝⎛⎭⎫1523，因为y ＝⎝⎛⎭⎫12x 是减函数，所以a ＝⎝⎛⎭⎫1223<c ＝⎝⎛⎭⎫1213，所以b <a <c . [答案] D[题组训练]1．若a ＝⎝⎛⎭⎫3525，b ＝⎝⎛⎭⎫2535，c ＝⎝⎛⎭⎫2525，则a ，b ，c 的大小关系是( ) A ．a >b >c B ．a >c >b C ．c >a >bD ．b >c >a解析：选B 因为y ＝x 25在第一象限内为增函数，所以a ＝⎝⎛⎭⎫3525>c ＝⎝⎛⎭⎫2525，因为y ＝⎝⎛⎭⎫25x是减函数，所以c ＝⎝⎛⎭⎫2525>b ＝⎝⎛⎭⎫2535，所以a >c >b .2．若(a ＋1)12<(3－2a )12，则实数a 的取值范围是________． 解析：易知函数y ＝x 12的定义域为[0，＋∞)，在定义域内为增函数， 所以⎩⎪⎨⎪⎧a ＋1≥0，3－2a ≥0，a ＋1<3－2a ，解得－1≤a <23.答案：⎣⎡⎭⎫－1，23 [课时跟踪检测]1．若幂函数y ＝f (x )的图象过点(4,2)，则f (8)的值为( ) A ．4 B.2 C ．22D ．1解析：选C 设f (x )＝x n ，由条件知f (4)＝2，所以2＝4n ，n ＝12，所以f (x )＝x 12，f (8)＝812＝2 2.2．若幂函数f (x )＝x k 在(0，＋∞)上是减函数，则k 可能是( ) A ．1 B ．2 C.12D ．－1解析：选D 由幂函数的性质得k <0，故选D. 3．已知幂函数f (x )＝(m 2－3m ＋3)x m ＋1为偶函数，则m ＝( )A ．1B ．2C ．1或2D ．3解析：选A ∵函数f (x )为幂函数，∴m 2－3m ＋3＝1，即m 2－3m ＋2＝0，解得m ＝1或m ＝2.当m ＝1时，幂函数f (x )＝x 2为偶函数，满足条件；当m ＝2时，幂函数f (x )＝x 3为奇函数，不满足条件．故选A.4．(2018·邢台期末)已知幂函数f (x )的图象过点⎝⎛⎭⎫2，14，则函数g (x )＝f (x )＋x 24的最小值为( )A ．1B ．2C ．4D ．6解析：选A 设幂函数f (x )＝x α.∵f (x )的图象过点⎝⎛⎭⎫2，14，∴2α＝14，解得α＝－2. ∴函数f (x )＝x －2，其中x ≠0. ∴函数g (x )＝f (x )＋x 24＝x －2＋x 24＝1x 2＋x 24≥21x 2·x 24＝1， 当且仅当x ＝±2时，g (x )取得最小值1. 5．(2019·安徽名校联考)幂函数y ＝x |m －1|与y ＝x 23－m m (m ∈Z)在(0，＋∞)上都是增函数，则满足条件的整数m 的值为( )A ．0B ．1和2C ．2D ．0和3解析：选C由题意可得⎩⎪⎨⎪⎧|m －1|>0，3m －m 2>0，m ∈Z ，解得m ＝2.6．已知a ＝345，b ＝425，c ＝1215，则a ，b ，c 的大小关系为( ) A ．b <a <c B ．a <b <c C ．c <b <aD ．c <a <b解析：选C 因为a ＝8115，b ＝1615，c ＝1215，由幂函数y ＝x 15在(0，＋∞)上为增函数，知a >b >c ，故选C.7．设x ＝0.20.3，y ＝0.30.2，z ＝0.30.3，则x ，y ，z 的大小关系为( ) A ．x <z <y B ．y <x <z C ．y <z <xD ．z <y <x解析：选A 由函数y ＝0.3x 在R 上单调递减，可得y >z .由函数y ＝x 0.3在(0，＋∞)上单调递增，可得x <z .所以x <z <y .8．已知幂函数f (x )＝(m －1)2x242－＋m m 在(0，＋∞)上单调递增，函数g (x )＝2x －k ，当x∈[1,2)时，记f (x )，g (x )的值域分别为集合A ，B ，若A ∪B ＝A ，则实数k 的取值范围是( )A ．(0,1)B ．[0,1)C ．(0,1]D ．[0,1]解析：选D ∵f (x )是幂函数，∴(m －1)2＝1，解得m ＝2或m ＝0.若m ＝2，则f (x )＝x －2在(0，＋∞)上单调递减，不满足条件．若m ＝0，则f (x )＝x 2在(0，＋∞)上单调递增，满足条件，即f (x )＝x 2.当x ∈[1,2)时，f (x )∈[1,4)，即A ＝[1,4)；当x ∈[1,2)时，g (x )∈[2－k,4－k )，即B ＝[2－k,4－k )．∵A ∪B ＝A ，∴B ⊆A ，∴2－k ≥1且4－k ≤4，解得0≤k ≤1.9．若f (x )是幂函数，且满足f (9)f (3)＝2，则f ⎝⎛⎭⎫19＝________. 解析：设f (x )＝x α，∵f (9)f (3)＝9α3α＝3α＝2，∴f ⎝⎛⎭⎫19＝⎝⎛⎭⎫19α＝⎝⎛⎭⎫132α＝132α＝122＝14. 答案：1410．已知函数f (x )＝(m 2－m －5)x m 是幂函数，且在(0，＋∞)上为增函数，则实数m 的值是________．解析：由f (x )＝(m 2－m －5)x m 是幂函数⇒m 2－m －5＝1⇒m ＝－2或m ＝3.又f (x )在(0，＋∞)上是增函数，所以m ＝3.答案：311．当0＜x ＜1时，f (x )＝x 2，g (x )＝x 12，h (x )＝x －2，则f (x )，g (x )，h (x )的大小关系是________________．解析：分别作出y ＝f (x )，y ＝g (x )，y ＝h (x )的图象如图所示，可知h (x )＞g (x )＞f (x )．答案：h (x )＞g (x )＞f (x )12．(2019·银川模拟)已知幂函数f (x )＝x 12-，若f (a ＋1)<f (10－2a )，则a 的取值范围是________．解析：由题意得，幂函数f (x )＝x －12的定义域为(0，＋∞)，且函数f (x )在(0，＋∞)上单调递减，由f (a ＋1)<f (10－2a )，得⎩⎪⎨⎪⎧a ＋1>10－2a ，a ＋1>0，10－2a >0，解得3<a <5.答案：(3,5)13．已知幂函数f (x )＝x ()21－＋m m (m ∈N *)的图象经过点(2，2)．(1)试确定m 的值；(2)求满足条件f (2－a )>f (a －1)的实数a 的取值范围． 解：(1)∵幂函数f (x )的图象经过点(2，2)， ∴2＝2()21－＋m m ，即212＝2()21－＋m m .∴m 2＋m ＝2，解得m ＝1或m ＝－2. 又∵m ∈N *，∴m ＝1. (2)由(1)知f (x )＝x 12，则函数的定义域为[0，＋∞)，并且在定义域上为增函数． 由f (2－a )>f (a －1)，得⎩⎪⎨⎪⎧2－a ≥0，a －1≥0，2－a >a －1，解得1≤a <32.∴a 的取值范围为⎣⎡⎭⎫1，32.。

幂函数一、知识点总结1．幂函数的概念（1）一般地，幂函数的表达式为)(R ∈=ααx y ，其中α为常数；其特征是以幂的底为自变量，指数为常数。

（2）所有的幂函数在区间),0(+∞都有定义，并且图象都通过点(1,1)。

（3）学习和理解幂函数的概念时要注意以下几点：①形如 ,2,2,)2(+=∙==αααx y x y x y 形式的函数不是幂函数。

②幂函数αx y =中的α为任意实数。

③确定一个幂函数，只需求出α即可。

2．幂函数的图象我们只讨论幂函数αx y =中1,21,3,2,1-=α时的图象。

在同一平面直角坐标系作出幂函数12132,,,,-=====x y x y x y x y x y 的图象。

（1）列表、（2）描点：3）连线：用光滑的曲线将各点连结起来。

如图 （2）记熟上面各函数图象的形状，及它们之间的“高低”关系。

（3）函数xy 1=可记为1-=x y 。

（4）0>a 时，图象都过)1,1)(0,0(点，0<a 时，只过(1,1)不过(0,0)点。

3．幂函数的性质从上图可以观察到幂函数的特征如下：结合以上特征得幂函数的性质如下：（1）所有的幂函数在),0(+∞都有定义，并且图象都通过点(1,1)；（2）如果0>α，则幂函数的图象过原点，并且在区间),0[+∞上为增函数； （3）如果0<α，则幂函数的图象在区间),0(+∞上是减函数，在第一象限内，当x 从右边趋向于原点时，图象在y 轴右方无限地逼近y 轴，当x 趋向于∞+时，图象在x 轴上方无限地逼近x 轴；（4）当α为奇数时，幂函数为奇函数，当α为偶函数，幂函数为偶函数。

4．求幂函数的定义域、值域幂函数的定义域要根据解析式来确定，要保证解析式有意义，值域要在定义域范围内求解。

5．幂函数的单调性和奇偶性幂函数的单调性与奇偶性与一般函数的单调性和奇偶性相同，在证明或判断时，主要应用定义法判断，有时也用幂函数的性质加以判断。