三角函数竞赛讲义
- 格式:pdf
- 大小:536.72 KB
- 文档页数:4

第六章 三角函数一、基础知识定义1 角,一条射线绕着它的端点旋转得到的图形叫做角。
若旋转方向为逆时针方向,则角为正角,若旋转方向为顺时针方向,则角为负角,若不旋转则为零角。
角的大小是任意的。
定义2 角度制,把一周角360等分,每一等价为一度,弧度制:把等于半径长的圆弧所对的圆心角叫做一弧度。
360度=2π弧度。
若圆心角的弧长为L ,则其弧度数的绝对值|α|=rL ,其中r 是圆的半径。
定义3 三角函数,在直角坐标平面内,把角α的顶点放在原点,始边与x 轴的正半轴重合,在角的终边上任意取一个不同于原点的点P ,设它的坐标为(x ,y ),到原点的距离为r,则正弦函数s in α=r y ,余弦函数co s α=rx,正切函数tan α=x y ,余切函数cot α=y x ,正割函数se cα=xr,余割函数c s c α=.y r定理1 同角三角函数的基本关系式,倒数关系:tan α=αcot 1,s in α=αcsc 1,co s α=αsec 1;商数关系:tan α=αααααsin cos cot ,cos sin =;乘积关系:tan α×co s α=s in α,cot α×s in α=co s α;平方关系:s in 2α+co s 2α=1, tan 2α+1=se c 2α, cot 2α+1=c s c 2α.定理2 诱导公式(Ⅰ)s in (α+π)=-s in α, co s(π+α)=-co s α, tan (π+α)=tan α, cot (π+α)=cot α;(Ⅱ)s in (-α)=-s in α, co s(-α)=co s α, tan (-α)=-tan α, cot (-α)=cot α; (Ⅲ)s in (π-α)=s in α, co s(π-α)=-co s α, tan =(π-α)=-tan α, cot (π-α)=-cot α; (Ⅳ)s in ⎪⎭⎫⎝⎛-απ2=co s α, co s ⎪⎭⎫ ⎝⎛-απ2=s in α, tan ⎪⎭⎫⎝⎛-απ2=cot α(奇变偶不变,符号看象限)。
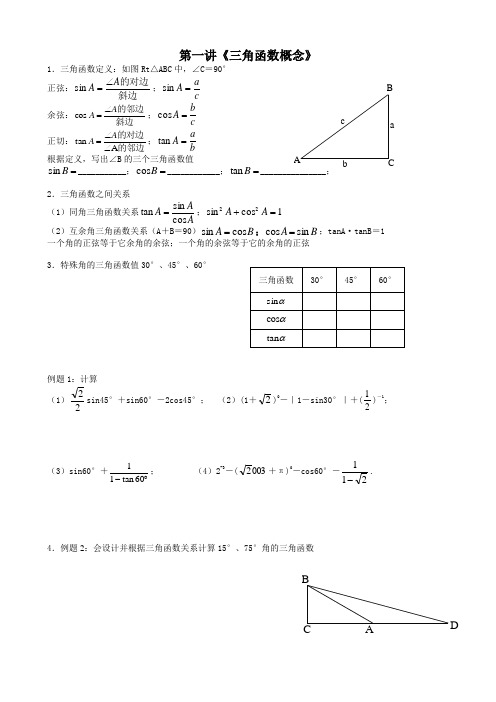
c ab B C A DC B A 第一讲《三角函数概念》1.三角函数定义:如图Rt △ABC 中,∠C =90° 正弦:斜边的对边A A ∠=sin ;c a A =sin 余弦:斜边的邻边A A ∠=cos ;c b A =cos 正切:的邻边的对边A tan ∠∠=A A ;b a A =tan 根据定义,写出∠B 的三个三角函数值 =B sin ___________;=B cos ____________;=B tan _______________;2.三角函数之间关系(1)同角三角函数关系AA A cos sin tan =;1cos sin 22=+A A (2)互余角三角函数关系(A +B =90)B A cos sin =;B A sin cos =;tanA ·tanB =1 一个角的正弦等于它余角的余弦;一个角的余弦等于它的余角的正弦3.特殊角的三角函数值30°、45°、60°例题1:计算(1)22sin45°+sin60°-2cos45°; (2)(1+2)0-|1-sin30°|+(21)-1;(3)sin60°+︒-60tan 11; (4)2-3-(0032+π)0-cos60°-211-.4.例题2:会设计并根据三角函数关系计算15°、75°角的三角函数练习:1.求证:22365.37tan 0--+=2.求︒18sin 的值5.根据表格中数据总结正弦、余弦、正切的增减性当0°≤α≤90°时,sin α随α的增大而_______;cos α随α的增大而_______;tan α随α的增大而_______6.已知一个三角函数值,求其他三角函数值。
(根据三角函数关系)例题3:sinA =52,求cosA 、tanA例题4:α为锐角,若sin α<23,求α的范围 α为锐角,若cos α<23,求α的范围例题5:已知sin α+cos α=45,求sin α·cos α的值练习:1.化简ααcos sin 21⋅-2. 已知45°<α<90°,16173cos sin =⋅αα,求αsin。


比赛讲座 33-三角函数几何中的两个基本量是:线段的长度和角的大小. 三角函数的实质就是用线段长度之比来表示角的大小,进而将两个基本量联系在一同,使我们能够借助三角变换或三角计算来解决一些较难的几何问题. 三角函数不单是一门风趣的学识,并且是解决几何问题的有力工具. 1.角函数的计算和证明问题在解三角函数问题以前,除了熟知初三教材中的相关知识外,还应当掌握:(1)三角函数的单一性当a为锐角时,sina与tga的值随a的值增大而增大;cosa与ctga 随 a 的值增大而减小;当 a 为钝角时,利用引诱公式转变为锐角三角函数议论.注意到 sin45 °=cos45°=, 由 (1) 可知 , 当时 0< a<45°时 ,cosa > sina; 当 45°< a<90°时 ,cosa < sina.(2)三角函数的有界性 |sina| ≤1,|cosa| ≤1,tga 、 ctga 可取随意实数值(这一点可直接利用三角函数定义导出) .例 1( 1986 年全国初中数学比赛备用题)在△ABC 中,假如等式sinA+cosA=建立,那么角A是()(A)锐角(B)钝角(C)直角剖析对 A 分类,联合sinA 和 cosA 的单一性用列举法议论.解当 A=90°时, sinA 和 cosA=1;当 45°< A<90°时 sinA >,cosA>0,∴s inA+cosA>当 A=45°时, sinA+cosA=当 0< A<45°时, sinA > 0,cosA >∴sinA+cosA>∵1,都大于.∴裁减( A)、( C),选( B) .例 2( 1982 年上海初中数学比赛题)ctg67 °30′的值是()(A)-1(B)2-(C)-1(D)( E)剖析结构一个有一锐角恰为67°30′的 Rt△,再用余切定义求之.D 使 AD=AC,连DC,则解如图 36-1 ,作等腰 Rt△ABC,设∠ B=90°, AB=BC=1.延伸 BA到AD=AC= ,∠ D=22.5°, ∠DCB=67.5°. 这时,ctg67 °30′=ctg ∠DCB=∴选 (A).例 3(1990 年南昌市初中数学比赛题 ) 如图 , 在△ ABC中, ∠A所对的 BC边的边长等于 a, 旁切圆⊙O的半径为 R, 且分别切 BC及 AB、 AC的延伸线于 D, E,F. 求证 :R≤a·O′, 分别切三边于G,H,K. 由对称性知GE=KF(如图36-2).设 GB=a,证明作△ ABC的内切圆BE=x, KC=y,CF=b. 则x+a=y+b,①且 BH=a,BD=x,HC=y,DC=b.于是 ,x-a=y-b.②①+②得 ,x=y. 进而知 a=b.∴G E=BC=a.设⊙ O′半径为r. 明显 R+r≤OO′ ( 当 AB=AC)时取等 .作 O′M⊥EO 于 M,则 O′M=GE=a,∠OO′M=∴R+r≤两式相加即得R≤.例 4( 1985 年武汉等四市初中联赛题)凸4n+2 边形 A A A A( n 为自然数)各内角都是1234n+230°的整数倍,已知对于x 的方程:x 212=0①+2xsinA +sinAx2+2xsinA 2+sinA 3=0②x2+2xsinA 3+sinA 1=0③都有实根,求这凸4n+2 边形各内角的度数 .解∵各内角只好是、、、,∴正弦值只好取当 sinA 1=时,∵ sinA2≥sinA 3≥∴方程①的鉴别式△1 =4(sin2A1-sinA 2)≤440方程①无实根,与已知矛盾,故sinA 1≠.当 sinA 1=时,sinA2≥,sinA3≥,∴方程①的鉴别式△=4( sin A -sinA) =0.1212方程①无实根,与已知矛盾,故sinA 1=.综上所述,可知sinA 1=1, A1=.同理, A2=A3=.这样其他4n-1 个内角之和为这些角均不大于又 n 为自然数,∴n=1, 凸 n 边形为 6 边形 , 且A4+A5 +A6=4×2.解三角形和三角法定理推论设a、 b、 c、 S 与 a′、 b′、 c′、 S′. 若我们在正、余弦定理以前介绍上述定理和推论是为了在解三角形和用三角函数解几何题时有更大的自由 .(1)解三角形例 5(第 37 届美国中学生数学比赛题)在图 36-3 中,AB是圆的直径, CD是平行于 AB的弦,且AC和 BD订交于 E,∠ AED=α , △CDE和△ ABE的面积之比是 ( ).22(A)cos α (B)sin α (C)cos α (D)sinα (E)1-sin α解如图,由于AB∥DC,AD=CB,且△ CDE∽△ ABE,BE=AE,所以连接 AD,由于 AB是直径,所以∠ ADB=在直角三角形ADE中, DE=AEcosα .∴应选 (C).例 6(1982年上海初中数学比赛题) 如图 36-4, 已知 Rt△斜边 AB=c,∠A=α , 求内接正方形的边长.解过 C作 AB的垂线 CH,分别与GF、 AB 交于 P、 H,则由题意可得又∵△ ABC∽△ GFC,∴,即(2)三角法.利用三角知识(包含下一讲介绍的正、余弦定理)解几何问题的方法叫三角法. 其特色是将几何图形中的线段,面积等用某些角的三角函数表示,经过三角变换来达到计算和证明的目的,思路简单,进而减少几何计算和证明中技巧性很强的作协助线的困难 .例 7( 1986 年全国初中数学比赛搜集题)如图36-5 ,在△ ABC中, BE、 CF是高,∠ A=,则△ AFE 和四边形FBCE的面积之比是()(A)1∶2( B)2∶3( C)1∶1( D)3∶4解由 BE、 CF 是高知 F、B、 C、 E 四点共圆,得AF·AB=AE·AC.在 Rt△ABE中,∠ ABE=,∴S△AFE∶S FBCE=1∶1.应选(C).例 8(1981年上海中学生数学比赛题) 在△ ABC中∠C为钝角 ,AB 边上的高为h, 求证 :AB >2h.证明如图 36-6,AB=AD+BD=h(ctgA+ctgB)①∵∠C是钝角 , ∴∠ A+∠B<, ∴ctgB > ctg(- A)=tgA. ②由①、②和代数基本不等式,得例9(第一组对边与一条对角线之长的和为18 届国际数学比赛题)已知面积为32cm2的平面凸四边形中16cm.试确立另一条对角线的全部可能的长度.解如图36-7 ,设四边形ABCD面积S 为32cm2,并设AD=y,AC=x,BC=z. 则x+y+z=16(cm)由但 S=32,∴ sin θ =1,sin=1, 且 x-8=0. 故θ = =且x=8,y+z=8. 这时易知另一条对角线BD的长为此处无图例 10(1964年福建中学数学比赛题) 设 a、b、c 是直角三角形的三边, c 为斜边,整数n≥3, 求证 :a n+b n< c n.剖析如图为三角不等式34-8,sin注意到nα+cosRt△ABC的边角关系nα< 1 来议论 .:a=csinα> 0,b=ccosα> 0, 可将不等式转变证明设直角三角形一锐角∠BAC= α ( 如图 ),则。

三角函数及其应用三角是代数与几何联系的“桥梁”,同时三角也是解决某些代数、几何问题的工具. ☆三角与代数☆ 【例1】求证:20720sin 31<︒<. 证明:证法1:由)2,0(,sin π∈<x x x ,20799sin20sin <<=︒ππ, 由)6,0(,3sin ππ∈>x x x ,31939sin 20sin =⨯>=︒πππ. 证法2:2320sin 420sin 360sin 3=︒-︒=︒,设x =︒20sin ,则023343=+-x x ,设2334)(3+-=x x x f ,21,0312)(2±==-='x x x f ,∴函数)(x f y =单调区间)21,(--∞↗,)21,21(-↘,),21(+∞↗,又∵2120sin 0<︒<,及0231274)31(>+-=f ,02757.13)207(<-=f ,∴20720sin 31<︒<. 【补充】求证:9210tan 61<︒<【练习】N n ∈,2≥n ,求证:321cos 31cos 21cos>⋅⋅n . 证明:∵121311110<<<<-<<n n , ∴kk 11sin0<<, ∴n k k k k k k k ,,3,2,)1)(1(111sin 11cos 2222=+-=->-=. ∴)11()4543()3432()2321()1cos 31cos 21(cos2nn n n n +⋅-⋅⋅⋅⋅⋅>⋅⋅ 2)32(21121>>+=n n ,∴321cos 31cos 21cos>⋅⋅n . 【例2】C B A ,,为锐角△ABC 的三个内角,求证:233sin sin sin 2≤++<C B A . 证法1:因为x y sin =在区间)2,0(π上为上凸函数,由琴生(Jensen)不等式得2333sin3sin sin sin =++≤++C B A C B A , 又由)2,0(,2sin ππ∈>x x x 得,2)(2sin sin sin =++>++C B A C B A π.证法2:C BA CB A B AC B A sin 2sin 2sin 2cos 2sin2sin sin sin ++≤+-+=++ .233)46(332)2sin 1)(2sin 33(332)2sin 1(2cos 2)2sin 1(2cos 24322=≤+-=+=+=C C C C C CC B A ,,为锐角△ABC 的三个内角,不妨设C B A ≥≥,∴C B A C B A <-+<,,2cos 2cos ,22CB AC B A >-<-, ∴C CB AC B A B A C B A sin 2cos 2sin 2sin 2cos 2sin 2sin sin sin ++>+-+=++ 2sin cos 1sin 2cos 22>++=+=C C C C.【练习】C B A ,,为锐角△ABC 的三个内角,求证:23cos cos cos 1≤++<C B A .证明:C B A B A C B A cos 2cos 2cos 2cos cos cos +-+=++C BA cos 2cos 2++≥ 2323)212(sin 22sin 212sin 222≤+--=-+=C C C ,2)(cos 2cos 2)2cos(2cos B A B A B A +-+=-++πππ,2cos 2cos 2cos cos BA B A B A -+=+,<-2B A 2)(B A +-π, ∴2cos 2)(cos 2cos CB A B A =+->-π,∴C CC B A B A B A sin 2cos 2sin 22cos 2cos2cos cos =>-+=+, ∴1cos sin cos cos cos >+>++C C C B A .【例3】已知1),1,0(,,=++∈ca bc ab c b a ,求证:4331111222≤+++++<cc b b a a .证明:方法1:由已知1),1,0(,,=++∈ca bc ab c b a ,可设2tan ,2tan ,2tanC c B b A a ===, 其中C B A ,,为锐角△ABC 的三个内角,则A A A a a sin 212tan 12tan122=+=+,B B B b b sin 212tan 12tan 122=+=+,C C C c c sin 212tan 12tan122=+=+, 原不等式等价于233sin sin sin 2≤++<C B A ,证法见例2.方法2:))()(())((122c b c a b a acab c a b a a bc ac ab a a a a ++++=++=+++=+,=+++++222111c c b b a a ))()((2c b c a b a +++, 只需证433))()((21≤+++<c b c a b a ,即2))()((938<+++≤c b c a b a . 由1),1,0(,,=++∈ca bc ab c b a ,可知3≥++c b a ,只需证加强不等式))()((9))((8c b c a b a ca bc ab c b a +++≤++++,即)2(9)3(8222222222222b c a c a b c b c a b a abc b c a c a b c b c a b a abc ++++++≤++++++,即≤abc 6b c a c a b c b c a b a 222222+++++,由均值可知显然成立.【练习】已知abc c b a c b a =++>,0,,,求证:231111111222≤+++++<cb a .提示:设C c B b A a tan ,tan ,tan ===,原不等式等价于23cos cos cos 1≤++<C B A .【变式】已知1),,0(,,=+++∞∈ca bc ab c b a ,求证:231111222≤+++++<cc b b a a .提示:设2tan ,2tan ,2tan C c B b A a ===,原不等式等价于232sin 2sin 2sin 1≤++<C B A .(或将c b a ,,分别替换为cb a 1,1,1将变为上面练习.) 【例4】设12π≥≥≥z y x ,且2π=++z y x ,求乘积z y x cos sin cos 的最大值和最小值.)12,245.(83246cos 142cos 1cos 21cos )sin(21cos )]sin()[sin(21cos sin cos 2πππ===+=+≤+==+≤--+=z y x z zz y x z y x y x z y x)12,3.(81432cos142cos 1cos 21)sin(cos 21)]sin()[sin(cos 21cos sin cos 2πππ====+≥+==+≥-++=z y x x xz y x z y z y x z y x 【练习】设C B A ,,是三角形的三个内角,求证:3233sin 3sin 3sin 2≤++<-C B A ,并确定其中的等号何时成立.解析:不妨设︒≥60A ,则︒≤+120C B ,从而︒≤+<-≤︒180)(23||230C B C B , 由此可得)(23c o s )(23c o s C B C B +>-.再由0)(23s i n ≥+C B ,得到)(23cos )(23sin 2)(23cos )(23sin 2C B C B C B C B ++≥-+,即)(3sin 3sin 3sin C B C B +≥+,于是2)(3sin 3sin 3sin 3sin 3sin -≥++≥++C B A C B A , 为使23sin 3sin 3sin -=++C B A ,必须满足1)(3sin 3sin -=+=C B A ,0)(23sin =+C B ,这是不可能的,从而23sin 3sin 3sin ->++C B A . 另一方面,由︒≥60A 可知,)(23cos )(23sin 23sin 3sin 3sin 3sin C B C B A C B A -++=++)(23sin 23sin C B A ++≤A A 23cos 23sin -=A A 23cos )123(sin 2-=33)23sin 1)(323sin 3(312)23sin 1)(123(sin 2A A A A -+=-+=323)46(3124=≤. 当且仅当,1)(23cos ),23sin 1()323sin 3(=--=+C B A A即︒==︒=20,140C B A 时,等号成立.【例5】对于任意的正数x 、y 、z 、及△ABC 三内角A 、B 、C ,总有:C xy B zx A yz z y x cos 2cos 2cos 2222++≥++.证明:0)sin sin ()cos cos (sin sin 2sin sin )cos cos (cos cos 2cos cos cos 2)cos cos (cos 2cos 2cos 2),,(22222222222222222≥-+--=-++--=----++--=---++=B z C y C y B z x C B yz B z C y C y B z x C B yz C y B z A yz z y C y B z x Cxy B zx A yz z y x z y x f ∴C xy B zx A yz z y x cos 2cos 2cos 2222++≥++.【补充】求证:02cos 22cos 22cos 2222≥+++++C xy B zx A yz z y x【变式】求证:)(21cos cos cos zxy y zx x yz C z B y A x ++≤++ 求证:23cos cos cos ≤++C B A 求证:C ab B ca A bc c b a cos 2cos 2cos 2222++=++求证:C B A B A C A C B C B A cos sin sin 2cos sin sin 2cos sin sin 2sin sin sin 222++=++求证:)(21cos cos cos cabb ac a bc C c B b A a ++≤++ 【练习】给定正整数n ,求最小的正数λ,使得对于任何=i θ),,2,1)(2,0(n i =π,只要2212tan tan tan nn =⋅⋅⋅θθθ ,就有n θθθcos cos cos 21+++ 不大于λ.解析:1°当2,1=n 时,=λ33n , 当1=n 时,33cos ,2tan 11==θθ,当2=n 时,,2tan tan 21=θθ设x =12tan θ,则x4tan 22=θ, xx 41111tan 11tan 11cos cos 221221+++=+++=+θθθθ x x xx x x x x x x x x 45345214545242411112++-+++=+++++++=⎪⎪⎪⎪⎭⎫⎝⎛+++设]31,0(451∈=++t xx ,则341234111122≤++-=⎪⎪⎪⎪⎭⎫⎝⎛+++t t x x , =+21cos cos θθ33241111≤+++xx,当2=x 即21θθ=时取等号. 2°当3≥n 时,1-=n λ,先证1cos cos cos 21-<+++n n θθθ ①不妨设n θθθθ≥≥≥≥ 321,要证明①式成立,只要证2cos cos cos 321<++θθθ,②2212tan tan tan n n =⋅⋅⋅θθθ ,故22tan tan tan 321≥⋅⋅θθθ.2sin 1sin 1cos 22ii i θθθ-<-=,32322232sin sin 22sin sin 2cos cos θθθθθθ-≤+-<+,322212322212tan tan 81cos 1,tan tan 8tan θθθθθθ+≥∴≥, 32223222323222321sin sin cos cos 8sin sin tan tan 8tan tan cos θθθθθθθθθθθ+=+≤,)sin sin cos cos 811(sin sin 2cos cos cos 3222322232321θθθθθθθθθ+--<++2cos cos cos 321<++θθθ,⇔1sin sin cos cos 832223222≥+θθθθ⇔)tan 1)(tan 1(sec sec tan tan 8322232223222θθθθθθ++=≥+ ⇔7tan tan 3222≤+θθ ③.若③式成立,则②式成立.AB CP若③式不成立,即7tan tan 3222>+θθ,从而27tan tan 2212>≥θθ,32cos cos 21<≤θθ,21322cos cos cos 321<+<++θθθ.从而①式得证. 现证1-=n λ为最小的.事实上,若10-<<n λ,则取11<-=n a λ,从而存在,,,2,1)2,0(n i i =∈πθ使得)1,,2,1(1tan ,cos 2-=-==n i a a a i i θθ,1221(2tan --=n nn a aθ从而2212tan tan tan nn =⋅⋅⋅θθθ ,但λθθθθθθ=+++>+++-12121cos cos cos cos cos cos n n , 当3≥n 时,最小的正数λ为1-n .综上所求最小正数⎪⎩⎪⎨⎧≥-==)3(,1)2,1(,33n n n n λ.【练习】设8,0,0,0=>>>abc c b a ,求证:21111111<+++++<cb a .☆三角与几何☆【例6】已知点P 是锐角△ABC 内一点,使得∠PAB =∠PBC =∠PCA .求证:C B A PAB cot cot cot cot ++=∠. 证明:证法1:设z PC y PB x PA ===,,,∠PAB =∠PBC =∠PCA =θ则θcos 2222xc c x y -+= θcos 2222ya a y z -+= θcos 2222zb b z x -+=)(cos 2222cx bz ay c b a ++=++θ,又)(sin 21cx bz ay S ABC++=∆θ,∴ABCS c b a ∆++=4cot 222θ, Rabc c b a R a bc a c b CC B B A A C B A 4422sin cos sin cos sin cos cot cot cot 222222⨯++=⋅-+=++=++∑,RabcC ab S ABC 4sin 21==∆,∴C B A PAB cot cot cot cot ++=∠.证法2:由角元式赛瓦(Ceva )定理得1)sin(sin )sin(sin )sin(sin =-⋅-⋅-θθθθθθC B A ,1)cos cot )(sin cos cot )(sin cos cot (sin =---C C B B A A θθθ,01)cos (cot )cos cos sin (cot )cos sin sin (cot )sin (23=--+-∏∑∑∏A C B A C B A A θθθ由C B A C B A C B A C B A sin sin sin sin cos cos cos sin cos cos cos sin =++, C B A C B A C B A C B A cos cos cos 1cos sin sin sin cos sin sin sin cos +=++得 0)1)cos ((cot )sin (cot )1)cos ((cot )sin (23=+-++-∏∏∏∏A A A A θθθ0)1))(cot 1)cos ((cot )sin ((2=++-∏∏θθA A , 0)1)cos ((cot )sin (=+-∏∏A A θ,CB A CB A CB AC B A C B A AA cot cot cot sin sin sin cos sin sin sin cos sin sin sin cos sin 1)cos (cot ++=++=+=∏∏θ 证法3:(平面几何证法)略【练习】设P 为△ABC 内或边界上一点,点P 到三边的距离为PD 、PE 、PF .求证:)(2PF PE PD PC PB PA ++≥++.BPF C PE B PF C PE B PF C PE C B PEPF C B PEPF PF PE C B PEPF PF PE EF A PA sin sin )cos cos ()sin sin (sin sin 2cos cos 2)cos(2sin 222222+≥-++=+-+=+-+== ∴A BPF A C PE PA sin sin sin sin +≥, 同理B C PD B A PF PB sin sin sin sin +≥,CAPE C B PD PC sin sin sin sin +≥, )(2)sin sin sin sin ()sin sin sin sin ()sin sin sin sin (PF PE PD B AA B PF C A A C PE C B B C PD PC PB PA ++≥+++++≥++ 【补充】H 为锐角△ABC 的垂心,F E D ,,为垂足,求证:(1)垂足△DEF 的周长)(21cos cos cos c b a C c B b A a ++≤++=; (2)H 为垂足△DEF 的内心;(3)九点圆半径为外接圆半径的一半。

年级:高中学科:数学课时:2课时教学目标:1. 让学生掌握三角函数的基本概念和性质,包括正弦、余弦、正切函数的定义、周期性、奇偶性、周期性等。
2. 培养学生的逻辑思维能力和解题技巧,提高学生运用三角函数解决实际问题的能力。
3. 激发学生对数学的兴趣,培养学生的团队协作精神。
教学重点:1. 三角函数的基本概念和性质2. 解三角函数方程和不等式教学难点:1. 三角函数方程和不等式的解法2. 解题技巧和策略教学过程:第一课时一、导入1. 回顾初中阶段学习的三角函数知识,引导学生思考三角函数在高中数学中的重要性。
2. 引出本节课的学习内容:竞赛三角函数。
二、新课讲解1. 正弦、余弦、正切函数的定义:以单位圆为基础,介绍正弦、余弦、正切函数的定义,讲解函数的几何意义。
2. 周期性:讲解三角函数的周期性,并举例说明。
3. 奇偶性:讲解三角函数的奇偶性,并举例说明。
4. 三角函数的诱导公式:介绍诱导公式,讲解公式的推导过程和应用。
三、课堂练习1. 基本概念和性质的应用:让学生完成相关练习题,巩固所学知识。
2. 课堂讨论:引导学生讨论三角函数在实际问题中的应用。
四、课堂小结1. 总结本节课的学习内容,强调重点和难点。
2. 布置课后作业,巩固所学知识。
第二课时一、复习导入1. 复习上一节课所学内容,检查学生对基本概念和性质的理解。
2. 引导学生思考如何运用三角函数解决实际问题。
二、新课讲解1. 三角函数方程和不等式的解法:讲解三角函数方程和不等式的解法,介绍解题技巧和策略。
2. 实际问题中的应用:举例说明三角函数在实际问题中的应用,如物理、工程、经济等领域。
三、课堂练习1. 解三角函数方程和不等式:让学生完成相关练习题,巩固所学知识。
2. 课堂讨论:引导学生讨论三角函数在实际问题中的应用。
四、课堂小结1. 总结本节课的学习内容,强调重点和难点。
2. 布置课后作业,巩固所学知识。
教学评价:1. 通过课堂练习和课后作业,了解学生对三角函数知识的掌握程度。
2019-2020年高考数学竞赛三角函数教案讲义(6)一、基础知识定义1 角,一条射线绕着它的端点旋转得到的图形叫做角。
若旋转方向为逆时针方向,则角为正角,若旋转方向为顺时针方向,则角为负角,若不旋转则为零角。
角的大小是任意的。
定义2 角度制,把一周角360等分,每一等价为一度,弧度制:把等于半径长的圆弧所对的圆心角叫做一弧度。
360度=2π弧度。
若圆心角的弧长为L,则其弧度数的绝对值|α|=,其中r是圆的半径。
定义3 三角函数,在直角坐标平面内,把角α的顶点放在原点,始边与x轴的正半轴重合,在角的终边上任意取一个不同于原点的点P,设它的坐标为(x,y),到原点的距离为r,则正弦函数s inα=,余弦函数co sα=,正切函数tanα=,余切函数cotα=,正割函数se cα=,余割函数c s cα=定理1 同角三角函数的基本关系式,倒数关系:tanα=,s inα=,co sα=;商数关系:tan α=;乘积关系:tanα×co sα=s inα,cotα×s inα=co sα;平方关系:s in2α+co s2α=1, tan2α+1=se c2α, cot2α+1=c s c2α.定理2 诱导公式(Ⅰ)s in(α+π)=-s inα, co s(π+α)=-co sα, tan(π+α)=tanα, cot(π+α)=cotα;(Ⅱ)s in(-α)=-s inα, co s(-α)=co sα, tan(-α)=-tanα, cot(-α)=cotα; (Ⅲ)s in(π-α)=s inα, co s(π-α)=-co sα, tan=(π-α)=-tanα, cot(π-α)=-cotα; (Ⅳ)s in=co sα, co s=s inα, tan=cotα(奇变偶不变,符号看象限)。
定理3 正弦函数的性质,根据图象可得y=s inx(x∈R)的性质如下。
单调区间:在区间上为增函数,在区间上为减函数,最小正周期为2. 奇偶数. 有界性:当且仅当x=2kx+时,y 取最大值1,当且仅当x=3k-时, y取最小值-1。
三角函数专题一、核心知识点归纳:1、正弦函数、余弦函数和正切函数的图象与性质:sin y x =cos y x =tan y x =图象定义域 R R,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭值域[]1,1-[]1,1-R最值当22x k ππ=+()k ∈Z 时,max 1y =; 当22x k ππ=-()k ∈Z 时,min 1y =-. 当()2x k k π=∈Z 时,max 1y =;当2x k ππ=+()k ∈Z 时,min 1y =-.既无最大值也无最小值周期性 2π2ππ奇偶性奇函数 偶函数奇函数单调性在2,222k k ππππ⎡⎤-+⎢⎥⎣⎦()k ∈Z 上是增函数;在32,222k k ππππ⎡⎤++⎢⎥⎣⎦ ()k ∈Z 上是减函数.在[]()2,2k k k πππ-∈Z 上是增函数;在[]2,2k k πππ+ ()k ∈Z 上是减函数. 在,22k k ππππ⎛⎫-+ ⎪⎝⎭()k ∈Z 上是增函数.对称性对称中心()(),0k k π∈Z对称中心对称中心函 数 性 质2。
正、余弦定理:在ABC ∆中有: ①正弦定理:2sin sin sin a b cR A B C===(R 为ABC ∆外接圆半径) 2sin 2sin 2sin a R A b R B c R C =⎧⎪=⎨⎪=⎩⇒ sin 2sin 2sin 2a A Rb B Rc C R⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩注意变形应用 ②面积公式:111sin sin sin 222ABC S abs C ac B bc A ∆=== ③余弦定理: 2222222222cos 2cos 2cos a b c bc A b a c ac B c a b ab C ⎧=+-⎪=+-⎨⎪=+-⎩ ⇒ 222222222cos 2cos 2cos 2b c a A bc a c b B ac a b c C ab ⎧+-=⎪⎪+-⎪=⎨⎪⎪+-=⎪⎩二、方法总结:1.三角函数恒等变形的基本策略。
第十六讲 锐角三角函数古希腊数学家和古代中国数学家为了测量的需要,他们发现并经常利用下列几何结论:在两个大小不同的直角三角形中,只要有一个锐角相等,那么这两个三角形的对应边的比值一定相等.正是古人对天文观察和测量的需要才引起人们对三角函数的研究,1748年经过瑞士的著名数学家欧拉的应用,才逐渐形成现在的sin 、cos 、tg 、ctg 的通用形式.三角函数揭示了直角三角形中边与锐角之间的关系,是数形结合的桥梁之一,有以下丰富的性质:1.单调性;2.互余三角函数间的关系;3.同角三角函数间的关系.平方关系:sin 2α+cos 2α=1;商数关系:tg α=ααcos sin ,ctg α=ααsin cos ; 倒数关系:tg αctg α=1.【例题求解】【例1】 已知在△ABC 中,∠A 、∠B 是锐角,且sinA =135,tanB=2,AB=29cm , 则S △ABC = .思路点拨 过C 作CD ⊥AB 于D ,这样由三角函数定义得到线段的比,sinA=135=AC CD ,tanB=2=BDCD ,设CD=5m ,AC =13m ,CD =2n ,BD =n ,解题的关键是求出m 、n 的值. 注:设△ABC 中,a 、b 、c 为∠A 、∠B 、∠C 的对边,R 为△ABC 外接圆的半径,不难证明:与锐角三角函数相关的几个重要结论:(1) S △ABC =C ab B ac A bc sin 21sin 21sin 21==; (2)R Cc B b A a 2sin sin sin ===. 【例2】 如图,在△ABC 中.∠ACB =90°,∠ABC =15°,BC=1,则AC=( )A .32+B .32-23-思路点拨 由15°构造特殊角,用特殊角的三角函数促使边角转化.注:(1)求(已知)非特角三角函数值的关是构造出含特殊角直角三角形.(2)求(已知)锐角角函数值常根据定转化为求对应线段比,有时需通过等的比来转换.【例3】 如图,已知△ABC 是等腰直角三角形,∠ACB =90°,过BC 的中点D 作DE ⊥AB 于E ,连结CE ,求sin ∠ACE 的值.思路点拨 作垂线把∠ACE 变成直角三角形的一个锐角,将问题转化成求线段的比.【例4】 如图,在△ABC 中,AD 是BC 边上的高,tanB=cos ∠DAC ,(1)求证:AC =BD ;(2)若sinC=1312,BC=12,求AD 的长. 思路点拨 (1)把三角函数转化为线段的比,利用比例线段证明;(2) sinC=ACAD =1312,引入参数可设AD=12k ,AC =13k .【例5】 已知:在Rt △ABC 中,∠C=90°,sinA 、sinB 是方程02=++q px x 的两个根.(1)求实数p 、q 应满足的条件;(2)若p 、q 满足(1)的条件,方程02=++q px x 的两个根是否等于Rt △ABC 中两锐角A 、B的正弦?思路点拨 由韦达定理、三角函数关系建立p 、q 等式,注意判别式、三角函数值的有界性,建立严密约束条件的不等式,才能准确求出实数p 、q 应满足的条件.学历训练1.已知α为锐角,下列结论①sin α+cos α=l ;②如果α>45°,那么sin α>cos α;③如果cos α>21 ,那么α<60°; ④αsin 11)-(sin 2-=α.正确的有 . 2.如图,在菱形ABCD 中,AE ⊥BC 于E ,BC=1,cosB 135,则这个菱形的面积为 . 3.如图,∠C=90°,∠DBC=30°,AB =BD ,利用此图可求得tan75°= .4.化简(1)263tan 27tan 22-+ = .(2)sin 2l °+sin 22°+…+sin 288°+sin 289°= .5.身高相等的三名同学甲、乙、丙参加风筝比赛.三人放出风筝线长、线与地面夹角如下表(假设风筝线是拉直的),则三人所放的风筝中( )A .甲的最高B .丙的最高C .乙的最低D .丙的最低6.已知 sin αcos α=81,且0°<α<45°则co α-sin α的值为( ) A .23 B .23- C .43 D .43- 7.如图,在△ABC 中,∠C =90°,∠ABC =30°,D 是AC 的中点,则ctg ∠DBC 的值是( )A .3B .32C . 23D .43 8.如图,在等腰Rt △ABC 中.∠C =90°,AC =6,D 是AC 上一点,若tan ∠DBA=51,则AD 的长为( )A .2B .2C . 1D .229.已知关于x 的方程0)1(242=++-m x m x 的两根恰是某直角三角形两锐角的正弦,求m 的值.10.如图,D 是△ABC 的边AC 上的一点,CD=2AD ,AE ⊥BC 于E ,若BD =8,sin ∠CBD=43,求AE 的长.11.若0°<α<45°,且sin αcon α=1673,则sin α= . 12.已知关于x 的方程0)cos 1(2sin 423=-+⋅-ααx x 有两个不相等的实数根,α为锐角,那么α的取值范围是 .13.已知是△ABC 的三边,a 、b 、c 满足等式))((4)2(2a c a c b -+=,且有035=-c a ,则sinA+sinB+sinC 的值为 .14.设α为锐角,且满足sin α=3cos α,则sin αcos α等于( )A .61B .51 C .92 D .103 15.如图,若两条宽度为1的带子相交成30°的角,则重叠部分(图中阴影部分)的面积是( )A .2B .23 C .1 D .21 16.如图,在△ABC 中,∠A =30°,tanB=23,AC=32,则AB 的长是( ) A .33+ B .322+ C .5 D .29 17.己在△ABC 中,a 、b 、c 分别是∠A 、∠B 、∠C 的对边,且c=35,若关于x 的方程0)35(2)35(2=-+++b ax x b 有两个相等的实根,又方程0sin 5)sin 10(22=+-A x A x 的两实根的平方和为6,求△ABC 的面积.18.如图,已知AB=CD=1,∠ABC =90°,∠CBD °=30°,求AC 的长.19.设 a 、b 、c 是直角三角形的三边,c 为斜边,n 为正整数,试判断n n b a +与n c 的关系,并证明你的结论.20.如图,已知边长为2的正三角形ABC 沿直线l 滚动.(1)当△ABC 滚动一周到△A l B 1C 1的位置,此时A 点所运动的路程为 ,约为 π(2)设△ABC 滚动240°,C 点的位置为C ˊ,△ABC 滚动480°时,A 点的位置在A ˊ,请你利用三角函数中正切的两角和公式tan(α+β)=(tan α+tan β)÷(1-tan α·tan β),求出∠CAC ˊ+∠CAA ˊ的度数.参考答案。