计算理论难解..

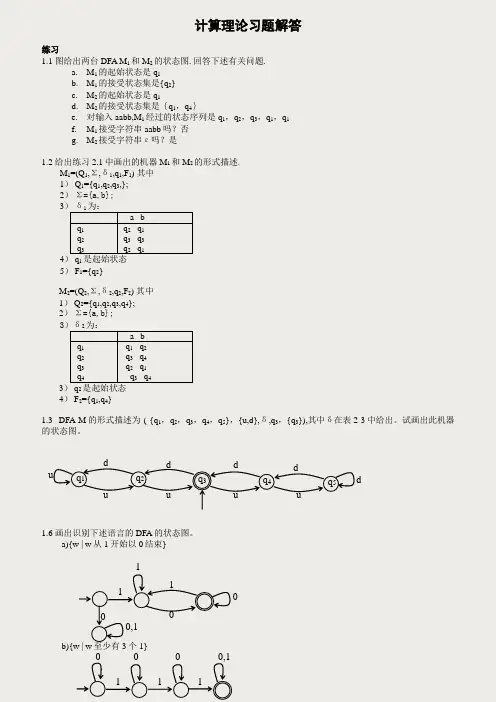
计算理论习题解答练习1.1 图给出两台DFA M 1和M 2的状态图. 回答下述有关问题.a. M 1的起始状态是q 1b. M 1的接受状态集是{q 2}c. M 2的起始状态是q 1d. M 2的接受状态集是｛q 1，q 4｝e. 对输入aabb,M 1经过的状态序列是q 1，q 2，q 3，q 1，q 1f. M 1接受字符串aabb 吗？否g. M 2接受字符串ε吗？是1.2 给出练习2.1中画出的机器M 1和M 2的形式描述.M 1=(Q 1,Σ,δ1,q 1,F 1) 其中 1） Q 1={q 1,q 2,q 3,}; 2） Σ={a,b}; 3） δ1为：a b q 1 q 2 q 3 q 2 q 1 q 3 q 3 q 2 q 1 4） q 1是起始状态 5） F 1={q 2}M 2=(Q 2,Σ,δ2,q 2,F 2) 其中 1） Q 2={q 1,q 2,q 3,q 4}; 2） Σ={a,b}; 3）δ2为：a b q 1 q 2 q 3 q 4 q 1 q 2 q 3 q 4 q 2 q 1 q 3 q 4 3） q 2是起始状态 4） F 2={q 1,q 4}1.3 DFA M 的形式描述为 ( {q 1，q 2，q 3，q 4，q 5}，{u,d},δ,q 3，{q 3}),其中δ在表2-3中给出。

试画出此机器的状态图。

1.6 画出识别下述语言的DFA 的状态图。

a){w | w 从1开始以0结束}b){w | w 至少有3个1}q 1 q 5 q 4 q 2 q 3 ud u u u u d d d d 00 1 11 0,1 0 0 1 0 0 1 10,1c) {w | w 含有子串0101}d) {w | w 的长度不小于3，且第三个符号为0}e) {w | w 从0开始且为奇长度，或从1开始且为偶长度}或f) {w | w 不含子串110}g) {w | w 的长度不超过5}h){w | w 是除11和111以外的任何字符}i){w | w 的奇位置均为1}j) {w | w 至少含有2个0，且至多含有1个1}k) {ε,0}l) {w | w 含有偶数个0，或恰好两个1}0,110 0 1 110 0,1 00,1 0,1 1 1 0,1 0 0,10,1 0,1 00,11 0,10 0,1 10,1 0111 00,1 0,1 0,1 0,1 0,10,10,11 1 1 0,1 0 0 00 0 10 0 1 11 1 1 0 0 0,1 0 0,1 0,11 1 00,1 0,1 1 01 1 0 0 0 0 0 0 1m) 空集 n) 除空串外的所有字符串1.7 给出识别下述语言的NFA ，且要求符合规定的状态数。

可计算性与计算复杂性1.可计算性：可计算性研究的是什么样的问题可以通过其中一种计算模型解决。

早期的计算模型是图灵机（Turing machine），后来发展出其他等效的计算模型，例如递归函数、Lambda演算等。

根据这些计算模型，可以定义一类问题为可计算问题，也就是可以通过计算模型求解的问题。

1.1停机问题：停机问题是可计算性的典型例子，它是指根据给定的程序和输入，判断这个程序是否会在有限的时间内停止运行。

根据图灵在20世纪30年代证明的停机问题的不可判定性，他证明了不存在一个通用的算法能够判断任意程序是否停机，这个结论被称为图灵不可判定性定理。

1.2基本计算问题：除了停机问题，可计算性还研究了一些其他的基本计算问题。

例如，可计算性研究了自动机是否可以接受一些字符串，或者函数是否可以被一个特定的计算模型计算等。

1.3计算模型的等效性：在可计算性理论中，研究了不同计算模型之间的等效性。

图灵机、递归函数和Lambda演算等计算模型之间可以相互转化，这意味着它们的计算能力是等价的。

这个等价性的概念对理解可计算性是至关重要的。

2.计算复杂性：计算复杂性研究的是什么样的问题可以在多项式时间内解决，以及在不同条件下求解问题所需要的计算资源（例如时间、空间等）。

计算复杂性理论的核心是研究问题的复杂度类别和难度。

2.1多项式时间可解问题：计算复杂性理论将问题分为多项式时间可解问题和非多项式时间可解问题。

多项式时间可解问题是指那些可以在多项式时间内求解的问题。

这些问题的解决方法被认为是高效的，因为随着输入规模的增加，所需计算资源的增长是可接受的。

2.2难解问题：非多项式时间可解问题是那些不可以在多项式时间内求解的问题。

例如，图的旅行商问题（TSP）和布尔可满足性问题（SAT）等问题被认为是难解问题。

难解问题的求解需要指数级的时间或空间复杂度，因此在实际中很难找到有效的算法。

2.3复杂度类别：计算复杂性理论还研究了不同问题的复杂度类别。

《计算理论》复习题总结1、自动机、可计算性、复杂性内涵及关系；计算理论的三个传统的核心领域：自动机、可计算性和复杂性。

通过“计算机的基本能力和局限性是什么？“这一问题将这三个领域联系在一起。

可计算理论与复杂性理论是密切相关的，在复杂性理论中，目标是把问题分成容易计算的和难计算的；而在可计算理论中，是把问题分成可解的和不可解。

自动机阐述了计算的数学模型的定义和性质，主要包含两种模型：有穷自动机模型；上下文无关文法模型。

可计算性理论和复杂性理论需要对计算机给了一个准确的定义。

自动机理论允许在介绍与计算机科学的其他非理论领域有关的概念时使用计算的形式化定义。

2、有穷自动机、正则语言、正则表达式、非确定有穷自动机、非正则语言；有穷自动机：描述能力和资源极其有限的计算机模型。

是一个5元组（Q，∑，δ，q0,F），其中1）Q是一个有穷集合，称为状态集。

2）∑是一个有穷集合，称为字母表。

3）δ：Q×∑→Q是转移函数。

4）q0∈Q是起始状态。

5）F⊆Q是接受状态集。

正则语言：如果一个语言能被有穷自动机识别。

正则表达式：用正则运算符构造描述语言的表达式。

称R是正则表达式，如果R是：1）a，a是字母表中的一个元素；2）ε；3）∅;4）（R1⋃R2）；5）(R1 R2)；6）(R1*)非确定有穷自动机：是一个5元组（Q，∑，δ，q0,F），其中1）Q是有穷状态集。

2）∑是有穷字母表。

3）δ：Q×∑ε→P（Q）是转移函数。

4）q0∈Q是起始状态。

5）F⊆Q是接受状态集。

3、上下文无关语言及上下文无关文法、歧义性、乔姆斯基范式、下推自动机、等价性、非上下文无关语言；上下文无关语言：用上下文无关文法生成的语言。

上下文无关文法：是一个4元组（V，∑，R，S）且1）V是一个有穷集合，称为变元集2）∑是一个与V不相交的有穷集合，称为终结符集3）R是一个有穷规则集，每条规则由一个变元和一个由变元及终结符组成的字符串构成，4）S∈V是起始变元歧义性：如果字符串W在上下文无关文法G中有两个或者两上以上不同的最左派生，则称G歧义地产生的字符串W。

计算理论基础知识计算理论是计算机科学的核心领域之一，它研究的是计算过程的本质和限制。

在计算机科学的发展过程中，计算理论提供了重要的理论基础和方法，为计算机科学和技术的发展奠定了坚实的基础。

本文将简要介绍计算理论的基础知识。

一、自动机理论自动机是计算理论中的重要概念之一，它用于描述计算过程的抽象模型。

自动机可以分为有限自动机和非确定性有限自动机等多种类型。

有限自动机是一种最简单的计算模型，它由状态、输入字母表、转换函数和初始状态等组成。

通过状态的转换和输入的驱动，有限自动机可以执行特定的计算任务。

非确定性有限自动机则相对更加复杂，它在进行状态转换时可以有多个可能的选项。

二、形式语言与文法形式语言和文法是计算理论中研究自动机行为规律的重要工具。

形式语言是由符号组成的集合，用于表示计算过程中的输入、输出和中间结果等信息。

文法则定义了形式语言的句子生成规则。

常见的文法类型有上下文无关文法、上下文相关文法等。

形式语言和文法的研究使得我们能够通过规则来描述和分析计算过程，从而更好地理解计算机科学中的一些重要概念和问题。

三、图灵机和可计算性理论图灵机是计算理论中最重要的概念之一，它由一个无限长的纸带和一个读写头组成。

图灵机通过读写头在纸带上的移动和改写来模拟计算过程。

图灵机的提出使得我们能够更深入地研究计算过程的本质和限制。

可计算性理论是计算理论中的一个重要分支，它研究的是什么样的问题可以通过某种计算模型解决。

根据可计算性理论，存在一些问题是不可计算的，即无法用任何计算模型来解决。

四、复杂性理论复杂性理论是计算理论中的另一个重要分支，它研究的是计算问题的复杂度。

复杂性理论主要关注计算问题的难解性和可解性。

常见的复杂性类别有P类、NP类等。

P类问题是可以在多项式时间内解决的问题，而NP类问题是可以在多项式时间内验证解的问题。

复杂性理论的研究使得我们能够更好地理解计算问题的本质，从而设计更高效的算法和方法。

五、计算复杂性和可计算性的关系计算复杂性和可计算性是计算理论中两个重要的概念。

复杂度理论是数学中的一个重要分支，研究的是计算问题的复杂性。

它旨在回答一个关键问题：对于一个给定的问题，我们在有限时间内能否找到一个解决方案，并且这个解决方案需要多长的时间。

复杂度理论的研究对象是算法，它描述了在解决问题时所需要的计算资源的需求。

在复杂度理论中，有两个重要的概念：时间复杂度和空间复杂度。

时间复杂度表示在解决问题时所需要的时间资源，通常用“大O符号”来表示。

例如，如果一个算法的时间复杂度是O(n^2)，说明算法的执行时间与输入数据的规模n的平方成正比，即随着n的增大，算法的执行时间也会增加。

另一方面，空间复杂度描述的是算法在解决问题时所需要的额外空间的需求，同样用“大O符号”来表示。

复杂度理论的研究对于计算机科学和其他领域的研究具有重要的意义。

它可以帮助人们评估算法的效率，从而选择最合适的算法来解决问题。

通过研究不同算法的复杂度，人们可以发现对于某些问题，可能不存在一个高效的算法来解决，从而引发了一些著名的计算难题，如NP完全问题和P=NP问题。

以NP完全问题为例，它是一类算法的集合，这些算法在给定一个解的情况下，可以在多项式时间内验证这个解的正确性。

然而，至今没有人找到一个高效的算法来解决NP完全问题，这就引发了一个重要的问题：P=NP问题。

如果P=NP成立，意味着可以在多项式时间内找到NP问题的解决方案，这将在计算理论和实践中引发重大的变革。

除了NP完全问题，复杂度理论还研究了其他一些重要的问题，如图论中的旅行商问题和图染色问题，及博弈论中的囚徒困境和社交网络中的影响力最大化问题等。

通过研究这些问题的复杂度，我们可以更深入地了解这些问题的难度，为问题的解决方案提供指导。

总之，数学中的复杂度理论是一门重要的研究领域，它研究的是计算问题的复杂性。

通过研究问题的复杂度，我们可以评估算法的效率，发现和解决一些重要的计算难题，并为问题的解决方案提供指导。

复杂度理论的研究对于计算科学和其他领域的研究具有重要的意义，帮助我们更深入地理解计算问题的本质。

理论计算机科学中的计算复杂性理论研究毕业论文Abstract:计算复杂性理论是理论计算机科学中的一个重要研究领域。

本文从该领域的起源、基本概念和主要研究内容三个方面探讨计算复杂性理论的重要性及其在实际应用中的作用。

首先介绍了计算复杂性理论的起源和发展历程，接着解释了计算问题、计算模型、算法和复杂性的基本概念。

随后探讨了计算复杂性理论在计算机科学中的核心问题，包括P与NP问题、NP完全性和NP难度、多项式时间可解问题等。

最后，讨论了计算复杂性理论在实际应用中的作用和价值，并对其未来发展进行了展望。

1. 引言计算复杂性理论是理论计算机科学中的一个重要研究领域，是研究计算机算法和问题的困难程度的理论基础。

自20世纪60年代以来，计算复杂性理论逐渐发展成为理论计算机科学的基石之一。

计算复杂性理论的研究成果不仅为计算机科学的发展提供了理论依据，也为解决实际问题提供了方法和策略。

2. 计算复杂性理论的起源与发展计算复杂性理论的起源可以追溯到20世纪50年代末和60年代初，其最早的研究动机源于对计算问题的困难性的认识。

此后，随着计算机技术的快速发展，计算复杂性理论逐渐形成并得到广泛应用。

计算复杂性理论的发展受益于图灵机模型、多项式时间可解、NP完全性等基本概念的提出和研究。

3. 计算问题的基本概念与模型在计算复杂性理论中，计算问题是研究的基本对象。

计算问题可以通过算法解决，而算法又可以由计算模型来描述。

计算模型是一个形式化的数学模型，用于描述计算过程中使用的有限资源和约束条件。

计算问题的本质是找到一种有效的算法来解决它，而算法的复杂度则是刻画算法的时间和空间资源使用情况的度量。

4. 计算复杂性理论的核心问题计算复杂性理论的核心问题之一是P与NP问题。

P和NP是两个重要的复杂性类，前者表示在多项式时间内可解的问题，后者表示在非确定性多项式时间内可解的问题。

P与NP问题的解答关系到计算理论的基础性问题。

另一个核心问题是NP完全性和NP难度的研究，它们是复杂性理论中的重要概念。

《计算理论》计算理论计算理论是计算机科学的一个重要分支，它研究计算的本质、计算机的局限性、算法的复杂性等问题。

计算理论不仅对计算机科学的理论研究有着重要的贡献，而且对计算机科学的实际应用也有着重要的指导意义。

本文将从计算理论的基础概念、重要方法和应用研究方面分别进行综述。

一、计算理论的基础概念计算理论的基础概念包括自动机、图灵机、可计算性、复杂性等。

1.自动机自动机是一种数学模型，描述一组有限状态与转换规则，它可以接受或拒绝输入的序列。

其种类包括有限自动机、下推自动机、图灵机等，其中图灵机是计算理论中最重要的一种自动机。

2.图灵机图灵机是由英国数学家图灵（Alan Turing）在1936年提出的，它是一种虚拟机器，可以模拟任何其他计算模型的算法，其所能解决的问题可以称之为可计算问题。

图灵机包括状态寄存器、可写磁带、读写头等组成部分，它可以读取磁带上的输入符号，根据规则执行计算，并将结果输出到磁带上。

3.可计算性可计算性是计算理论中的一个基本概念，它指的是能够通过某种计算模型进行计算的问题。

如果一个问题可以被图灵机计算，那么它就具有可计算性。

4.复杂性复杂性是计算理论中的另一个核心概念，它指的是计算的时间和空间复杂度。

时间复杂度指的是算法执行所需的时间，而空间复杂度指的是算法执行所需的空间。

通常通过渐进符号来表示算法的复杂性，如O(n)、O(nlogn)等。

二、计算理论的重要方法计算理论的重要方法包括可计算性理论、复杂性理论、自动机理论等。

1.可计算性理论可计算性理论是研究问题的可计算性的理论。

该理论主要使用图灵机等计算模型来描述问题的可计算性，其重要结论包括：（1）停机问题不可解停机问题是指给定一个程序及其输入，是否可以在有限时间内停止运行。

停机问题不可解意味着不存在一个通用算法，可以判定任意程序是否会在有限时间内停机。

（2）哥德尔不完备定理哥德尔不完备定理指的是，任何形式化的公理化系统都存在某些命题是无法通过该系统来证明的。

计算科学知识点总结计算科学是一个跨学科领域，涉及计算和数学、物理、统计学、工程等多个学科的知识。

它是对问题建模、算法设计和计算机实现的交叉研究。

计算科学的发展旨在解决现实世界中的复杂问题，包括计算机科学、数学建模、仿真、数据分析、人工智能等方面。

本文将对计算科学中的一些重要知识点做一个总结。

1. 计算模型与理论计算模型是计算科学的基础，它是对计算机行为的数学抽象。

常用的计算模型包括图灵机、有限状态自动机、递归函数等。

理论计算机科学研究的内容包括计算理论、自动机理论、算法理论等，它们探讨计算机能力和限制、计算问题的可解性和难解性。

2. 算法分析与设计算法是解决问题的一组有序操作，算法分析与设计研究如何设计高效和正确的算法。

常见的算法设计技巧包括贪心算法、分治算法、动态规划算法、回溯算法等。

算法的性能评估包括时间复杂度和空间复杂度分析、算法正确性和稳定性分析、算法优化等。

3. 数据结构数据结构是组织和存储数据的方式，常用的数据结构包括数组、链表、栈、队列、树、图等。

数据结构的选择和设计影响算法的性能和实现。

在计算科学中，数据结构的研究和应用涉及到存储、检索、排序、搜索、遍历等操作。

4. 计算机体系结构与操作系统计算机体系结构研究计算机硬件和软件的交互关系，包括处理器、存储器、输入输出设备等组件的设计和实现。

操作系统是计算机系统的核心软件，负责管理计算资源、提供用户接口和服务。

计算机体系结构与操作系统的研究包括计算机组成原理、操作系统原理、嵌入式系统等。

5. 编程语言与编程范式编程语言是计算机与人沟通的桥梁，常用的编程语言包括C、C++、Java、Python、JavaScript等。

编程语言的设计哲学和编程范式影响程序设计的风格和实现方法。

常见的编程范式包括过程化编程、面向对象编程、函数式编程、逻辑编程等。

6. 数值计算与科学计算数值计算是使用数值方法求解数学问题的研究领域，它包括线性代数、微分方程、积分方程、最优化等。