相似三角形判定复习(一)

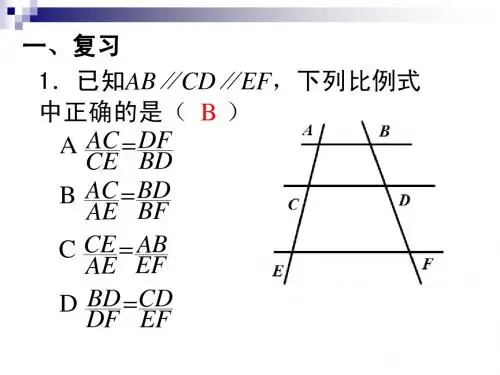
2023年九年级数学下册第27章《相似》复习检测卷（一）考试范围：§27.1图形的相似~27.2相似三角形的判定满分：120分一、选择题(每小题3分，共30分)1.将△ABC 的每条边都扩大3倍得到△DEF ，其中点A 、B 、C 的对应点分别是D 、E 、F ，则∠D 与∠A 的关系为（）A .∠D ＝∠AB .∠D ＝3∠AC .∠D ＝6∠AD .∠D ＝9∠A2.如图，在△ABC 中，∠A ＝78°，AB ＝4，AC ＝6，将△ABC 沿图中的虚线剪开，剪下的阴影三角形与原三角形不相似的是（）3.如图，已知直线a ∥b ∥c ，直线m 、n 与a 、b 、c 分别交于点A 、C 、E ，B 、D 、F ，AC ＝8，CE ＝12，BD ＝6，则DF 的长为（）A .4B .5C .9D .74.如图，在△ABC 中，D 、E 分别为AB 、AC 边上的点，DE ∥BC ，F 为BC 边上一点，连接AF交DE 于点G ，则下列结论中一定正确的是（）A .AD AEAB CE=B .AC AEGF BD=C .BD CEAD AE=D .AG ACAF CE=5.如图，在正方形网格上有两个三角形，且△ABC 和△DEF 相似，则∠BAC 的度数为（）A .135°B .125°C .115°D .105°6.如图，△ACP ∽△ABC ，若∠A ＝100°，∠ACP ＝20°，则∠ACB 的度数是（）A .80°B .60°C .50°D .30°7.如图，在□ABCD 中，EF ∥AB ，DE ∶EA ＝2∶3，EF ＝4，则CD 的长为（）A .6B .8C .9D .108.要制作两个形状相同的三角形框架，其中一个三角形的三边长分别为5cm 、6cm 和9cm ，另一个三角形的最短边长为2.5cm ，则它的最长边为（）A .3cmB .4cmC .4.5cmD .5cm9.如图，在矩形ABCD 中，AB ＝a ，AD ＝3，按照图中的方式将它分成完全相同的三个矩形，如果每一个小矩形都与矩形ABCD 相似，则a 的值为（）第5题第3题第4题第6题第7题第9题第10题A .22B .23C .33D .3210.如图，正方形ABCD 的边长为4，E 是BC 边上一点，过点E 作EF ⊥AE 交CD 边于点F ，则CF 的最大值是（）A .0.5B .1C .1.5D .2二、填空题(每小题3分，共18分)11.如图，添加一个条件__________________，使△ADE ∽△ACB .12.如图，在□ABCD 中，E 是AD 的中点，EC 交对角线BD 于点F ，则BF ∶FD 的值为_________.13.如图，在△ABC 中，DE ∥BC ，若AD ＝1，BD ＝3，BC ＝8，则DE 的长为________.14.已知654a b c==，且a ＋b －2c ＝6，则a 的值为_______.15.如图，在Rt △OAC 中，O 为坐标原点，直角顶点C 在x 轴的正半轴上，反比例函数ky x=(k ＞0)在第一象限的图象经过OA 的中点B ，交AC 于点D ，连接OD ，若△OCD ∽△ACO ，则直线OA 的解析式为_______.16.如图，直线l 1∥l 2∥l 3，直线l 1与l 2之间的距离为2，直线l 2与l 3之间的距离为1，等边△ABC 的三个顶点分别在直线l 1、l 2、l 3上，则等边三角形的边长是______.三、解答题(共8题，共72分)17.(8分)如图，四边形ABCD ∽四边形A 'B 'C 'D '，∠BCD ＝125°，分别求x 、y 、α的值.18.(8分)如图，在矩形ABCD 中，点E 、F 分别在BC 、CD 上，AE ⊥BF 于点M ，若BC ＝2AB ，探究AE 与BF 的数量关系，并证明你的结论.第10题第11题第16题第12题第13题第15题19.(8分)如图，在四边形ABCD中，AC平分∠BAD，∠ADC＝∠ACB＝90°.(1)求证：AC2＝AB·AD；(2)若BC＝3，AB＝5，求CD的长.20.(8分)如图，在矩形ABCD中，E是AD上一点，连接BE.(1)请用尺规在BE上求作一点P，使得△PCB∽△ABE(不写作法，保留作图痕迹)；(2)若AE＝3，AB＝4，BC＝6，求EP的长.21.(8分)如图，在△ABC中，AB＝2，BC＝4，D为BC边上一点，BD＝1.(1)求证：△ABD∽△CBA；(2)作DE∥AB交AC于点E，请直接写出另一个与△ABD相似的三角形，并求出DE的长.22.(10分)在△ABC中，AB＝6，AC＝8，点D、E分别在AB、AC上，连接DE，设BD＝x(0＜x＜6)，CE＝y(0＜y＜8).(1)当x＝2，y＝5时，求证：△AED∽△ABC；(2)若△ADE和△ABC相似，求y与x的函数表达式.23.(10分)如图，在△ABC中，∠ABC＝90°，D是斜边AC的中点，连接DB.过点A作AE⊥BD于点F，交BC于点E.(1)求证：EB2＝EF・EA；(2)若AB＝4，CE＝3BE，求AE的长.24.(12分)(1)【问题背景】如图1，D是等边△ABC中AB边上的点，以CD为边在CD的上方作等边△CDE，连接AE，求证：BD＝AE；(2)【尝试应用】如图2，D是Rt△ABC中AB边上的一点，∠B＝90°，∠BAC＝30°，以CD为边在CD的上方作Rt△CDE，使∠CDE＝90°，∠CED＝30°，连接AE，请探究BD与AE的数量关系，并说明理由；(3)【拓展创新】如图3，在Rt△ABC中，∠ABC＝90°，点D在AB边上，以CD为边在CD的上方作Rt△CDE，使∠CDE＝90°，43DE ABCD BC==，DE交AC于F，若AD＝3BD，求AFDF的值.《相似》阶段检测卷(一)考试范围：§27.1图形的相似~27.2相似三角形的判定满分：120分一、选择题(每小题3分，共30分)1.将△ABC 的每条边都扩大3倍得到△DEF ，其中点A 、B 、C 的对应点分别是D 、E 、F ，则∠D 与∠A 的关系为（）A .∠D ＝∠AB .∠D ＝3∠AC .∠D ＝6∠A D .∠D ＝9∠A【答案】A .详解：依题意，△ABC 与△DEF 的三边成比例，∴△ABC ∽△DEF ，∴∠A ＝∠D ，故选A .2.如图，在△ABC 中，∠A ＝78°，AB ＝4，AC ＝6，将△ABC 沿图中的虚线剪开，剪下的阴影三角形与原三角形不相似的是（）【答案】C .详解：由两个角分别相等的两个三角形相似，知选项A 和B 中的阴影三角形与原三角形相似，选项D 中，阴影三角形的∠A 的两边分别为4－1＝3，6－4＝2，∵4623=，∠A ＝∠A ，∴选项D 中的阴影三角形与原三角形相似.而选项C 中，不能保证∠B 的两边成比例，故选C .3.如图，已知直线a ∥b ∥c ，直线m 、n 与a 、b 、c 分别交于点A 、C 、E ，B 、D 、F ，AC ＝8，CE ＝12，BD ＝6，则DF 的长为（）A .4B .5C .9D .7【答案】C .详解：∵a ∥b ∥c ，∴AC BD CE DF =，即8612DF=，解得DF ＝9，故选C . 4.如图，在△ABC 中，D 、E 分别为AB 、AC 边上的点，DE ∥BC ，F 为BC 边上一点，连接AF 交DE 于点G ，则下列结论中一定正确的是（）A .AD AEAB CE=B .AC AEGF BD=C .BD CEAD AE=D .AG ACAF CE=【答案】C .详解：∵DE ∥BC ，∴BD CE AD AE =，故C 对；AD AEAB AC=，故A 错；AG AE ADAF AC AB==，故D 错；选项B 中的4条线段不成比例，故D 错.故选C .5.如图，在正方形网格上有两个三角形，且△ABC 和△DEF 相似，则∠BAC 的度数为（）A .135°B .125°C .115°D .105°【答案】A .详解：∵△ABC 和△DEF 相似，观察角的大小，∠BAC ＝∠DEF ＝90°＋45°＝135°，故选A . 6.如图，△ACP ∽△ABC ，若∠A ＝100°，∠ACP ＝20°，则∠ACB 的度数是（）A .80°B .60°C .50°D .30°【答案】B .详解：在△ACP 中，∵∠A ＝100°，∠ACP ＝20°，∴∠APC ＝60°.∵△ACP ∽△ABC ，∴∠ACB ＝∠APC ＝60°，故选B .7.如图，在□ABCD 中，EF ∥AB ，DE ∶EA ＝2∶3，EF ＝4，则CD 的长为（）A .6B .8C .9D .10【答案】D .详解：∵EF ∥AB ，∴EF DEAB DA=，∵DE ∶EA ＝2∶3，EF ＝4，∴4223AB =+，∴AB ＝10，则CD ＝AB ＝10，故选D .8.要制作两个形状相同的三角形框架，其中一个三角形的三边长分别为5cm 、6cm 和9cm ，另一个三角形的最短边长为2.5cm ，则它的最长边为（）A .3cmB .4cmC .4.5cmD .5cm【答案】C .详解：设所求的最长边为xcm ，则592.5x=，解得x ＝4.5，故选C .9.如图，在矩形ABCD 中，AB ＝a ，AD ＝3，按照图中的方式将它分成完全相同的三个矩形，如果每一个小矩形都与矩形ABCD 相似，则a 的值为（）A .B .C .D .【答案】C .详解：小矩形的边边分别为13a 和3，∵小矩形与矩形ABCD 相似，∴13a ∶3＝3∶a ，解得a ＝±(舍去负值)，∴a ＝C .10.如图，正方形ABCD 的边长为4，E 是BC 边上一点，过点E 作EF ⊥AE交CD 边于点F ，则CF 的最大值是（）A .0.5B .1C .1.5D .2【答案】B .详解：∵∠B ＝∠C ＝90°，AE ⊥EF ，可证△ABE ∽△ECF ，∴AB BECE CF=，设BE ＝x ，则CE ＝4－x ，∴44x x CF =-，∴CF ＝14x (4－x )＝－14(x －2)2＋1，当x ＝2时，CF 取得最大值1，故选B .二、填空题(每小题3分，共18分)11.如图，添加一个条件__________________，使△ADE ∽△ACB .【答案】答案不唯一，可以填下列中的一个：∠ADE ＝∠C ，∠AED ＝∠B ，AD AEAC AB=.12.如图，在□ABCD 中，E 是AD 的中点，EC 交对角线BD 于点F ，则BF ∶FD的值为_________.【答案】2.详解：∵四边形ABCD 为平行四边形，∴BC ＝AD ，BC ∥AD .∵E 为AD 的中点，∴BC ＝AD ＝2DE ，由AD ∥BC ，得△BCF ∽DEF ，∴BF ∶FD ＝BC ∶DE ＝2.13.如图，在△ABC 中，DE ∥BC ，若AD ＝1，BD ＝3，BC ＝8，则DE 的长为________.【答案】2.详解：∵DE ∥BC ，∴AD DE AB BC =，即1138DE=+，∴DE ＝2.14.已知654a b c==，且a ＋b －2c ＝6，则a 的值为_______.【答案】12.详解：∵654a b c==，故可设a ＝6x ，b ＝5x ，c ＝4x ，代入a ＋b －2c ＝6，得：6x ＋5x －2(4x )＝6，解得x ＝2，∴a ＝6x ＝12.15.如图，在Rt △OAC 中，O 为坐标原点，直角顶点C 在x 轴的正半轴上，反比例函数ky x=(k ＞0)在第一象限的图象经过OA 的中点B ，交AC 于点D ，连接OD ，若△OCD ∽△ACO ，则直线OA 的解析式为_______.【答案】y ＝2x .详解：设B (t ，k t )，则直线OA 的解析式为y ＝2ktx .∵B 为OA 的中点，∴A (2t ，2k t )，∴D (2t ，2k t )，OC ＝2t ，CD ＝2k t ，CA ＝2kt.∵△OCD ∽△ACO ，∴OC CD AC OC =，∴OC 2＝AC ·CD ，∴4t 2＝2k t ·2k t，∴k 2＝4t 4，∵k ＞0，∴k ＝2t 2，∴直线OA 的解析式为y ＝2x .16.如图，直线l 1∥l 2∥l 3，直线l 1与l 2之间的距离为2，直线l 2与l 3之间的距离为1，等边△ABC 的三个顶点分别在直线l 1、l 2、l 3上，则等边三角形的边长是______.【答案】2213.F详解：过C 作CE ⊥AC 交AB 的延长线于D ，过C 作CF ⊥l 1于F ，交l 3于H ，过E 作ED ⊥FC 交延长线于D ，∵∠AFC ＝∠ACE＝∠CDE ＝90°，∴△ACF ∽△CED ，∴DE CD CECF AF AC==，∵△ABC 为等边△，∴CE ，AB ＝BC ＝BE ，则CD AF .依题意，FH ＝FC ＋CH ＝2＋1＝3，由AB ＝BE ，l 1∥l 3∥ED ，得DH ＝FH ＝3，CD ＝4，∴AF CD AC .三、解答题(共8题，共72分)17.(8分)如图，四边形ABCD ∽四边形A 'B 'C 'D '，∠BCD ＝125°，分别求x 、y 、α的值.【答案】∵四边形ABCD ∽四边形A 'B 'C 'D '，∴∠C ′＝∠C ＝125°，∴∠α＝360°－80°－75°－125°＝80°，且AD AB BC A D A B B C ==''''''，即45316x y==，解得x ＝20，y ＝12.答：x ＝20，y ＝12，α＝80°.18.(8分)如图，在矩形ABCD 中，点E 、F 分别在BC 、CD 上，AE ⊥BF 于点M ，若BC ，探究AE 与BF 的数量关系，并证明你的结论.【答案】BF AE ，理由如下：∵四边形ABCD 是矩形，∴∠ABC ＝∠C ，∵AE ⊥BF ，∴∠AMB ＝∠BAM ＋∠ABM ＝90°，又∵∠ABM ＋∠CBF ＝90°，∴∠BAM ＝∠CBF ，∴△ABE ∽△BCF ，∴AE AB BF BC ==，∴BF AE .19.(8分)如图，在四边形ABCD 中，AC 平分∠BAD ，∠ADC ＝∠ACB ＝90°.(1)求证：AC 2＝AB ·AD ；(2)若BC ＝3，AB ＝5，求CD 的长.【答案】(1)∵AC 平分∠BAD ，∴∠DAC ＝∠CAB .∵∠ADC ＝∠ACB ＝90°，∴△ADC ∽△ACB ，∴AD ACAC AB=，∴AC 2＝AB ·AD .(2)在Rt △ABC 中，∵BC ＝3，AB ＝5，由勾股定理，得AC ＝4.∵AC 2＝AB ·AD ，∴42＝5AD ，∴AD ＝165.在Rt △ADC 中，CD 125.20.(8分)如图，在矩形ABCD 中，E 是AD 上一点，连接BE .(1)请用尺规在BE 上求作一点P ，使得△PCB ∽△ABE(不写作法，保留作图痕迹)；(2)若AE ＝3，AB ＝4，BC ＝6，求EP 的长.【答案】(1)如图所示；(2)由勾股定理，得BE 5，由△PCB ∽△ABE ，得BP BC AE BE =，即635BP =，∴BP ＝185，∴EP ＝BE －BP ＝5－185＝75.21.(8分)如图，在△ABC 中，AB ＝2，BC ＝4，D 为BC 边上一点，BD ＝1.(1)求证：△ABD ∽△CBA ；(2)作DE ∥AB 交AC 于点E ，请直接写出另一个与△ABD 相似的三角形，并求出DE 的长.【答案】(1)∵AB ＝2，BC ＝4，BD ＝1，∴AB BDBC AB=，又∠ABD ＝∠CBA ，∴△ABD ∽△CBA .(2)如图，∵DE ∥AB ，∴△CDE ∽△CBA ，∵△ABD ∽△CBA ，∴△CDE ∽△ABD ，∴DE CD BD AB =，即4112DE -=，∴DE ＝1.5.22.(10分)在△ABC 中，AB ＝6，AC ＝8，点D 、E 分别在AB 、AC 上，连接DE ，设BD ＝x (0＜x ＜6)，CE ＝y (0＜y ＜8).(1)当x ＝2，y ＝5时，求证：△AED ∽△ABC ；(2)若△ADE 和△ABC 相似，求y 与x 的函数表达式.【答案】(1)∵AB ＝6，BD ＝x ＝2，∴AD ＝4.∵AC ＝8，CE ＝y ＝5，∴AE ＝3.∴AD AEAC AB=.又∵∠EAD ＝∠BAC ，∴△AED ∽△ABC .(2)分两种情况，1°当△ADE ∽△ABC 时，AD AE AB AC =，则6868x y --=，∴y ＝43x (0＜x ＜6).2°当△ADE ∽△ACB 时，AD AE AC AB =，则6886x y --=，∴y ＝34x ＋72(0＜x ＜6).23.(10分)如图，在△ABC 中，∠ABC ＝90°，D 是斜边AC 的中点，连接DB .过点A 作AE ⊥BD 于点F ，交BC 于点E .(1)求证：EB 2＝EF ・EA ；(2)若AB ＝4，CE ＝3BE ，求AE 的长.【答案】(1)∵AE ⊥BD ，∴∠BFE ＝90°＝∠ABC .又∵∠BEF ＝∠AEB ，∴△EBF ∽△EAB ，∴BE EFAE BE=，∴EB 2＝EF ・EA .(2)在Rt △ABC 中，∵D 为斜边AC 的中点，∴BD ＝CD ，∴∠DBC ＝∠C .由(1)，得△EBF∽△EAB，∴∠EBF＝∠EAB，∴∠C＝∠EAB.又∠ABE＝∠CBA，∴△BAE∽△BCA，∴AB BEBC AB=，∴AB2＝BE·BC.∵AB＝4，CE＝3BE，∴BC＝4BE，42＝BE(4BE)，∴BE＝2.∴AE＝.24.(12分)(1)【问题背景】如图1，D是等边△ABC中AB边上的点，以CD为边在CD的上方作等边△CDE，连接AE，求证：BD＝AE；(2)【尝试应用】如图2，D是Rt△ABC中AB边上的一点，∠B＝90°，∠BAC＝30°，以CD为边在CD的上方作Rt△CDE，使∠CDE＝90°，∠CED＝30°，连接AE，请探究BD与AE的数量关系，并说明理由；(3)【拓展创新】如图3，在Rt△ABC中，∠ABC＝90°，点D在AB边上，以CD为边在CD的上方作Rt△CDE，使∠CDE＝90°，43DE ABCD BC==，DE交AC于F，若AD＝3BD，求AFDF的值.【答案】(1)∵△ABC与△CDE均为等边三角形，∴BC＝AC，CD＝CE，∠ACB＝∠DCE＝60°，∴∠BCD＝∠ACE，∴△BCD≌△ACE，∴BD＝AE.(2)AE＝2BD，理由如下：∵∠BAC＝∠DEC＝30°，∠B＝∠EDC＝90°，∴△ABC∽△EDC，∴BC AC CD CE=.由条件得∠ACB＝∠DCE，AC＝2BC，∴∠BCD＝∠ACE，∴△BCD∽△ACE，∴12BD BCAE AC==，∴AE＝2BD.(3)由(2)得，△BCD∽△ACE，∴AE ACBD BC=，∵43DE ABCD BC==，∴53ACBC=，∴53AE ACBD BC==设BD＝a，则AD＝3BD＝3a，AB＝4a，BC＝3a，CDa，AE＝53BD＝53a.∵△AFE∽△DFC ，∴53aAF AEDF CD=.。