工程力学(静力学与材料力学)-10-组合受力与变形杆件的强度计算

工程力学（静力学与材料力学）习题第12章 失效分析与设计准则12－ 1 对于建立材料在一般应力状态下的失效判据与设计准则，试选择如下合适的论述。

（A ）逐一进行试验，确定极限应力；（B ）无需进行试验，只需关于失效原因的假说；（C ）需要进行某些试验，无需关于失效原因的假说； （D ）假设失效的共同原因，根据简单试验结果。

正确答案是 。

12－2 对于图示的应力状态（y x σσ>）若为脆性材料，试分析失效可能发生在：（A ）平行于x 轴的平面； （B ）平行于z 轴的平面；（C ）平行于Oyz 坐标面的平面； （D ）平行于Oxy 坐标面的平面。

正确答案是 。

12－3 对于图示的应力状态，若x y σσ=，且为韧性材料，试根据最大切应力准则，失效可能发生在：（A ）平行于y 轴、其法线与x 轴的夹角为45°的平面，或平行于x 轴、其法线与y 轴的夹角为45°的平面内；（B ）仅为平行于y 轴、法线与z 轴的夹角为45°的平面； （C ）仅为平行于z 轴、其法线与x 轴的夹角为45°的平面； （D ）仅为平行于x 轴、其法线与y 轴的夹角为45°的平面。

正确答案是 。

12－4 铸铁处于图示应力状态下，试分析最容易失效的是：（A ）仅图c ；（B ）图a 和图b ； （C ）图a 、b 和图c ； （D ）图a 、b 、c 和图d 。

正确答案是 。

12－5低碳钢处于图示应力状态下，若根据最大切应力准则，试分析最容易失效的是： （A ）仅图d ； （B ）仅图c ； （C ）图c 和图d ； （D ）图a 、b 和图d 。

正确答案是 。

12－6 韧性材料所处应力状态如图所示，根据最大切应力准则，试分析二者同时失效的条件是： （A ）τσ>，3/2στ=； （B ）τσ<，3/4στ=； （C ）τσ=；（D ）τσ>，3/2τσ=。

工程力学考试答卷（10）1．（5分）结构对称的梁在反对称载荷作用下：弯矩图对称，剪力图反对称；弯矩图反对称，剪力图对称；弯矩图和剪力图都对称；弯矩图和剪力图都反对称。

正确答案是B。

2．（5分）关于材料的力学一般性能，有如下结论，请判断哪一个是正确的：脆性材料的抗拉能力低于其抗压能力；（B）脆性材料的抗拉能力高于其抗压能力；（C）韧性材料的抗拉能力高于其抗压能力；正确答案是A。

（D）脆性材料的抗拉能力等于其抗压能力。

3．（5分）关于斜弯曲的主要特征有以下四种答案，请判断哪一种是正确的。

（A） My≠0，Mz≠0，FNx≠0；，中性轴与截面形心主轴不一致，且不通过截面形心；（B） My≠0，Mz≠0，FNx＝0，中性轴与截面形心主轴不一致，但通过截面形心；（C） My≠0，Mz≠0，FNx＝0，中性轴与截面形心主轴平行，但不通过截面形心；（D） My≠0，Mz≠0，FNx≠0，中性轴与截面形心主轴平行，但不通过截面形心。

正确答案是B。

4．（5分）两根长度相等、直径不等的圆轴受扭后，轴表面上母线转过相同的角度。

设直径大的轴和直径小的轴的横截面上的最大剪应力分别为τ1max和τ2max，材料的切变模量分别为G1和G2。

关于τ1max和τ2max的大小，有下列四种结论，请判断哪一种是正确的。

（A）τ1max>τ2max；（B）τ1max<τ2max；（C）若G1>G2，则有τ1max>τ2max；正确答案是C。

（D）若G1>G2，则有τ1max<τ2max。

5．（10分）截面为工字形的立柱受力如图所示。

试求此力向截面形心C平移的结果。

解：r =（-50, 125, 0）mm F =（0, 0, -100）kN F 向C 平移，得 FR =（0, 0, -100）kN1000000.1250.05-)(-=⨯==kj i F r F M M C C=（-12.5, -5, 0）kN ·m6．（10分）图示芯轴AB 与轴套CD 的轴线重合，二者在B 、C 处连成一体；在D 处无接触。

习题13-4图 工程力学（静力学与材料力学）习题第13章 杆类构件的静力学设计13－1 关于低碳钢试样拉伸至屈服时，有如下结论：（A ）应力和塑性变形很快增加，因而认为材料失效；（B ）应力和塑性变形虽然很快增加，但不意味着材料失效；（C ）应力不增加塑性变形很快增加，因而认为材料失效；（D ）应力不增加塑性变形很快增加，但不意味着材料失效。

正确答案是 。

13－2 韧性材料应变硬化之后，材料的力学性能发生下列变化：（A ）屈服应力提高，弹性模量降低；（B ）屈服应力提高，韧性降低；（C ）屈服应力不变，弹性模量不变；（D ）屈服应力不变，韧性不变。

正确答案是 。

13－3 关于条件屈服应力有如下论述：（A ）弹性应变为0.2%时的应力值；（B ）总应变为0.2%时的应力值；（C ）塑性应变为0.2%时的应力值；（D ）弹性应变为0.2时的应力值。

正确答案是 。

13－4 螺旋压紧装置如图所示。

现已知工作所受的压紧力为F = 4kN ，旋紧螺栓螺纹的内径d 1 = 13.8mm ，固定螺栓内径d 2 = 17.3mm 。

两根螺栓材料相同，其许用应力][σ= 53.0MPa 。

试校核各螺栓之强度是否安全。

13－5 现场施工中起重机吊环的每一侧臂AB 和BC ，均由两根矩形截面杆组成，连接处A 、B 、C 均为铰链，如图所示。

已知起重载荷F P = 1200kN ，每根矩形杆截面尺寸比例为b /h = 0.3，材料的许用应力][σ= 78.5MPa 。

试设计矩形杆的截面尺寸b 和h 。

13－6 图示结构中BC 和AC 都是圆截面直杆，直径均为d = 20mm ，材料都是Q235钢，其许用应力][σ= 157 MPa 。

试求该结构的许可载荷。

（有人说：根据垂直方面的平衡条件，有P N N 45cos 30cos F F F AC BC =︒+︒，然后将])[4/(2N σπd F BC =，])[4/(2N σπd F AC =代入后即可得许可载荷，这种解法对吗？为什么？）习题13-5图习题13-7图 习题13-8图 习题13-9图13－7 图示汽缸内径D = 560mm ，内压p = 2.5MPa，活塞杆直径d = 100mm ，所以用材料的屈服应力s σ= 300MPa 。

附件2：工程力学科目考试大纲一、考试性质工程力学是高等学校材料、石油、储运等诸多专业的重要技术基础课，也是相应专业硕士研究生入学考试科目之一。

工程力学考试是教育部授权各招生院校自行命题的选拔性考试，其目的是测试考生利用工程力学基础知识分析问题、解决问题的能力。

本大纲根据教育部高等工科本科理论力学课程（中学时）中静力学的要求和材料力学课程（中学时）基本要求及教育部工科力学课程教学指导委员会面向21世纪工科力学课程教学改革的要求，结合我校工科各专业对工程力学基本知识的要求而制订。

本大纲力求反映普通一般院校工科本科专业的特点，以科学、公平、准确、规范的尺度去测评考生的工程力学相关基础知识掌握水平，考生运用工程力学基础知识分析问题和解决问题的能力。

应考人员应根据本大纲的内容和要求自行组织学习相关内容和掌握有关知识。

二、评价目标(1) 要求考生具有较全面的关于工程力学的基础知识；(2) 要求考生具有一定的力学建模的能力；(3) 要求考生具有较高的分析问题和解决问题的能力；(4) 要求考生具有较强的综合知识运用能力。

三、考试内容（一）静力学1、静力学基础1）基本要求掌握力、力矩的基本概念及其性质，能熟练地计算力对点之矩和力对轴之矩；掌握力偶、力偶矩和力偶系的基本概念及其性质，能熟练地计算力偶矩；掌握力系主矢和主矩的基本概念及其性质，能熟练计算各类力系的主矢和主矩；理解和掌握力系等效定理和平衡力系定理；掌握各种常见约束及其约束力性质，能熟练画出单个刚体和刚体系的受力图。

2）考试内容1.1力的概念1.2力矩的概念1.3主矢和主矩1.4 力系等效定理和平衡力系定理1.5力偶和力偶矩矢1.6约束和约束力1.7 物体的受力分析及受力图2、力系简化1）基本要求掌握力系的简化方法和简化结果以及简化结果的相关应用；理解平行力系的中心，了解物体重心、质心和形心的确定方法，能熟练计算平面图形的形心。

2）考试内容2.1 一般力系简化结果2.2 固定端约束2.3 物体的重心、质心和形心2.4 平面图形的形心计算2.5 分布力的相关计算3、静力学平衡问题1）基本要求掌握各种力系的平衡条件和平衡方程，并能熟练地求解单个刚体和刚体系统的平衡问题；掌握桁架的概念及其理想化力学模型，掌握平面静定桁架内力计算；掌握滑动摩擦和摩擦角的概念，了解滚动摩阻的概念，能熟练地求解考虑滑动摩擦时的单个刚体和刚体系的平衡问题。

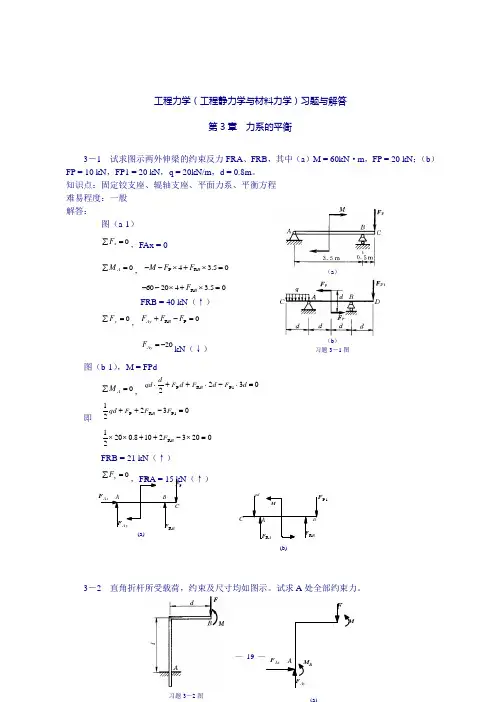
工程力学（工程静力学与材料力学）习题与解答第3章 力系的平衡3－1 试求图示两外伸梁的约束反力FRA 、FRB ，其中（a ）M = 60kN ·m ，FP = 20 kN ；（b ）FP = 10 kN ，FP1 = 20 kN ，q = 20kN/m ，d = 0.8m 。

知识点：固定铰支座、辊轴支座、平面力系、平衡方程 难易程度：一般 解答：图（a-1） 0=∑x F ，FAx = 00=∑A M ，05.34R P =⨯+⨯--B F F M 05.342060R =⨯+⨯--B F FRB = 40 kN （↑）=∑y F ，0P R =-+F F F B Ay20-=Ay F kN （↓）图（b-1），M = FPd 0=∑A M ，03221P R P =⋅-⋅++⋅d F d F d F dqd B即 032211P R P =-++F F F qd B 02032108.02021R =⨯-++⨯⨯B FFRB = 21 kN （↑）=∑y F ，FRA = 15 kN （↑）3－2 直角折杆所受载荷，约束及尺寸均如图示。

试求A 处全部约束力。

A MB Ay F B R F CAx F PF(a) M A B B R F A R F P 1F C qdBD(b)（a ）（b ） 习题3－1图FMB习题3－3图sF W A F ABF BF AN F(a)知识点：固定端约束、平面力系、平衡方程 难易程度：一般 解答： 图（a ）： 0=∑x F ，0=Ax F=∑y F ，=Ay F （↑）0=∑A M ，0=-+Fd M M AM Fd M A -=3－3 图示拖车重W = 20kN ，汽车对它的牵引力FS = 10 kN 。

试求拖车匀速直线行驶时，车轮A 、B 对地面的正压力。

知识点：固定端约束、平面力系、平衡方程 难易程度：一般解答： 图（a ）：0)(=∑F A M 08.214.1NB S =⨯+⨯-⨯-F F W6.13NB =F kN=∑y F ，4.6NA =F kN3－4 图示起重机ABC 具有铅垂转动轴AB ，起重机重W = 3.5kN ，重心在D 。

1、A03 B03 力的性质静力学基础2分三力平衡汇交定理是。

2、A01 B03 平衡方程静力学平衡2分如图所示系统在力F作用下处于平衡。

欲使A支座约束反力的作用线与AB 成30，则斜面的倾角α应为。

3、A03 B03 力偶的性质静力学基础2分两个力偶的等效条件是。

4、A02 B03 材料力学的基本假设材料力学的基本概念6分材料力学的基本假设有、和。

5、A02 B03 杆件应力拉（压）杆的应力2分轴向拉压杆件横截面上的正应力分布规律是沿方向，分布。

6、A01 B03 圆柱扭转时的切应力分析圆轴的扭转应力2分圆轴扭转时横截面上切应力的方向与垂直，轴表面各点均处于状态。

7、A03 B03 剪力与挤压的概念梁的内力分析4分对称弯曲梁的横截面上有和两种内力。

8、A01 B03 圆轴扭转时切应力梁的强度4分发生对称弯曲的矩形截面梁，最大剪力为max s F ，横截面面积为A ，则最大切应力max τ= ，最大切应力位于 。

9、A03 B03 切应力分析 圆轴的扭转应力 4分单元体上切应力等于零的平面称为 平面，此平面上的正应力称为应力。

10、A02 B03 杆的分析 压杆稳定性分析与设计 8分li μλ=称为压杆的 ，根据λ的大小，可将压杆分为 、和 三种类型。

11、A01 B03 力的简化 平面力系简化 4分在图示力系中，1234F =F =F =F F =，则力系向A 点的简化结果是 ，向B 点的简化结果是 。

12、A03 B03 力的三要素 静力学基础 8分力对物体的作用效应取决于力的三要素，即力的 、和 。

对于刚体而言，力是 矢量。

13、A03 B03 拉（压）杆件的应力 材料力学的基本概念 4分杆件横截面上一点处的总应力，可分解为 应力和 应力。

14、A01 B03 杆件的横向变形和应变 拉压杆的应力变形 2分4B轴向拉伸或压缩杆件中，ε为纵向线应变，ε'为横向线应变，μ为杆件材料的泊松比。

工程力学课程标准一、课程性质、任务和基本任务1.课程的性质工程力学是一门应用非常广泛的技术基础课。

它一方面可以直接解决工程中的受力分析、运动计算、强度计算和刚度计算问题，另一方面也为一系列后继课程如机械原理、机械设计、汽车构造等提供必备的基础知识。

随着科学技术的发展，很多科学领域的研究都需要工程力学的知识。

所以，工程力学是工程技术人员必备的理论基础。

2.任务和基本要求1）会进行物体的受力分析和求解工程中的平衡为题；2）理解速度、加速度、角加速度、绝对速度、相对速度、牵连速度的概念；会求定轴转动刚体上的速度和加速度；3）了解材料的力学性能；掌握四种基本变形、应力集中和交变应力、压杆稳定的概念；会进行四种基本边线构件的强度计算。

二、课程教学目标按照五年制高职汽车运用技术及相关专业的教学计划的要求，本课程主要讲授静力学、平面汇交力系、力矩与平面力偶系、平面任意力系、摩擦、空间力系、点的运动、刚体的基本运动、点的合成运动、轴向拉伸与压缩、剪切和挤压、圆轴的扭转、直梁弯曲、组合变形的强度计算、动载荷与交变应力等内容。

三、学习内容及要求1）绪论了解工程力学课程的性质、任务和主要内容；了解工程力学的研究对象：机械部件一主要是杆件；了解工程力学中轴向拉伸和压缩、剪切和挤压、扭转、弯曲四种基本变形的强度、刚度问题熟悉课程的性质、任务和基本要求。

（二）静力学基础主要内容：1 .力学的基本概念和公理；2 .约束的概念、特点、约束反力、工程结构及其简化；3 .物体的受力分析和绘制物体的受力图。

教学目标：1 .了解静力学的一些基本概念和公理；2 .掌握约束及其基本类型的结构和简图并确定约束反力；3 .能应用所学知识进行物体的受力分析并会绘制物体的受力图。

（三）平面汇交力系主要内容：1 .几何法一一力的多变形法；2 .解析法；3 .平面汇交力系平衡的几何条件和解析条件。

教学目标：1 .会用力多边形法求合力；2 .会用解析法求合力；3 .能用平衡方程求解工程问题，（四）力矩与平面力偶系主要内容：1 .力矩的概念及计算；2 .力偶、力偶矩；3 .力的平移。

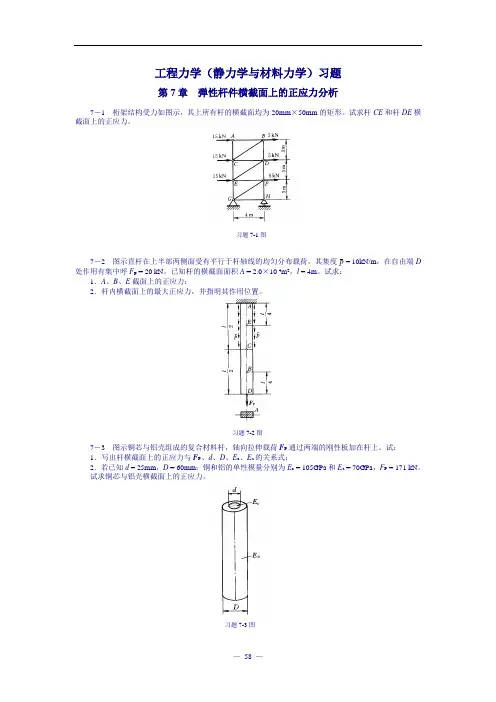
习题7-1图习题7-2图 习题7-3图工程力学（静力学与材料力学）习题第7章 弹性杆件横截面上的正应力分析7－1 桁架结构受力如图示，其上所有杆的横截面均为20mm ×50mm 的矩形。

试求杆CE 和杆DE 横截面上的正应力。

7－2 图示直杆在上半部两侧面受有平行于杆轴线的均匀分布载荷，其集度p = 10kN/m ，在自由端D 处作用有集中呼F P = 20 kN 。

已知杆的横截面面积A = 2.0×10-4m 2，l = 4m 。

试求：1．A 、B 、E 截面上的正应力；2．杆内横截面上的最大正应力，并指明其作用位置。

7－3 图示铜芯与铝壳组成的复合材料杆，轴向拉伸载荷F P 通过两端的刚性板加在杆上。

试：1．写出杆横截面上的正应力与F P 、d 、D 、E c 、E a 的关系式；2．若已知d = 25mm ，D = 60mm ；铜和铝的单性模量分别为E c = 105GPa 和E a = 70GPa ，F P = 171 kN 。

试求铜芯与铝壳横截面上的正应力。

习题7-4图 习题7-5图 习题7-6图习题7-7图 7－4 图示由铝板钢板组成的复合材料柱，纵向截荷F P 通过刚性平板沿着柱的中心线施加在其上。

试：1．导出复合材料柱横截面上正应力与F P 、b 0、b 1、h 和E a 、E s 之间的关系式；2．已知F P = 385kN ；E a = 70GPa ，E s = 200GPa ；b 0 = 30mm ，b 1 = 20mm ，h = 50mm 。

求铝板与钢板横截面上的最大正应力。

7－5 从圆木中锯成的矩形截面梁，受力及尺寸如图所示。

试求下列两种情形下h 与b 的比值：1．横截面上的最大正应力尽可能小；2．曲率半径尽可能大。

7－6 梁的截面形状为正方形去掉上、下角，如图所示。

梁在两端力偶M z 作用下发生弯曲。

设正方形截面时，梁内最大正应力为0σ；去掉上、下角后，最大正应力变为0max σσk =，试求：1．k 值与h 值之间的关系；2．max σ为尽可能小的h 值，以及这种情形下的k 值。

《材料力学》课程中杆件内力与变形计算的Matlab实现李春锋;蒲兴龙;于彬;杨旭辉;王丽【摘要】杆件的内力与变形计算是材料力学课程教学的主要任务之一，其确定往往涉及较大的计算量，学生在学习中易形成重计算而轻力学原理与力学思想的学习观念。

将Matlab科学计算软件引入材料力学课程，将杆件内力与变形中比较繁杂的数学运算由计算机完成，一方面能使学生将大量时间用于掌握力学原理和力学思想，提高教学质量和教学效果，另一方面对培养学生用计算机解决问题与创新能力的提高有着积极的推动作用，为相关力学类课程的教学与学习提供一些参考。

%Internal forces and deformation calculation of the prismatic bar is one of the main tasks of mechanics of materials,and its calculation often takes much time. Hence, many students spend much time learning the calculation but neglect the learning of the mechanical calculation principle and mechanics. However, there’re solutions of putting the Matlab scientific computing software into the material mechanics course and making more complex mathematical operations done by the computer on internal forces and deformation calculation, which enable students to focus on the principles of mechanics and mechanical thinking,which also improve teaching quality and teaching effectiveness. In addition, students are promoted to use computers actively to solve problems and to improve their innovation capability. And the solutions also provide some reference for the teaching and learning of other mechanics courses.【期刊名称】《河西学院学报》【年(卷),期】2015(000)002【总页数】12页(P55-65,9)【关键词】材料力学;内力;变形;Matlab;计算【作者】李春锋;蒲兴龙;于彬;杨旭辉;王丽【作者单位】河西学院土木工程学院，甘肃张掖734000;河西学院土木工程学院，甘肃张掖 734000;河西学院土木工程学院，甘肃张掖 734000;河西学院土木工程学院，甘肃张掖 734000;河西学院土木工程学院，甘肃张掖 734000【正文语种】中文【中图分类】O3材料力学课程是土木、机械等专业的核心基础课程，传统力学类课程教学及学习过程中经常要面对大量而繁杂的数学计算，使得教学、学习过程中容易产生重计算而轻视或忽略力学模型的建立及力学原理的学习，其已经暴露出许多不尽如人意的方面，国内很多理工科院校在材料力学课程的教学中进行了较多的探讨与研究.将计算机技术与现代数值计算方法引入材料力学课程的教学，给力学类课程的教学提供了新的教学视野，对提高教学质量，加强学生力学建模与力学原理思想及培养学生创新思维提供了积极的因素.Matlab软件以其强大的计算与图形仿真能力正逐渐成为理工科大学本科生、硕士生、博士生必需掌握的基本技能之一，国内很多学者已将其引入到力学类课程教学中并取得了丰富的成果.罗义银、邓旭辉等［1-4］通过运用Matlab来分析运动学、动力学问题来讲述Matlab在理论力学教学中的运用，李银山［5-6］将 Maple软件作为学习理论力学、材料力学的工具，并将之编写为教材，王玉山等［7］介绍了Matlab在材料力学超静定问题求解及梁变形可视化中的应用，张宁等［8］利用Simmechanics对曲柄连杆机构进行了运动学和动力学仿真，敖文刚［9］利用Matlab设计了虚拟实验可视化用户界面，可将分析结果以曲线动画和表格表达出来.内力与变形计算是《材料力学》课程教学的重要内容，采用Matlab软件进行较为系统的构件、简单结构内力与变形计算的研究还不是很多，较系统的对材料力学课程中的拉压、扭转、弯曲及梁的剪力与弯矩问题进行计算机分析仿真，并利用Matlab自身强大的数据图形处理能力对分析结果以图形输出，使学生能在课堂上直观了解工程实际问题的处理过程，既可提高学生的学习兴趣，又可增强学生对工程实际的感性认识和解决工程问题的能力，对《材料力学》课程的教学方法改革将有着重要的补充意义.1.1 静定问题1.1.1 拉（压）杆件计算的Matlab仿真（1）计算方法拉压杆的内力与应力计算是《材料力学》课程四种基本计算内容之一.对于常见的杆系结构，其求解往往涉及线性方程组的求解，耗时耗力.运用Matlab软件只需针对所建立力学模型列出方程（组），运用Matlab软件下的solve命令即可得到结果.其计算的基本思路可概括如下：①确定荷载；②画受力分析图；③静力平衡方程，求解.（2）举例与Matlab仿真计算例题1：如图1所示，实心圆钢杆AB和AC在点A铰接连接，在A点作用有铅垂向下的力F= 35KN.已知杆AB和AC的直径分别为d1=12mm和d2=15mm，钢的弹性模量E=210Gpa.试求各杆轴力及A点的铅垂位移.Matlab程序：%考虑节点位移问题；以水平向右为X正方向1.1.2 等直圆杆的扭转计算与Matlab仿真（1）计算方法等直圆杆扭转时的应力计算，需要先从变形几何方面和物理方面两方面确定切应力在横截面上的分布规律，然后再考虑静力平衡进行求解.几何方面通过一点处切应变随该点在横截面上的位置变化而变化的规律，通过下面公式计算.在物理方面，由剪切胡克定律可知，在线弹性范围内，切应力与切应变成正比计算，即在静力学方面，由合力矩原理可得扭矩T.结合三方面便可算出等直圆杆在扭转时的切应力.其计算的基本思路可概括为：①确定作用在圆杆上的外力偶；②列静力平衡方程；③求解并画扭矩图.（2）举例与Matlab仿真计算例题2：一传动轴如图2所示，其转速n=300r/min，主动轮输入的功率P1=500kW.若不计轴承摩擦所耗的功率，三个从动轮输出的功率分别为P2=150kW，P3=150kW及P4=200kW，试做轴的扭矩图.运行结果：如图2所示.1.1.3 静定梁的计算与仿真（1）计算方法梁截面内力求解的基本方法是截面法，工程常根据梁截面内力图以确定梁构件的配筋计算图，依据所绘制梁的内力图，一方面可直观地确定出梁的“危险点”、“危险截面”.另一方面是完成梁的截面尺寸设计和强度、刚度校核的关键环节.其计算的基本思路可概括如下：①计算支座约束力；②建立剪力函数（剪力的单位kN）；③建立弯矩函数（弯矩的单位kN·m）；④绘制剪力图；⑤绘制弯矩图；（2）举例与Matlab仿真计算例题3：已知简支梁上均布荷载与力偶共同作用时，Me=4KN.m，q=0.2KN/m，l=10m，b=2m，绘制其剪力及弯矩图，计算简图如图3所示.运行结果：如图3所示.1.2 超静定问题1.2.1 拉（压）杆件超静定问题计算与Matlab仿真（1）计算方法实际工程中，大多数杆件结构为超静定结构，其特点是未知力的数目多于独立静力平衡方程的数目，在计算时首先要确定体系的超静定次数，根据变形协调条件，得出补充方程，再依据平衡条件求出未知力，最后得到结构体系的内力图，计算思路简单，但计算量非常之大.其常用基本计算思路可概括如下：①确定荷载；②画受力分析图，确定超静定次数并列静力平衡方程；③建立杆件的变形方程（几何关系）；④建立物理方程（力与变形之间的关系）；⑤求解.（2）举例与Matlab仿真计算例题4：如图4所示，支架承受荷载F=10KN，1、2、3各干由同一材料制成，其横截面积分别为A1=100mm2，A2=150mm2和A3=200mm2.试求各杆轴力.1.2.2 扭转超静定计算与Matlab仿真（1）计算方法扭转变形是结构体系中杆件的基本变形之一，工程中的大部分构件在正常工作阶段需考虑其扭转效应，扭转超静定问题比简单的扭转问题更为复杂，需要考虑杆件在扭转时的几何条件、物理条件，然后联合求解.其计算的基本思路可概括如下：①确定荷载；②画受力分析图，确定超静定次数并列静力平衡方程；③建立杆件的变形方程（几何关系）；④建立物理方程（力与变形之间的关系）；⑤联合求解.（2）举例与Matlab仿真计算例题5：如图5所示，圆截面杆AC的直径d1=100mm，A端固定，在截面B承受外力偶矩Me= 7kN.m，截面C的上、下两点处的直径均为d2=20mm的圆杆EF、GH铰接.已知各杆件材料相同，弹性常数间的关系为G=0.4E.试求杆AC的最大切应力.Matlab程序：%考虑杆件的扭转问题1.2.3 简单超静定梁的计算与Matlab仿真（1）计算方法在超静定梁的计算中，需要运用变形计算法来对其求解，确定超静定次数是解决此问题的首要条件，超静定次数决定了补充方程的个数，将梁所受的约束去掉加为未知力，根据叠加原理求解此问题.其解决思路可概括如下：①确定超静定次数；②确定静定基（去约束，加未知力）；③建立补充方程（变形条件）；④联合静力方程求解；⑤绘制内力图.（2）举例与Matlab仿真计算例题6：如图6所示，矩形梁AB受到均布荷载q=5kN/m的作用，其梁的截面尺寸为b=250mm，h=500mm，梁的跨度为l=6m，弹性模量E=210Gpa.绘制梁的内力图.2.1 拉（压）杆件的变形计算与Matlab仿真（1）计算方法拉压杆件的变形计算主要以轴向变形与横向变形为主，其主要计算思路可概括如下：①确定荷载，用截面法确定杆件的轴力.②由于材料力学范围内主要讨论线弹性范围内变形，故广义胡克定律成立，可用下述公式来计算出轴线方向的变形.③由所求的轴向变形根据泊松比即可计算出杆件在拉压时的横向变形.（2）举例与Matlab仿真计算例题7：图7所示结构中AB为水平放置的刚性杆，杆1、2、3材料相同，其弹性模量为E= 210Gpa，已知l=1m，A1=A2=A3=100mm2，F=20kN.求C点的水平位移与铅垂位移.解题思路：设图示中各杆件受拉为正，C点因各杆变形而引起X方向位移，Y方向位移.①由胡克定律，得杆件变形表达式为：②节点的变形几何关系为：式中，ls表示水平位移，lv表示竖直位移，由于3杆为刚性杆，故不发生形变.③由于以上计算均为线性方程，可利用Matlab矩阵左除命令求解.2.2 等直圆杆的扭转变形计算与Matlab仿真（1）计算方法等直圆杆扭转时的变形为一端固定不动，另一端相对固定端扭转角来表现.主要计算思路如下：①确定扭矩，运用截面法通过已知的外力偶确定杆件内部的扭矩.②根据已知杆件尺寸确定杆件极惯性矩IP.③圆轴扭转的变形（扭转角）可根据下列公式确定.对于扭转问题来说，通常极惯性矩的计算是在扭转变形计算中是非常繁琐且耗费大量时间，而在Matlab中只需根据不同类型的杆件来选择相应的计算方法，之后便是矩阵形式的线性方程组的运用，大大的简化了复杂的计算过程.（2）举例与Matlab仿真计算例题8：已知Ma=5.4kN.m，Mb=1.8kN.m，Mc=3.6kN.m，G=80×103pa，D=125mm，d=100mm，计算扭转角Φ.解题思路：首先，通过外力偶计算杆件扭矩T.其次，由于是空心圆杆，故采用下列公式来计算其极惯性矩.最后，将求得的极惯性矩以及扭矩代入扭矩下述公式，即可计算出杆件的转角. 2.3 静定梁的变形计算与Matlab仿真（1）计算方法静定梁变形的主要指标是：挠度和转角.其主要的计算思路如下：①确定荷载，确定杆件上作用的剪力及弯矩.②写出杆件的弯矩方程.③对弯矩方程一次积分得到转角方程且含有未知常数C，再次积分得到杆件的挠度方程且含有未知常数C和D.④利用杆件特殊位置的挠度与转角的边界条件，求出未知数C，D.⑤将所求位置点代入挠度转角方程，即可得到所求的挠度与转角方程.在静定梁的变形计算中最为繁琐之处在于采用积分方法确定挠度与转角的方程，积分会耗费大量的时间且容易出错，运用Matlab强大的计算能力，可以用计算机来计算积分，从而得到变形方程，节省大量时间.（2）举例与Matlab仿真计算例题9：如图8所示，一悬臂梁在端部受集中力F=10kN作用，其梁的截面尺寸为b=250mm，h= 500mm，梁的跨度为l=3m，弹性模量E=210Gpa.求梁的转角和挠度并绘制变形曲线.通过上面分析可以看出，《材料力学》课程中引入Matlab编程功能，进行杆件或杆系结构内力与变形计算将对课程的教学与学生学习、创新能力的培养有着积极的作用，具体为：（1）使学生从力学类课程繁杂的数学手算中解脱出来，将课程学习的主要精力集中到力学建模与力学分析思路的养成上，把繁杂的计算任务交给计算机去完成. （2）通过Matlab科学计算平台，引导学生建立数值求解的思想和方法，提高学生的工程素养与工程意识.（3）Matlab软件在课程教学中的引进，有利于提高教学效率，加强学生对基本概念和原理的理解，为学生创新思维的发挥拓展了广阔的空间，给学生自主学习和研究性学习提供了一个良好的平台，为相关力学类课程教学与学习提供一些参考.【相关文献】［1］罗义银.机械类专业理论力学教学改革的发展与思考［J］.力学与实践，2000，22（3）：56-57.［2］邓旭辉，张平，肖攀.Matlab在理论力学教学中应用［J］.力学与践，2006，28（5）：82-83.［3］胡超，程建钢.《理论力学》多媒体仿真教学实验［J］.力学与实践，2003，25（1）：67-70.［4］李校兵，扬芳，王军.Matlab在理论力学教学中的应用［C］.2009力学课程报告论坛论文集，2009：63-65.［5］李银山.Maplel理论力学［M］.北京：机械工业出版社，2006.［6］李银山.Maplel材料力学［M］.北京：机械工业出版社，2009.［7］王玉山，王锐.Matlab在材料力学超静定问题求解及梁变形可视化中的应用［J］.石河子大学学报，2007，25（1）：109-111.［8］张宁，田杰，陈奇.基于simmechanics的曲柄压力机机构仿真分析［J］.宜春学院学报，2013，35（3）：35-36.［9］敖文刚.基于Matlab的可视化理论力学虚拟实验［J］.重庆工商大学学报：自然科学版，2012，29（9）：101-105.［10］孙训方，方孝淑，关来泰.材料力学（Ⅰ）［M］.北京：高等教育出版社，2013.。

习题10-1图(a) 习题10-2图(a)工程力学（工程静力学与材料力学）习题与解答第10章 杆件横截面的位移分析10－1 直径d = 36mm 的钢杆ABC 与铜杆CD 在C 处连接，杆受力如图所示。

若不考虑杆的自重，试： 1．求C 、D 二截面的铅垂位移；2．令F P1 = 0，设AC 段长度为l 1，杆全长为l ，杆的总伸长EA lF l 2P =∆，写出E 的表达式。

知识点：拉压杆件的变形与位移 难度：一般 解答：（1）4π)(4π)(2sN 2sN d E l F d E l F u u BC BC AB AB A C ++=947.236π41020030001010020001015002333=⨯⨯⨯⨯⨯+⨯⨯+=mm286.536π101054250010100947.24π)(2332cN =⨯⨯⨯⨯⨯⨯+=+=d E l F u u CD CD C D mm（2）AE l lF A E l F l l l EA l F CD AC c 12P s 12P 2P )(-+=∆+∆=∆=cs 11E E E ηη-+= sc sc )1(E E E E E ηη-+= 令l l 1=η10－2 承受自重和集中载荷作用的柱如图所示，其横截面积沿高度方向按P0e)(0F xA A x A ρ=变化，其中ρ为材料的比重。

试作下列量的变化曲线： 1．轴力)(N x F x ； 2．应力)(x x σ； 3．位移)(x u 。

知识点：拉压杆件的变形与位移 难度：一般 解答：（1）0=∑ξ，0d )()d (N N N =-++F A F F ξξρ习题10-3图 N F(a) x x (b) ξρξξρξρd ed )(d P00N F A A A F -=-=ξρξρd ed P0N P0)(-N F A xx F F A F ⎰⎰-=P0P0e)e()(P P P P N F xA F xA F F F F x F ρρ-=---=（2）0P 0P N P0P 0e e )()()(A FA F x A x F x F xA F xA -=-==ρρσ （3）⎰⎰⎰⎰-=-==P 0P N P0P0ee )(d )(d EAdxF dx EA F x EA xx F u F xA F xA ρρC EA x F u +-=0P ，当0|==l x u 。

工程力学 静力学与材料力学 (单辉祖 谢传锋 著） 高等教育出版社 课后答案1-1试画出以下各题中圆柱或圆盘的受力图。

与其它物体接触处的摩擦力均略去。

解:1—2 试画出以下各题中AB 杆的受力图。

(a)(b)(c)(d)(e)A(a)(b) A(c)A(d)(e)(c)(a)(b)解：1-3 试画出以下各题中AB 梁的受力图。

解：(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)(a)F(b)WA(c)（a ） 拱ABCD ；(b) 半拱AB AB ；(e) 方板ABCD ；（f ） 节点B.解:1—5 试画出以下各题中指定物体的受力图。

(a ） 结点A ,结点B ；(b ） 圆柱A 和B 及整体；（c ） 半拱AB ，半拱BC 及整体;(d) 杠杆AB ，切刀CEF 及整体；(e) 秤杆AB ，秤盘架BCD 及整体。

(d)D(e)F Bx(a)(b)(c)(d)(e)W(f)(a)D(b) CB(c)BF D (d) F C(e)B (f)F F BC解：(a ）(b)(c ）(d)(c)(d)ATFBAFCAACD(e)(e ）2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示,F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重,试求两杆所受的力。

解：（1） 取节点C 为研究对象，画受力图，注意AC 、BC 都为二力杆，(2) 列平衡方程:12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。

2-6 如图所示结构由两弯杆ABC 和DE 构成。

构件重量不计，图中的长度单位为cm 。

已知F =200 N ，试求支座A 和E 的约束力。

BF 1F解：（1) 取DE 为研究对象,DE 为二力杆；F D = F E(2) 取ABC 为研究对象，受力分析并画受力图；画封闭的力三角形:'15166.7 23A D E F F F F N ===⨯= 3—1 已知梁AB 上作用一力偶，力偶矩为M ，梁长为l ，梁重不计。