线 性 规 划 算 法 详 解
- 格式:pdf
- 大小:310.79 KB
- 文档页数:25



优化物流路线规划与管理第1章物流路线规划基础 (4)1.1 物流与供应链管理概述 (4)1.1.1 物流的概念与功能 (4)1.1.2 供应链管理的发展 (4)1.2 路线规划的重要性 (4)1.2.1 降低物流成本 (4)1.2.2 提高物流效率 (4)1.2.3 提升服务水平 (4)1.3 路线规划的基本原理 (4)1.3.1 运输距离最短原则 (4)1.3.2 货物集中配送原则 (5)1.3.3 时间窗约束原则 (5)1.3.4 网络优化原则 (5)1.3.5 面向客户原则 (5)第2章物流运输网络构建 (5)2.1 运输网络结构设计 (5)2.1.1 运输网络基本构成要素 (5)2.1.2 运输网络结构设计原则 (5)2.1.3 运输网络结构设计方法 (6)2.2 运输网络优化方法 (6)2.2.1 运输问题求解方法 (6)2.2.2 运输网络优化策略 (6)2.3 运输网络案例分析 (6)2.3.1 案例一:某电商企业物流运输网络优化 (6)2.3.2 案例二:某跨国公司全球物流运输网络构建 (6)2.3.3 案例三:某城市公共交通网络优化 (7)第3章货运车辆路径问题 (7)3.1 货运车辆路径问题概述 (7)3.1.1 定义与背景 (7)3.1.2 分类 (7)3.1.3 研究意义 (7)3.2 车辆路径问题的求解方法 (7)3.2.1 启发式算法 (7)3.2.2 精确算法 (8)3.2.3 元启发式算法 (8)3.3 车辆路径问题的优化策略 (8)3.3.1 集中配送策略 (8)3.3.2 分区配送策略 (8)3.3.3 多车型协同配送策略 (8)3.3.4 考虑时间窗的配送策略 (8)3.3.5 绿色配送策略 (8)第4章时间窗约束下的物流路线规划 (8)4.1 时间窗约束概述 (8)4.2 带时间窗的车辆路径问题 (9)4.3 时间窗约束下的路径优化算法 (9)第5章多目标物流路线规划 (9)5.1 多目标优化概述 (9)5.1.1 多目标优化的定义与意义 (9)5.1.2 多目标优化方法与策略 (9)5.2 多目标物流路线规划方法 (9)5.2.1 基于遗传算法的多目标物流路线规划 (9)5.2.2 基于粒子群算法的多目标物流路线规划 (9)5.2.3 基于蚁群算法的多目标物流路线规划 (10)5.3 多目标优化算法应用 (10)5.3.1 多目标优化算法在物流配送中的应用 (10)5.3.2 基于多目标优化算法的物流网络设计 (10)5.3.3 多目标优化算法在跨境电商物流中的应用 (10)第6章集成物流路线规划与调度 (10)6.1 集成物流管理概述 (10)6.1.1 集成物流管理的概念 (10)6.1.2 集成物流管理的重要性 (10)6.2 路线规划与调度集成方法 (10)6.2.1 车辆路径问题(VRP)概述 (10)6.2.2 集成遗传算法与禁忌搜索的路线规划方法 (11)6.2.3 集成粒子群优化与模拟退火算法的车辆调度方法 (11)6.3 集成优化策略与应用 (11)6.3.1 集成优化策略概述 (11)6.3.2 集成优化策略在物流领域的应用 (11)6.3.3 集成优化策略的发展趋势 (11)第7章绿色物流与路径规划 (11)7.1 绿色物流概述 (11)7.1.1 绿色物流的定义与内涵 (11)7.1.2 绿色物流的发展背景与意义 (11)7.1.3 绿色物流的核心要素与挑战 (11)7.2 考虑碳排放的物流路线规划 (11)7.2.1 碳排放与物流活动的关系 (11)7.2.2 碳排放核算方法在物流领域的应用 (11)7.2.3 考虑碳排放的物流路线规划模型 (12)7.2.4 碳排放约束下的物流路线优化策略 (12)7.3 绿色物流路径优化方法 (12)7.3.1 节能减排的物流路径规划方法 (12)7.3.1.1 节能型车辆选用与调度 (12)7.3.1.2 低碳运输方式选择与协同 (12)7.3.1.3 路径规划中的能耗评估与优化 (12)7.3.2 基于可持续发展理念的物流路径规划方法 (12)7.3.2.1 可持续发展目标下的物流路径规划原则 (12)7.3.2.2 多目标优化方法在物流路径规划中的应用 (12)7.3.2.3 生态补偿机制在物流路径优化中的作用 (12)7.3.3 基于大数据分析的绿色物流路径优化方法 (12)7.3.3.1 大数据在物流路径规划中的应用 (12)7.3.3.2 数据驱动的绿色物流路径优化策略 (12)7.3.3.3 基于实时交通信息的物流路径动态调整 (12)7.3.4 基于物联网技术的绿色物流路径优化方法 (12)7.3.4.1 物联网技术在物流路径规划中的应用 (12)7.3.4.2 智能配送系统与路径优化 (12)7.3.4.3 物联网环境下物流路径规划的挑战与对策 (12)第8章基于大数据的物流路线优化 (12)8.1 大数据在物流领域的应用 (12)8.1.1 大数据的定义与特征 (12)8.1.2 物流行业大数据的来源与类型 (12)8.1.3 大数据在物流行业的价值体现 (12)8.1.4 大数据技术在物流领域的应用现状 (12)8.2 基于大数据的路径规划方法 (12)8.2.1 数据预处理技术 (12)8.2.2 路径规划算法 (13)8.2.3 基于大数据的路径规划模型 (13)8.3 数据驱动的物流路线优化策略 (13)8.3.1 实时动态路径规划 (13)8.3.2 货运车辆调度优化 (13)8.3.3 集成物流信息平台 (13)8.3.4 大数据技术在物流配送中的应用案例分析 (13)第9章智能物流与路径规划 (14)9.1 人工智能技术概述 (14)9.2 智能物流路径规划方法 (14)9.3 机器学习在物流路径优化中的应用 (14)第10章物流路线规划与管理的实践与展望 (14)10.1 物流路线规划与管理案例分析 (14)10.1.1 案例选取与背景介绍 (14)10.1.2 物流路线规划实践过程 (14)10.1.3 物流路线管理策略分析 (14)10.1.4 案例成果与经验总结 (14)10.2 物流路线规划与管理的挑战与机遇 (14)10.2.1 国内外物流市场环境分析 (14)10.2.2 物流路线规划与管理的核心问题 (14)10.2.3 面临的主要挑战及其成因 (15)10.2.4 把握物流产业发展机遇 (15)10.3 未来发展趋势与展望 (15)10.3.1 物流路线规划技术的创新 (15)10.3.2 物流管理模式的变革 (15)10.3.3 绿色物流与可持续发展 (15)10.3.4 智能化、信息化在物流路线管理中的应用 (15)10.3.5 跨境电商与物流路线规划的新需求 (15)10.3.6 物流路线规划与国家战略的融合 (15)第1章物流路线规划基础1.1 物流与供应链管理概述1.1.1 物流的概念与功能物流作为现代企业运营的重要组成部分,涉及原材料的采购、产品的生产、仓储、配送以及售后服务等多个环节。

如何进行线形工程量测算与统计分析线形工程量的测算与统计分析是在工程领域非常重要的一项工作。
准确的测算和分析能够为工程项目的规划、设计和施工提供重要的参考依据。
本文将探讨如何进行线形工程量的测算与统计分析,包括测算方法、统计分析的指标和方法等。
一、线形工程量的测算方法线形工程量的测算是指根据工程项目的设计图纸或现场实际情况,通过对工程线形进行测量,计算出相应的工程量。
线形工程量通常包括路基、路面、排水、交通设施等方面的工程量。
1.1 路基工程量的测算方法路基工程量的测算主要是指道路的开挖和填方量。
测算方法一般有平面测量法和剖面测量法两种。
平面测量法是通过在道路布置测量控制点,利用全站仪进行距离和高差测量,然后计算各个测量截面的面积,最终得到开挖和填方量。
剖面测量法是通过在道路横断面上布置一定数量的测量点,在每个测量点上进行高程测量,然后计算每个测量点的填挖方量,最后累加得到总的开挖和填方量。
1.2 路面工程量的测算方法路面工程量的测算主要是指路面材料的用量和面积。
测算方法一般有直接测算法和母线法两种。
直接测算法是通过在路面布置测量控制点,利用全站仪进行面积测量和高程测量,然后根据标准设计厚度计算路面材料的用量。
母线法是在道路纵断面上布置一定数量的测量点,然后通过对这些测量点的高程测量,计算出道路纵断面的曲线形状,最后根据标准设计厚度计算路面材料的用量。
二、线形工程量的统计分析指标线形工程量的统计分析是指对测算得到的工程量进行合理的分析和统计,以便为工程项目的施工和管理提供参考依据。
常用的统计分析指标包括工程量累计曲线、施工进度分析和工程量变化趋势等。
2.1 工程量累计曲线工程量累计曲线反映了工程项目的施工进度和完成情况。
通过绘制工程量累计曲线,施工管理者可以清晰地了解到工程量的完成情况和施工进度的变化趋势,以便及时采取相应的措施调整施工进度。
2.2 施工进度分析施工进度分析是对工程项目的施工进度进行定量分析和评估。


划线工具及其使用方法常用的划线工具:有钢直尺、划线平台、划针、划线盘、高度游标卡尺、划规、样冲、V型架、角尺和角度规及千斤顶或支持工具等。
1. 钢直尺:主要用来量取尺寸、测量工件以及作划直线时的导向工具。
钢直尺是一种简单的尺寸量具。
在尺面上刻有尺寸刻线,最小刻线距为0.5mm,其长度规格有150mm,300mm,1000mm等多种。
2. 划线平台(划线平板)用来安放工件和划线工具:(1) 划线平台的制造材料:划线平台一般由铸铁制成,工作表面经过精刨或刮研等精加工,作为划线时的基准平面。
划线平台—般在平板支架上搁置,放置时应使平台工作表面处于水平状。
(2) 划线平台的使用要求:①工作表面应保持水平安装,划线平台要使表面保持水平状态,以免倾斜后在长期的使用状态下发生变形。
使用时要随时保持平台工作表面清洁,避免铁屑、灰砂等污物在划线工具或工件的拖动下划伤平台表面,影响划线精度。
用后要擦拭干净,并涂上机油防锈。
②要轻拿轻放物品,防止撞击平台工作表面,工件和工具在平台上都要轻拿轻放,尤其要防止重物撞击平台和在平台上进行敲击而损伤平台工作面。
3.划针用来在工件上划线条:(1)划针的制造材料:划针通常是用弹簧钢丝或高速钢制成,一般直径为3~5mm,长度约为200~300mm,尖端磨成15°~20°的尖角,并经热处理淬火使之硬化,这样就不容易磨损变钝。
有的划针在尖端部位焊有硬质合金,耐磨性更好。
(2)划针的使用要求:①针尖要紧靠导向工具的边缘,上部向外侧和划线方向倾斜划线用划针划线时,针尖要紧靠导向工具的边缘,压紧导向工具,避免滑动面影响划线的准确性。
划针的握法与用铅笔划线相似,上部向外侧倾斜15°~20°,向划线移动方向倾斜约45°~75°。
在用钢尺和划针划连接两点的直线时,应先用划针和钢尺定好后一点的划线位置,然后凋整钢尺使与前一点的划线位置对准,再开始划出两点的连接直线。



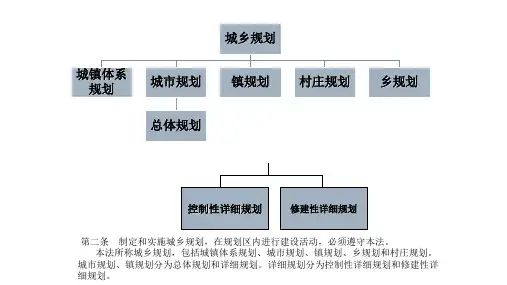

详细规划(一)城市详细规划的编制分为控制性详细规划和修建性详细规划两个层次。
第一层次的控制性详细规划重点是确定用地功能的组织,制定各项规划控制条件,第二层次的修建性详细规划重点是进行建筑与设施的具体布局。
修建性详细规划一般应该在控制性详细规划确定的规划指导下编制,修建性详细规划直接对建设项目和周围环境进行具体安排和规划设计,主要确定各类建筑、各项基础工程设施、公共服务设施的具体配置,并根据建筑和绿化的空间布局进行环境景观设计,为各项建筑工程的初步设计和施工图设计提供依据。
一控制性详细规划概述控制性详细规划是衔接总体规划,分区规划的宏观要求与指导修建性详细规划编制的承上启下的编制层次,它既是编制修建性详细规划的主要指导性文件,又是城乡规划管理、土地开发的重要技术依据。
它以城市总体规划或分区规划为依据,确定建设用地的土地使用性质,和使用强度的控制性指标,道路和管线控制性位置和空间环境控制的规划;以土地利用控制为重点,其规划设计考虑了规划管理的要求,房地产开发的衔接,有利于规划管理实现规范化和法制化。
1. 控制性详细规划的作用1)承上启下控制性详细规划是连接总体规划与修建性详细规划的的承上启下的关键性编制层次,是规划管理、规划与实施衔接的重要环境,是规划管理的依据,是体现城市设计构想的关键。
城市总体规划是一定时期内城市发展的总体战略框架,必须具有很大程度上的原则性与灵活性,是一种粗线条的框架规划,需要下一层次的规划将其深化才能真正发挥作用。
修建性详细规划是对小范围内城市开发建设活动进行总平面布局和空间立体组织,需要上一层次的规划对用地性质和开发强度进行控制,对开发模式和城市景观进行引导,因此,控制性详细规划是两者之间有效的过度与衔接,起到深化前者和控制后者的作用,确保规划体系的完善和链接。
2)规划管理的依据和城市开发的引导2006年4月1日建设部正式施行的《城市规划编制办法》明确了控制性详细规划的编制要求和内容。
20XX 年高考数学答题规范与技巧高考答题的规范化要求有好多方面:答题工具、答题规则与程序、答题地点、答题过程及书写格式要求等。
养成优秀的答题习惯,能够帮助考生多得分,最少不会失掉一些应得分。
1.答题工具①答选择题时,一定用合格的 2B 铅笔填涂,如需要对答案进行改正,应使用画图橡皮轻擦洁净,注意不要擦破答题卡。
②严禁使用涂改液、修正带或透明胶带改错。
③非选择题一定用 0.5 毫米黑色墨水署名笔作答,作图题可先用铅笔绘出,确认后,再用 0.5 毫米黑色墨水署名笔描清楚。
2.答题规则与程序⑴先选择题、填空题,再做解答题;⑵先填涂再解答;⑶先易后难。
3.答题地点按题号在指定的答题地区内作答,切不行高出黑色边框,高出黑色边框的答案无效。
如需对答案进行改正,可将需改正的内容划去,而后紧挨在其上方或其下方写出新的答案,改正部分在书写时与正文同样,不可以超出该题答题地区的黑色矩形边框,不然改正的答案无效。
一般先紧后松。
4.解题过程及书写格式要求⑴选择题的填涂⑵填空题的规范对于填空题,只需填写结果,省掠过程,并且所填结果应力求精练、归纳的正确。
常有错误或不规范的答卷方式有:笔迹不工整、不清楚、字符书写不规范或不正确、分式写法不规范、通项和函数表达式书写不规范、函数分析式书写正确但不注明定义域、要求结果写成会合的不用会合表示、会合的对象属性描绘不正确。
⑶解答题的规范第一,解答题应答时,考生不单要供给出最后的结论,还得写出或说出解答过程的主要步骤,供给合理、合法的说明。
答题过程要整齐雅观、逻辑思路清楚、观点表达正确、答出重点语句和重点词。
比方要将你的解题过程转变为得分点,主要靠正确完好的数学语言表述,这一点常常被一些考生忽略,所以,卷面上大批出现“会而不对”“对而不全”的状况。
如立体几何论证中的“跳步”,使好多人丢掉得分,代数论证中的“以图代证”,只管解题思路正确甚至很奇妙,可是因为不擅长把“图形语言”正确地转移为“文字语言”,只管考生“成竹在胸”却说不清楚,所以得分少。
城市的规划“五线”--红线、绿线、蓝线、紫线、黄线城市规划“五线”“五线”管制属城市规划得强制性内容,适⽤于从城市总规到控制性详规等不同层⾯得城市规划。
“五线”管制制度,分别⽤“红线”、“绿线”、“蓝线”、“紫线”与“黄线”划定城市建设中得“雷区”,凡就是被划定得区域,城市建设不得随意侵占,区域内各项建设将受到严格控制,能有效避免重复建设,提⾼城市建设质量。
“红线”划定规划管理部门批准得建设⽤地,主要针对道路控制⽽设⽴。
“绿线”就是指城市各类绿地范围得控制线。
“蓝线”就是指城市江河湖泊⽔域控制线。
“紫线”就是指各类历史⽂化遗产与风景名胜资源保护控制线。
“黄线”管制得主题,就是划定重⼤基础设施⽤地影响范围。
1.“红线”管制“红线”概念对于城市各阶层来说都⽐较熟悉。
“红线”划定规划管理部门批准得建设⽤地,主要针对道路控制⽽设⽴,对“红线”得管理体现在对容积率、建设密度与建设⾼度等得规划管理。
“红线”管制得核⼼思想就就是:规划期内得城市建设,必须控制在城市总体规划根据建设⽤地评价确定得⼟地使⽤范围之内;同时城市得具体开发建设,必须在城市建设得建筑“红线”控制范围内与相应得规划要求下进⾏。
“红线”管制⽆论就是技术⽀撑还就是运作程序,在各城市普遍具有⼀定得⼯作基础。
但以成熟得管制制度要求来瞧,需要强化规范性与系统性。
1、1道路“红线”控制对于城市规划确定得规划道路⽤地,尤其就是城市主次⼲道,必须严格按照要求进⾏预留控制。
针对⽬前许多地⽅道路建设盲⽬超前、超规范得“⼤马路情结”,在道路系统及“红线”控制中,必须遵循现阶段得国家有关技术政策,严格执⾏国家《⼯程建设标准强制性条⽂》(城乡规划部分)对不同规模等级城市道路⽹密度、道路宽度等⽅⾯得规定。
表: ⼯程建设标准强制性条⽂关于各类道路宽度得规划指标对于有特殊功能安排得城市道路,必须明确相应得控制要求。
如:为了确保城市特殊情况下抢险救灾、⼈员疏散需要,规划将设定部分城市⼲道为城市内部主要疏散通道,其道路宽度及两侧建筑物⾼度需满⾜以下要求:道路宽度+两侧建筑物后退红线距离≥1/2(H1﹢H2)+4~8⽶。
统筹法计算工程量的方式(三线一面)建筑面积计算基数一、外墙中心线:是指围绕建筑物的外墙中心线长度之和可计算外墙基槽、外墙基础垫层、外墙基础、外墙体积、外墙圈梁、外墙基防潮层二、内墙净长线:是指建筑物内隔墙的长度之和。
可计算内墙基槽、内墙基础垫层、内墙基础、内墙体积、内墙圈梁、内墙基防潮层3、外墙外边线是指建筑物外墙边的长度之和。
人工平整场地、墙脚排水坡、墙脚明沟(阴沟)、外墙脚手架、挑檐4、建筑物底层面积:底层建筑面积。
人工夹带场地、室内回填土、地面垫层、地面面层、顶棚面抹灰、屋面防水卷材、屋面找坡层工程量计算的步骤1.计算“基数”计算工程量时,有些数据常常重复利用,这些数据称为“基数”,包括:1)外墙外边线周长——L外(依照外包尺寸计算)2)外墙中心线长度——L中3)内墙净长线长度——L内(分楼层、墙厚、材质等的不同别离计算,如L内1层370、L内1层240、L内1层120、L内1层60、L内2层240…)4)底层建筑面积——S1(依照建筑面积计算规那么计算1.建筑面积(S建筑面积)和首层建筑面积(S首层建筑面积)❖建筑面积本身也是一些分部份项的计算指标,如脚手架项目、垂直运输项目等,在一样情形下,它们的工程量都为S建筑面积。
S首层建筑面积能够作为平整场地、地面垫层、找平层、面层、防水层等项目工程量的基数,如北京市建筑工程预算定额中,曾经把平整场地的工程量按S=首层建筑面积计算。
2.室内净面积(S室内净面积)❖室内净面积能够作为室内回填土方、地面找平层、垫层、面层和天棚抹灰等的基数。
利用那个基数有两点要注意:一是,若是地面是做块料面层时,地面面层的工程量S应在S室内净面积的基础上,加门口处的块料面积;二是,天棚假设为斜天棚,那么应在室内净面积的基础上乘坡度系数。
3.外墙外边线的长(L外墙外边线)外墙外边线是计算散水、外墙面(裙)装饰、外脚手架等项目的基数。
(1)散水的计算。
按国家预算定额规定的工程量计算规那么,散水是按实际面积计算,若是建筑物的外形是一种非四边形的多边线,而咱们仍按逐块累加的方式计算的话,那么很难计算。
Java基础算法详解查找和排序算法是算法的入门知识,其经典思想可以用于很多算法当中。
因为其实现代码较短,应用较常见。
所以在面试中经常会问到排序算法及其相关的问题。
但万变不离其宗,只要熟悉了思想,灵活运用也不是难事。
一般在面试中最常考的是快速排序和归并排序,并且经常有面试官要求现场写出这两种排序的代码。
对这两种排序的代码一定要信手拈来才行。
还有插入排序、冒泡排序、堆排序、基数排序、桶排序等。
面试官对于这些排序可能会要求比较各自的优劣、各种算法的思想及其使用场景。
还有要会分析算法的时间和空间复杂度。
通常查找和排序算法的考察是面试的开始,如果这些问题回答不好,估计面试官都没有继续面试下去的兴趣都没了。
所以想开个好头就要把常见的排序算法思想及其特点要熟练掌握,有必要时要熟练写出代码。
冒泡排序冒泡排序是最简单的排序之一了,其大体思想就是通过与相邻元素的比较和交换来把小的数交换到最前面。
这个过程类似于水泡向上升一样,因此而得名。
举个栗子,对5,3,8,6,4这个无序序列进行冒泡排序。
首先从后向前冒泡,4和6比较,把4交换到前面,序列变成5,3,8,4,6。
同理4和8交换,变成5,3,4,8,6,3和4无需交换。
5和3交换,变成3,5,4,8,6,3.这样一次冒泡就完了,把最小的数3排到最前面了。
对剩下的序列依次冒泡就会得到一个有序序列。
冒泡排序的时间复杂度为O(n^2)。
实现代码:*@Description:冒泡排序算法实现public class BubbleSort {public static void bubbleSort(int[] arr) {if(arr == null || arr.length == 0)for(int i=0; i) {for(int j=arr.length-1; ji; j--) {if(arr[j]arr[j-1]) {swap(arr, j-1, j);public static void swap(int[] arr, int i, int j) { int temp = arr[i];arr[i] = arr[j];arr[j] = temp;抑或简单理解一点的正向排序public class BubbleSort {public static void bubbleSort(int[] arr) {if(arr == null || arr.length == 0)for(int i=1;iarr.length-1;i++) {for(int j=0; jarr.length-i; j++) {if(arr[j]arr[j+1]) {swap(arr, j+1, j);public static void swap(int[] arr, int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;选择排序选择排序的思想其实和冒泡排序有点类似,都是在一次排序后把最小的元素放到最前面。
但是过程不同,冒泡排序是通过相邻的比较和交换。
而选择排序是通过对整体的选择。
举个栗子,对5,3,8,6,4这个无序序列进行简单选择排序,首先要选择5以外的最小数来和5交换,也就是选择3和5交换,一次排序后就变成了3,5,8,6,4.对剩下的序列一次进行选择和交换,最终就会得到一个有序序列。
其实选择排序可以看成冒泡排序的优化,因为其目的相同,只是选择排序只有在确定了最小数的前提下才进行交换,大大减少了交换的次数。
选择排序的时间复杂度为O(n^2)。
实现代码:*@Description:简单选择排序算法的实现public class SelectSort {public static void selectSort(int[] arr) {if(arr == null || arr.length == 0)int minIndex = 0;for(int i=0; i--只需要比较n-1次minIndex = i;for(int j=i+1; j--从i+1开始比较,因为minIndex默认为i 了,i就没必要比了。
if(arr[j] arr[minIndex]) {minIndex = j;if(minIndex != i) { --如果minIndex不为i,说明找到了更小的值,交换之。
swap(arr, i, minIndex);public static void swap(int[] arr, int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;插入排序插入排序不是通过交换位置而是通过比较找到合适的位置插入元素来达到排序的目的的。
相信大家都有过打扑克牌的经历,特别是牌数较大的。
在分牌时可能要整理自己的牌,牌多的时候怎么整理呢?就是拿到一张牌,找到一个合适的位置插入。
这个原理其实和插入排序是一样的。
举个栗子,对5,3,8,6,4这个无序序列进行简单插入排序,首先假设第一个数的位置时正确的,想一下在拿到第一张牌的时候,没必要整理。
然后3要插到5前面,把5后移一位,变成3,5,8,6,4.想一下整理牌的时候应该也是这样吧。
然后8不用动,6插在8前面,8后移一位,4插在5前面,从5开始都向后移一位。
注意在插入一个数的时候要保证这个数前面的数已经有序。
简单插入排序的时间复杂度也是O(n^2)。
实现代码:*@Description:简单插入排序算法实现public class InsertSort {public static void insertSort(int[] arr) {if(arr == null || arr.length == 0)for(int i=1; i--假设第一个数位置时正确的;要往后移,必须要假设第一个。
int target = arr[i]; --待插入的while(j 0 target ]) {arr[j] = arr[j-1];arr[j] = target;快速排序快速排序一听名字就觉得很高端,在实际应用当中快速排序确实也是表现最好的排序算法。
快速排序虽然高端,但其实其思想是来自冒泡排序,冒泡排序是通过相邻元素的比较和交换把最小的冒泡到最顶端,而快速排序是比较和交换小数和大数,这样一来不仅把小数冒泡到上面同时也把大数沉到下面。
举个栗子:对5,3,8,6,4这个无序序列进行快速排序,思路是右指针找比基准数小的,左指针找比基准数大的,交换之。
5,3,8,6,4 用5作为比较的基准,最终会把5小的移动到5的左边,比5大的移动到5的右边。
5,3,8,6,4 首先设置i,j两个指针分别指向两端,j指针先扫描(思考一下为什么?)4比5小停止。
然后i扫描,8比5大停止。
交换i,j位置。
5,3,4,6,8 然后j指针再扫描,这时j扫描4时两指针相遇。
停止。
然后交换4和基准数。
4,3,5,6,8 一次划分后达到了左边比5小,右边比5大的目的。
之后对左右子序列递归排序,最终得到有序序列。
上面留下来了一个问题为什么一定要j指针先动呢?首先这也不是绝对的,这取决于基准数的位置,因为在最后两个指针相遇的时候,要交换基准数到相遇的位置。
一般选取第一个数作为基准数,那么就是在左边,所以最后相遇的数要和基准数交换,那么相遇的数一定要比基准数小。
所以j指针先移动才能先找到比基准数小的数。
快速排序是不稳定的,其时间平均时间复杂度是O(nlgn)。
实现代码:*@Description:实现快速排序算法public class QuickSort {--一次划分public static int partition(int[] arr, int left, int right) {int pivotKey = arr[left];int pivotPointer = left;while(left right) {while(left = pivotKey)right --;while(left pivotKey)swap(arr, left, right); --把大的交换到右边,把小的交换到左边。
swap(arr, pivotPointer, left); --最后把pivot交换到中间 return left;public static void quickSort(int[] arr, int left, int right) {if(left = right)int pivotPos = partition(arr, left, right);quickSort(arr, left, pivotPos-1);quickSort(arr, pivotPos+1, right);public static void sort(int[] arr) {if(arr == null || arr.length == 0)quickSort(arr, 0, arr.length-1);public static void swap(int[] arr, int left, int right) { int temp = arr[left];arr[left] = arr[right];arr[right] = temp;其实上面的代码还可以再优化,上面代码中基准数已经在pivotKey中保存了,所以不需要每次交换都设置一个temp变量,在交换左右指针的时候只需要先后覆盖就可以了。
这样既能减少空间的使用还能降低赋值运算的次数。
优化代码如下:*@Description:实现快速排序算法public class QuickSort {* @param arr* @param left* @param right* @returnpublic static int partition(int[] arr, int left, int right) {int pivotKey = arr[left];while(left right) {while(left = pivotKey)right --;arr[left] = arr[right]; --把小的移动到左边while(left pivotKey)arr[right] = arr[left]; --把大的移动到右边arr[left] = pivotKey; --最后把pivot赋值到中间return left;* 递归划分子序列* @param arr* @param left* @param rightpublic static void quickSort(int[] arr, int left, int right) {if(left = right)int pivotPos = partition(arr, left, right);quickSort(arr, left, pivotPos-1);quickSort(arr, pivotPos+1, right);public static void sort(int[] arr) {if(arr == null || arr.length == 0)quickSort(arr, 0, arr.length-1);总结快速排序的思想:冒泡+二分+递归分治,慢慢体会。