线性规划问题及其数学模型
- 格式：doc
- 大小：175.00 KB
- 文档页数：6
下载文档原格式
合集下载
第一章线性规划-模型和图解法
a22 am2
a1n
a2n amn
(P1,
P2 ,
, Pn )
用向量表示时，上述模型可写为：
max(min)Z CX
s.t
n j 1
Pj x j
(, )b
X 0
线性规划问题可记为矩阵和向量的形式：
max(min)Z CX
s.t
AX
X
(, )b 0
max(min)Z CX
x21 x23
x14
x23
x32
x41
xij 0(i 1, ,4;
15
x22 x31 12
x23 x32
j 1, ,4)
10 20
二。线性规划问题的数学模型 下面从数学的角度来归纳上述三个例子的共同点。 ①每一个问题都有一组变量---称为决策变量，一般记为
x1, x2 , , xn. 对决策变量每一组值：(x1(0) , x2(0) , xn(0) )T 代表了
表1-3
月份
12
所需仓库面积 15 10
单位：100m2
34 20 12
合同租借期限 合同期内的租费
表1-4
单位；元/100m2
1个月 2个月 3个月 4个月
2800 4500 6000 7300
表1-2
月份
12
所需仓库面积 15 10
单位：100m2
34 20 12
合同租借期限 合同期内的租费
max(min) Z c1x1 c2 x2 cn xn
a11x1 a12 x2 a1n xn (, )b1
s.t
a21x1
a22 x2
a2n xn
(, )b2
am1x1 am2 x2 amnxn (, )bm
线性规划
• 4.2 两阶段法
• 两阶段法是处理人工变量的另一种方法。其具体做 法是在原约束条件中增加人工变量，构造一个新的 目标函数，其中人工变量的系数为-1，其余变量的 系数为0，这样就产生了如下的最优解有三种情形。 （1）这说明在辅助问题的最优解中，还有人工变量是基变量， 且取值不为0，此时原问题无可行解。 （2）且最优解中人工变量均为非基变量，则把它们划去后就得 到了原问题的一个基本可行解。 （3）但最优解中还有人工变量是基变量，其取值为0。这时， 只要选某个不是人工变量的非基变量进基，把在基中的人工 变量替换出来，则情形同（2）。 第二阶段：对于第一阶段的后两种情形，在第一阶段的最优单 纯形表中划去人工变量所在的列，并把检验数行换成原问题 目标函数（消去基变量以后）的系数，从而得到原问题的初 始单纯形表，再继续迭代求解。
2014-6-19 3
例2（运输问题）
• 设有某种物资要从A1，A2，A3三个仓库运往四个 销售点B1，B2，B3，B4。各发点（仓库）的发货 量、各收点（销售点）的收货量以及 到 的单位运 费如表1-2。问如何组织运输才能使总运费最少？
例3（配料问题）
• 在现代化的大型畜牧业中，经常使用工业生产的饲料。 设某种饲料由四种原料B1，B2，B3 ，B4混合而成，要 求它含有三种成份（如维生素、抗菌素等）A1，A2， A3的數量分別不少于25、36、40个单位（这些单位可 以互不相同），各种原料的每百公斤中含三种成份的数 量及各种原料的单价如表1-3.
1.2 线性规划的数学模型
一、一般形式 上述各例具有下列共同特征： 1．存在一组变量 ，称为决策变量，表示某一方案。通 常要求这些变量的取值是非负的。 2．存在若干个约束条件，可以用一组线性等式或线性 不等式来描述。 3．存在一个线性目标函数，按实际问题求最大值或最 小值。
第1章 线性规划
投资项目 1 2 3 4 5 6 风险（%） 18 6 10 4 12 8 红利（%） 4 5 9 7 6 8 增长（%） 22 7 12 8 15 8 信用度 4 10 2 10 4 6
1.1 线性规划问题及其数学模型
线性规划
该公司想达到的目标为：投资 风险最小，每年红利至少为6.5万 元，最低平均增长率为12%，最低 平均信用度为7。请用线性规划方 法求解该问题。
1.1 线性规划问题及其数学模型
解：
（1）决策变量
线性规划
本问题的决策变量是在每种投资项目上的投 资 额 。 设 xi 为 项 目 i 的 投 资 额 （ 万 元 ） （ i=1,2,,6）
（2）目标函数
本问题的目标为总投资风险最小，即
Min z 0.18x1 0.06x2 0.10x3 0.04x4 0.12x5 0.08x6
线性规划
运筹学
线性规划
线性规划
本章内容要点
线性规划问题及其数学模型；
线性规划的电子表格建模； 线性规划的多解分析。
线性规划
本章内容
1.1 线性规划问题及其数学模型
1.2 线性规划问题的图解法
1.3 用Excel“规划求解”功能求解线性规划问题
1.4 线性规划问题求解的几种可能结果
本章主要内容框架图
1.4 线性规划问题求解的 几种可能结果
线性规划
唯一解 无穷多解 无解 可行域无界（目标值不收敛）
1.4 线性规划问题求解的 几种可能结果
线性规划
唯一解
线性规划问题具有 唯一解是指该规划 问题有且仅有一个 既在可行域内、又 使目标值达到最优 的解。例1.1就是一 个具有唯一解的规 划问题
(1-1)
1.1 线性规划问题及其数学模型
线性规划
该公司想达到的目标为：投资 风险最小，每年红利至少为6.5万 元，最低平均增长率为12%，最低 平均信用度为7。请用线性规划方 法求解该问题。
1.1 线性规划问题及其数学模型
解：
（1）决策变量
线性规划
本问题的决策变量是在每种投资项目上的投 资 额 。 设 xi 为 项 目 i 的 投 资 额 （ 万 元 ） （ i=1,2,,6）
（2）目标函数
本问题的目标为总投资风险最小，即
Min z 0.18x1 0.06x2 0.10x3 0.04x4 0.12x5 0.08x6
线性规划
运筹学
线性规划
线性规划
本章内容要点
线性规划问题及其数学模型；
线性规划的电子表格建模； 线性规划的多解分析。
线性规划
本章内容
1.1 线性规划问题及其数学模型
1.2 线性规划问题的图解法
1.3 用Excel“规划求解”功能求解线性规划问题
1.4 线性规划问题求解的几种可能结果
本章主要内容框架图
1.4 线性规划问题求解的 几种可能结果
线性规划
唯一解 无穷多解 无解 可行域无界（目标值不收敛）
1.4 线性规划问题求解的 几种可能结果
线性规划
唯一解
线性规划问题具有 唯一解是指该规划 问题有且仅有一个 既在可行域内、又 使目标值达到最优 的解。例1.1就是一 个具有唯一解的规 划问题
(1-1)
线性规划的数学模型
线性规划的数学模型引言线性规划（Linear Programming, LP）是数学规划的一种方法，用于解决一类特殊的优化问题。
线性规划的数学模型可以表示为一个线性的目标函数和一系列线性约束条件。
本文将介绍线性规划的数学模型及其应用。
数学模型线性规划的数学模型可以用以下形式表示：最大化：$$ \\max_{x_1,x_2,...,x_n} Z=c_1x_1+c_2x_2+...+c_nx_n $$约束条件：$$ \\begin{align*} a_{11}x_1+a_{12}x_2+...+a_{1n}x_n&\\leq b_1 \\\\ a_{21}x_1+a_{22}x_2+...+a_{2n}x_n &\\leq b_2 \\\\ &\\vdots \\\\ a_{m1}x_1+a_{m2}x_2+...+a_{mn}x_n&\\leq b_m \\\\ x_1,x_2,...,x_n &\\geq 0 \\end{align*} $$其中，Z为目标函数的值，Z1,Z2,...,Z Z为目标函数的系数，Z1,Z2,...,Z Z为决策变量，Z ZZ为约束条件的系数，Z1,Z2,...,Z Z为约束条件的右侧常数。
线性规划的应用线性规划在实际问题中有广泛的应用，其应用领域包括但不限于以下几个方面：生产计划线性规划在生产计划中的应用是最为常见的。
通过建立适当的数学模型，可以最大化生产线的产能，同时满足客户需求和资源限制。
例如，一个工厂需要决定每个月生产的产品数量，以最大化利润。
这个问题可以通过线性规划来解决。
运输问题线性规划在运输问题中的应用也非常广泛。
运输问题涉及到将特定产品从供应地点运送到需求地点，以满足需求并尽量降低运输成本。
线性规划可以用来决定每个供应地点到每个需求地点的运输量，以最小化总运输成本。
资源分配在资源有限的情况下，线性规划可以用于优化资源的分配。
线性规划问题及其数学模型
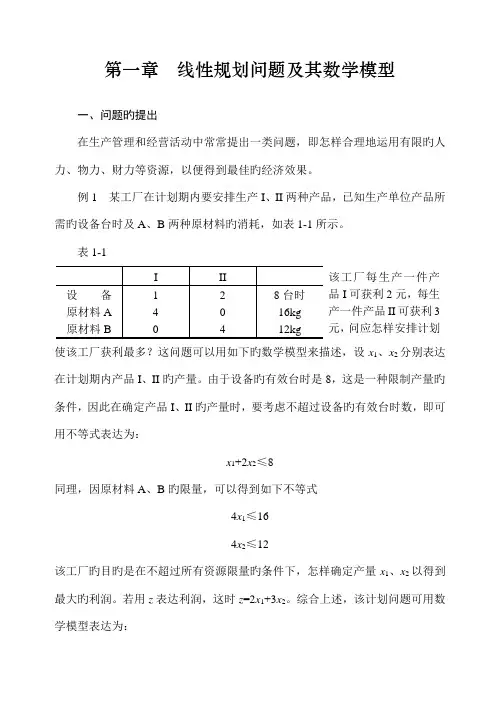
第一章线性规划问题及其数学模型一、问题旳提出在生产管理和经营活动中常常提出一类问题，即怎样合理地运用有限旳人力、物力、财力等资源，以便得到最佳旳经济效果。
例1 某工厂在计划期内要安排生产I、II两种产品，已知生产单位产品所需旳设备台时及A、B两种原材料旳消耗，如表1-1所示。
表1-1该工厂每生产一件产品I可获利2元，每生产一件产品II可获利3元，问应怎样安排计划使该工厂获利最多？这问题可以用如下旳数学模型来描述，设x1、x2分别表达在计划期内产品I、II旳产量。
由于设备旳有效台时是8，这是一种限制产量旳条件，因此在确定产品I、II旳产量时，要考虑不超过设备旳有效台时数，即可用不等式表达为：x1+2x2≤8同理，因原材料A、B旳限量，可以得到如下不等式4x1≤164x2≤12该工厂旳目旳是在不超过所有资源限量旳条件下，怎样确定产量x1、x2以得到最大旳利润。
若用z表达利润，这时z=2x1+3x2。
综合上述，该计划问题可用数学模型表达为：目旳函数 max z =2x 1+3x 2 满足约束条件 x 1+2x 2≤84x 1≤16 4x 2≤12 x 1、x 2≥0例2 某铁路制冰厂每年1至4季度必须给冷藏车提供冰各为15，20，25，10kt 。
已知该厂各季度冰旳生产能力及冰旳单位成本如表6-26所示。
假如生产出来旳冰不在当季度使用，每千吨冰存贮一种季度需存贮费4千元。
又设该制冰厂每年第3季度末对贮冰库进行清库维修。
问应怎样安排冰旳生产，可使该厂整年生产费用至少？解：由于每个季度生产出来旳冰不一定当季度使用，设x ij 为第i 季度生产旳用于第j 季度旳冰旳数量。
按照各季度冷藏车对冰旳需要量，必须满足：⎪⎪⎩⎪⎪⎨⎧++++++33231343221242114144x x x x x x x x x x 。
，，，25201510==== 又每个季度生产旳用于当季度和后来各季度旳冰旳数量不也许超过该季度旳生产能力，故又有⎪⎪⎩⎪⎪⎨⎧++++++33232213121143424144x x x x x x x x x x 。
第1章-线性规划模型-宋
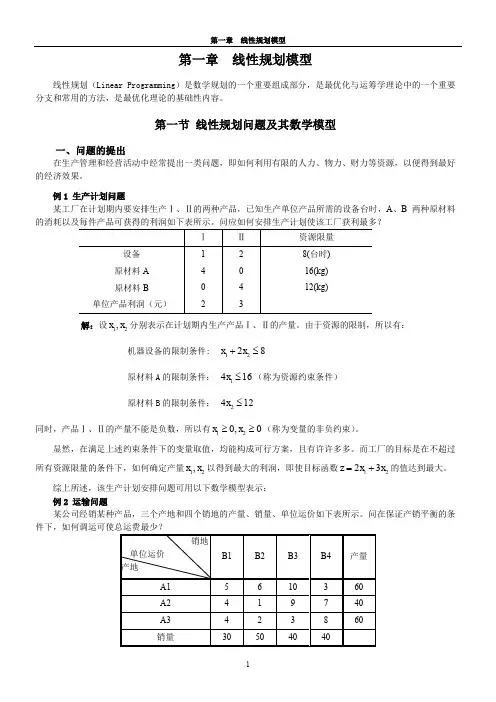
第一章 线性规划模型线性规划（Linear Programming ）是数学规划的一个重要组成部分，是最优化与运筹学理论中的一个重要分支和常用的方法，是最优化理论的基础性内容。
第一节 线性规划问题及其数学模型一、问题的提出在生产管理和经营活动中经常提出一类问题，即如何利用有限的人力、物力、财力等资源，以便得到最好的经济效果。
例1 生产计划问题某工厂在计划期内要安排生产Ⅰ、Ⅱ的两种产品，已知生产单位产品所需的设备台时，A 、B 两种原材料的消耗以及每件产品可获得的利润如下表所示。
问应如何安排生产计划使该工厂获利最多？解：设12,x x 分别表示在计划期内生产产品Ⅰ、Ⅱ的产量。
由于资源的限制，所以有：机器设备的限制条件: 1228x x +≤原材料A 的限制条件： 1416x ≤（称为资源约束条件） 原材料B 的限制条件： 2412x ≤同时，产品Ⅰ、Ⅱ的产量不能是负数，所以有120,0x x ≥≥（称为变量的非负约束）。
显然，在满足上述约束条件下的变量取值，均能构成可行方案，且有许许多多。
而工厂的目标是在不超过所有资源限量的条件下，如何确定产量12,x x 以得到最大的利润，即使目标函数1223z x x =+的值达到最大。
综上所述，该生产计划安排问题可用以下数学模型表示：例2 运输问题某公司经销某种产品，三个产地和四个销地的产量、销量、单位运价如下表所示。
问在保证产销平衡的条解:（1）决策变量：设(1,2,3;1,2,3,4)ij x i j ==为从产地i 运到销地j 的运量（2）目标函数：总运费最小3411min ij iji j z c x===∑∑（3）约束条件： 产量约束 销量约束 非负约束 模型为：二、线性规划问题的模型上述几例所提出的问题，可归结为在变量满足线性约束条件下，求使线性目标函数值最大或最小的问题。
它们具有以下共同的特征。
（1）每个问题都可用一组决策变量12(,,,)n x x x 表示某一方案，其具体的值就代表一个具体方案。
线性规划-讲义-12章
第一章 线性规划 第二章 对偶单纯形法与灵敏度分析 第三章 运输问题 第四章
整数规划
第五章 动态规划
第六章 图论与问题及其数学模型 1.1.1 线性规划问题的数学模型
例1、生产计划问题 I 1 3 0 40 II 2 2 2 50
原材料A 原材料B 台时 利润
例6 max S=2x1+ 4x2 2x1+x2 8
x2
8
-2x1+ x2=2
-2x1+x2 2
x1 , x2 0 无界解(无最优解) 无界解=>可行域无界 <=
6
4
2
0
4
x1
2x1+ x2=8
例7 max S=3x1+2x2 -x1 -x2 1
x1 , x2 0 有解 无可行解 唯一解 无穷多解 无有限最优解 无可行解
(3) 变量 若xj 0, 令 xj = -xjˊ, 其中: xjˊ 0 若xj是无限制变量. 令 xj = xjˊ- xj〞, 其中: xjˊ、 xj〞 0
例 3x1+2x2 8
x1 –4x2 14
x2 0 令x1= x1'- x1 " 3 x1' –3x1 " +2x2 8 x1' - x1 " – 4x2 14 x1' , x1" ,x2 0
2x3 +2x4+ x5=100 3x1+ x2+2x3 +3x5=100
xi 0 (i =1,…,5)，且为整数
最优方案是：按方案I-30根, II-10根；III-50根 即只要90根原料--制造100套
运输问题
整数规划
第五章 动态规划
第六章 图论与问题及其数学模型 1.1.1 线性规划问题的数学模型
例1、生产计划问题 I 1 3 0 40 II 2 2 2 50
原材料A 原材料B 台时 利润
例6 max S=2x1+ 4x2 2x1+x2 8
x2
8
-2x1+ x2=2
-2x1+x2 2
x1 , x2 0 无界解(无最优解) 无界解=>可行域无界 <=
6
4
2
0
4
x1
2x1+ x2=8
例7 max S=3x1+2x2 -x1 -x2 1
x1 , x2 0 有解 无可行解 唯一解 无穷多解 无有限最优解 无可行解
(3) 变量 若xj 0, 令 xj = -xjˊ, 其中: xjˊ 0 若xj是无限制变量. 令 xj = xjˊ- xj〞, 其中: xjˊ、 xj〞 0
例 3x1+2x2 8
x1 –4x2 14
x2 0 令x1= x1'- x1 " 3 x1' –3x1 " +2x2 8 x1' - x1 " – 4x2 14 x1' , x1" ,x2 0
2x3 +2x4+ x5=100 3x1+ x2+2x3 +3x5=100
xi 0 (i =1,…,5)，且为整数
最优方案是：按方案I-30根, II-10根；III-50根 即只要90根原料--制造100套
运输问题
1.1 72线性规划问题及其数学模型
可行域
4 3 2
最优解
8 0 3 4
x1
无穷多最优解(多重最优解)
即可行域的范围延伸到无 例： max z=x1+x2
穷远，目标函数值可以无 穷大或无穷小。 ≤4 s.t. -2x1+ x2 一般来说，这说明模型有 x1 - x2 ≤2 错，忽略了一些必要的约 束条件。 ≥0, x2≥0 x1 x2
无穷 多个最优解
2.可行域为非封闭的无界区域
x2 x2 x2
z
z
x1 x1
Z
x1
唯一最优解
无穷多个最优解
无界解
3、可行域为空集
x2
空集 x1
无可行解
两个变量的LP问题的解的启示：
(1)可行域非空时，它是有界或无界凸多边形 （凸集） ，顶点个数只有有限个。 (2)求解LP问题时，解的情况有： 唯一最优解；无穷多最优解；无界解；无可行解。 (3)若可行域非空且有界则必有最优解， 若可行域无界，则可能有最优解，也可能无最优解。 (4)若最优解存在，则最优解或最优解之一一定是 可行域的凸集的某个顶点。 (5)若在两个顶点上同时取到最优解，则这两点的 连线上 任一点都是最优解
由图解法得到的结论：
求解线性规划问题最优解的方法：
确定可行域 = 凸集(凸多边形) 确定可行域顶点 = 求基可行解 寻找最优解， 如果最优解存在，则必在可行域的某一顶点 = 在基可行解中寻找
图解法优点： 直观、易掌握。有助于了解解的结构。
图解法缺点：
只能解决低维问题，对高维无能为力。
1.3 线性规划问题的标准型式
m i nZ
C
j 1
n j1
n
j
Xj
4 3 2
最优解
8 0 3 4
x1
无穷多最优解(多重最优解)
即可行域的范围延伸到无 例： max z=x1+x2
穷远，目标函数值可以无 穷大或无穷小。 ≤4 s.t. -2x1+ x2 一般来说，这说明模型有 x1 - x2 ≤2 错，忽略了一些必要的约 束条件。 ≥0, x2≥0 x1 x2
无穷 多个最优解
2.可行域为非封闭的无界区域
x2 x2 x2
z
z
x1 x1
Z
x1
唯一最优解
无穷多个最优解
无界解
3、可行域为空集
x2
空集 x1
无可行解
两个变量的LP问题的解的启示：
(1)可行域非空时，它是有界或无界凸多边形 （凸集） ，顶点个数只有有限个。 (2)求解LP问题时，解的情况有： 唯一最优解；无穷多最优解；无界解；无可行解。 (3)若可行域非空且有界则必有最优解， 若可行域无界，则可能有最优解，也可能无最优解。 (4)若最优解存在，则最优解或最优解之一一定是 可行域的凸集的某个顶点。 (5)若在两个顶点上同时取到最优解，则这两点的 连线上 任一点都是最优解
由图解法得到的结论：
求解线性规划问题最优解的方法：
确定可行域 = 凸集(凸多边形) 确定可行域顶点 = 求基可行解 寻找最优解， 如果最优解存在，则必在可行域的某一顶点 = 在基可行解中寻找
图解法优点： 直观、易掌握。有助于了解解的结构。
图解法缺点：
只能解决低维问题，对高维无能为力。
1.3 线性规划问题的标准型式
m i nZ
C
j 1
n j1
n
j
Xj
线性规划
1.3 线性规划问题的标准型式
M1 : 目标函数： max z c 1 x 1 c 2 x 2 c n x n a 11 x 1 a 12 x 2 a 1 n x n b1 a x a 22 x 2 a 2 n x n b 2 21 1 约束条件： a x a x a x b m2 2 mn n n m1 1 x 1 , x 2 , , x n 0
24
第2节 应用举例
最终计算表（第3次计算）
c j→ CB 0.1 -0.3 0 XB x2 x4 x1 c j -z j b 10 50 30 0 x1 0 0 1 0 0.1 x2 1 0 0 0 0.2 x3 -1 1 1 0 0.3 x4 0 1 0 0 0.8 x5 -9/10 1/3 13/10 -0.74 -M x6 3/5 0 -1/5 -M + 0.06 -M x7 -3/10 1/3 1/10 -M + 0.12 -M x8 -1/5 0 2/5 -M -0.02 θ
27
第2节 应用举例
表1-7表明这些原材料供应数量的限额。加入到产品A、 B、D的原材料C总量每天不超过100kg，P的总量不超过 100kg，H总量不超过60kg。
表1-7
原材料名称 C P H 每 天 最 多 供 应 量 （ kg） 100 100 60 单 价 /(元 /kg) 65 25 35
29
第2节 应用举例
约束条件可表示为：
1 2 1 4 x1 x1 1 2 3 4 x2 x2 1 2 1 4 x3 x3 x1 x2 x3 x1 , , x 9 0 3 4 1 2 x4 x4 1 4 1 2 x5 x5 1 4 1 2 x6 x6 x7 x5 x6 x8 0 0 0 0 100 100 x 9 60
M1 : 目标函数： max z c 1 x 1 c 2 x 2 c n x n a 11 x 1 a 12 x 2 a 1 n x n b1 a x a 22 x 2 a 2 n x n b 2 21 1 约束条件： a x a x a x b m2 2 mn n n m1 1 x 1 , x 2 , , x n 0
24
第2节 应用举例
最终计算表（第3次计算）
c j→ CB 0.1 -0.3 0 XB x2 x4 x1 c j -z j b 10 50 30 0 x1 0 0 1 0 0.1 x2 1 0 0 0 0.2 x3 -1 1 1 0 0.3 x4 0 1 0 0 0.8 x5 -9/10 1/3 13/10 -0.74 -M x6 3/5 0 -1/5 -M + 0.06 -M x7 -3/10 1/3 1/10 -M + 0.12 -M x8 -1/5 0 2/5 -M -0.02 θ
27
第2节 应用举例
表1-7表明这些原材料供应数量的限额。加入到产品A、 B、D的原材料C总量每天不超过100kg，P的总量不超过 100kg，H总量不超过60kg。
表1-7
原材料名称 C P H 每 天 最 多 供 应 量 （ kg） 100 100 60 单 价 /(元 /kg) 65 25 35
29
第2节 应用举例
约束条件可表示为：
1 2 1 4 x1 x1 1 2 3 4 x2 x2 1 2 1 4 x3 x3 x1 x2 x3 x1 , , x 9 0 3 4 1 2 x4 x4 1 4 1 2 x5 x5 1 4 1 2 x6 x6 x7 x5 x6 x8 0 0 0 0 100 100 x 9 60
线性规划问题的数学模型
工地 砖厂
运价
A1
A2
B1
B2
B3
50
60
70
60
110
160
在线才智在线才智在线才智在线才
智在线才智
2
解：设 xi j表示由砖厂Ai 运往工地 Bj 砖的数量（i=1,2； j=1,2,3)
运量
工
地
B1
B2
B3
发量
砖厂
A1
x11
x12
x13
23
A2
x21
x22
x23
27
收量 17 18 15 50
⑵ 存在一定的限制条件，称为约束条件。这些约束条件 都可以用一组线性等式或不等式来表示。
⑶ 都有一个期望达到的目标，并且这个目标可以表示为 决策变量的线性函数（称为目标函数）。按所研究问题的不 同，要求目标函数值最大化或最小化。
我们将具有上述三个特点的最优化问题归结为线性规划问
题，其数学模型称为线性规划问题的数学模型，简称线性规划 数学模型。
智在线才智
15
解：
x2 x1 + x2 = -2
x1
-x1 + x2 =1
没有可行解，当然没有最优解。
在线才智在线才智在线才智在线才
智在线才智
16
第三节 单纯形法
（一）线性规划问题的标准形式
线性规划问题的数学模型有各种不同的形式。为了便于讨论，需要将线性 规划数学模型写成统一格式。
线性规划问题的标准型是：
4.配料问题
5.布局问题
6.分配问题
在线才智在线才智在线才智在线才
智在线才智
1
（二）线性规划问题的数学模型
线性规划概念与数学模型
约束条件的图解:
每一个约束不等式在平面直角坐标系中都 代表一个半平面，只要先画出该半平面的边 界，然后确定是哪个半平面。
怎么画边界
?
怎么确定 半平面
以第一个约束条件（工时）
x1+2 x2 8 为例 说明约束条件的图解过程。
如果全部的劳动工时都用来生产甲 产品而不生产
乙产品，那么甲产品的最大可能产量为8吨，计算
D
条件的边界－－
4
Q4
Q3
直线CD，EF: E
3
F
4x1 =16,4x2 =12
2
Q2 4x2 = 12
1
Q1
0
1
2
3
4
5
6
7
8
9
B
C
x1+4x2 = 8
4x1=16
三个约束条件及非负条件x1,x2 0所代表的公共部分
－－图中阴影区，就是满足所有约束条件和非负条件的点的
集合，即可行域。在这个区域中的每一个点都对应着一个可
目标函数值递增的方向， 用箭头标出这个方向。 图中两条虚线 l1和l2就 分别代表 目标函数等值线 2x1+3x2=0 和 2x1+3x2=6, 箭头表示使两种产品的总 利润递增的方向。
5
l3
A4
E
B
3
l1 l2 2
1
1
2
D
F 4x1=12
Q2 4,2
x1+2x2 = 8
A
3
4
5
6
7
8
9
B
4x1=16 C
1 1
1 1
1 1
B1 1
4 , B2 1
线性规划问题及其数学模型
6
例 ： min z x1 2 x2 3x3
x1
x2 x3 7 x7
x1
x2 x3 2
3x1 x2 2 x3 7
x1, x2 0, x3无约x束 3 x4 x5
上页 下页 返回
解 ：标准形为
max z x1 2x2 3(x4 x5 ) 0x6 0x7
供需平衡
上页 下页 返回
线性规划模型举例
(一) 运输问题 (二) 布局问题 (三) 分派问题 (四) 生产计划问题 (五) 合理下料问题
上页 下页 返回
线性规划模型的条件
• （1）要求解问题的目标函数能用数 值指标来反映，且为线性函数；
• （2）存在着多种方案； • （3）要求达到的目标是在一定约束
• “” 约束：加入非负松驰变量
例： max z 2x1 3x2 0x3 0x4 0x5
x1 2x2 x3
8
4
x1
4 x2
x4 16 x5 12
x1, x2 , x3, x4 , x5 0
上页 下页 返回
• “” 约束： 减去非负剩余变量；
• xk可正可负（即无约束）；
x 令 xk Mxak' x xk" xk' , xk" 0
i 1
每人只做一件工作
n xij 1
每人i 对每1,件2工,作只, n有
j 1
做与不做两种情况
xij 0 或 1 i, j 1,2,, n
上页 下页 返回
(四）生产组织与计划问题
(Ⅰ) 生产的机器最多 (Ⅱ) 总的加工成本最低 （Ⅲ）生产存储问题
上页 下页 返回
(四）生产组织与计划问题 应如何分配机
线性规划问题及其数学模型
设 Q 为第i处设厂的规模，即年产产品数量（万吨），则有
i
Q 1 = y 11 + y 12 , Q 2 = y 21 + y 22 , Q 3 = y 31 + y 32
据每吨产品需3吨原料，有 （生产的产品全部+ x 31 = 3 ( y 11 + y 12 )
)
例8：厂址选择问题 甲、乙、丙三地，每地都生产一定数量的原料，也消耗一定 数量的产品（如下表）。已知制成每吨产品需3吨原料，各地之 间的距离为：甲—乙，150千米；甲—丙，100千米；乙—丙， 200千米。假定每万吨原料运输1千米的运价为5000元，每万吨 产品运输1千米的运价为6000元。由于地区差异，在不同地点设 厂的生产费用也不同。试问究竟在哪些地方设厂，规模多大， 才能使总费用最小？另外，由于其他条件限制，在乙处建厂的 规模（生产的产品数量）不能超过5万吨
解：设xij为第i年投资到第j个方向的资金
第一年年初： 第二年年初： 第三年年初： 第三年底：
x11 + x12 = 3
x12 ≤ 2 x23 ≤ 1.5 x34 ≤ 1
x21 + x23 = 1.2 x11
x31 + x34 = 1.5x12 +1.2x21
z = 1.6 x23 + 1.2 x31 + 1.4 x34
2 x2 + x3 + 3x5 + 2 x6 + x7 = 10000 x1 + x3 + 3x4 + 2 x6 + 3x7 + 4 x8 = 10000
x j ≥ 0 . j = 1, 2 , 3 , K ,8
例6：某厂在今后四个月内需租用仓库堆存货物。已知各个月所需 的仓库面积数如表1所示。又知，当租借合同期限越长时，场地租 借费用享受的折扣优待越大，有关数据如表2所示。租借仓库的合 同每月初都可办理，每份合同应具体说明租借的场地面积数和租借 期限。工厂在任何一个月初办理签约时，可签一份，也可同时签若 干份租借场地面积数和租借期限不同的合同。为使所付的场地总租 借费用最少，试建立一个线性规划模型。
线性规划问题及其数学模型
就代表一个具体方案一般这些变量取值是非负 且连续的；
2要有各种资源和使用有关资源的技术数据 创造新价值的数据；
a i; jcj(i1 , m ;j1 , n)
共同的特征继续
3 存在可以量化的约束条件这些约束条件可 以用一组线性等式或线性不等式来表示;
4 要有一个达到目标的要求它可用决策变量 的线性函数称为目标函数来表示按问题的 不同要求目标函数实现最大化或最小化
约束条件：
a
21
x1
a22
x
2
a2n xn
b2
a
m
1
x1
am 2 x2
a mn xn
bn
x1 , x2 , , xn 0
线性规划问题的几种表示形式
M
' 1
:
n
目标函数：max z c j x j
j 1
约束条件：
n
aij x j
j 1
bi ,
i 1,2, ,m
x
j
0,
j 1,2, ,n
弛变量x6； 3 在第二个约束不等式≥号的左端减去剩
余变量x7； 4 令z′= -z把求min z 改为求max z′即可得到
该问题的标准型
例4的标准型
max z ' x1 2 x 2 3( x 4 x5 ) 0 x6 0 x7
x1 x2 ( x4 x5 ) x6
7
x1 x2 ( x4 x5 )
经第2工厂后的水质要求：
[0.8(2x1)(1.4x2 )] 2
700
1000
数学模型
目标函数 约束条件
min z 1000 x1 800 x2 x1 1
0.8 x1 x2 1.6 x1 2 x2 1.4 x1 , x2 0
2要有各种资源和使用有关资源的技术数据 创造新价值的数据；
a i; jcj(i1 , m ;j1 , n)
共同的特征继续
3 存在可以量化的约束条件这些约束条件可 以用一组线性等式或线性不等式来表示;
4 要有一个达到目标的要求它可用决策变量 的线性函数称为目标函数来表示按问题的 不同要求目标函数实现最大化或最小化
约束条件：
a
21
x1
a22
x
2
a2n xn
b2
a
m
1
x1
am 2 x2
a mn xn
bn
x1 , x2 , , xn 0
线性规划问题的几种表示形式
M
' 1
:
n
目标函数：max z c j x j
j 1
约束条件：
n
aij x j
j 1
bi ,
i 1,2, ,m
x
j
0,
j 1,2, ,n
弛变量x6； 3 在第二个约束不等式≥号的左端减去剩
余变量x7； 4 令z′= -z把求min z 改为求max z′即可得到
该问题的标准型
例4的标准型
max z ' x1 2 x 2 3( x 4 x5 ) 0 x6 0 x7
x1 x2 ( x4 x5 ) x6
7
x1 x2 ( x4 x5 )
经第2工厂后的水质要求：
[0.8(2x1)(1.4x2 )] 2
700
1000
数学模型
目标函数 约束条件
min z 1000 x1 800 x2 x1 1
0.8 x1 x2 1.6 x1 2 x2 1.4 x1 , x2 0
第一章 线性规划
对于标准形式的线性规划问题若约束方程系数矩阵中不存在现成的初始可行基则不能简单的用上述单纯形法而通常采用所谓的人工变量法
第一章 线性规划
(Linear Programming, LP)
概述
• 线性规划问题的提出最早是1939年由前苏联 数学家康托洛维奇在研究铁路运输的组织问题、 工业生产的管理问题时提出来的。
（5）若bi < 0，则－bi > 0
举例: 化下列线性规划为标准形
max z=2x1+2x2－4x3 x1 + 3x2－3x3 ≥30 x1 + 2x2－4x3≤80 x1、x2≥0，x3无限制
max z=2x1+2x2－4x3’+4x3” x1 + 3x2－3x3’+3x3” –x4 = 30 x1 + 2x2－4x3+ 4x3” + x5 = 80 x1、x2 、x3’、x3” 、x4、x5 ≥0
称X0为该线性规划对应与基B的一个基本解。
同样，在A中任选m个线性无关的列向量都可以组成一个基， 对应基一个基本解。对于一个LP最多有多少呢？从n个中 选m个进行组合，即：
Cnm=n！/[（n－m）！m！] 因此，基本解是有限的。
举例：找出下列LP所有的基及其对应的基本解 max z=6x1+4x2 2x1 + 3x2≤100 4x1 + 2x2≤120 x1、x2≥0
资源
产品
甲
乙 资源限制
A
1
B
2
C
0
单位产品利润(元/件) 50
1
300kg
1
400kg
1
250kg
100
• 决策变量：x1、x2——分别代表甲、乙两
第一章 线性规划
(Linear Programming, LP)
概述
• 线性规划问题的提出最早是1939年由前苏联 数学家康托洛维奇在研究铁路运输的组织问题、 工业生产的管理问题时提出来的。
（5）若bi < 0，则－bi > 0
举例: 化下列线性规划为标准形
max z=2x1+2x2－4x3 x1 + 3x2－3x3 ≥30 x1 + 2x2－4x3≤80 x1、x2≥0，x3无限制
max z=2x1+2x2－4x3’+4x3” x1 + 3x2－3x3’+3x3” –x4 = 30 x1 + 2x2－4x3+ 4x3” + x5 = 80 x1、x2 、x3’、x3” 、x4、x5 ≥0
称X0为该线性规划对应与基B的一个基本解。
同样，在A中任选m个线性无关的列向量都可以组成一个基， 对应基一个基本解。对于一个LP最多有多少呢？从n个中 选m个进行组合，即：
Cnm=n！/[（n－m）！m！] 因此，基本解是有限的。
举例：找出下列LP所有的基及其对应的基本解 max z=6x1+4x2 2x1 + 3x2≤100 4x1 + 2x2≤120 x1、x2≥0
资源
产品
甲
乙 资源限制
A
1
B
2
C
0
单位产品利润(元/件) 50
1
300kg
1
400kg
1
250kg
100
• 决策变量：x1、x2——分别代表甲、乙两
《线性规划》课件
x1, x2, , xn≥0
其中，bi≥0 (i=1,2,,m)
不符合标准型的几个方面：
⑴目标函数为 min z=c1x1+c2x2++cnxn 令z=-z ,变为 max z= -c1x1- c2x2- -cnxn
⑵约束条件为 a11x1+a12x2++a1nxn≤b1 加入非a1负1x1变+a量12xx2n++1，+称a为1nx松n+弛xn+变1=量b1，有
⑴用一组变量表示某个 线性规划模型的一般形式
方案，一般这些变量取 如下：
值是非负的。
⑵存在一定的约束条件， 可以用线性等式或线性 不等式来表示。
max(min)z c1x1 c2 x2 cn xn a11x1 a12 x2 a1n xn (, )b1 a21x1 a22 x2 a2n xn (, )b2
σ j 3-6M –1+M –1+3M 0 -M 0 0 X4 3 -2 0 1 0 0 -1 10 X6 0 (1) 0 0 -1 1 -2 1 X3 -2 0 1 0 0 0 1 1 σ j 1 -1+M 0 0 -M 0 1-3M X4 (3) 0 0 1 -2 2 -5 12 X2 0 1 0 0 -1 1 -2 1 X3 -2 0 1 0 0 0 1 1
用单纯行法求解线性规划问题后，应回答下面 几个问题：
⑴是否解无界？上面的步骤已作出回答。
⑵是否无可行解？求解后，若人工变量都已取 0，则有可行解；否则，无可行解。
⑶唯一最优解还是无穷多最优解？在最后的单 纯形表中，若所有非基变量的检验数都严格小于0， 则为唯一最优解；若存在某个非基变量的检验数等 于0，则有无穷多最优解。
其中，bi≥0 (i=1,2,,m)
不符合标准型的几个方面：
⑴目标函数为 min z=c1x1+c2x2++cnxn 令z=-z ,变为 max z= -c1x1- c2x2- -cnxn
⑵约束条件为 a11x1+a12x2++a1nxn≤b1 加入非a1负1x1变+a量12xx2n++1，+称a为1nx松n+弛xn+变1=量b1，有
⑴用一组变量表示某个 线性规划模型的一般形式
方案，一般这些变量取 如下：
值是非负的。
⑵存在一定的约束条件， 可以用线性等式或线性 不等式来表示。
max(min)z c1x1 c2 x2 cn xn a11x1 a12 x2 a1n xn (, )b1 a21x1 a22 x2 a2n xn (, )b2
σ j 3-6M –1+M –1+3M 0 -M 0 0 X4 3 -2 0 1 0 0 -1 10 X6 0 (1) 0 0 -1 1 -2 1 X3 -2 0 1 0 0 0 1 1 σ j 1 -1+M 0 0 -M 0 1-3M X4 (3) 0 0 1 -2 2 -5 12 X2 0 1 0 0 -1 1 -2 1 X3 -2 0 1 0 0 0 1 1
用单纯行法求解线性规划问题后，应回答下面 几个问题：
⑴是否解无界？上面的步骤已作出回答。
⑵是否无可行解？求解后，若人工变量都已取 0，则有可行解；否则，无可行解。
⑶唯一最优解还是无穷多最优解？在最后的单 纯形表中，若所有非基变量的检验数都严格小于0， 则为唯一最优解；若存在某个非基变量的检验数等 于0，则有无穷多最优解。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二章 线性规划的对偶理论与灵敏度分析习题
1. 写出下列线性规划问题的对偶问题。
(1)⎪⎪⎩⎪⎪
⎨
⎧≥=++≤++≥++++=无约束
3213213213213
21,0,5343
32243422min x x x x x x x x x x x x x x x z (2) ⎪⎪⎩⎪⎪
⎨
⎧≤≥≤++≥-+-=++++=0
,0,8374355
22365max 3213213213213
21x x x x x x x x x x x x x x x z 无约束
(3)⎪⎪
⎪⎪⎩
⎪⎪⎪
⎪⎨⎧==≥=====∑∑∑∑====)
,,1;,,1(0)
,,1(),,1(min 1
111n j m i x n j b x m i a x x c z ij m
i j ij n
j i ij m
i ij
n
j ij (4)⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=≥++==<=<=∑∑∑===),,,,1(0),,2,1()
,,1(min 1
211111n n j x m m m i b x a m m i b x a x c z j n j i j ij n
j i j ij n
j j
j 无约束 2. 判断下列说法是否正确，为什么?
(1)如果线性规划的原问题存在可行解，则其对偶问题也一定存在可行解； (2)如果线性规划的对偶问题无可行解，则原问题也一定无可行解； ( 3)在互为对偶的一对原问题与对偶问题中，不管原问题是求极大或极小，原问题可行解的目标函数值一定不超过其对偶问题可行解的目标函数值；
(4)任何线性规划问题具有唯一的对偶问题。
3. 已知某求极大化线性规划问题用单纯形法求解时的初始单纯形表及最终单纯形表如下表所示，求表中各括弧内未知数的值。
⎪⎩⎪
⎨⎧=≥-≤+-+-≥++++++=)4,,1(0322326532min 432143214
321 j x x x x x x x x x x x x x z j
(1)写出其对偶问题；(2)用图解法求解对偶问题；(3)利用(2)的结果及根据对偶问题性质写出原问题最优解。
5. 给出线性规划问题
⎪⎪⎩⎪⎪
⎨
⎧≤≥≥++=+-≤-+++=无约束
321321321321321,0,0221222max x x x x x x x x x x x x x x x z (1)写出其对偶问题；(2)利用对偶问题性质证明原问题目标函数值z ≤1。
6. 已知线性规划问题
⎪⎩⎪⎨⎧≥≤-+-≤++-+=0,,122
max 3
213213212
1x x x x x x x x x x x z
试根据对偶问题性质证明上述线性规划问题目标函数值无界。
7. 给出线性规划问题
⎪⎪⎪⎩⎪
⎪⎪
⎨⎧=≥≤++≤++≤+≤+++++=)
4,,1(09
6628342max 3
21432214214321 j x x x x x x x x x x x x x x x x z j
要求：（1）写出其对偶问题；（2）已知原问题最优解为X *
=(2,2,4,0)，试根据对
偶理论，直接求出对偶问题的最优解。
8. 已知线性规划问题A 和B 如下：
问题A 问题B
()
⎪
⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=≥≤≤≤=∑∑∑∑====n j x y b x a y b x a y b x a x c z j n
j j j n
j j j n
j j j n
j j
j ,,10max 3133212
21
1111 对偶变量
()
⎪
⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=≥+≤+≤≤=∑∑∑∑====n j x y b b x a a y b x a y b x a x c z j n
j j j j n j j j n
j j j n
j j
j ,,10ˆ3)3(ˆ51
51ˆ55max 311313212
211
1
11
对偶变量
试分别写出i y
ˆ同)3,2,1(=i y i 间的关系式。
9. 用对偶单纯形法求解下列线性规划问题。
（1）⎪⎩⎪
⎨⎧=≥≥+≥+++=)3,2,1(05
223318124min 32213
21j x x x x x x x x z j
（2）⎪⎩⎪
⎨⎧=≥≥++≥++++=)3,2,1(010*********min 3214213
21j x x x x x x x x x x z j
10. 考虑如下线性规划问题：
⎪⎪⎩
⎪⎪⎨
⎧=≥≥++≥++≥++++=)3,2,1(03222434223804060min 321321321321j x x x x x x x x x x x x x z j
要求：(1)写出其对偶问题；(2)用对偶单纯形法求解原问题；(3)用单纯形法求解其对偶问题；(4)对比(2)与(3)中每步计算得到的结果。
11. 已知线性规划问题：
⎪⎩⎪
⎨⎧=≥≤+-≤+++-=)3,2,1(0426
2max 2
2321321j x x x x x x x x x z j
先用单纯形法求出最优解，再分析在下列条件单独变化的情况下最优解的变化。
(1)目标函数变为max z ＝2x 1+3x 2+x 3；
(2)约束右端项由⎪⎪⎭⎫ ⎝⎛46变为⎪⎪⎭
⎫
⎝⎛43。
(3)增添一个新的约束条件-x 1+2x 3≥2。
12. 给出线性规划问题
⎪⎪⎪
⎩
⎪⎪
⎪⎨⎧=≥≤++≤++++=)3,2,1(03373431
131313132max 221321321j x x x x x x x x x x z j 用单纯形法求解得最终单纯形表见下表。
(1)目标函数中变量x 3的系数变为6；
(2)分别确定目标函数中变量x l 和x 2的系数c 1、c 2在什么范围内变动时最优解不 变；
（3）约束条件右端项由⎪⎪⎭⎫
⎝⎛31变为⎪⎪⎭
⎫ ⎝⎛32；
（4）增加一个新的变量7,11,666=⎪⎪⎭
⎫
⎝⎛=c P x ；
(5)增添一个新的约束x 1+2x 2+x 3≤4。
13. 分析下列线性规划问题中，当且变化时最优解的变化，并画出z (λ)对λ的变化关系图。
()
()
()()()()()
⎪⎪⎩
⎪
⎪⎨⎧
⎪⎪⎩⎪⎪⎨
⎧=≥≤-≤+≤+=≥=++=++++--=+-+=2,10112610524,105322223max 22min 1212121421431214321j x x x x x x x j x x x x x x x x x z x x x x z j j λλλλλ
()
()()
()()()
⎪⎪⎩
⎪
⎪⎨⎧
⎪⎪⎩⎪⎪⎨
⎧=≥-≤++≤+-≤++=≥+-=+--=--++=+++=3,2,107304260234024,10122523max 42min 321313214324313214321j x x x x x x x x j x x x x x x x x x x z x x x x z j j λλλλλλλ
14. 某厂生产A ，B ，C 三种产品，其所需劳动力、材料等有关数据见下表。
要
求：(1)确定获利最大的产品生产计划；(2)产品A 的利润在什么范围内变动时，上述最优计划不变；(3)如果设计一种新产品D ，单件劳动力消耗为8单位，材料消耗为2单位，每件可获利3元，问该种产品是否值得生产?(4)如果劳动力数量不增，材料不足时可从市场购买，每单位0.4元。
问该厂要不要购进原材料扩大生产，以购多少为宜。
15.已知线性规划问题
⎪⎩⎪
⎨⎧=≥+=++++=++++++++=)5,...,1(0300)(max 225323222121214313212111543322111j x t b x x a x a x a t b x x a x a x a x x x c x c x t c z j
当021==t t 时求得解最终单纯形表进见下表。
（1）确定232221*********,,,,,,,,a a a a a a c c c 和21,b b 的值； （2） 当02=t 时，1t 在什么范围内变化上述最优解不变； （3）当01=t 时，2t 在什么范围内变化上述最优基不变；
16．某文教用品厂利用原材料白坯纸生产原稿纸、日记本和练习本三种产品。
该厂有工人100人，每天白坯纸的供应量为30000kg 。
如单独生产各种产品时，每个工人每天可生产原稿纸30捆，或日记纸30打，或练习本30箱。
已知原材料消耗为：每捆原稿纸用白坯纸313
kg, 每打日记本用白坯纸3
1
13kg, 每箱练习本用白坯纸 3
2
26kg 。
已知生产各种产品的赢利为：每捆原稿纸1元，每打日记本2元，每箱练习本3元。
试决定：（1）在现有生产条件下使该厂赢利最大的方案；（2）如白坯纸供应量不变，而工人数量不足时可从市场上招收临时工，临时工费用为每人每天15元。
问该厂应否招临时工及招收多少人为宜。