基于MATLAB的线性分组码课程设计论文
- 格式:doc
- 大小:290.32 KB
- 文档页数:13

信息论与编码实验报告1、认真阅读课本中关于线性分组码的基本原理及特点等内容,并简要写出其基本原理及特点;解:基本原理:对信源编码器输出的D 进制序列进行分组,设分组长度为k ,相应的码字表示为),,,(12m m m k M ∙∙∙=→,其中每个码元()k i m i≤≤1都是D 进制的显然这样的码字共有kD 个。
特点:一个()k n ,线性分组码中非零码字的最小重量等于该码的最小距离min d 。
2、写出(7,4)线性分组码编解码基本步骤,画出程序流程图;编码流程图 译码流程图 (7,4)汉明码的编码就是将输入的4 位信息码M=[ 3456a a a a ]加上3 位监督码012b b b 从而编成7位汉明码[6a 012345,,,,,a a a a a a ],编码输出B=[6a 5a 4a 3a 2a 1a 0a ].由式A = M ·G=[3456a a a a ]·G 可知,信息码M 与生成矩阵G 的乘积就 是编好以后的(7,4)汉明码3、实现(7,4)线性分组码编解码的Matlab源程序;构造BSC传输信道中采用(7,4)线性分组码的Simulink仿真程序。
(7,4)汉明码的编码程序:library ieee;use ieee.std_logic_1164.all;entity bm isport(a:in std_logic_vector(3 downto 0);but std_logic_vector(6 downto 0));end ;architecture one of bm isbeginb(6)<=a(3);b(5)<=a(2);b(4)<=a(1);b(3)<=a(0);b(2)<=a(3) xor a(2) xor a(1);b(1)<=a(3) xor a(2) xor a(0);b(0)<=a(3) xor a(1) xor a(0);end;(7,4)汉明码的译码程序:library ieee;use ieee.std_logic_1164.all;entity ym isport(a:in std_logic_vector(6 downto 0);sut std_logic_vector(2 downto 0);but std_logic_vector(3 downto 0);cut std_logic_vector(2 downto 0));end ;architecture one of ym isbeginprocess(a)variable ss:std_logic_vector(2 downto 0);variable bb:std_logic_vector(6 downto 0);beginss(2):=a(6) xor a(5) xor a(4) xor a(2);ss(1):=a(6) xor a(5) xor a(3) xor a(1);ss(0):=a(6) xor a(4) xor a(3) xor a(0);bb:=a;if ss> "000" thencase ss iswhen "001" =>bb(0):= not bb(0);c<="000";when "010" =>bb(1):= not bb(1);c<="001";when "100" =>bb(2):=not bb(2);c<="010";when "011" =>bb(3):=not bb(3);c<="011";when "101" =>bb(4):=not bb(4);c<="100";when "110" =>bb(5):=not bb(5);c<="101";when "111" =>bb(6):=not bb(6);c<="110";when others => null;c<="111";end case;else b<= a(6)&a(5)&a(4)&a(3);end if;s<=ss;b<=bb(6)&bb(5)&bb(4)&bb(3);end process;end;4、讨论(7,4)线性分组码的最小码距与码重及纠错能力的关系,讨论采用纠错编码和不采用纠错编码对传输系统的影响。

第24卷第1期 2005年1月实验室研究与探索RESEARCH AND EXPLORATION IN LABORATORYVol.24No.1 Jan.2005基于MATLAB 的信道编码教学实验软件设计与实现张海涛, 王福昌(华中科技大学 电工电子教学基地湖北武汉430074)摘 要:介绍了基于MATLAB 的信道编码教学实验软件,主要包括实验操作界面制作以及循环码和卷积码编译码。
关键词: 矩阵实验室 软件包;循环码;卷积码;编译码;界面中图分类号:TN911.22文献标识码:B文章编号:1006 7167(2005)01 0046 04Design and Realization of the Teaching ExperimentalSoftware on Channel Coding with MATLABZ HANG Hai tao , WANG Fu chang(Instruction Base of Electrotechnics&Electtronics,Huazhong Univ.of Science and Technology,W uhan 430074,China)Abstract :This paper introduceds a teaching experimentel software based on channel coding with MATLAB,including the design of experiment interface ,the encode decode process of cyclic code and convolutional code.Key words :MATLAB (Matrix Laboratory);cyclic code;convolutional code;encode decode;interface收稿日期:2004 04 09作者简介:张海涛(1978-),男,汉族,湖北红安人,硕士研究生三年级,主要从事通信与信号处理方面的科研。


青岛农业大学信息与编码理论实验报告姓名:韩祖良班级:信计1201学号:20125991指导老师:辛永训2015年6月信息与编码理论实验课:实验一实验题目Shannon码的编码实验目的掌握MATLAB基本操作;Shannon码的编码实验地点及时间信息楼214机房,周一上午1-2节;周三上午3-4节实验内容1. MATLAB简介及常用功能;2.离散信源的MATLAB分析;3.离散信道的MATLAB分析;4.Shannon码的编码原理及软件实现。
实验习题1.你对MATLAB软件的了解;答:我参加过数学建模国赛和美赛,获得过省级二等奖和美赛成功参与奖,更期待今年10月份的国赛可以有所突破。
我对MATLAB比较熟悉,在建模过程中经常用的是其强大的计算和编程绘图功能。
其操作简单,不像c语言等需要抽象的编程语言,使用的大多直接是数学中的符号,而且快捷键很方便,比如输入“clc”命令就可以清屏、输入“plot(x,y)命令”就可以绘制二维图像。
编程制图方面,可以直接打开代码本,不用将代码敲入主界面,建模过程中印象比较深刻的是去年国赛A题嫦娥二号着陆点的月球剖面图就可以用MATLAB绘制,其在代码中是一个1000*1000的矩阵,而矩阵数字的突变代表了月球剖面图的高低。
同样,B题设计折叠椅的动图模型也是用MATLAB做出来的。
下面较为详细的介绍一下MATLAB,MATLAB是美国MathWorks公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括MATLAB和Simulink两大部分。
它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中,代表了当今国际科学计算软件的先进水平。
MATLAB和Mathematica、Maple并称为三大数学软件。
它在数学类科技应用软件中在数值计算方面首屈一指。
MATLAB可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连matlab开发工作界面接其他编程语言的程序等,主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。

1 绪论随着经济全球化的不断发展,企业面临更加激烈的市场竞争。
企业必须不断提高盈利水平,增强其获利能力,在生产、销售、新产品研发等一系列过程中只有自己的优势,提高企业效率,降低成本,形成企业的核心竞争力,才能在激烈的竞争中立于不败之地。
过去很多企业在生产、运输、市场营销等方面没有利用线性规划进行合理的配置,从而增加了企业的生产,使企业的利润不能达到最大化。
在竞争日益激烈的今天,如果还按照过去的方式,是难以生存的,所以就有必要利用线性规划的知识对战略计划、生产、销售各个环节进行优化从而降低生产成本,提高企业的效率。
在各类经济活动中,经常遇到这样的问题:在生产条件不变的情况下,如何通过统筹安排,改进生产组织或计划,合理安排人力、物力资源,组织生产过程,使总的经济效益最好。
这样的问题常常可以化成或近似地化成所谓的“线性规划”(Linear Programming,简记为LP)问题。
线性规划是应用分析、量化的方法,对经济管理系统中的人、财、物等有限资源进行统筹安排,为决策者提供有依据的最优方案,以实现有效管理。
利用线性规划我们可以解决很多问题。
如:在不违反一定资源限制下,组织安排生产,获得最好的经济效益(产量最多、利润最大、效用最高)。
也可以在满足一定需求条件下,进行合理配置,使成本最小。
同时还可以在任务或目标确定后,统筹兼顾,合理安排,用最少的资源(如资金、设备、原材料、人工、时间等)去完成任务。
2 线性规划模型的建立与求解2.1线性规划模型线性规划的目标函数可以是求最大值,也可以是求最小值,约束条件可以是不等式也可以是等式,变量可以有非负要求也可以没有非负要求(称这样的变量为自由变量)。
为了避免这种由于形式多样性而带来的不便,规定线性规划的标准形式为112211112211211222221122,min ...,,···0(1,2,,).n n n n n n m m mn n m i z f x f x f x s t a x a x a x b a x a x a x b a x a x a x b x i n =+++⎧⎪+++≤⎪⎪+++≤⎪⎨⎪⎪+++≤⎪≥=⎪⎩极小值模型112211112211211222221122max ...,,,0(1,2,,).n n n n n n m m mn n m i z f x f x f x s t a x a x a x b a x a x a x b a x a x a x b x i n =+++⎧⎪+++≥⎪⎪+++≥⎪⎨⎪⎪+++≥⎪≥=⎪⎩极大值模型 利用矩阵与向量记为min ..0T z C xs t Ax b x ⎧=⎪=⎨⎪≥⎩其中C 和x 为n 维列向量,b 为m 维列向量,b ≥0,A 为m ×n 矩阵,m<n 且rank(A)=m 。

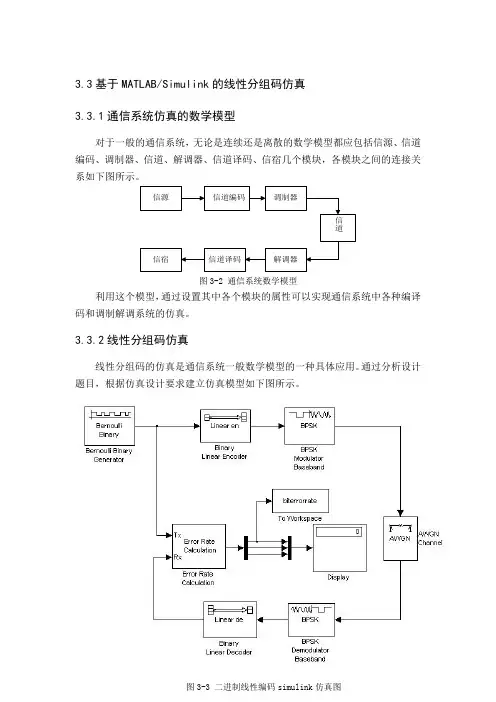
3.3基于MATLAB/Simulink的线性分组码仿真3.3.1通信系统仿真的数学模型对于一般的通信系统,无论是连续还是离散的数学模型都应包括信源、信道编码、调制器、信道、解调器、信道译码、信宿几个模块,各模块之间的连接关系如下图所示。
信源信道编码调制器信宿信道译码解调器信道图3-2 通信系统数学模型利用这个模型,通过设置其中各个模块的属性可以实现通信系统中各种编译码和调制解调系统的仿真。
3.3.2线性分组码仿真线性分组码的仿真是通信系统一般数学模型的一种具体应用。
通过分析设计题目,根据仿真设计要求建立仿真模型如下图所示。
图3-3 二进制线性编码simulink仿真图上图为二进制线性编码的simulink仿真图信源、信道编译码器和误码率计算器等模块的参数设置情况见表3-1至表3-6。
调制器选用调制性能较好的BPSK调制器;与调制和编码相对应的,解调器选用BPSK解调器,译码器选用二进制线性译码器。
本设计希望借助线性分组码的误码率曲线来研究其性能,所以需要加入误码率计算器(Error Rate Calculation)。
通过学习MATLAB/simulink相关知识,了解到误码率计算器输出三个结果:误码率、正确码元个数和错误码元个数。
设计所关心的是误码率,所以先用分路器将三路信号分离,然后将误码率的值输出到工作空间(workspace)便于提取每一秒的仿真数据,为了实现和显示模块(display)的连接,必须用合路器将分开的信号重新组合起来。
而选用Display作为显示模块,是因为它可以方便快捷的观察到三路输出信号的动态变化过程。
其中主要模块的参数设置如下表所示。
表3-1是信源模块的参数设置表,由于在实际通信过程中,具体环境不同信源信号的形式可能多种多样,为了模拟最一般的信号形式,图中信源选择能产生伯努利分布的二进制随机数的Bernoulli Random Binary Generator模块;编码器选用二进制线性编码器;表3-1 伯努利二进制随机数生成器(Bernoulli Random Binary Generator)参数表参数名称参数值Probability of zer(0出现的概率)0.5Initial seed(初始化种子)21375Sample time(抽样时间)0.0001Frame-based outputs(输出基于帧)√Samples per frame(每帧抽样数)(根据要仿真信号的信息位数设定数值如(7,4)码则此项值为4)研究二进制线性码的性能当然用二进制线性编码器。

河海大学物联网工程学院(常州)MATLAB课程设计报告学年学期2014-2015 第一学期项目名称万能时钟成员指导教师目录一.分组分工 (3)二.设计理念 (3)三.模块设计 (4)四.缺憾补充 (11)五.实践心得 (11)一.分组分工二.设计理念时钟与我们的生活息息相关。
远渡他国,我们需要调节时差,以确认正确的当地时间;睡梦中,我们需要闹钟将我们唤醒;800米起跑线上,我们需要计时器记录我们的用时成绩······一个集多种功能的时钟可以大大方便我们的生活。
经过商议,我们确定MATLAB设计的课题为设计一个多功能时钟。
它包含时钟功能、计时功能、闹钟功能。
其中时钟功能默认显示北京时间,也可以随时随意更换其他时区的时刻;闹钟功能支持音频以及视频的播放,除了系统自带的音乐,我们也可以根据自身爱好,选择其他音乐。
三.模块设计(1)模块名称:时钟模块模块功能:界面出现实时时钟和可转换时区模块背景描述:白色背景有一个时钟设计思路及技术要点:将系统实时时间转换成时钟的秒针分针时针的位置,时区时间变成一个可选择的关键代码及描述:计算时针.分针.秒针的位置function TimeUpdate(obj,eventdata,handles) %定时器回调函数global VarTime;global Title;%VarTimeNowTime=fix(clock);if NowTime(4)+VarTime<0NowTime(3)=NowTime(3)-1;NowTime(4)=NowTime(4)+VarTime+24;elseif NowTime(4)+VarTime>=24NowTime(3)=NowTime(3)+1;NowTime(4)=NowTime(4)+VarTime-24;elseNowTime(4)=NowTime(4)+VarTime;endStrTime= sprintf('%d年%d月%d日%d时%d分%d秒',NowTime);set(handles.date,'String',StrTime);%global hh;global hm;global hs;axes(handles.axes1);ti=NowTime;%ti=clock;% 计算时针位置th=-(ti(4)+ti(5)/60+ti(6)/3600)/12*2*pi+pi/2;xh3=4.0*cos(th);yh3=4.0*sin(th);xh2=xh3/2+0.5*cos(th-pi/2);yh2=yh3/2+0.5*sin(th-pi/2);xh4=xh3/2-0.5*cos(th-pi/2);yh4=yh3/2-0.5*sin(th-pi/2);set(hh,'XData',[0 xh2 xh3 xh4 0],'YData',[0 yh2 yh3 yh4 0])% 计算分针位置tm=-(ti(5)+ti(6)/60)/60*2*pi+pi/2;xm3=6.0*cos(tm);ym3=6.0*sin(tm);xm2=xm3/2+0.5*cos(tm-pi/2);ym2=ym3/2+0.5*sin(tm-pi/2);xm4=xm3/2-0.5*cos(tm-pi/2);ym4=ym3/2-0.5*sin(tm-pi/2);set(hm,'XData',[0 xm2 xm3 xm4 0],'YData',[0 ym2 ym3 ym4 0])% 计算秒针位置ts=-(ti(6))/60*2*pi+pi/2;set(hs,'XData',[0 7*cos(ts)],'YData',[0 7*sin(ts)])drawnow;分区选择switch TimeZoneString{SelZone} %以北京时间为例,VarTime=0; 以后要加其它的时区,只要按如下格式输入case分支,并且在popupmenu 为TimeZone中输入相应的字符串,例如北京时间为(GMT+08:00)北京时间case '(GMT-12:00)日界线西'Title='日界线西时间';set(handles.TimeZoneStr,'string',Title);VarTime=-20;case '(GMT-10:00)夏威夷时间'Title='夏威夷时间';set(handles.TimeZoneStr,'string',Title);VarTime=-18;case '(GMT-06:00)中部时间(美国)'Title='中部时间(美国)';set(handles.TimeZoneStr,'string',Title);VarTime=-14;case '(GMT-04:00)加拿大时间'Title='加拿大时间';set(handles.TimeZoneStr,'string',Title);VarTime=-12;case '(GMT)格林威治标准时间'Title='格林威治标准时间'set(handles.TimeZoneStr,'string',Title);VarTime=-8;case '(GMT+02:00)雅典时间'Title='雅典时间';set(handles.TimeZoneStr,'string',Title);VarTime=-6;case '(GMT+03:00)莫斯科时间'Title='莫斯科时间';set(handles.TimeZoneStr,'string',Title);VarTime=-5;case '(GMT+08:00)北京时间'Title='北京时间';set(handles.TimeZoneStr,'string',Title);VarTime=0;case '(GMT+09:00)东京时间'Title='东京时间';set(handles.TimeZoneStr,'string',Title);VarTime=1;case '(GMT+10:00)堪培拉时间'Title='堪培拉时间';set(handles.TimeZoneStr,'string',Title);VarTime=2;End(2)模块名称:计时模块模块功能:界面出现计时器模块背景描述:无设计思路及技术要点:不停的刷新与开始的时间差来达到计时功能,全部使用UI控件关键代码及描述:计时器中的选择功能有开始暂停恢复从置退出等选项switch cmdcase 'START'if LAPFLAGt = toc;tic;TIME = TIME + t;elsetic;endSTOPPED = 0;set(START, 'String', '暂停', 'Callback', [mfilename, '(''PAUSE'')']);% set(LAP, 'Enable', 'on');while ~STOPPEDt = toc; str = format_time(TIME + t); set(DISPLAY, 'String', str); pause(0.01); %中断0.01秒endcase 'LAP'STOPPED = 1; LAPFLAG = 1; t = toc;str = format_time(TIME + t); set(DISPLAY, 'String', str);set(START, 'String', '恢复', 'Callback', [mfilename, '(''START'')']); case 'PAUSE'STOPPED = 1; LAPFLAG = 0; t = toc; TIME = TIME + t;str = format_time(TIME); set(DISPLAY, 'String', str);set(START, 'String', '恢复', 'Callback', [mfilename, '(''START'')']); set(LAP, 'Enable', 'off');case 'RESET'STOPPED = 1; LAPFLAG = 0; TIME = 0;str = format_time(TIME); set(DISPLAY, 'String', str);set(START, 'String', '开始', 'Callback', [mfilename, '(''START'')']); set(LAP, 'Enable', 'off');case 'EXIT'STOPPED = 1;close(HFIG);case 'KEY'switch upper(get(HFIG, 'CurrentCharacter'))case 'L'if strcmp(get(LAP, 'Enable'), 'on')feval(mfilename, 'LAP');endcase 'R'feval(mfilename, 'RESET');case 'X'feval(mfilename, 'EXIT');otherwiseeval(get(START, 'Callback'));endotherwisereturnEnd(3)模块名称:闹钟模块模块功能:界面音乐闹钟模块背景描述:无设计思路及技术要点:获取当前时间,与自己下拉菜单选择的时间相比较。

重庆交通大学信息科学与工程学院综合性设计性实验报告专业:通信工程专业12级学号:631206040105姓名:刘志坤实验所属课程:信息论与编码实验室(中心):软件与通信实验中心指导教师:黄大荣2015年4月线性分组码的matlab实现一、实验目的和要求。
信道编码的目的是为了改善通信系统的传输质量。
按照监督码元与信息码元之间的关系,有线性码和非线性码。
线性码的特点是监督码元与信息码元之间有线性关系,可用一组线性代数方程将其联系起来。
本实验用Matlab语言编程实现线性分组码。
二、实验原理。
线性分组码的编码包括两个基本步骤:首先将信源的输出序列分为k位一组的消息组(也称信息组,简称消息或信息);然后信道编码器按照一定的编码规则将k位消息变换为n个码元的码字。
一个(n,k)线性分组码,如果码的数域为GF(m),即每一个码元可能有m种取值,则信源可发出km种不同的消息。
对于(n,k)码,n表示码长,k表示信息码元的维数,也就是子空间的维数,设M=[m1,m2,…,mk]是输入纠错码编码器的信息,则由纠错码编码器输出的码字C=MGG为该(n,k)码的生成矩阵。
如果只考虑信道编码,则纠错码通信系统模型可归结为如下模型:线性分组码(n ,k )中许用码字(组)为2k 个。
定义线性分组码的加法为模二加法,乘法为二进制乘法。
即1+1=0、1+0=1、0+1=1、0+0=0;1×1=1、1×0=0、0×0=0、0×1=0。
且码字与码字的运算在各个相应比特位上符合上述二进制加法运算规则。
线性分组码具有如下性质(n ,k )的性质:1、封闭性。
任意两个码组的和还是许用的码组。
2、码的最小距离等于非零码的最小码重。
对于码组长度为n 、信息码元为k 位、监督码元为r =n -k 位的分组码,常记作(n ,k )码,如果满足2r -1≥n ,则有可能构造出纠正一位或一位以上错误的线性码。

信息工程学院通信工程系设计题目:基于MATLAB的线性分组码编译码仿真设计班级:10通信班学号:姓名:指导老师:2013 年11 月15 日成绩:摘要该系统是(6,3)线性分组码的编码和译码的实现,它可以对输入的三位的信息码进行线性分组码编码,对于接收到的六位码字可以进行译码,从而译出三位信息码。
当接收到的六位码字中有一位发生错误时,可以纠正这一位错码;当接收到的码字有两位发生错误时,只能纠正一位错误,但同时能检测出另一位错误不能纠正。
只有特定位有两位错误时,才能纠正两位错误。
这样就译出正确的信息码组,整个过程是用MATLAB语言实现的。
关键词:编码; 译码; 纠错目录前言 (2)第1章设计目标 (2)第2章 MATLAB简介 (3)第3章基本原理 (3)3.1 线性分组码的编码 (3)3.1.1 生成矩阵 (3)3.1.2 校验矩阵 (5)3.2 伴随式与译码 (6)3.2.1 码的距离及纠检错能力 (6)3.2.2 伴随式与译码 (6)第4章推导过程 (7)4.1 编码过程 (7)4.2 译码过程 (9)第5章仿真程序及结果分析 (11)5.1 仿真程序 (11)5.2 仿真结果图 (13)5.3 结果分析 (15)参考文献 (16)总结 (17)0 1 11 0 1 1 1 0 前言近年来,随着计算机、卫星通信及高速数据网的飞速发展,数据的交换、处理和存储技术得到了广泛的应用,人们对数据传输和存储系统的可靠性提出了越来越高的要求。
因此,如何控制差错、提高数据传输和存储的可靠性,成为现代数字通信系统设计的重要课题。
目前,绝大多数的数字计算机和数字通信系统中广泛采用二进制形式的码。
而线性分组码具有编译码简单,封闭性好等特点,采用差错控制编码技术是提高数字通信可靠性的有效方法,是目前较为流行的差错控制编码技术。
对线性分组码的讨论都在有限域GF(2)上进行,域中元素为{0,1},域中元素计算为模二加法和模二乘法。

基于MATLAB的线性代数实用教程课程设计一、引言线性代数是数学中的重要分支,常用于解决科学和工程领域中的线性问题。
MATLAB作为一款广泛应用于科学计算和工程领域的软件工具,提供了丰富的线性代数工具和应用。
因此,本文将基于MATLAB,设计一份线性代数实用教程,旨在帮助初学者了解和掌握线性代数的基本概念、方法和应用,并在MATLAB环境中进行实践。
二、教程内容1. 线性代数基础线性代数基础部分主要介绍线性代数的基本概念和理论知识,包括向量、矩阵、矩阵的运算、方程组的解法等内容。
具体包括以下几个方面:1.坐标系和向量的概念2.向量的线性运算和内积3.矩阵的定义和运算4.矩阵的转置、逆、行列式5.齐次和非齐次线性方程组及其解法2. MATLAB线性代数工具MATLAB作为一款优秀的数学软件,为线性代数的计算和应用提供了非常丰富的工具和函数。
在本部分中,我们将介绍MATLAB中的一些常用的线性代数工具和函数,包括:1.矩阵的创建和输入输出2.矩阵的运算和变换3.线性方程组的解法4.特征值和特征向量的计算5.矩阵分解和奇异值分解3. MATLAB线性代数应用案例在实际应用中,线性代数常常被用于解决科学和工程领域中的各种问题。
在本部分中,我们将介绍一些MATLAB中的线性代数应用案例,包括:1.图像处理中的线性代数应用2.信号处理中的线性滤波和变换3.控制工程中的控制系统分析和设计三、教程设计与实现本教程将采用以下教学设计方法:1.通过文字和图表的形式,介绍线性代数的基本概念,原理和计算方法。
2.通过MATLAB环境中的实例演示,使学生能够直观地理解线性代数的应用和操作方法。
3.通过编写作业和练习题,使学生能够独立完成线性代数的基本计算和应用。
具体实现方式如下:1.使用Markdown格式编写线性代数的相关知识和内容。
2.使用MATLAB编写相应的代码,并以图表和文本的形式展示。
3.每节课结束后,编写相应的练习题,供学生巩固所学知识。
信息工程学院通信工程系设计题目:基于MATLAB的线性分组码编译码仿真设计班级:10通信班学号:姓名:指导老师:2013 年11 月15 日成绩:摘要该系统是(6,3)线性分组码的编码和译码的实现,它可以对输入的三位的信息码进行线性分组码编码,对于接收到的六位码字可以进行译码,从而译出三位信息码。
当接收到的六位码字中有一位发生错误时,可以纠正这一位错码;当接收到的码字有两位发生错误时,只能纠正一位错误,但同时能检测出另一位错误不能纠正。
只有特定位有两位错误时,才能纠正两位错误。
这样就译出正确的信息码组,整个过程是用MATLAB语言实现的。
关键词:编码; 译码; 纠错目录前言 (2)第1章设计目标 (2)第2章 MATLAB简介 (3)第3章基本原理 (3)3.1 线性分组码的编码 (3)3.1.1 生成矩阵 (3)3.1.2 校验矩阵 (5)3.2 伴随式与译码 (6)3.2.1 码的距离及纠检错能力 (6)3.2.2 伴随式与译码 (6)第4章推导过程 (7)4.1 编码过程 (7)4.2 译码过程 (9)第5章仿真程序及结果分析 (11)5.1 仿真程序 (11)5.2 仿真结果图 (13)5.3 结果分析 (14)参考文献 (16)总结 (17)前言近年来,随着计算机、卫星通信及高速数据网的飞速发展,数据的交换、处理和存储技术得到了广泛的应用,人们对数据传输和存储系统的可靠性提出了越来越高的要求。
因此,如何控制差错、提高数据传输和存储的可靠性,成为现代数字通信系统设计的重要课题。
目前,绝大多数的数字计算机和数字通信系统中广泛采用二进制形式的码。
而线性分组码具有编译码简单,封闭性好等特点,采用差错控制编码技术是提高数字通信可靠性的有效方法,是目前较为流行的差错控制编码技术。
对线性分组码的讨论都在有限域GF(2)上进行,域中元素为{0,1},域中元素计算为模二加法和模二乘法。
分组码是一组固定长度的码组,可表示为(n , k),通常它用于前向纠错。
线性码(Linear Code)是按照一组线性方程构成的,它的信息位和监督位是由一些线性代数方程联系的。
线性码具有便于运算分析的叠加性质,具有较强的纠错能力等特点。
本文主要是利用MATLAB环境下的Simulink通信系统仿真模型库平台进行线性码建模仿真,仿真模型主要包括伯努利随机二进制信号发生器模块、二进制线性码编码器模块、二进制线性码均衡信道模块、二进制线性码译码器模块、误码率显示与计算分析模块。
其中,信号发生器模块用于产生二进制随机信号并将它输出,编码器模块用于将产生的二进制信号进行编码,均衡信道模块用于对二进制信号的误码率性能进行仿真、并将二进制噪声添加到输入信号,译码器模块用于将产生的二进制信号进行译码,误码率模块用于计算和显示此配置参数情况下的误码率。
仿真结果表明,线性码误码率低、冗余度小、纠错能力强,适用于二次剩余码、数字签名、认证码、密钥管理等方面。
关键词:线性码;MATLAB;Simulink;编译码;误码率1 课程设计目的 (1)2 课程设计要求 (1)3 相关知识 (1)4 课程设计分析 (2)4.1课题相关概念 (2)4.2 线性码结构流程图设计 (2)5 仿真 (3)5.1线性码仿真模型图 (3)5.2各模块参数设置 (4)5.3仿真结果 (7)6 结果分析 (7)7 参考文献 (9)线性码仿真1 课程设计目的(1)巩固并扩展通信原理课程的基本概念,基本理论,分析方法和实现方法。
(2)学习和掌握MATLAB和SIMULINK软件的使用,并用它们进行建模,了解其设计方法。
(3)培养创新思维和设计能力。
(4)增强软件编程实现能力和解决能力。
2 课程设计要求(1)掌握线性码的编码与译码的相关知识。
(2)能够设计程序并建立模型。
(3)通过程序调出并运行模型,并产生误码率与频谱的关系曲线图。
3 相关知识MATLAB[1] 是美国MathWorks公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括MATLAB和Simulink两大部分。
实验二线性分组码的编译码报告1.实验目的线性分组码是一种常用的编码方式,本实验旨在通过对线性分组码的编码与解码操作,加深对线性分组码的理解,并掌握编码与解码的基本方法。
2.实验原理2.1线性分组码线性分组码是一种纠错码,通过在数据中嵌入冗余信息,使得数据在传输或存储过程中能够进行纠错。
线性分组码中的每个码字都由一系列的信息位和校验位组成,校验位的数量和位置由特定的生成矩阵决定。
2.2编码编码是将信息位转换为码字的过程。
对于线性分组码,编码过程可以通过生成矩阵来实现。
生成矩阵是一个以二进制元素组成的矩阵,其列数等于码字的长度,行数等于信息位的长度。
生成矩阵的乘法运算可以将信息位转换为码字。
2.3解码解码是将接收到的码字转换为信息位的过程。
对于线性分组码,解码过程可以通过校验矩阵来实现。
校验矩阵是生成矩阵的转置矩阵,其列数等于校验位的数量,行数等于码字的长度。
解码过程可以通过校验矩阵的乘法运算来恢复信息位。
3.实验内容3.1编码操作首先,选择一个合适的生成矩阵,根据生成矩阵进行编码操作。
具体步骤如下:1)定义生成矩阵,并将其转换为标准型;2)输入信息位;3)将信息位与生成矩阵相乘,得到码字;4)输出码字。
3.2解码操作在编码操作完成后,进行解码操作,根据生成矩阵得到校验矩阵,并根据校验矩阵进行解码操作。
具体步骤如下:1)根据生成矩阵得到校验矩阵;2)输入码字;3)将码字与校验矩阵相乘,得到校验位;4)判断校验位是否全为0,若是则解码成功,将码字中的信息位输出;若不是,则说明有错误发生,进行纠错操作。
4.实验结果与分析通过编码与解码的操作,得到了编码后的码字,并成功地将码字解码为原始信息位。
在解码过程中,如果校验位全为0,则说明接收到的码字没有发生错误,并且成功恢复出了信息位。
5.实验总结通过本次实验,深入理解了线性分组码的编码与解码原理,并掌握了编码与解码的基本方法。
线性分组码是一种常用的纠错码,其应用广泛,并且在通信与存储领域发挥着重要作用。
课程设计(论文)任务书数学与计算科学学院学院数学与应用数学专业信计08-01 班课程名称数学软件课程设计题目 MATLAB中三维曲面及其色彩处理问题的研究任务起止日期: 2009 年 12 月 14 日~ 2009年 12月 25 日学生姓名胡任庭学号 200853100125指导教师仝青山教研室主任年月日审查课程设计(论文)任务注:1. 此任务书由指导教师填写。
如不够填写,可另加页。
2. 此任务书最迟必须在课程设计(论文)开始前下达给学生。
学生送交全部材料日期学生(签名)指导教师验收(签名)第1章构建三维MATLAB图形1.1 构建三维曲面的基本步骤………………………………………………………1.2 曲面矩阵的描述…………………………………………………………………1.2.1 网格和曲面图形的绘制…………………………………………………1.2.2 随机采样曲面图形数据…………………………………………………1.2.3 参数化曲面图形…………………………………………………………1.2.4 曲面图形透明处理………………………………………………………第2章三维MATLAB曲面色彩处理2.1 网格和曲面图形的着色………………………………………………………2.1.1 颜色映射表………………………………………………………………向量与色图矩阵2.1.2曲面曲率的颜色映射……………………………………………………2.2 曲面的光照处理…………………………………………………………………MATLAB中,三维图形的创建一般按照下面的步骤进行:(1)数据准备典型代码为:Z=peaks(20);(2)选定创建三维图形的窗口,并在窗口中确定图形绘制的区域典型代码为:figure(1)subplot(2,1,2)(3)调用三维图形函数典型代码为:h=surf(Z)(4)确定颜色映射方案和三维阴影算法典型代码为:colormap hotshading imterpset(h,’EdgeColor’,’k’)或添加灯光效果。
学士学位论文基于MATLAB的信道编译码系统设计毕业设计(论文)原创性声明和使用授权说明原创性声明本人郑重承诺:所呈交的毕业设计(论文),是我个人在指导教师的指导下进行的研究工作及取得的成果。
尽我所知,除文中特别加以标注和致谢的地方外,不包含其他人或组织已经发表或公布过的研究成果,也不包含我为获得及其它教育机构的学位或学历而使用过的材料。
对本研究提供过帮助和做出过贡献的个人或集体,均已在文中作了明确的说明并表示了谢意。
作者签名:日期:指导教师签名:日期:使用授权说明本人完全了解大学关于收集、保存、使用毕业设计(论文)的规定,即:按照学校要求提交毕业设计(论文)的印刷本和电子版本;学校有权保存毕业设计(论文)的印刷本和电子版,并提供目录检索与阅览服务;学校可以采用影印、缩印、数字化或其它复制手段保存论文;在不以赢利为目的前提下,学校可以公布论文的部分或全部内容。
作者签名:日期:学位论文原创性声明本人郑重声明:所呈交的论文是本人在导师的指导下独立进行研究所取得的研究成果。
除了文中特别加以标注引用的内容外,本论文不包含任何其他个人或集体已经发表或撰写的成果作品。
对本文的研究做出重要贡献的个人和集体,均已在文中以明确方式标明。
本人完全意识到本声明的法律后果由本人承担。
作者签名:日期:年月日学位论文版权使用授权书本学位论文作者完全了解学校有关保留、使用学位论文的规定,同意学校保留并向国家有关部门或机构送交论文的复印件和电子版,允许论文被查阅和借阅。
本人授权大学可以将本学位论文的全部或部分内容编入有关数据库进行检索,可以采用影印、缩印或扫描等复制手段保存和汇编本学位论文。
涉密论文按学校规定处理。
作者签名:日期:年月日导师签名:日期:年月日注意事项1.设计(论文)的内容包括:1)封面(按教务处制定的标准封面格式制作)2)原创性声明3)中文摘要(300字左右)、关键词4)外文摘要、关键词5)目次页(附件不统一编入)6)论文主体部分:引言(或绪论)、正文、结论7)参考文献8)致谢9)附录(对论文支持必要时)2.论文字数要求:理工类设计(论文)正文字数不少于1万字(不包括图纸、程序清单等),文科类论文正文字数不少于1.2万字。
摘要通信是信息远距离的传送,是人类生产和生活的主要支撑。
通信的目的是要把信息及时可靠地传送给对方,在数据通信过程中,衰损、失真、和噪声会使通信线路上的信号发生错误。
差错控制可以减少错误、提高通信质量,可以改善传输信道的电气特性,使误码率达到要求。
CRC(Cyclical Redundancy Checking)循环冗余校验码是一种重要的线性分组码,通过多项式除法检测错误,是在数据通信和数据检测中广泛应用的检错校验的循环码。
本设计研究了CRC循环冗余校验码的原理,以及利用C语言对其进行了编程和编译仿真,实现了CRC循环冗余校验码的编码及校验,在接收端收到通过校验的码,从而确定传输过程是否出错,得到的结论和理论上是一致的。
关键词:检错码;CRC循环冗余校验码;C语言前言随着科学技术的进步, 人们对信息传递的要求逐渐提高。
但在通信系统中, 可靠性与有效性是对矛盾, 要求有效性提高, 必然使每个码元所占的时间缩短, 从而受干扰和产生错误的可能性增大, 可靠性降低了; 要提高信息的可靠性,又使信息速率变慢有效性降低。
在实际信道上传输数字信号时,由于信道传输特性不理想及加性噪声的影响,所收到的数字信号不可避免的会发生错误。
为了加强通信系统的可靠性,除了合理设计基带信号,选择调制、解调方式,采用频域均衡、时域均衡之外,还需要采用信道编码,即差错控制编码,使误码率进一步降低,来满足指标要求。
循环冗余校验码CRC(Cyclical Redundancy Checking)是目前通信系统中最常用的一种差错控制编码。
循环冗余校验码是一种高效率且可靠的方法, 由线性分组码分支而来的, 是一种通过多项式除法检测错误的很不寻常而又巧妙的方法, 一方面它有很强的检测能力, 二是它的编码器电路及错误检测器电路都很容易实现, 它的优点使它在通信系统中得到了广泛的应用。
利用CRC进行检错的过程可简单描述为:在发送端根据要传送的二进制码序列,以一定的规则产生一个校验用的监督码(CRC码),附在原始信息后边,构成一个新的二进制码序列数,然后发送出去。
目录TOC \o "1-3" \h \u HYPERLINK \l _Toc6750 前言.... PAGEREF _Toc6750 1HYPERLINK \l _Toc26804 工程概况................ PAGEREF _Toc26804 1HYPERLINK \l _Toc14622 正文.................... PAGEREF _Toc14622 2 HYPERLINK \l _Toc4430 3.1设计的目的和意义... PAGEREF _Toc4430 2HYPERLINK \l _Toc31075 3.1.1设计的目的. PAGEREF _Toc31075 2HYPERLINK \l _Toc18535 3.1.2设计的意义. PAGEREF _Toc18535 2 HYPERLINK \l _Toc31236 3.2 线性分组码的编码与译码原理 PAGEREF _Toc31236 2 HYPERLINK \l _Toc11233 3.2.1线性分组码的编码原理 PAGEREF _Toc11233 2HYPERLINK \l _Toc6682 3.2.2 线性分组码的译码原理 PAGEREF _Toc6682 3 HYPERLINK \l _Toc31791 3.3 2PSK的调制与解调原理 PAGEREF _Toc31791 4 HYPERLINK \l _Toc26402 3.3.1调制的原理. PAGEREF _Toc26402 4HYPERLINK \l _Toc27747 3.3.2解调的原理. PAGEREF _Toc27747 4 HYPERLINK \l _Toc23880 3.4 不同信噪比是的测试结果 PAGEREF _Toc23880 5 HYPERLINK \l _Toc20433 3.4.1 信噪比为1时 PAGEREF _Toc20433 5HYPERLINK \l _Toc4861 3.4.2 信噪比为5时. PAGEREF _Toc4861 5HYPERLINK \l _Toc31183 3.4.3 信噪比为10时 PAGEREF _Toc31183 6HYPERLINK \l _Toc29253 3.4.4译码时当检测到错码结果如图 PAGEREF _Toc29253 6 HYPERLINK \l _Toc2127 致谢...................... PAGEREF _Toc2127 7HYPERLINK \l _Toc30045 参考文献................ PAGEREF _Toc30045 7前言近年来,随着计算机、卫星通信及高速数据网的飞速发展,数据的交换、数据的交换理和存储技术得到了广泛的应用,人们对数据传输和存储系统的可靠性提出了越来越高的要求。
因此,如何控制差错、提高数据传输和存储的可靠性,成为现代数字通信系统设计的重要课题。
目前,绝大多数的数字计算机和数字通信系统中广泛采用二进制形式的码。
而线性分组码具有编译码简单,封闭性好等特点,采用差错控制编码技术是提高数字通信可靠性的有效方法,是目前较为流行的差错控制编码技术。
本课程设计主要讨论数字通信系统中的信道编码中的线性分组码的编译码以及2PSK调制、解调。
分组码是一组固定长度的码组,可表示为(n,k),通常它用于前向纠错。
在分组码中,监督位被加到信息位之后,形成新的码。
在编码时,k个信息位被编为n位码组长度,而n-k个监督位的作用就是实现检错与纠错。
对于长度为n的二进制线性分组码,它有种2n可能的码组,从2n种码组中,可以选择M=2k 个码组(k<n)组成一种码。
调制在时域上是用一个低频信号对一高频信号某一特征参量进行的控制。
低频信号称为调制信号,高频信号称为载波,而调制出来的信号称为已调信号,所以调制的过程在时域就是使载波的某一特征参量随调制信号的变化而变化的过程。
调制过程在频域上是一个移频的过程。
解调,调制的逆过程,即从已调波中不失真地恢复原有的低频调制信号的过程。
解调的方法可分为两类:相干解调(同步检波)和非相干解调(包络检波)。
本课程设计主要是采用Matlab仿真实现线性分组码的编译码和2PSK的调制与解调。
在加深理论知识的基础上,对Matlab仿真也有进一步的理解。
工程概况本次课程设计的主题是采用Matlab软件仿真实现线性分组码的仿真与分析。
首先要求对Matlab软件有着较为深入地了解和认识,掌握一些Matlab软件的基本函数用法。
例如:用Matlab 软件实现2PSK的调制与解调等等。
同时利用软Matlab件也能对书本上的知识进行验证,,与书本上的讲解进行对照分析和比较。
本次课程设计要求的技术对我们通信的学习起着很大的作用。
正文3.1设计的目的和意义3.1.1设计的目的1、学会查阅资资料。
2、掌握线性分组码的编码原理、编码步骤和译码方法。
3、熟悉Matlab软件的基本操作,学会用Matlab软件进行线性分组码的编码和译码。
3.1.2设计的意义通过本课程设计实验使我们掌握了Matlab的基本使用方法。
培养了我们的实际应用的能力,提高分析问题、解决问题的能力。
而且提高我们对这门课的了解深度,把理论知识和实践仿真相结合,增强了个人的动手和独立思考能力,也为以后后续课程的学习以及从事实际工作打下良好的基础。
3.2 线性分组码的编码与译码原理3.2.1线性分组码的编码原理对于码组长度为n、信息码元为k位、监督码元为r=n-k位的分组码,常记作(n,k)码,如果满足2r-1≥n,则有可能构造出纠正一位或一位以上错误的线性码。
设分组码(n,k)中,k = 11,为能纠正一位误码,要求r≥3。
现取r=4,则n=k+r=15。
该例子中,信息组为:(c14c13c12c11c10c9c8c7c6c5)码字为:(c14c13c12c11c10c9c8c7c6c5c4c3c2c1c0)。
一个系统码的生成矩阵G,其左边k行k列应是一个k阶单位方阵Ik,因此生成矩阵G表示为:G=[Ik P]由H矩阵得到(n,k)线性分组码的每一码字ci,(i=1,2,…,2k),都必须满足由H矩阵各行所确定的线性方程组,即 ci·HT=0.(15,11)码的生成矩阵G中每一行及其线性组合都是(n,k)码的码字,所以有G·HT =0。
由G和H构成的行生成的空间互为零空间,即G和H彼此正交。
H=[PT Ir]其右边r行r列组成一个单位方阵。
本文中采用的是(15,11)的线性分组码,线性分组码的编码由监督矩阵和生成矩阵实现。
监督矩阵H为(4×11)的矩阵,由监督方程和(4×4)的单位矩阵构成,生成矩阵G为(11×15)的矩阵,由(11×11)的单位矩阵和监督矩阵的转置矩阵构成。
编程时具体实现方法如下:= 1 \* GB3 ①将要编码的序列先整形,整为11列。
= 2 \* GB3 ②如果序列不能被11整除在后边补0使其能被11整除。
= 3 \* GB3 ③将整形后的序列与生成矩阵G相乘即得到编码后的码字。
3.2.2 线性分组码的译码原理两个码字之间,对应位取之不同的个数,称为汉明距离,用d表示。
一个吗的最小距离dmin 定义为dmin=min{d(ci,cj),i≠j,ci,cj∈(n,k)},两个码字之间的距离表示了它们之间差别的大小。
距离越大,两个码字的差别越大,则传送时从一个码字错成另一码字的可能性越小。
码的最小距离愈大,其抗干扰能力愈强。
对于任一个(n,k)线性分组码,若要在码字内检测出e个错误,则要求码的最小距离d≥e+1; 纠正t个错误,则要求码的最小距离d≥2t+1;(3)纠正t个错误同时检测e(≥t)个错误,则要求 d≥t+e+1。
假设接收端收到的码字为B,那么它和原来发送端发送的码字A之间就有可能存在着误差。
即在码组A={ a14 a13 a12 a11 a10 a9 a8 a7 a6 a5 a4 a3 a2 a1 a0 }中的任意一位就有可能出错。
这样我们在接收端接收到一个码组时就有可能判断错发送端原来应该要表达的意思。
为了描述数据在传输信道中出现错误的情况,引入了错误图样E,在错误图样中,0代表对应位没有传错,1代表传输错误。
实际上错误图样E就是收序列与发送序列的差。
所以在译码中用接收到的码字B模尔加错误图样E就可以得到发送端的正确码字A。
因此译码的过程就是要找到错误图样E。
定义:校正子SS = B * H EMBED Equation.3 = ( A + E ) * H EMBED Equation.3= A * H EMBED Equation.3 + E * H EMBED Equation.3 = E * H EMBED Equation.3因为A是编得的正确码字。
根据前面所叙述,它和监督矩阵的转置相乘为0。
显然,S仅与错误图样有关,它们之间是一一对应的关系。
找到了校正子S,也就可以找到E。
而与发送的码字无关。
若E=0,则S=0;因此根据S是否为0可进行码字的检错。
如果接收码字B中只有一位码元发生错误,又设错误在第i位。
即Ei-1=1,其他的Ei均为0。
在后面的译码程序中,建立了一个校正子S与错误图样E对应的表。
也就是收到一个B序列,就可以通过计算得到一个校正子,而每一个校正子都对应着一个错误图样E,再通过B模尔加上E,就可以得到正确的码字A。
因为在不同的错误序列B中,同一位码元错误时对应的E是一样的,所以可以利用00000000000这个正确的码字让它每位依次错误,来求得它的校正子。
而这时的矩阵B就是错误图样E。
在编程时本实验所采用的为(15,11)线性分组码,最小汉明距离为3,所以具有纠错1位检错两位的功能。
编程时具体实现方法如下:(设一个接收码字矩阵为R,R*H'=S (模2乘),则S为码字对应的伴随式矩阵如果S=0则说明接受码字无差错;(如果S不为0,查看矩阵S中不为0的那行所在行数,该行即收码字错误所在行i;(将S转置,将不为0的一列与H每一列进行比较,找到H中相同列,该列的列数即为错误所在列;④由步骤((得到错误具体位置,模2加对应的错误图样就可得到正确码字。
3.3 2PSK的调制与解调原理3.3.1调制的原理数字调制有三种基本调制方式:振幅键控(ASK)、频移键控(FSK)和相移键控(PSK或DPSK)。
2PSK调制利用载波的相位变化来传递数字信息,振幅和频率保持不变。
双极性的全占空矩形脉冲序列与正弦载波相乘就得到调制信号。
因此进行调制时首先进行码形变换变为双极性的,再经乘法器与载波相乘得到调制信号。