2019年中考数学总复习第六单元圆课时训练27圆的有关概念与性质练习

课时训练(二十七)圆的有关性质(限时:30分钟)|夯实基础|1.下列四个命题:①直径所对的圆周角是直角;②圆既是轴对称图形,又是中心对称图形;③在同圆中,相等的圆周角所对的弦相等;④三点确定一个圆.其中正确命题的个数为()A.1B.2C.3D.42.若☉O的半径是5,点A到圆心O的距离是7,则点A与☉O的位置关系是()A.点A在☉O上B.点A在☉O内C.点A在☉O外D.点A与圆心O重合3.[2017·永州]小红不小心把家里的一块圆形玻璃镜打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图K27-1所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是()图K27-1A.AB,AC边上的中线的交点B.AB,AC边上的垂直平分线的交点22C .AB ,AC 边上的高所在直线的交点D .∠BAC 与∠ABC 的角平分线的交点4.[2018·聊城] 如图K27-2,☉O 中,弦BC 与半径OA 相交于点D ,连接AB ,OC.若∠A=60°,∠ADC=85°,则∠C 的度数是()图K27-2A .25°B .27.5°C .30°D .35°5.[2018·邵阳] 如图K27-3所示,四边形ABCD 为☉O 的内接四边形,∠BCD=120°,则∠BOD 的大小是 ()图K27-3A .80°B .120°C .100°D .90°6.[2018·枣庄] 如图K27-4,AB 是☉O 的直径,弦CD 交AB 于点P ,AP=2,BP=6,∠APC=30°,则CD 的长为 ()图K27-4A. B .2C .2D .87.[2017·大连]如图K27-5,在☉O中,弦AB=8 cm,OC⊥AB,垂足为C,OC=3 cm,则☉O的半径为cm.图K27-58.如图K27-6,已知AB是☉O的弦,半径OC垂直于AB,点D是☉O上一点,且点D与点C位于弦AB两侧,连接AD,CD,OB,若∠BOC=68°,则∠ADC= 度.图K27-69.[2017·北京]如图K27-7,AB为☉O的直径,C,D为☉O上的点,=,若∠CAB=40°,则∠CAD= .图K27-710.[2017·西宁]如图K27-8,四边形ABCD内接于☉O,点E在BC的延长线上,若∠BOD=120°,则∠DCE= .图K27-811.[2018·黄冈]如图K27-9,△ABC内接于☉O,AB为☉O的直径,∠CAB=60°,弦AD平分∠CAB,若AD=6,则AC= .344图K27-912.[2018·绥化] 如图K27-10,一下水管道横截面为圆形,直径为100 cm,下雨前水面宽为60 cm,一场大雨过后,水面宽为80 cm,则水位上升了 cm .图K27-1013.如图K27-11,已知△ABC ,以AB 为直径的☉O 分别交AC 于D ,BC 于E ,连接ED ,若ED=EC.图K27-11(1)求证:AB=AC ; (2)若AB=4,BC=2,求CD 的长.14.[2017·苏州改编]如图K27-12,已知△ABC内接于☉O,AB是直径,点D在☉O上,OD∥BC,过点D作DE⊥AB,垂足为E,连接CD交OE于点F.图K27-12(1)求证:△DOE∽△ABC;(2)求证:∠ODF=∠BDE.|拓展提升|15.[2018·湘潭]如图K27-13,AB是以O为圆心的半圆的直径,半径CO⊥AO,点M 是上的动点,且不与点A,C,B重合,直线AM交直线OC于点D,连接OM与CM.(1)若半圆的半径为10;①当∠AOM=60°时,求DM的长;566②当AM=12时,求DM 的长.(2)探究:在点M 运动的过程中,∠DMC 的大小是否为定值?若是,求出该定值;若不是,请说明理由.图K27-13参考答案1.C2.C[解析] ∵☉O的半径是5,点A到圆心O的距离是7,即点A到圆心O的距离大于圆的半径,∴点A在☉O外.3.B[解析] 本题实质上是要确定三角形外接圆的圆心,三角形外接圆的圆心是三边垂直平分线的交点,故选B.4.D[解析] ∵∠A=60°,∠ADC=85°,∴∠B=∠ADC-∠A=85°-60°=25°,∴∠O=2∠B=2×25°=50°,∴∠C=∠ADC-∠O=85°-50°=35°.5.B[解析] 根据“圆内接四边形的对角互补”可得∠BCD+∠A=180°,因为∠BCD=120°,所以∠A=60°.又根据“在同圆中,同弧所对的圆心角等于圆周角的2倍”,所以∠BOD=2∠A=120°.故选B.6.C[解析] 过点O作OE⊥CD于E,连接OC.∵AP=2,BP=6,∴AB=8,∴OA=OB=4,∴OP=2,∵∠APC=30°,∴OE=OP=1.在Rt△OCE中,CE==.∵OE⊥CD,O是圆心,∴CD=2CE=2.故选C.7.5[解析] 由于在☉O中,弦AB=8 cm,OC⊥AB,所以BC=AB=4 cm.连接OB,则OB===5(cm),故答案为5.7888.34 [解析] 如图,连接OA.∵OC ⊥AB ,∴=,∴∠AOC=∠COB=68°,∴∠ADC=∠AOC=34°.9.25° [解析] 连接BC ,BD ,∵AB 是☉O 的直径,C ,D 为☉O 上的点,∴∠ACB=90°.∵∠CAB=40°,∴∠CBA=50°.∵=,∴∠CBD=∠DBA=∠CBA=25°, ∴∠CAD=∠CBD=25°.10.60° [解析] ∵∠BOD=120°,∴∠BAD=60°,又∠BAD+∠BCD=180°,∠DCE+∠BCD=180°,∴∠DCE=∠BAD=60°. 11.2[解析] 连接BD ,因为∠CAB=60°,弦AD 平分∠CAB ,所以∠DAB=30°,因为AB 是☉O 的直径,所以∠C=∠D=90°,所以AB==4,因为∠C=90°,∠CAB=60°,所以∠ABC=30°,所以AC=AB ·sin30°=2.12.10或70 [解析] 作OD ⊥AB 于C ,OD 交☉O 于点D ,连接OB,9由垂径定理得:BC=AB=30 cm, 在Rt △OBC 中,OC==40(cm),当水位上升到圆心以下且水面宽80 cm 时,圆心到水面距离==30(cm),水面上升的高度为:40-30=10(cm);当水位上升到圆心以上且水面宽80 cm 时,水面上升的高度为:40+30=70(cm), 综上可得,水面上升的高度为10 cm 或70 cm . 故答案为10或70.13.解:(1)证明:∵ED=EC ,∴∠EDC=∠C.∵∠EDC=∠B ,∴∠B=∠C ,∴AB=AC.(2)连接AE,∵AB 为直径,∴AE ⊥BC ,由(1)知AB=AC ,∴BE=CE=BC=.∵四边形ABED 为☉O 的内接四边形, ∴∠CED=∠BAC.又∵∠C=∠C ,∴△CED ∽△CAB ,∴=,∴CE ·CB=CD ·CA ,∵AC=AB=4,1010∴×2=4CD ,∴CD=.14.证明:(1)∵AB 是☉O 的直径,∴∠ACB=90°.∵DE ⊥AB ,∴∠DEO=90°,∴∠DEO=∠ACB. ∵OD ∥BC ,∴∠DOE=∠ABC , ∴△DOE ∽△ABC.(2)∵△DOE ∽△ABC ,∴∠ODE=∠A.∵∠A 和∠BDC 都是所对的圆周角, ∴∠A=∠BDC ,∴∠ODE=∠BDC. ∴∠ODF=∠BDE.15.[解析] (1)①当∠AOM=60°时,∠D=30°,△AMO 为等边三角形,然后根据含有30°角的直角三角形的性质得到AD=2AO ,再结合△AMO 为等边三角形求出DM 的长;②连接BM ,则可得∠AMB=90°,根据两个角分别对应相等的三角形是相似三角形得到△AOD ∽△AMB ,从而得到=,求出AD 的长,进而求出DM 的长;(2)在图①中,由于AB 是直径,所以∠AMB=90°,所以∠DMC+∠CMB=90°,然后根据所对的圆心角与圆周角的关系得到∠CMB=∠COB ,从而得到∠DMC 的度数为45°,是一个定值;在图②中,∠DMC=∠AOC=45°,从而得到∠DMC 的度数仍然是一个定值. 解:(1)①当∠AOM=60°时,∵OM=OA ,∴△AMO 是等边三角形, ∴∠A=∠MOA=60°,AM=AO=10. ∵CO ⊥AO , ∴∠D=30°, ∴AD=2AO=20,11∴DM=AD-AM=10.②连接MB ,∵AB 是直径,∴∠AMB=90°,∵CO ⊥AO ,∴∠AOD=90°,∵∠A=∠A ,∴△ADO ∽△ABM ,∴=,∵AO=10,AM=12,∴AD=,∴DM=AD-AM=.(2)∠DMC 的大小是定值.当点M 位于之间时,连接BM ,如图:∵AB 是直径,∴∠AMB=90°,∴∠DMC+∠CMB=90°.∵∠CMB=∠COB=45°,∴∠DMC=45°.当点M 位于之间时,∠DMC=∠AOC=45°.综上所述,∠DMC=45°,是定值.百度文库是百度发布的供网友在线分享文档的平台。

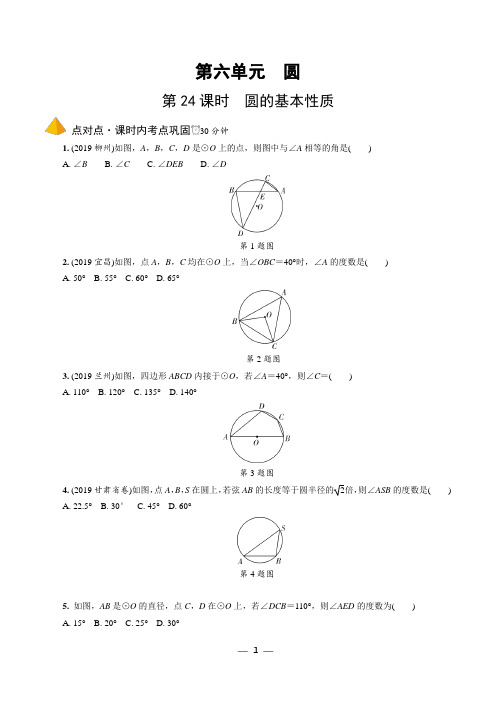
第六单元圆第24课时圆的基本性质点对点·课时内考点巩固30分钟1. (2019柳州)如图，A，B，C，D是⊙O上的点，则图中与∠A相等的角是()A. ∠BB. ∠CC. ∠DEBD. ∠D第1题图2. (2019宜昌)如图，点A，B，C均在⊙O上，当∠OBC＝40°时，∠A的度数是()A. 50°B. 55°C. 60°D. 65°第2题图3. (2019兰州)如图，四边形ABCD内接于⊙O，若∠A＝40°，则∠C＝()A. 110°B. 120°C. 135°D. 140°第3题图4. (2019甘肃省卷)如图，点A，B，S在圆上，若弦AB的长度等于圆半径的2倍，则∠ASB的度数是()A. 22.5°B. 30°C. 45°D. 60°第4题图5.如图，AB是⊙O的直径，点C，D在⊙O上，若∠DCB＝110°，则∠AED的度数为()A. 15°B. 20°C. 25°D. 30°第5题图6. (2019西安高新一中模拟)如图，四边形ABCD 内接于⊙O ，AD ∥BC ，∠DAB ＝48°，则∠AOC 的度数是( )A. 48°B. 96°C. 114°D. 132°第6题图7. (2019陕西黑马卷)如图，在⊙O 中，弦AB ∥CD ，连接BC ，OA ，OD .若∠BCD ＝25°，CD ＝OD ，则∠AOD 的度数是( )A. 140°B. 120°C. 110°D. 100°第7题图8. (2019赤峰)如图，AB 是⊙O 的弦，OC ⊥AB 交⊙O 于点C ，点D 是⊙O 上一点，∠ADC ＝30°，则∠BOC 的度数为( )A. 30°B. 40°C. 50°D. 60°第8题图9. (2019贵港)如图，AD 是⊙O 的直径，AB ︵＝CD ︵，若∠AOB ＝40°，则圆周角∠BPC 的度数是( ) A. 40° B. 50° C. 60° D ．70°第9题图10. 如图，△ABC 内接于⊙O ，∠BAC ＝120°，AB ＝AC ，BD 为⊙O 的直径，AD ＝6，则BD 的长为( ) A. 3 B. 2 3 C. 4 3 D. 12第10题图11. 如图，AB 为⊙O 的直径，∠CAB ＝30°，CB ＝3，∠ACB 的平分线CD 交⊙O 于点D ，则弦AD 的长为( )A. 2 3B. 2 2C. 3 3D. 3 2第11题图12. 如图，B 、C 是⊙A 上的两点，AB 的垂直平分线与⊙A 交于E 、F 两点，与线段AC 交于点D ，连接BC 、BD 、BF 、CF .若∠BFC ＝20°，则∠DBC ＝( )A. 30°B. 29°C. 28°D. 20°第12题图13. (2019西工大附中模拟)如图，已知△ABC 内接于⊙O ，EF 为⊙O 的直径，且点F 是弧BC ︵的中点．若∠B ＝40°，∠C ＝60°，则∠AFE 的度数为( )A. 10°B. 20°C. 30°D. 40°第13题图14. (2019西安铁一中模拟)如图，在半径为3的⊙O中，弦BC、DE所对的圆周角分别是∠A、∠F，且∠A＋∠F＝90°.若BC＝4，则DE的长为()A. 13B. 4C. 5D. 2 5第14题图15.在圆内接四边形ABCD中，∠ACB＝∠ACD＝60°，对角线AC、BD交于点E.已知BC＝32，CD ＝22，则线段CE的长为()第15题图A. 32 2B. 7 5C. 62 5D. 22 316. (2019株洲)如图所示，AB为⊙O的直径，点C在⊙O上，且OC⊥AB，过点C的弦CD与线段OB 相交于点E，满足∠AEC＝65°，连接AD，则∠BAD＝________度．第16题图17.(2019安徽)如图，△ABC内接于⊙O，∠CAB＝30°，∠CBA＝45°，CD⊥AB于点D，若⊙O的半径为2，则CD的长为________．第17题图18.已知半径为5的⊙O中，弦AB＝52，弦AC＝5，则∠BAC的度数是________．点对线·板块内考点衔接10分钟1. (2019襄阳)如图，AD是⊙O的直径，BC是弦，四边形OBCD是平行四边形，AC与OB相交于点P，下列结论错误的是()A. AP＝2OPB. CD＝2OPC. OB⊥ACD. AC平分OB第1题图2. (2019西工大附中模拟)如图，已知⊙O的内接五边形ABCDE，连接BE、CE，若AB＝BC＝CE，∠EDC ＝130°，则∠ABE的度数为()A. 25°B. 30°C. 35°D. 40°第2题图3.(2019天水)如图，四边形ABCD是菱形，⊙O经过点A、C、D，与BC相交于点E，连接AC、AE.若∠D＝80°，则∠EAC的度数为()A. 20°B. 25°C. 30°D. 35°第3题图4.(2019柳州)在半径为5的圆形纸片上裁出一个边长最大的正方形纸片，则这个正方形纸片的边长应为________．5.如图，在矩形ABCD中，AB＝3，BC＝4，O为矩形ABCD的中心，以D为圆心，1为半径作⊙D，P为⊙D上的一个动点，连接AP、OP、OA，则△AOP面积的最大值为________．第5题图点对面·跨板块考点迁移2分钟1. (2019安顺)如图，半径为3的⊙A经过原点O和点C(0，2)，B是y轴左侧⊙A优弧上一点，则tan∠OBC 为()第1题图A. 13 B. 22 C.223 D.24参考答案第24课时 圆的基本性质点对点·课时内考点巩固1. D 【解析】在⊙O 中，∵∠A 与∠D 都是BC ︵所对的圆周角，∴∠A ＝∠D .2. A 【解析】∵OB ＝OC ，∴∠OCB ＝∠OBC ＝40°.∴在△OBC 中，∠BOC ＝180°－∠OCB －∠OBC ＝180°－40°－40°＝100°.∴∠A ＝12∠BOC ＝12×100°＝50°.3. D 【解析】∵四边形ABCD 内接于⊙O ，∠A ＝40°，∴∠C ＝180°－∠A ＝140°.4. C 【解析】如解图，设圆心为O ，半径为r ，则AB ＝2r .连接OA 、OB ，则r 2＋r 2＝(2r )2，∴△OAB 为等腰直角三角形，∠AOB ＝90°.∴∠ASB ＝12∠AOB ＝45°.第4题解图5. B 【解析】如解图，连接AC ，∵AB 为直径，∴∠ACB ＝90°，∴∠ACD ＝∠DCB －∠ACB ＝110°－90°＝20°，∴∠AED ＝∠ACD ＝20°.第5题解图6. B 【解析】∵AD ∥BC ，∴∠B ＝180°－∠DAB ＝132°，∵四边形ABCD 内接于⊙O ，∴∠D ＝180°－∠B ＝48°，由圆周角定理得，∠AOC ＝2∠D ＝96°.7. C 【解析】如解图，连接OC ，∵AB ∥CD ，∴∠B ＝∠BCD ＝25°，∴∠AOC ＝50°，∵CD ＝OD ，OD ＝OC ，∴OC ＝OD ＝CD ，∴△COD 为等边三角形，∴∠COD ＝60°，∴∠AOD ＝∠AOC ＋∠COD ＝110°.第7题解图8. D 【解析】∵OC ⊥AB ，∴点C 是AB ︵的中点，即AC ︵＝BC ︵.∴∠BOC ＝∠AOC ＝2∠ADC ＝60°.9. B 【解析】∵AB ︵＝CD ︵，∴∠COD ＝∠AOB ＝40°，∴∠BOC ＝100°，∴∠BPC ＝12∠BOC ＝50°.10. C 【解析】∵∠BAC ＝120°，AB ＝AC ，∴∠BCA ＝12×(180°－120°)＝30°.∴∠D ＝∠BCA ＝30°.∵BD为⊙O 的直径，∴∠BAD ＝90°.在Rt △BAD 中，BD ＝AD cos30°＝632＝4 3. 11. D 【解析】如解图，连接BD ，∵AB 为⊙O 的直径，∴∠ACB ＝∠ADB ＝90°，在Rt △ABC 中，∵∠CAB ＝30°，∴AB ＝2CB ＝6，∵CD 平分∠ACB ，∴∠BCD ＝45°，∵∠BAD ＝∠BCD ＝45°，∴△ABD 为等腰直角三角形，∴AD ＝22AB ＝22×6＝3 2.第11题解图12. A 【解析】∵∠BFC ＝20°，∴∠BAC ＝2∠BFC ＝40°，∵AB ＝AC ，∴∠ABC ＝∠ACB ＝12(180°－40°)＝70°.又∵EF 是线段AB 的垂直平分线，∴AD ＝BD ，∴∠ABD ＝∠BAC ＝40°，∴∠DBC ＝∠ABC －∠ABD ＝70°－40°＝30°.13. A 【解析】如解图，连接OC 、CF .∵∠B ＝40°，∠ACB ＝60°，∴∠BAC ＝80°，∠AFC ＝∠ABC ＝40°，∵点F 是弧BC ︵的中点，∴∠BAF ＝∠CAF ＝40°，∴∠COF ＝2∠CAF ＝80°，∵OF ＝OC ，∴∠OFC ＝12(180°－80°)＝50°，∴∠AFE ＝∠OFC －∠AFC ＝10°.第13题解图14. D 【解析】如解图，连接DO 并延长，交⊙O 于点G ，连接EG 、FG ，则∠DFG ＝∠DEG ＝90°，又∵∠A ＋∠DFE ＝90°，∠GFE ＋∠DFE ＝90°，∴∠A ＝∠GFE .则GE ＝BC ＝4.∵⊙O 的半径为3，∴DG ＝6.在Rt △DEG 中，DE ＝DG 2－GE 2＝62－42＝2 5.第14题解图15. C 【解析】如解图，作BM ⊥AC 于点M ，DN ⊥AC 于点N ，则BM ∥DN ，∴△BME ∽△DNE ，∴MENE ＝BM DN ，∵∠ACB ＝∠ACD ＝60°，∴∠CBM ＝∠CDN ＝30°，∴CM ＝12BC ＝322，CN ＝12CD ＝2，∴BM ＝3CM ＝362，DN ＝3CN ＝6，∴MN ＝CM －CN ＝122，∴ME NE ＝32，∴EN ＝25MN ＝25，∴CE ＝CN ＋EN ＝2＋25＝625.第15题解图16. 20 【解析】∵AB 为⊙O 的直径，点C 在⊙O 上，且OC ⊥AB ，∴∠ADC ＝12∠AOC ＝45°.∵∠AEC＝65°，且∠AEC 是△ADE 的一个外角，∴∠BAD ＝∠AEC －∠ADC ＝20°.17. 2 【解析】如解图，连接OA 、OC ，∵∠CBA ＝45°，∴∠AOC ＝90°.又∵OA ＝OC ＝2，∴AC ＝2 2.在Rt △ACD 中，∠CDA ＝90°，∠CAD ＝30°，∴CD ＝AC ·sin30°＝ 2.第17题解图18. 105°或15° 【解析】如解图，连接OC ，OA ，OB .∵OC ＝OA ＝AC ＝5，∴△OAC 是等边三角形，∴∠CAO ＝60°，∵OA ＝OB ＝5，AB ＝52，∴OA 2＋OB 2＝AB 2，∴△OAB 是等腰直角三角形，∠OAB ＝45°，点C 的位置有两种情况，如解图①时，∠BAC ＝∠CAO ＋∠OAB ＝60°＋45°＝105°；如解图②时，∠BAC ＝∠CAO －∠OAB ＝60°－45°＝15°.综上所述，∠BAC 的度数是105°或15°.第18题解图点对线·板块内考点衔接1. A 【解析】如解图，连接OC .∵四边形OBCD 是平行四边形，OD ＝OB ，∴四边形OBCD 是菱形．∴OD ＝OC ＝CD .∵AD 是⊙O 的直径，∴∠ACD ＝90°.∵CD ∥OB ，∴CD ＝2OP ，OB ⊥AC .故B 、C 选项正确．∵△CBP ≌△COP (HL)，∴BP ＝OP .故D 选项正确．第1题解图2. B 【解析】如解图，连接OA ，OB ，OC ，OE ，∵AB ＝BC ＝CE ，∴AB ︵＝BC ︵＝CE ︵，∠1＝∠2＝∠3，在四边形BCDE 中，∵∠D ＝130°，∴∠CBE ＝50°，∠2＝2∠CBE ＝100°，∴∠1＝∠3＝∠2＝100°，∠AOE ＝360°－3×100°＝60°，∴∠ABE ＝12∠AOE ＝30°.第2题解图3. C 【解析】∵∠AEB ＋∠AEC ＝∠D ＋∠AEC ＝180°，∠D ＝80°，∴∠AEB ＝∠D ＝80°.∵四边形ABCD 是菱形，∴∠B ＝∠D ＝80°，AB ＝BC ，∴∠B ＝∠AEB .∴∠BAE ＝180°－2∠B ＝20°，∠BAC ＝∠ACB ＝12(180°－∠B )＝50°.∴∠EAC ＝∠BAC －∠BAE ＝30°.4. 52 【解析】如解图，四边形ABCD 为正方形，BD 为⊙O 的直径，OA 为半径，则OA ＝OB ＝5，OA ⊥OB ，∴AB ＝OA 2＋OB 2＝52＋52＝5 2.第4题解图5.174【解析】如解图，延长AO 至C 点，过点D 作DF ⊥AC 于点F ，延长FD 交⊙D 于点P ′，连接AP ′，OP ′，要使△AOP 面积最大，则只需AO 边上的高最大，此时P ′满足条件，即P ′F 为△AOP 的AO 边上最大的高．∵DF ＝AD ·CD AC ＝4×342＋32＝125，∴P ′F ＝DF ＋DP ′＝125＋1＝175，AO ＝12AC ＝52，∴△AOP 的最大面积为12AO ·P ′F ＝12×52×175＝174.第5题解图点对面·跨板块考点迁移1. D 【解析】如解图，连接AC 、AO ，得到等腰三角形AOC ，过A 点作AD ⊥OC ，垂足为点D ，∴∠CAD ＝12∠CAO ＝∠OBC ，∵点C 坐标为(0，2)，∴CD ＝OD ＝1，∴在Rt △ACD 中，AD ＝AC 2－CD 2＝32－12＝22，∴tan ∠OBC ＝tan ∠CAD ＝CD AD ＝122＝24.第1题解图第六单元 圆第25课时 与圆有关的位置关系点对点·课时内考点巩固30分钟1. (2019广州)平面内，⊙O 的半径为1，点P 到O 的距离为2，过点P 可作⊙O 的切线的条数为( ) A. 0条 B. 1条 C. 2条 D. 无数条2. (2019重庆B 卷)如图，AB 是⊙O 的直径，AC 是⊙O 的切线，A 为切点，若∠C ＝40°，则∠B 的度数为( )第2题图A. 60°B. 50°C. 40°D. 30° 点对线·板块内考点衔接60分钟1. (2019哈尔滨)如图，P A 、PB 分别与⊙O 相切于A 、B 两点，点C 为⊙O 上一点，连接AC 、BC ，若∠P ＝50°，则∠ACB 的度数为( )A. 60°B. 75°C. 70°D. 65°第1题图2. (2019舟山)如图，已知⊙O 上三点A ，B 、C ，半径OC ＝1，∠ABC ＝30°，切线P A 交OC 延长线于点P ，则P A 的长为( )A. 2B. 3C. 2D. 1 2第2题图3.如图，AB是⊙O的直径，P A切⊙O于点A，连接PO并延长交⊙O于点C，连接AC.若AB＝10，∠P ＝30°，则AC的长度是()A. 5 3B. 5 2C. 5D. 5 2第3题图4. (2019泰安)如图，△ABC是⊙O的内接三角形，∠A＝119°，过点C的圆的切线交BO于点P，则∠P 的度数为()A. 32°B. 31°C. 29°D. 61°第4题图5. (北师九下P92例2题改编)如图，边长为23的等边△ABC的内切圆的半径为()A. 1B. 3C. 2D. 2 3第5题图6. (2019贺州)如图，在△ABC中，O是AB边上的点，以O为圆心，OB为半径的⊙O与AC相切于点D，BD平分∠ABC，AD＝3OD，AB＝12，CD的长是()A. 2 3B. 2C. 3 3D. 4 3第6题图7.如图，AB是⊙O的直径，点C在BA的延长线上，直线CD与⊙O相切于点D，弦DF⊥AB于点E，连接BD.若CD＝BD＝43，则OE的长度为()第7题图A. 3B. 2C. 2 3D. 48. (2018益阳)如图，在圆O中，AB为直径，AD为弦，过点B的切线与AD的延长线交于点C，AD＝DC，则∠C＝________度．第8题图9.(2019南京)如图，P A、PB是⊙O的切线，A、B为切点，点C、D在⊙O上．若∠P＝102°，则∠A ＋∠C＝________°.第9题图10. (2019眉山)如图，在Rt△AOB中，OA＝OB＝42，⊙O的半径为2，点P是AB边上的动点，过点P作⊙O的一条切线PQ(点Q为切点)，则线段PQ长的最小值为________．第10题图11.(2019陕师大附中模拟)如图，已知点E在直角△ABC的斜边AB上，以AE为直径的⊙O与直角边BC相切于点D.(1)求证：AD平分∠BAC；(2)若BE＝2，BD＝4，求⊙O的半径．第11题图12.如图，MP与⊙O相切于点M，连接PO并延长，交⊙O于点A、B，弦AC∥MP，连接OM、BC、CM.(1)求证：OM∥BC；(2)若∠P＝30°，求证：四边形BCMO为菱形．第12题图13.如图，AB为⊙O的直径，AD、BE为⊙O的弦，延长AD、BE交于点C，且AB＝AC，过点B作⊙O的切线交AC 的延长线于点F .(1)求证：BE ＝CE ；(2)若BF ＝4，CF ＝2，求AD 的长．第13题图14. (2019西安交大附中模拟)如图，在△ABC 中，∠ACB ＝90°，点D 是AB 的中点，以AD 为直径的⊙O 交AC 于点E ，⊙O 的切线EF 交CD 于点F .(1)求证：EF ⊥CD ；(2)若AC ＝10，cos A ＝56，求线段DF 的长．第14题图15. (2019黄冈改编)如图，Rt △ABC 中，∠ACB ＝90°，以AC 为直径的⊙O 交AB 于点D ，过点D 作⊙O 的切线交BC 于点E ，连接OE .(1)求证：△DBE 是等腰三角形；(2)求证：CA ·CE ＝CO ·CB .第15题图16. (2019凉山州)如图，点D 是以AB 为直径的⊙O 上一点，过点B 作⊙O 的切线，交AD 的延长线于点C ，E 是BC 的中点，连接DE 并延长与AB 的延长线交于点F .(1)求证：DF 是⊙O 的切线； (2)若OB ＝BF ，EF ＝4，求AD 的长．第16题图17. 如图，在Rt △ACB 中，∠C ＝90°，D 是AB 上一点，以BD 为直径的⊙O 切AC 于点E ，交BC 于点F ，连接DF .(1)求证：DF ＝2CE ；(2)若BC ＝3，sin B ＝45，求线段BF 的长．第17题图18. (2019新疆)如图，AB是⊙O的直径，CD与⊙O相切于点C，与AB的延长线交于点D, CE⊥AB于点E.(1)求证：∠BCE＝∠BCD；(2)若AD＝10，CE＝2BE，求⊙O的半径．第18题图参考答案第25课时 与圆有关的位置关系点对点·课时内考点巩固1. C 【解析】根据切线的定义进行判断，过圆外一点可以作两条直线和圆相切．2. B 【解析】∵AC 是⊙O 的切线，∴AB ⊥AC ，∵∠C ＝40°，∴∠B ＝50°. 点对线·板块内考点衔接1. D 【解析】如解图，连接OA 、OB ，∵P A 、PB 分别与⊙O 相切于A 、B 两点，∴OA ⊥P A ，OB ⊥PB ，∴∠OAP ＝∠OBP ＝90°，∴∠AOB ＝180°－∠P ＝180°－50°＝130°，∴∠ACB ＝12∠AOB ＝12×130°＝65°.第1题解图2. B 【解析】如解图，连接OA ，∵∠AOC 与∠ABC 是AC ︵所对的圆心角和圆周角，∴∠AOC ＝2∠ABC ＝60°，∵AP 是⊙O 的切线，∴OA ⊥AP ，∴AP ＝OA ·tan ∠AOC ＝1·tan60°＝ 3.第2题解图3. A 【解析】如解图，连接BC ，∵AP 是⊙O 的切线，∴∠BAP ＝90°.∵∠P ＝30°，∴∠AOP ＝60°.∴∠BOC ＝60°.∵OC ＝OA ，∴∠ACP ＝∠BAC ＝12∠BOC ＝30°.∵AB 是⊙O 的直径，∴∠ACB ＝90°.在Rt △ABC 中，∵∠BAC ＝30°，AB ＝10，∴AC ＝5 3.第3题解图4. A 【解析】如解图，设BP 与⊙O 交于点M ，连接OC ，CM .∵PC 是⊙O 的切线，∴∠OCP ＝90°.∵四边形ABMC 是圆内接四边形，∠A ＝119°，∴∠BMC ＝180°－119°＝61°.∵OC ＝OM ，∴∠OCM ＝∠OMC ＝61°.∴在△COM 中，∠COM ＝58°.∴在△COP 中，∠P ＝180°－∠COM －∠OCP ＝180°－58°－90°＝32°.第4题解图5. A 【解析】如解图，连接OA ，过点O 作OD ⊥AB 于点D ，∵⊙O 是等边三角形ABC 的内切圆，∴OD ⊥AB ，D 为AB 的中点．∵AB ＝23，∴AD ＝12AB ＝ 3.∵在等边△ABC 中，∠CAB ＝60°，∴∠OAD＝30°. ∴tan ∠OAD ＝ODAD. ∴ OD ＝AD ·tan30°＝1.第5题解图6. A 【解析】∵AD 是⊙O 的切线，∴OD ⊥AD .在Rt △AOD 中，AD ＝3OD ，∴tan A ＝OD AD ＝OD3OD ＝33.∴∠A ＝30°.∴∠AOD ＝60°.∵OD ＝OB ，∴∠ODB ＝∠ABD ＝12∠AOD ＝30°.∵BD 平分∠ABC ，∴∠CBD ＝∠ABD ＝30°，∴∠ABC ＝60°，∴∠C ＝90°. 在Rt △ABC 中，sin A ＝BC AB ，AB ＝12，∴BC ＝AB ·sin A ＝12×12＝6. 在Rt △CBD 中，CD ＝BC ·tan ∠CBD ＝6×33＝2 3. 7. B 【解析】如解图，连接OD ，∵直线CD 与⊙O 相切于点D ，∴OD ⊥CD ，∴∠ODC ＝90°，∵CD ＝BD ＝43，∴∠C ＝∠B ，∵OD ＝OB ，∴∠B ＝∠ODB ，∴∠DOE ＝∠B ＋∠ODB ＝2∠B ＝2∠C ，在Rt △OCD 中，∠DOE ＝2∠C ，则∠DOE ＝60°，∠C ＝30°，∴OD ＝CD ·tan C ＝43×33＝4，∵DF ⊥AB ，∴∠DEO ＝90°，在Rt △ODE 中，OE ＝OD ·cos ∠EOD ＝4×12＝2.第7题解图8. 45 【解析】∵AB 为⊙O 的直径，∴∠ADB ＝90°，∵BC 为⊙O 的切线，∴AB ⊥BC ，∴∠ABC ＝90°，∵AD ＝CD ，∴△ABC 为等腰直角三角形，∴∠C ＝45°.9. 219 【解析】如解图，连接AB ，∵P A 、PB 是⊙O 的切线，∴P A ＝PB ，∵∠P ＝102°，∴∠P AB ＝∠PBA ＝12(180°－102°)＝39°，∵∠DAB ＋∠C ＝180°，∴∠P AD ＋∠C ＝∠P AB ＋∠DAB ＋∠C ＝180°＋39°＝219°.第9题解图10. 23 【解析】如解图，连接OQ ，则PQ ＝OP 2－OQ 2，根据题意可知OQ 长为定值，若使得PQ 最小，只要OP 最小即可，当OP ⊥AB 时能取得最小值．∵OA ＝OB ＝42，∴AB ＝8，∴OP ＝4，∴PQ ＝42－22＝2 3.第10题解图11. (1)证明：如解图，连接OD ， ∵BC 是⊙O 的切线， ∴OD ⊥BC ， 又∵AC ⊥BC ， ∴OD ∥AC ， ∴∠2＝∠3； ∵OA ＝OD ， ∴∠1＝∠3， ∴∠1＝∠2， ∴AD 平分∠BAC ；第11题解图(2)解：设⊙O的半径为r，在Rt△BOD中，有OD2＋BD2＝OB2，即r2＋42＝(2＋r)2，解得r＝3.∴⊙O的半径为3.12.证明：(1)∵MP与⊙O相切于点M，∴OM⊥MP，又∵AC∥MP，∴OM⊥AC，又∵AB是⊙O的直径，∴∠ACB＝90°，∴BC⊥AC，∴OM∥BC；(2)∵AC∥MP，∠P＝30°，∴∠BAC＝∠P＝30°，∵∠ACB＝90°，∴AB＝2BC，又∵AB＝2OB，∴BC＝OB＝OM，∵OM∥BC，∴四边形BCMO为平行四边形，又∵OB＝OM，∴四边形BCMO为菱形．13. (1)证明：如解图，连接AE.∵AB＝AC，∴△ABC是等腰三角形．∵AB是⊙O的直径，∴∠AEB＝90°，即AE⊥BC，∴E为BC边的中点，∴BE＝CE；第13题解图(2)解：如解图，连接BD ，设⊙O 的半径为r . ∵BF 为⊙O 的切线， ∴∠ABF ＝90°.在Rt △ABF 中，AB 2＋BF 2＝AF 2， 即(2r )2＋42＝(2r ＋2)2， 解得r ＝32.∴AB ＝AC ＝2r ＝3，AF ＝2r ＋2＝5. ∵AB 是⊙O 的直径， ∴∠ADB ＝∠ABF ＝90°. 又∵∠BAD ＝∠F AB ， ∴Rt △ABD ∽Rt △AFB . ∴AB AF ＝AD AB ，即35＝AD3. ∴AD ＝95.14. (1)证明：如解图，连接OE ， ∵OA ＝OE ， ∴∠A ＝∠OEA ，∵∠ACB ＝90°，点D 是AB 的中点， ∴AD ＝CD ， ∴∠A ＝∠DCA ， ∴∠OEA ＝∠DCA ， ∴OE ∥CD ， ∵EF 为⊙O 的切线， ∴OE ⊥EF ， ∴EF ⊥CD ；第14题解图(2)解：∵cos A ＝56，∴AC AB ＝56， ∵AC ＝10， ∴AB ＝12，∵∠ACB ＝90°，点D 是AB 的中点， ∴AD ＝DC ＝12AB ＝6，由(1)可得，OE ∥CD ，∴AE ＝12AC ，△OEA ∽△DCA ，∴AO AD ＝AE AC ＝12， ∴AE ＝EC ＝12AC ＝5，∵cos A ＝cos ∠DCA ＝CFCE ，∴CF ＝256，∴DF ＝CD －CF ＝6－256＝116.15. 证明：(1)如解图，连接OD 、CD ， ∵DE 是⊙O 的切线， ∴∠ODE ＝90°，在Rt △OCE 和Rt △ODE 中，⎩⎪⎨⎪⎧OC ＝OD OE ＝OE ， ∴Rt △OCE ≌Rt △ODE (HL)， ∴DE ＝CE ， ∴∠ECD ＝∠CDE ， ∵AC 是⊙O 的直径， ∴∠CDA ＝90°， ∴∠CDB ＝90°，∴∠B ＋∠ECD ＝90°，∠CDE ＋∠BDE ＝90°， ∵∠ECD ＝∠CDE ， ∴∠BDE ＝∠B ， ∴BE ＝DE ，∴△DBE 是等腰三角形；第15题解图(2)由(1)可得，BE ＝DE ＝CE ， ∴点E 是BC 的中点， ∴OE 是△ABC 的中位线， ∴OE ∥AB ， ∴△COE ∽△CAB . ∴CO CA ＝CE CB， ∴CA ·CE ＝CO ·CB .16. (1)证明：如解图，连接OD ，BD ， ∵BC 是⊙O 的切线， ∴BC ⊥OB ， ∴∠OBC ＝90°. ∵AB 为⊙O 的直径， ∴∠ADB ＝90°. ∴∠CDB ＝90°. ∵E 是BC 的中点， ∴ED ＝EB ＝12BC ，∴∠EDB ＝∠EBD . ∵OD ＝OB ， ∴∠ODB ＝∠OBD ， ∴∠ODF ＝∠OBC ＝90°， ∴DF ⊥OD .∵OD 是⊙O 的半径， ∴DF 是⊙O 的切线；第16题解图(2)解：由(1)知∠ODF ＝90°，∵OD ＝OB ＝BF ， ∴sin F ＝OD OF ＝12，∴∠F ＝30°，∵∠DOB ＋∠F ＝90°， ∴∠DOB ＝60°， ∴△ODB 是等边三角形， ∴∠OBD ＝60°， ∴tan ∠OBD ＝ADBD ＝3，∴AD ＝3BD . ∵BC ⊥AF ， ∴BE EF ＝sin F ＝12. ∵EF ＝4， ∴BE ＝2，∴BF ＝EF 2－BE 2＝23＝OB ＝DB ， ∴AD ＝3BD ＝6.17. (1)证明：如解图，连接OE 交DF 于点G ， ∵AC 切⊙O 于点E ， ∴∠CEO ＝90°， 又∵BD 为⊙O 的直径， ∴∠DFC ＝∠DFB ＝90°， ∵∠C ＝90°，∴四边形CEGF 为矩形， ∴CE ＝GF ，∠EGF ＝90°， ∴DF ＝2CE ；第17题解图(2)解：在Rt △ABC 中，∵∠C ＝90°，BC ＝3，sin B ＝45，∴AB ＝5，设OE ＝x ，∵OE ∥BC ， ∴△AOE ∽△ABC ，∴OE BC ＝AO AB， ∴x 3＝5－x 5， ∴x ＝158，∴BD ＝2OE ＝154，在Rt △BDF 中，∵∠DFB ＝90°，sin B ＝45，∴cos B ＝35＝BF BD ＝BF154，∴BF ＝94.18. (1)证明：如解图，连接OC ，AC ， ∵AB 是⊙O 的直径， ∴∠ACB ＝90°，∴∠ACO ＋∠OCB ＝90°， 又∵CD 是⊙O 的切线， ∴∠OCD ＝90°， ∴∠OCB ＋∠BCD ＝90°. ∴∠ACO ＝∠BCD . ∵CE ⊥AB ， ∴∠CEB ＝90°， ∴∠BCE ＋∠ABC ＝90°. ∵∠A ＋∠ABC ＝90°， ∴∠BCE ＝∠A . ∵OA ＝OC ，∴∠A ＝∠ACO ＝∠BCD . ∴∠BCE ＝∠BCD ；第18题解图(2)解：如解图，过点B 作BF ⊥CD 于点F ，得△BFD ∽△CED . 由(1)得∵BC 平分∠ECD ，∴BF ＝BE . ∵CE ＝2BE ， ∴BD CD ＝BF CE ＝BE CE ＝12. 即CD ＝2BD .∵∠BCD ＝∠A ，∠CDB ＝∠ADC ， ∴△CBD ∽△ACD ， ∴BD CD ＝CD AD. ∵AD ＝10， ∴BD ＝52，∴AB ＝152，∴OA ＝154.∴⊙O 的半径为154.第六单元 圆第26课时 与圆有关的计算点对点·课时内考点巩固5分钟1. (2019长沙)一个扇形的半径为6，圆心角为120°，则这个扇形的面积是( ) A. 2π B. 4π C. 12π D. 24π2. (2019青海)如图，在扇形AOB 中，AC 为弦，∠AOB ＝140°，∠CAO ＝60°，OA ＝6，则BC ︵的长为( )第2题图A. 4π3 B. 8π3C. 23πD. 2π3. (2019哈尔滨)一个扇形的弧长是11π cm ，半径是18 cm ，则此扇形的圆心角是________度．点对线·板块内考点衔接15分钟1. (2019枣庄)如图，在边长为4的正方形ABCD 中，以点B 为圆心，AB 为半径画弧，交对角线BD 于点E ，则图中阴影部分的面积是(结果保留π)( )A. 8－πB. 16－2πC. 8－2πD. 8－12π第1题图2. (2019绍兴)如图，△ABC 内接于⊙O ，∠B ＝65°，∠C ＝70°.若BC ＝22，则BC ︵的长为( ) A. π B. 2π C. 2π D. 22π第2题图3. (2019青岛)如图，线段AB 经过⊙O 的圆心，AC ，BD 分别与⊙O 相切于点C ，D .若AC ＝BD ＝4，∠A ＝45°，则CD ︵的长度为( )A. πB. 2πC. 22πD. 4π第3题图4. (2019南充)如图，在半径为6的⊙O 中，点A ，B ，C 都在⊙O 上，四边形OABC 是平行四边形，则图中阴影部分的面积为( )A. 6πB. 33πC. 23πD. 2π第4题图5. (2019山西)如图，在Rt △ABC 中，∠ABC ＝90°，AB ＝23，BC ＝2，以AB 的中点O 为圆心，OA 的长为半径作半圆交AC 于点D ，则图中阴影部分的面积为( )A.534－π2 B. 534＋π2C. 23－πD. 43－π2第5题图6. (2019泰安)如图，将⊙O 沿弦AB 折叠，AB ︵恰好经过圆心O ，若⊙O 的半径为3，则AB ︵的长为( ) A. 12π B. π C. 2π D. 3π第6题图7. (2019重庆A 卷)如图，在菱形ABCD 中，对角线AC ，BD 交于点O ，∠ABC ＝60°，AB ＝2.分别以点A ，点C 为圆心，以AO 的长为半径画弧分别与菱形的边相交，则图中阴影部分的面积为________．(结果保留π)第7题图8. (全国视野创新题推荐·2019贵阳)如图，用等分圆的方法，在半径为OA 的圆中，画出了如图所示的四叶幸运草，若OA ＝2，则四叶幸运草的周长是________．第8题图点对面·跨板块考点迁移2分钟1. (2019天水)如图，在平面直角坐标系中，已知⊙D 经过原点O ，与x 轴、y 轴分别交于A 、B 两点，B 点坐标为(0，23)，OC 与⊙D 相交于点C ，∠OCA ＝30°，则图中阴影部分的面积为________．(结果保留根号和π)第1题图参考答案第26课时 与圆有关的计算点对点·课时内考点巩固1. C 【解析】∵扇形的半径为6，圆心角为120°，∴S 扇形＝120·π·62360＝12π.2. B 【解析】如解图，连接CO ，∵OC ＝OA ，∠CAO ＝60°，∴△AOC 为等边三角形．∴∠AOC ＝60°，∴∠BOC ＝∠AOB －∠AOC ＝80°，∴BC ︵的长为80×6π180＝8π3.第2题解图3. 110 【解析】设此扇形的圆心角为n °，根据题意得l ＝nπr 180＝nπ·18180＝11π，解得n ＝110. 点对线·板块内考点衔接1. C 【解析】∵正方形ABCD 的边长为4，∴AB ＝4，∠ABD ＝45°.∴S 阴影＝S △ABD －S 扇形ABE ＝12×AB 2－45π×AB 2360＝12×42－45π×42360＝8－2π.2. A 【解析】如解图，连接OB ，OC .∵∠ABC ＝65°，∠ACB ＝70°，∴∠A ＝180°－∠ABC －∠ACB ＝45°，∵∠1＝2∠A ＝90°，OB ＝OC ，∴△OBC 是等腰直角三角形，∵BC ＝22，∴OB ＝OC ＝2，∴BC ︵的长为90×π×2180＝π.第2题解图3. B 【解析】如解图，连接OC ，OD .∵AC ，BD 分别与⊙O 相切于点C ，D ，∴OC ⊥AC ，OD ⊥BD . ∵∠A ＝45°，∴△ACO 是等腰直角三角形，∴AC ＝OC ＝OD ＝4.∵AC ＝BD ＝4，∴△BDO 是等腰直角三角形，∴∠AOC ＝∠BOD ＝45°，∴∠COD ＝90°. ∴CD ︵的长为90π×4180＝2π.第3题解图4. A 【解析】如解图，连接OB ，交AC 于点D .由题意易知四边形OABC 为菱形，∴△OAB 为等边三角形，∴S △OAD ＝S △BCD ，∠AOB ＝60°，∵⊙O 的半径为6.∴S 阴影＝S 扇形AOB ＝60360×π×62＝6π.第4题解图5. A 【解析】如解图，连接OD ，过点D 作DE ⊥AB 于点E .∵在Rt △ABC 中，AB ＝23，BC ＝2，∴S △ABC ＝12AB ·BC ＝2 3.在Rt △ABC 中，∵tan ∠BAC ＝BC AB ＝223＝33，∴∠BAC ＝30°，∴∠BOD ＝60°.∵OA ＝OB ＝OD ＝12AB ＝3，∴S 扇形BOD ＝60·π·OD 2360＝π2.∵DE ＝OD ·sin60°＝32，∴S △AOD ＝12OA ·DE ＝334.∴S 阴影＝S △ABC －S △AOD －S 扇形BOD ＝534－π2.第5题解图6. C 【解析】如解图，过点O 作OM ⊥AB 于点M ，连接AO 、BO ，∵⊙O 的半径为3，∴OM ＝12×3＝32.∵在Rt △AOM 中，OM ＝12OA ，∴∠OAB ＝30°，∵OA ＝OB ，∴∠OBA ＝∠OAB ＝30°，∴∠AOB ＝120°.∴AB ︵的长为120π×3180＝2π.第6题解图7. 23－2π3 【解析】∵四边形ABCD 是菱形，∴AC ⊥BD ，AO ＝CO ，∵∠ABC ＝60°，∴∠BAD ＝∠BCD ＝120°，∵AB ＝2，∴AO ＝1，BO ＝3，∴S 菱形ABCD ＝12AC ·BD ＝2AO ·BO ＝23，S 扇形＝2×120π×12360＝2π3，∴S 阴影＝23－2π3. 8. 42π 【解析】如解图，根据题意可知四叶幸运草的周长是以AB 为直径的4个半圆弧长，∵OA ＝OB ＝2，∠AOB ＝90°，在Rt △AOB 中，AB ＝OA 2＋OB 2＝22＋22＝22，∴AB ︵的长为12×π×22＝2π，∵四叶幸运草的周长为2π×4＝42π.第8题解图点对面·跨板块考点迁移1. 2π－23 【解析】如解图，连接OD 、AB ，∵∠AOB ＝90°，A 、O 、B 在⊙D 上，∴AB 是⊙D 的直径，∵∠OCA ＝30°，∴∠ODA ＝60°，∠ABO ＝30°.∴△AOD 为等边三角形，∴OD ＝OA ＝OB ·tan30°＝23×33＝2.∴S 阴影＝12S ⊙D －S △AOB ＝12π×22－12×2×23＝2π－2 3.第1题解图。

课时训练(二十七)与圆有关的计算|夯 实 基 础|一、选择题1．[2017·天门]一个扇形的弧长是10π cm 、面积是60π cm 2、则此扇形的圆心角的度数是( ) A ．300° B ．150° C ．120° D ．75°2．120°的圆心角所对的弧长是6π、则此弧所在圆的半径是( ) A ．3 B ．4 C ．9 D ．183．若圆内接正三角形的边心距为1、则这个三角形的面积为( ) A ．2 3 B ．3 3 C ．4 3 D ．6 34．[2016·长春]如图K27－1、PA 、PB 是⊙O 的切线、切点分别为A 、B 、若OA ＝2、∠P ＝60°、则AB ︵的长为( )A.23π B ．π C.43π D.53πK27－1K27－25．[2017·湘潭]如图K27－2、在半径为4的⊙O 中、CD 是直径、AB 是弦、且CD⊥AB、垂足为点E 、∠AOB ＝90°、则阴影部分的面积是( )A ．4π－4B ．2π－4C ．4πD ．2π图K27－36．2015·日照如图K27－3、在等腰直角三角形ABC 中、AB ＝AC ＝8、以AB 为直径的半圆O 交斜边BC 于点D 、则阴影部分的面积为(结果保留π)( )A ．24－4πB ．32－4πC ．32－8πD ．16二、填空题7．[2017·温州]已知扇形的面积为3π、圆心角为120°、则它的半径为________．8．[2017·酒泉]如图K27－4、在△ABC 中、∠ACB ＝90°、AC ＝1、AB ＝2、以点A 为圆心、AC 的长为半径画弧、交AB 边于点D 、则CD ︵的长等于________．(结果保留π)K27－4K27－59．[2017·安徽]如图K27－5、已知等边△ABC 的边长为6、以AB 为直径的⊙O 与边AC 、BC 分别交于D 、E 两点、则劣弧DE ︵的长为________．图K27－610．[2017·岳阳]我国魏晋时期的数学家刘徽创立了“割圆术”、认为圆内接正多边形边数无限增加时、周长就越接近圆周长、由此求得了圆周率π的近似值．设半径为r 的圆内接正n 边形的周长为L 、圆的直径为d.如图K27－6所示、当n ＝6时、π≈L d ＝6r 2r ＝3、那么当n ＝12时、π≈Ld ＝________．(结果精确到0.01、参考数据：sin15°＝cos75°≈0.259)三、解答题11．[2017·郴州]如图K27－7、AB 是⊙O 的弦、BC 切⊙O 于点B 、AD ⊥BC 、垂足为D 、OA 是⊙O 的半径、且OA ＝3.(1)求证：AB 平分∠OAD；(2)若点E 是优弧AEB ︵上一点、且∠AEB＝60°、求扇形OAB 的面积．(计算结果保留π)图K27－712．[2017·长沙]如图K27－8、AB 与⊙O 相切于点C 、OA 、OB 分别交⊙O 于点D 、E 、CD ︵＝CE ︵. (1)求证：OA ＝OB ；(2)已知AB ＝4 3、OA ＝4、求阴影部分的面积．图K27－813．[2016·盐城]如图K27－9、在四边形ABCD 中、AD ∥BC 、AD ＝2、AB ＝2 2.以点A 为圆心、AD 为半径的圆与BC 相切于点E 、交AB 于点F.(1)求∠ABE 的大小及DEF ︵的长度；(2)在BE 的延长线上取一点G 、使得DEF ︵上的一个动点P 到点G 的最短距离为2 2－2、求BG 的长．图K27－9|拓 展 提 升|图K27－1014．[2015·天水]如图K27－10、△ABC 是等边三角形、曲线CDEF 叫作等边三角形的渐开线、其中CD ︵、DE ︵、EF ︵的圆心依次是点A 、B 、C 、如果AB ＝1、那么曲线CDEF 的长是________．15．[2017·盐城]如图K27－11、△ABC 是一块直角三角板、且∠C＝90°、∠A ＝30°、现将圆心为点O 的圆形纸片放置在三角板内部．(1)如图①、当圆形纸片与两直角边AC 、BC 都相切时、试用直尺与圆规作出射线CO ；(不写作法与证明、保留作图痕迹)(2)如图②、将圆形纸片沿着三角板的内部边缘滚动1周、回到起点位置时停止．若BC ＝9、圆形纸片的半径为2、求圆心O 运动的路径长．图K27－11 参考答案1．B [解析] 根据S 扇形＝12l 弧长r 、求得半径r ＝12、由弧长公式l ＝n πr 180、得10π＝n π·12180、解得n ＝150.2．C [解析] 根据弧长公式、得6π＝120πr180、解得r ＝9.3．B [解析] 如图、过点A 作AD⊥BC 于点D O 、∠ODB ＝90°、OD ＝1.∵△ABC 是等边三角形、∴BD ＝CD 、∠OBD ＝12∠ABC＝30°、∴OA ＝OB ＝2OD ＝2、∴AD ＝3、BD ＝3、∴BC ＝2 3、∴△ABC 的面积＝12BC·AD＝12×2 3×3＝3 3.4．C5．D [解析] ∵CD⊥AB、∠AOB ＝90°、∴∠AOC ＝∠BOC＝45°、∴S 阴影＝S 扇形AOC ＝n πr 2360＝45π42360＝2π、故选D.6．A [解析] 如图、连接AD 、OD.∵三角形ABC 是等腰直角三角形、 ∴∠ABD ＝45°.∵AB 是圆的直径、 ∴∠ADB ＝90°、∴△ABD 也是等腰直角三角形、 ∴AD ︵＝BD ︵.∵AB ＝8、∴AD ＝BD ＝4 2、∴S 阴影＝S △ABC －S △ABD －S 弓形AD ＝S △ABC －S △ABD －(S 扇形OAD －12S △ABD )＝12×8×8－12×4 2×4 2－90π×42360＋12×12×4 2×4 2＝16－4π＋8＝24－4π.7．3 [解析] 设扇形的半径为r 、由扇形的面积公式S ＝120πr2360＝3π、得r ＝3.8.π3 [解析] 在Rt △ABC 中、AC ＝1、AB ＝2、∴cosA ＝AC AB ＝12、∴∠A ＝60°、∴CD ︵的长为60π×1180＝π3.9．π [解析] 如图、连接OD 、OE 、易证△ODE 是等边三角形、∠DOE ＝60°、又OD ＝12AB ＝3、根据弧长公式知劣弧DE ︵的长为60·π·3180＝π.10．3.11 [解析] 如图所示、∠AOB ＝30°、∠AOC ＝15°.在直角三角形AOC 中、sin15°＝AC AO ＝ACr＝0.259、所以AC ＝0.259r 、AB ＝2AC ＝0.518r 、L ＝12AB ＝6.216r 、所以π≈L d ＝6.216r2r＝3.108≈3.11.11．解：(1)证明：如图、连接OB 、 ∵BC 切⊙O 于点B 、∴OB ⊥BC 、∵AD ⊥BC 、∴AD ∥OB 、 ∴∠DAB ＝∠OBA、 ∵OA ＝OB 、∴∠OAB ＝∠OBA、 ∴∠DAB ＝∠OAB、 ∴AB 平分∠OAD.(2)点E 在弧AEB ︵上、且∠AEB＝60°、 ∴∠AOB ＝120°、∴S 扇形OAB ＝120360·π·AO 2＝13×π×32＝3π.12．解：(1)证明：连接OC 、∵AB 与⊙O 相切于点C 、∴∠ACO ＝90°、∠BCO ＝90°、 ∵CD ︵＝CE ︵、∴∠AOC ＝∠BOC、 ∴∠A ＝∠B、∴OA ＝OB.(2)由(1)可知△OAB 是等腰三角形、∴BC ＝12AB ＝2 3、∴sin ∠COB ＝BC OB ＝32、∴∠COB ＝60°、∴∠B ＝30°、∴OC ＝12OB ＝2、∴扇形OCE 的面积为：60π×4360＝2π3、△OCB 的面积为：12×2 3×2＝2 3、∴S 阴影＝2 3－2π3.13．解：(1)连接AE 、∵圆与BC 相切于点E 、 ∴AE ⊥BC 且AE ＝2. 又∵AB＝2 2、∴BE ＝2、∠ABE ＝45°. 又∵AD∥BC、 ∴∠BAD ＝135°、 ∴DEF ︵的长度为32π.(2)连接AG 、交DEF ︵于点P 、取DEF ︵上异于点P 的另一点P 1、连接P 1A 、P 1G. 在△P 1AG 中、P 1A ＋P 1G ＞AG 、 又AG ＝AP ＋PG 、∴P 1G ＞PG 、 ∴点P 到点G 的距离最短． 又PG ＝2 2－2、AP ＝2、∴AG ＝2 2、∴∠EGA ＝45°、∴EG ＝2、 又∵BE＝2、∴BG ＝4.14．4π [解析] CD ︵的长是120π×1180＝2π3、DE ︵的长是120π×2180＝4π3、EF ︵的长是120π×3180＝2π、则曲线CDEF 的长是2π3＋4π3＋2π＝4π.15．解：(1)如图①、CP 就是所要求作的射线．(2)如图②、△OO 1O 2就是圆心O 的运动路径． 由题意得OO 1∥BC 、O 1O 2∥AB 、OO 2∥AC. 易证△OO 1O 2∽△CBA. ∴△OO 1O 2的周长△ABC的周长＝OO 1BC. 过点O 作OD⊥B C 、垂足为点D 、过点O 1作O 1E ⊥BC 、O 1F ⊥AB 、垂足分别为点E 、F 、连接BO 1、则四边形ODEO 1是矩形．∵O 1E ＝O 1F 、O 1E ⊥BC 1F ⊥AB 、 ∴BO 1平分∠ABC.∴∠O 1BE ＝12∠ABC＝12×60°＝30°.∴BE ＝3O 1E ＝2 3.∴DE ＝BC －CD －BE ＝9－2－2 3＝7－2 3. ∴OO 1＝DE ＝7－2 3.在Rt △ABC 中、∵BC ＝9、∠A ＝30°、 ∴AB ＝2BC ＝18、AC ＝3BC ＝9 3. ∴△ABC 的周长为27＋9 3. ∴△OO 1O 2的周长27＋9 3＝7－2 39.∴△OO 1O 2的周长为15＋3、即圆心O 的运动路径长为15＋ 3.。

例题
1：圆的性质应用
例 1 如图，CD 是⊙O 的直径，BE 是⊙O 的弦，DC、EB 的延长线相交于点 A．若∠A＝25°， AB＝OC，求∠EOD 的度数．
2：利用圆的性质进行证明
例1如图，⊙O 的半径OA、OB 分别交弦C D 于点E、F，且CE＝DF．试说明∠OEF 与∠OFE 的关系．
例 2 如图，O为AB所在圆的圆心，已知OA⊥OB，M为弦AB的中点，且MC∥OB交AB于点C．求AC的度数．60
延长CM交OA于E,OE=1/2 OA=1/2 OC
3：圆的性质和矩形性质综合
例 1 如图，点 A、D、G、M 在半圆 O 上，四边形 ABOC、DEOF、HMNO 为矩形，设 BC＝a，EF＝b，NH＝c．则下列各式正确的是( )
A．a>b>c B．a＝b＝c C．c>a>b D．b>c>a
4：点与圆的位置关系中分类讨论思想
例1若⊙O 所在平面上的一点P到⊙O 上的点的最大距离是10，最小距离是2，则此圆的半径为
5：利用圆的定义与直角三角形的性质综合进行证明
例1、已知：如图，BD、CE 是△ABC 的高，M 为B C 的中点，试说明点B、C、D、E 在以点M为圆心的同一个圆上．
例2、如图，在□ABCD 中，∠BAD 为钝角，且A E⊥BC，AF⊥CD． (1)求证：A、E、C、F 四点共圆；
(2)设线段B D 与(1)中的圆交于点M、N．求证：BM＝ND．。

课时训练(二十七) 圆的有关概念与性质|夯实基础|1.☉O的半径为5cm,点A到圆心O的距离OA=3cm,则点A与☉O的位置关系为()A.点A在☉O上B.点A在☉O内C.点A在☉O外D.无法确定2.[2016·黄石] 如图27-9所示,☉O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON的长为()图27-9A.5B.7C.9D.113.如图27-10,已知半径OD与弦AB互相垂直,垂足为C.若AB=8cm,CD=3cm,则☉O的半径为()图27-10A.cmB.5cmC.4cmD.cm4.如图27-11,已知☉O的直径AB⊥CD于点E,连接OC,OD,则下列结论不一定正确的是()图27-11A.CE=DEB.AE=OEC.=D.△OCE≌△ODE5.[2018·聊城] 如图27-12,在☉O中,弦BC与半径OA相交于点D,连接AB,OC.若∠A=60°,∠ADC=85°,则∠C的度数是()图27-12A.25°B.27.5°C.30°D.35°6.[2018·南充] 如图27-13,BC是☉O的直径,A是☉O上的一点,∠OAC=32°,则∠B的度数是()图27-13A.58°B.60°C.64°D.68°7.[2018·济宁] 如图27-14,点B,C,D在☉O上,若∠BCD=130°,则∠BOD的度数是()图27-14A.50°B.60°C.80°D.100°。

课时训练(二十七)圆的有关性质(限时:30分钟)|夯实基础|1.下列四个命题:①直径所对的圆周角是直角;②圆既是轴对称图形,又是中心对称图形;③在同圆中,相等的圆周角所对的弦相等;④三点确定一个圆.其中正确命题的个数为()A.1B.2C.3D.42.若☉O的半径是5,点A到圆心O的距离是7,则点A与☉O的位置关系是()A.点A在☉O上B.点A在☉O内C.点A在☉O外D.点A与圆心O重合3.[2017·永州]小红不小心把家里的一块圆形玻璃镜打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图K27-1所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是()图K27-1A.AB,AC边上的中线的交点B.AB,AC边上的垂直平分线的交点C.AB,AC边上的高所在直线的交点D.∠BAC与∠ABC的角平分线的交点4.[2018·聊城]如图K27-2,☉O中,弦BC与半径OA相交于点D,连接AB,OC.若∠A=60°,∠ADC=85°,则∠C的度数是()图K27-2A.25°B.27.5°C.30°D.35°5.[2018·邵阳]如图K27-3所示,四边形ABCD为☉O的内接四边形,∠BCD=120°,则∠BOD的大小是 ()图K27-3A.80°B.120°C.100°D.90°6.[2018·枣庄]如图K27-4,AB是☉O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为()图K27-4A.B.2C.2D.87.[2017·大连]如图K27-5,在☉O中,弦AB=8 cm,OC⊥AB,垂足为C,OC=3 cm,则☉O的半径为cm.图K27-58.如图K27-6,已知AB是☉O的弦,半径OC垂直于AB,点D是☉O上一点,且点D与点C位于弦AB两侧,连接AD,CD,OB,若∠BOC=68°,则∠ADC= 度.。

课时训练（二十七)圆的基本概念和性质（限时:30分钟）|夯实基础|1。

到三角形三个顶点的距离都相等的点是这个三角形的（)A.三条高的交点B.三条角平分线的交点C。

三条中线的交点D。

三条边的垂直平分线的交点2。

如图K27-1,在半径为5 cm的☉O中，弦AB=6 cm，OC⊥AB于点C,则OC= (）图K27-1A。

3 cm B.4 cm C.5 cm D。

6 cm3.如图K27-2，AB为☉O的直径，点C在☉O上，若∠ACO=50°,则∠B的度数为（)图K27—2A.60° B。

50° C.40° D。

30°4.[2017·苏州］如图K27-3，在Rt△ABC中,∠ACB=90°,∠A=56°.以BC为直径的☉O交AB 于点D,E是☉O上一点,且=，连接OE，过点E作EF⊥OE，交AC的延长线于点F，则∠F的度数为（）图K27-3A。

92° B.108° C.112°D.124°5.如图K27-4所示，点P在以AB为直径的半圆O内，连接AP，BP,并延长分别交半圆于点C,D，连接AD，BC，并延长交于点F,作直线PF,与AB交于点E，下列说法一定正确的是（）图K27-4①AC垂直平分BF；②AC平分∠BAF；③FP⊥AB;④BD⊥AF。

A。

①③ B.①④C。

②④D。

③④6.[2018·无锡]如图K27—5，点A,B，C都在☉O上，OC⊥OB，点A在劣弧上,且OA=AB,则∠ABC= 。

图K27-57.［2018·南通]如图K27—6,AB是☉O的直径,点C是☉O上的一点，若BC=3,AB=5,OD⊥BC 于点D，则OD的长为.图K27-68。

[2018·嘉兴］如图K27—7，量角器的0度刻度线为AB，将一矩形直尺与量角器部分重叠，使直尺一边与量角器相切于点C,直尺另一边交量角器于点A,D，量得AD=10 cm，点D在量角器上的读数为60°,则该直尺的宽度为cm.图K27-79.［2016·扬州]如图K27—8，☉O是△ABC的外接圆，直径AD=4，∠ABC=∠DAC,则AC的长为.图K27-810.[2017·盐城]如图K27—9，将☉O沿弦AB折叠,点C在上,点D在上,若∠ACB=70°,则∠ADB= °.图K27-911.［2017·南京］如图K27—10,四边形ABCD是菱形,☉O经过点A，C,D,与BC相交于点E,连接AC,AE,若∠D=78°，则∠EAC= 。