当前位置：文档之家 › 太阳影子定位-2015高教社杯全国大学生数学建模竞赛题

太阳影子定位-2015高教社杯全国大学生数学建模竞赛题

  • 格式：docx
  • 大小：373.44 KB
  • 文档页数：21

下载文档原格式

  / 21

合集下载

全国大学生数学建模2015年国二a题

全国大学生数学建模2015年国二a题

2015高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。

我们知道，抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。

我们郑重承诺，严格遵守竞赛规则，以保证竞赛的公正、公平性。

如有违反竞赛规则的行为，我们将受到严肃处理。

我们授权全国大学生数学建模竞赛组委会，可将我们的论文以任何形式进行公开展示（包括进行网上公示，在书籍、期刊和其他媒体进行正式或非正式发表等）。

我们参赛选择的题号是（从A/B/C/D中选择一项填写）： A我们的参赛报名号为（如果赛区设置报名号的话）：所属学校（请填写完整的全名）：参赛队员(打印并签名) ：1.2.3.指导教师或指导教师组负责人(打印并签名)：日期：年月日赛区评阅编号（由赛区组委会评阅前进行编号）：编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：全国统一编号（由赛区组委会送交全国前编号）：全国评阅编号（由全国组委会评阅前进行编号）：太阳影子定位摘要本文研究了太阳影子定位问题，基于天球坐标系相关知识、球面几何理论以及相似度理论，对不同情况下的数据，建立了相应的数学模型并得到了最优的匹配地点与日期。

问题1中，利用球面三角形余弦定理给出了太阳高度角公式，并建立了影子长度变化的数学模型，定性的分析了影子长度关于时角、当地纬度以及赤纬角的变化规律：(1). 时角的绝对值越大，影子长度越大；(2). 在同一经度上（即时角一定），当地纬度与此时的太阳赤纬之差越大，影子长度越大；(3). 在同一纬度不同经度上，当地经度和此时太阳直射点所在的经度之差越大，影子长度越大。

用所建的模型，得到了2015年10月22日北京时间9:00-15:00之间天安门广场3米高的直杆的太阳影子长度的变化曲线。

2015数学建模A题论文介绍

2015数学建模A题论文介绍

2015数学建模A题论⽂介绍A题太阳影⼦定位摘要本⽂⾸先确定了不同地点不同⽇期的直杆影长的模型，利⽤该模型解决了不同地点不同⽇期直杆影⼦变化和时间的的关系，为分析视频的拍摄地点和⽇期提供了模型上的基础。

对于问题⼀，为了确⽴直杆的影长与时间的关系，建⽴了地球坐标系和天球坐标系，引⼊太阳⾼度⾓、⾚纬、太阳时⾓、时差等参数变量。

利⽤太阳⾼度⾓和时间的关系建⽴了影长和时间的关系模型。

利⽤MATLAB软件求得影长关于时间的变化曲线，从9点到15点影⼦长度先减⼩后增⼤，在北京时间12点14分直杆影长最短，最短为3.5⽶，在北京时间9点直杆影长最长，长度为7.3⽶。

对于问题⼆，结合问题⼀中各参数变量之间的关系，使⽤Bourges算法和太阳⽅位⾓与时间的关系，得到确定直杆所在地点的数学模型，将附件1所给数据带⼊模型，利⽤excel和MATLAB软件进⾏求参数和拟合函数图像，求得直杆所处的可能地点为北纬19.21，东经108.43。

该地点在海南。

或者为南纬3.9412度，东经137.3度。

该地点在为印度尼西亚纳⽐雷附近。

对于问题三，由所给影⼦顶点坐标数据计算出各时间点的太阳⽅位⾓，利⽤excel 软件拟合出太阳⽅位⾓与时间的关系，进⽽确定直杆点的经度，结合问题⼆的数学模型得到直杆地点和⽇期求法的数学模型。

再次通过MATLAB进⾏求参数和拟合函数图像，求出了附件2地点可能为北纬39.88，东经79.7925或南纬39.88，东经79.7925，可能⽇期为：5⽉25号和7⽉20号或1⽉17号和1⽉26号。

对于问题四，提取出视频所有的帧数，等差得选取其中的20张进⾏模拟，利⽤3DMAX 软件仿真出视频的场景，通过测量所建模型中影⼦长度，确定出20组影⼦顶点坐标数据，再⽤问题⼆中所⽤到的模型进⾏求解，得到经纬度为北纬15.2，东经113.9.拍摄地点在海南省的三沙市。

⽤问题三中的模型求解得到拍摄地点纬度为0，东经123.8度在印度尼西亚，⽇期为3⽉21号或10⽉23号。

2015数学建模国赛论文A题

2015数学建模国赛论文A题

利用影子确定视频拍摄地点和日期的建模和算法摘要本文研究的问题是如何通过分析视频中物体的太阳影子变化，确定视频拍摄的地点和日期。

建模整体思路是，先建立一系列分析用到的物理量，设定一些假设和约束条件，使得问题求解有可行性，之后对这些物理量进行演绎。

建模使用的软件平台主要是matlab ，分析用到的主要参量是太阳赤纬、时角、高度角、方位角、纬度，分析过程当中用到的方法有，建立物理概念，明确物理意义，比如引用天球坐标系的概念，在天球坐标系的基础上进行物理分析，通过对建立的参变量进行物理关系的推导，形成公式体系进行求解，对题目所给予的影子坐标数据进行适当变换处理，使用matlab 进行合理的拟合，对于用公式法和方程法没法顺利解决的问题使用穷举法作为解题的补充，对于视频中坐标的取法用到了坐标转换的思想。

其中主要公式有 1.cos sin sin coshA δω= 2.tanh H L= 3. sinh sin sin cos cosh cos A ϕδϕ-= 4. sinh=cos Ωcos φcos δ+sin φsin δ第一问，通过物理量变换，先求出高度角，进而得到影子长度与时间变化关系。

第二问，拟合点求经度，取点套公式求纬度。

第三问，方程思想，过程复杂，采用穷举法近似实现求解。

第四问，难点在于通过视频分析，得到影子端点的变化坐标，进而将问题转化成第二问，已知日期（太阳赤纬），时间（时角），求解经度纬度。

关键词：天球坐标系 物理量演绎分析 matlab 数据拟合分析 二元方程组近似穷举法 坐标转换思想1.问题重述与分析如何确定视频的拍摄地点和拍摄日期是视频数据分析的重要方面，太阳影子定位技术就是通过分析视频中物体的太阳影子变化，确定视频拍摄的地点和日期的一种方法。

1.建立影子长度变化的数学模型，分析影子长度关于各个参数的变化规律，并应用你们建立的模型画出2015年10月22日北京时间9:00-15:00之间天安门广场（北纬39度54分26秒,东经116度23分29秒）3米高的直杆的太阳影子长度的变化曲线。

2015年数学建模竞赛题目

2015年数学建模竞赛题目

2015年数学建模竞赛题目
2015年数学建模竞赛题目包括：
1. 飞行器设计优化：根据给定的飞行器参数，建立数学模型，并求解最优设计方案。

此题属于优化问题，需要运用线性规划、非线性规划等相关知识。

2. 水质监测与评价：分析给定的水质监测数据，建立评价模型，对水质进行评价。

此题涉及数据处理、统计分析、模糊评价等知识。

3. 智能家居系统：设计一个智能家居系统，满足给定的功能需求。

此题需要了解图论、动态规划等知识，以解决网络拓扑结构、任务调度等问题。

4. 太阳影子定位：建立影子长度变化的数学模型，分析影子长度关于各个参数的变化规律，并应用建立的模型给出若干个可能的地点。

此题涉及太阳高度、地理坐标、时间等因素的分析和建模。

此外，还有2015年题目包括但不限于交通流量、营销策略等主题，具体的主题内容可以根据具体的竞赛背景和要求来确定。

在选择和确定数学建模题目时，应综合考虑自身兴趣、专业知识储备、数据可得性以及问题实际意义等多个方面因素。

2015年数学建模国赛A题

2015年数学建模国赛A题
3
因此对于地球来说太阳的曲率可忽略不计，故可将太阳光看作平行光。在太阳高 度角为 时，物体影长如图 1 所示：
太阳光

l
L
地面
图 1 物体影长及太阳高度角示意图 由图可知，物体高度 L 、直杆影长 l 及太阳高度角 满足三角函数关系，故在太 阳光下直杆的影子长度为 L l tan 太阳高度角 的计算公式为 (1) sin =sin sin +cos cos cos w 其中 表示观测地的地理纬度（北纬为正，南纬为负） ， 表示太阳赤纬角(太阳 直射点纬度） ， w 表示地方时时角，太阳高度角随观测地点地理纬度、地方时时 角及观测日期对应太阳赤纬角的变化而变化。 太阳赤纬角是地球赤道平面与太阳和地球中心的连线之间的夹角， 在地球的 公转运动中，赤纬角在+23 °26′与-23 °26′的范围内移动，其具体值是已知 的且只与 有关，表达式为 0.3723 23.2567sin 0.1149sin 2 0.1712sin 3 (2) 0.758cos 0.3656cos 2 0.0201cos3 式中 称日角，日角满足公式 2 ( N N 0 ) (3) 365.2422 其中 N 表示积日，所谓积日，就是日期在年内的顺序号，例如，1 月 1 日其积日 为 1，平年 12 月 31 日的积日为 365，闰年则为 366，等等。设年份为 T ，则 N 0 可 表示为
表示含义 直杆影子长度 太阳高度角 观测地地理纬度 观测地地理经度 太阳赤纬 积日 地区时角 日角 直杆高度 时间 年份 比例尺
五、 模型建立与求解
在地球上不同地区和不同时间，太阳下物体的影子长度各不相同。根据太阳 影子变化情况，判断物体具体位置和时间在实际生活中有重要意义。通过研究物 体在水平地面上太阳影子随时间变化规律，太阳影子长度与位置、时间的关系， 可根据太阳影子方向及其变化规律了解物体所在的大致位置和时间。 5.1 影子长度变化模型 在不同日期、不同时间，太阳光线照射物体的角度不相同，引起物体影子的 长度和方向随着太阳高度和角度的变化而变化， 因此同一物体在不同时间的太阳 影子长度和方向各不相同。为了建立影子长度变化的模型，根据相关公式，研究 影子长度变化规律。 5.1.1 影长变化模型 物体影子在不同时间的长度和方向均不相同。故假设某物体垂直于水平地 面，高度为 L ，其影子长度为 l 。首先引入太阳高度角，即太阳光的入射方向和 地平面之间的夹角。 太阳半径为 696300 千米， 远大于地球的半径 6371.393 千米，

太阳影子定位-2015年全国数学建模比赛a题全国二等奖论文

太阳影子定位-2015年全国数学建模比赛a题全国二等奖论文

太阳影子定位摘要本文研究的问题是分析直杆在太阳的照射下，影子的角度和长度的变化，再结合相关地理知识和数学几何模型，推算出具体的所在地点和具体日期。

该模型可以用于太阳影子定位技术中，根据物体在阳光照射下影子的变化进行定位。

对于问题一，我们首先根据地球与太阳的位置关系列出太阳赤纬角，太阳高度角，太阳时角的计算式，其中需对较粗略的太阳赤纬角计算式进行修正，得出精准的计算式。

再建立数学几何模型，根据太阳高度角，影长与杆长形成的角边关系，列出影长的计算式。

最后建立一个太阳日照影长模型，该模型以太阳高度角计算式，太阳赤纬角计算式，太阳时角计算式为子函数，以太阳赤纬角，太阳日角，太阳时角，时间初值为中间变量，以当地经纬度，从1月1日到测量日的天数，时间，杆长，年份为自变量的复合函数数学模型。

然后采用由内到外计算法对此复合函数进行求解，计算出从九点到十五点的影长和太阳高度角的变化，得出直杆的太阳影子长度的变化曲线。

对于问题二，我们首先分析因为时间日期已给出，所以根据太阳赤纬角计算式可知太阳赤纬角为已知量，接着我们将影长的计算式进行等式移项变换，得到一个拟合杆长及经纬度的非线性最小二乘模型，该模型将问题一中太阳日照影长模型作为参数拟合对象，以杆长和影长与太阳高度角正切值之积的差值最小误差平方和为目标函数，以太阳高度角计算式，太阳时角计算式为约束条件，以测量时间，天数，影长为已知量。

将该模型在1stopt 软件中运行，采用麦夸尔特算法和通用全局最优化法对该模型进行迭代计算，对实验结果统计分析后得出该直杆相应的北纬为19.29392848度，东经为108.7225248度（海南岛的西海岸）。

对于问题三，除了需要拟合杆长和经纬度以外，还需拟合日期，同样参照影长等式移项变换公式，得到一个拟合杆长、经纬度及日期的非线性最小二乘模型。

同样采用问题二的计算方法得到多组结果，其中附件二最优解地点为新疆维吾尔自治区喀什地区巴楚县(40.0025°N,79.6587°E)，附件三最优解地点为湖北省十堰市郧西县（32.9638°N,110.277°E ）。

2015年全国大学生数学建模竞赛A题

2015年全国大学生数学建模竞赛A题

太阳影子定位技术问题的数学模型摘要本文涉及的是太阳影子定位技术问题。

在已知视频中物体的太阳影子变化的情况下，要确定视频的拍摄地点和拍摄日期。

首先，分析了文中四个问题的关系，发现前三个问题的已知条件逐步减少，问题难度依次递进。

第四问则给出一个实际问题，该问题需要转化成数学模型利用前三问的方法求解；随后，建立了L-G模型、MinZ-模型等，并应用非线性最小二乘法、遗传算法等算法对模型求解。

得到基于模型的合理结果。

最后，将第四问的实际问题转化数学模型并求解，进而解决问题。

对于问题一，要解决的问题是杆长与影子长度的关系，根据天文、几何知识，我们建立了模型来刻画问题给出的参数之间联系，如赤纬角模型、时角模型、太阳高度角模型、影子长度模型（L-G模型）等；分析了各参数对影子长度的影响；最后运用MATLAB绘制出具体给定参数下的3米高直杆的影子变化曲线；从曲线可以看出在9:00到15:00这段时间里，影子长度先变短后变长，最短为3.627米，最长为7.182米。

问题二提供了一个关于时间、影子坐标的附件1，杆长未知，为了确定直杆所处的地点，本问建立了MinZ-模型，首先将经度、纬度、杆长离散化，搜索出大概的可行解，然后运用非线性最小二乘算法，选取matlab中的lsqcurvefit命令，以可行解为初值，再运用非线性最小二乘算法，选取MATLAB中的lsqcurvefit命令，在控制残差在10−8之内范围的情况下得到了三个可能地点皆在海南省昌江县内，最小误差的地点为海南省江黎族自治县，北纬19.3025°，东经108.6988°，此时对应直杆高度为2.0219m。

同时，将结果代入问题一的模型进行检验，验证了模型的稳定性和算法的合理性。

问题三沿用问题一的模型和问题二的算法，由于一个已知量变成一个变量，根据算法特点，在增加一个变量的情况下，算法搜索影长差时只需要增加一重循环。

关于附件2数据，残差最小对应的位置为北纬39.8926°，东经79.7438°，具体地点在新疆维吾尔自治区喀什地区巴楚县。

2015年全国大学生数学建模竞赛A题优秀论文太阳影子定位模型教程

2015年全国大学生数学建模竞赛A题优秀论文太阳影子定位模型教程
5.1. 旗杆影长的求解 5.1.1. 模型建立
我们依据太阳位置算法[2]（ SPA）得到太阳位置的几何模型图如图 1 所示：
图 1 太阳位置的几何模型
图中 为高度角， 为方位角， 为纬度角， 为赤纬角， 为太阳时角， 和 能由下列式子计算得到(公式来源:/1GU1iS)：
（1.2）
其中 为一个参数，能通过如下公式得到
2 (d 1) 365
（1.3）
式中， h 为北京时间， 为当地经度， d 为日期，即 1 月 1 日就用 d 1来表
示，假设一年为 365 天，则 d 365表示 12 月 31 日。由式（1.1）可知，相邻两天的赤
纬角 差值几乎为 0，因此当闰年时，我们设定 2 月 28 日的 d 59 ，29 日时 d 59 ，
g( ) (0.006918 - 0.399912 cos( ) 0.070257 sin( ) - 0.006758 cos(2 ) 0.000907 sin(2 ) - 0.002697 cos(3 ) 0.00148 sin(3 ))
（1.1 ）
h15 300
关键词：太阳位置算法 最小二乘法 遗传算法 太阳影子定位模型
一． 问题重述
1.1. 问题背景 如何确定视频的拍摄地点和拍摄日期是视频数据分析的重要方面，太阳影子定位
技术就是通过分析视频中物体的太阳影子变化来确定视频拍摄的地点和日期的一种方 法。 1.2. 问题提出 1. 建立影子长度变化的数学模型，分析影子长度关于各个参数的变化规律，并应用建
5.1.2. 模型求解
首先根据问题分析和模型，我们将观测日期代入得到赤纬角 21.8985 ，负号表
示太阳直射点在南半球，然后代入求出太阳时角 和高度角 在不同时刻的值，得到表

2015全国大学生数学建模竞赛

2015全国大学生数学建模竞赛

在数据的原始坐标系 c’中相邻两个时刻������������+1和������������的竿影夹角变化记为：
Δ������′(������������ ); 由向量内积关系可以得到：
cos (Δ������′(������������ ))
=
���⃗⃗���⃗���⃗⃗���⃗⃗(⃗���⃗⃗���⃗⃗���⃗���) ∙⃗���⃗���⃗⃗���⃗⃗���⃗(⃗⃗���⃗⃗���⃗⃗���⃗���⃗+⃗⃗⃗1⃗⃗) |���⃗⃗���⃗���⃗⃗���⃗(⃗⃗⃗���⃗⃗���⃗⃗���⃗���) |∙ |⃗���⃗���⃗⃗���⃗⃗���⃗(⃗⃗���⃗⃗���⃗⃗���⃗���⃗+⃗⃗⃗1⃗⃗)
下面确定������ ������������������及������ ������������������ ： 由所给的数据表格可以计算出：当天的第一组数据时，太阳直射点在 10.5N,79.5E;最后一组数据
时，太阳直射点在 10.5N,64.5E; 由于太阳照射不到的地区不可能有竿的阴影，故而目标点的经度区域为 10.5W,154.5E;
对于问题四，本文将视频材料等时间间隔采样（截图），依据针孔相机成像机理及空间坐标变换 理论，将截图中竿顶端的像素坐 标数据转化为大地坐标系中的坐 标数据，继进而通过公式演算得 到 竿影夹角差分的正切比值仅与时刻有关的结论，从而引用网格搜索模型求解对应的经纬度坐标点。
关键词： 网格搜索 多目标最优化 拟合 针孔相机标定
|；p
为竿影的顶点
则由原始数据即可得到Δ������′(������������ )与时刻的关系，也可以得到������′(������������ )与时刻的关系

太阳影子定位问题(数学建模 )

太阳影子定位问题(数学建模 )
针对问题四，我们首先将视频材料以 3 分钟为间隔得到 14 张静态图片，对这些图 片进行灰度处理，然后采用 Otus 最大类间误差法把杆子和影子从背景中分割出来，从 而得到影子实际长度和灰度值坐标的转换关系，最终得到了 8:54-9:33 每隔 3 分钟的影 子长度，再利用问题二模型得出视频的拍摄地点为：内蒙古鄂尔多斯市 （109.45°E,39.65°N，），假设拍摄日期也未知，则利用问题三的模型求解出的拍摄日序 为 203 即 7 月 22 日，与真实时间 7 月 13 日误差较小，说明模型较为精确，得到的结果 较为可靠。
针对问题二，附件 1 给出了 2015 年 4 月 18 日时，某个固定直杆在水平地面上的太 阳影子的顶点坐标数据，但规定的 ������轴方向和������轴方向未知。可将顶点坐标数据转化为 影长������，从而经问题二转化为问题一的逆向求解，由于未知参量较多，先通过引入影长 比������������消除杆高ℎ未知的影响，再采用最小二乘法拟合的方法【2】求解即可。
图 2 直杆投影的几何模型
由图可知，直杆的长度ℎ与其太阳影子������的长度之间有如下关系：
������ = ℎ cot ������ 联系以上各关系式可以得到如下的有关影子长度变化的数学模型：
������ = ℎ cot ������
sin ������ = sin ������������ sin ������ + cos ������������ cos ������ cos ������
2.根据某个固定直杆在水平地面上的太阳影子的顶点坐标数据来建立数学模型，用 以确定其所处的地点。再将附件 1 的影子顶点坐标数据代入该模型，求解出所有可能的 地点。
3.根据某个固定直杆在水平地面上的太阳影子的顶点坐标数据来建立数学模型，用 以确定其所处的地点和日期。将附件 2 和附件 3 的影子顶点坐标数据带入模型，一次 性给出若干个可能的地点与日期。

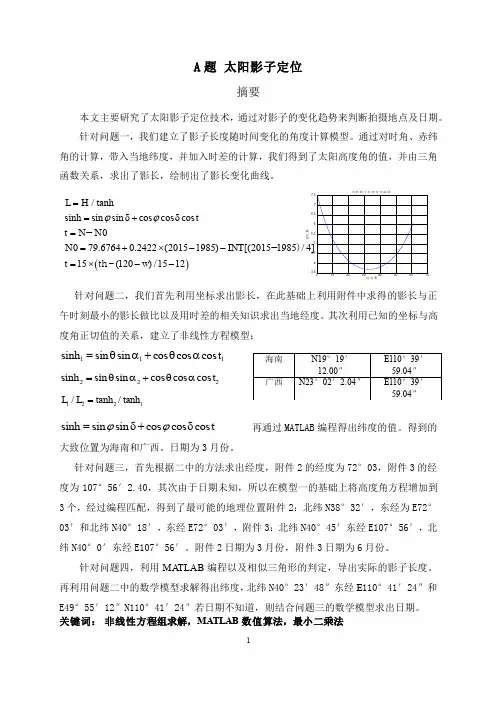
2015数学建模.

2015数学建模.

A 题 太阳影子定位摘要本文主要研究了太阳影子定位技术，通过对影子的变化趋势来判断拍摄地点及日期。

针对问题一，我们建立了影子长度随时间变化的角度计算模型。

通过对时角、赤纬角的计算，带入当地纬度，并加入时差的计算，我们得到了太阳高度角的值，并由三角函数关系，求出了影长，绘制出了影长变化曲线。

针对问题二，我们首先利用坐标求出影长，在此基础上利用附件中求得的影长与正午时刻最小的影长做比以及用时差的相关知识求出当地经度。

其次利用已知的坐标与高度角正切值的关系，建立了非线性方程模型：111sinh sin sin cos cos cos t =θα+θα 222sinh sin sin cos cos cos t =θα+θα1221/tanh /tanh L L =sinh sin sin cos cos cos t ϕϕ=δ+δ 再通过MATLAB 编程得出纬度的值。

得到的大致位置为海南和广西。

日期为3月份。

针对问题三，首先根据二中的方法求出经度，附件2的经度为72°03，附件3的经度为107°56′2.40，其次由于日期未知，所以在模型一的基础上将高度角方程增加到3个，经过编程匹配，得到了最可能的地理位置附件2：北纬N38°32′，东经为E72°03′和北纬N 40°18′，东经E72°03′，附件3：北纬N 40°45′东经E 107°56′，北纬N 40°0′东经E 107°56′。

附件2日期为3月份，附件3日期为6月份。

针对问题四，利用MA TLAB 编程以及相似三角形的判定，导出实际的影子长度。

再利用问题二中的数学模型求解得出纬度，北纬N 40°23′48″东经E 110°41′24″和E49°55′12″N110°41′24″若日期不知道，则结合问题三的数学模型求出日期。

2015年全国大学生数学建模竞赛A题秀论文介绍

2015年全国大学生数学建模竞赛A题秀论文介绍
8
7
7
6
6
太 阳 影 子 的 长 度 （m)
太 阳 影 子 的 长 度 （m)
5
5
4
4
3
3
2
2
1 -60
-40
-20 0 20 观测点的纬度（角度）
40
60
1 -25
-20
-15
-10 -5 0 5 10 太阳直射点的纬度（角度）
15
20
25
图 4 直杆影长与观测点纬度关系图
图 5 直杆影长与太阳直射点纬度的关系图
5
观测点与太阳直射点的经度差 进行灵敏度分析，分别分析改变此变量对直杆影 子长度的影响。 直杆影长与观测点纬度关系图如图 4 所示（图 4 为 11:00 时的关系图像） 。当 观测点纬度从南往当前的太阳高度角所在纬度靠近时，影长缩短，当观测点纬度 与太阳高度角处于同一纬度时，影长达到最小，随后观测点再往北移动，影长又 呈增大趋势，且增大速率明显加快。由图，在其他影响因素的取值都不变的前提 下，观测点纬度与太阳高度角处于同一纬度时，影长为 1m 左右，据推测， 12:00 时的图像，最小值应为 0m ，为太阳直射的情况。 直杆影长与太阳直射点纬度的关系图如图 5 所示。首先，太阳直射点的纬度 范围在南北回归线之间，而题设天安门所处的纬度在北回归线以北，故太阳直射 点纬度在由南到北的过程中，影长一直是减小的，且减小速率逐渐趋缓。
图 2 地球上过 A ， B 的大圆
考虑到太阳与地球之间相距较远，我们认为同一时刻照射到地球表面的太阳 光线是平行的，即 HF / / BO ，从而 AOB AHF 。
A 地 t 时刻的太阳高度角记为 angel 90 。
设图 1 中向量 AK 是与 A 点处经线相切且方向向北的单位向量，向量 AE 是与

2015数学建模获奖论文A题

2015数学建模获奖论文A题
②6 月 22 日，太阳直射北回归线，北回归线及其以北各地的正午太阳高度 达到全年最大，其日影也达到全年最短。
③6 月 22 日—12 月 22 日，在太阳直射点向南移动过程中，北回归线及其 以北各地的正午太阳高度逐渐减小，那么其日影逐渐增长；
④12 月 22 日，太阳直射南回归线，北回归线及其以北各地的正午太阳高度 达到全年最小，其日影也达到全年最长。
一年中，各地的日影长度会随季节变化而变化，这种变化主要体现在正午的 日影长短上。它与当地的正午太阳高度有直接关系：正午太阳高度越大，日影越 短；正午太阳高度越小，日影越长。例如：
①12 月 22 日—6 月 22 日，在太阳直射点向北移动过程中，北回归线及其以 北各地的正午太阳高度逐渐增大，那么其日影逐渐缩短；
图 4 天安门广场 15 年 10 月 22 日影子长度随时间(9 点到 15 点)变化图
在该问题中，影子长度的变化曲线根据计算出是一个关于真太阳时 12 点对 称的二次函数拟合曲线，所以我们利用题中所给的时间数据运用 MATLAB（附 录二）求解该附件的拟合曲线的表达式为
l(t) = 0.3179 t2 - 7.7982t + 51.4250
对于地球上的某个地点，太阳高度角是指太阳光的入射方向和地平面之间的 夹角，专业上讲太阳高度角是指某地太阳光线与通过该地与地心相连的地表切线 的夹角。太阳高度角简称高度角。当太阳高度角为 90°时，此时太阳辐射强度 最大；当太阳斜射地面时，太阳辐射强度就小。
图 1 太阳高度角示意图
太阳方位角即太阳所在的方位，指太阳光线在地平面上的投影与当地经线的 夹角，可近似地看作是竖立在地面上的直线在阳光下的阴影与正南方的夹角。方 位角以目标物正北方向为零，顺时针方向逐渐变大，其取值范围是 0—360°。 因此太阳方位角一般是以目标物的北方向为起始方向，以太阳光的入射方向 为 终止方向，按顺时针方向所测量的角度。

2015年全国大学生数学建模竞赛A题国赛一等奖

2015年全国大学生数学建模竞赛A题国赛一等奖

二、问题分析
2.1 概论 根据太阳影子定位技术确定视频中物体位置和日期， 这是一个涉及图像处理的最优 化问题。问题涉及地理、物理、数学等多学科知识，问题难点在于太阳影子定位过程涉 及多个参数的彼此关联，通过拟合确定变量。问题特点在于对涉及视频图像的处理，提 取关键性信息。 2.2 问题一 问题一要求建立影子长度变化的数学模型，通过查阅太阳影子定位技术的相关资 料，我们了解到影子的长度变化与物体高度、经度、纬度、时间、日期等参数密切相关。 因此解决问题一的关键在于确定与影子长度变化有关的参数以及影长和参数的关系， 建 立影子长度关于各参数的关系模型。以此分析影子长度关于各参数的变化规律，并代入
=39.9072 /180=10.6962rad
根据地球经度差与时间差的关系，当北京时间 H 为 9:00,当地时间(以时表示) h=9-4/60 (120-116.3914)=8 .7594 换算成具体时间为 8:45:33。 同理，北京时间 H 为 15:00 时，当地时间 ( 以时表示 )h= 14.7594 ，换算成具体时间为 14:45:33。综上可知时角 (360 / 24) ( h 12) ，h 为 8:45:33-14:45:33。 3.影长的计算 将相关参数代入公式（7），得到
实例计算。 2.3 问题二 问题二给出杆的影子顶点坐标，要求确定杆的地理位置。由于杆的高度未知，单独 应用问题一的模型难以解决问题二。因此，我们考虑在杆高度未知情况下，可通过太阳 方位角相关知识，以影长与太阳方位角和影子顶点坐标的关系，结合所给实际数据以杆 的经纬度为所求量，进行拟合，分析杆的地理位置。 2.4 问题三 问题三要求根据直杆在太阳下的影子长度端点坐标数据， 确定直杆所处的地点和日 期。地点、日期、杆高均未知，与问题二类似，所以考虑应用问题二的拟合算法，建立 优化模型，确定未知的各个参数值。 2.5 问题四 问题四要求确定视频的拍摄日期与地点， 日期未知时可以根据视频中直杆的影子变 化用问题三的模型求解，日期已知时可用问题二的模型求解。但由于所需影子信息都存 储在视频图像中，首先需要对视频图像进行处理，提取每帧画面中影子的长度、时间等 信息。之后用优化模型进行求解。

2015年全国大学生建模大赛A题太阳影子的定位

2015年全国大学生建模大赛A题太阳影子的定位

太阳影子定位摘要本文通过分析物体的太阳影子变化,利用太阳影子定位技术建立确定视频拍摄的地点与日期的模型。

针对问题一,首先通过分析知影子长度的变化主要影响参数为:当地的经度 λ、纬度ϕ、时刻t 、直杆长度l 、季节J (日期N )等,引入地理学参数:太阳赤纬δ、时角α及太阳高度角h 0,建立一个能够刻画影子长度变化与各个参数间关系的模型:⎪⎪⎩⎪⎪⎨⎧=⎥⎦⎤⎢⎣⎡⋅⋅-+-=h l h l t 000tan )cos cos sin sin sin arccos(300151δϕδϕλ;其次以实例对模型进行检验,在误差可允许的范围内,认为模型正确;进而对模型采用控制变量法分析影子长度关于各个参数的变化规律;然后求解出满足条件影子长度12时15分就是最短,大约3、674米(表3)。

影子长度的变化曲线(图5),9时至12时15分影子长度呈现下降趋势,12时15分之15时影子长度呈现上升趋势;最后考虑太阳照射中发生折射现象的推广。

针对问题二,关键词一、问题重述:如何确定视频的拍摄地点与拍摄日期就是视频数据分析的重要方面,太阳影子定位技术就就是通过分析视频中物体的太阳影子变化,确定视频拍摄的地点与日期的一种方法。

1、建立影子长度变化的数学模型,分析影子长度关于各个参数的变化规律,并应用您们建立的模型画出2015年10月22日北京时间9:00-15:00之间天安门广场(北纬39度54分26秒,东经116度23分29秒)3米高的直杆的太阳影子长度的变化曲线。

2、根据某固定直杆在水平地面上的太阳影子顶点坐标数据,建立数学模型确定直杆所处的地点。

将您们的模型应用于附件1的影子顶点坐标数据,给出若干个可能的地点。

3、根据某固定直杆在水平地面上的太阳影子顶点坐标数据,建立数学模型确定直杆所处的地点与日期。

将您们的模型分别应用于附件2与附件3的影子顶点坐标数据,给出若干个可能的地点与日期。

4.附件4为一根直杆在太阳下的影子变化的视频,并且已通过某种方式估计出直杆的高度为2米。

2015年全国大学生数学建模竞赛A题

2015年全国大学生数学建模竞赛A题

太阳影子定位（一）摘要根据影子的形成原理和影子随时间的变化规律，可以建立时间、太阳位置和影子轨迹的数学模型，利用影子轨迹图和时间可以推算出地点等信息，从而进行视频数据分析可以确定视频的拍摄地点。

本文根据此模型求解确定时间地点影子的运动轨迹和对于已知运动求解地点或日期。

直立杆的影子的位置在一天中随太阳的位置不断变化，而其自身的所在的经纬度以及时间都会影响到影子的变化。

但是影子的变化是一个连续的轨迹，可以用一个连续的函数来表达。

我们可以利用这根长直杆顶端的影子的变化轨迹来描述直立杆的影子。

众所周知，地球是围绕太阳进行公转的，但是我们可以利用相对运动的原理，将地球围绕太阳的运动看成是太阳围绕地球转动。

我们在解决问题一的时候，利用题目中所给出的日期、经纬度和时间，来解出太阳高度角ｈ，太阳方位角Α，赤纬角δ，时角Ω，直杆高度Ｈ和影子端点位置（x0，y o），从而建立数学模型。

影子的端点坐标是属于时间的函数，所以可以借助时间写出参数方程来描述影子轨迹的变化。

问题二中给出了日期和随时间影子端点的坐标变化，可以根据坐标变化求出运用软件拟合出曲线找到在正午时纵坐标最小，横坐标最大，影子最短的北京时间，根据时差与经度的关系，求出测量地点的经度。

根据太阳方位角Α，赤纬角δ，时角Ω，可以求出太阳高度角ｈ。

再结合问题一中的表达式，建立方程求解测量地点的纬度Ф。

我们在求解第三问的思路也是沿用之间的模型，但第三问上需要解出日期。

对于问题四的求解，先获取自然图像序列或者视频帧，并对每一帧图像检测出影子的轨迹点；然后确定多个灭点，并拟合出地平线；拟合互相垂直的灭点，计算出仿射纠正和投影纠正矩阵；进而还原出经过度量纠正的世界坐标；在拟合出经过度量纠正世界坐标中的影子点的轨迹，利用前面几问中的关系求出经纬度。

关键字：太阳影子轨迹Matlab曲线拟合（二）问题重述确定视频拍摄地点和拍摄日期是视频数据分析的重要方面，太阳影子定位技术就是通过分析视频中物体的太阳影子变化，确定视频拍摄的地点和日期的一种方法。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2015高教社杯全国大学生数学建模竞赛题目（请先阅读“全国大学生数学建模竞赛论文格式规范”）A题太阳影子定位如何确定视频的拍摄地点和拍摄日期是视频数据分析的重要方面，太阳影子定位技术就是通过分析视频中物体的太阳影子变化，确定视频拍摄的地点和日期的一种方法。

1.建立影子长度变化的数学模型，分析影子长度关于各个参数的变化规律，并应用你们建立的模型画出2015年10月22日北京时间9:00-15:00之间天安门广场（北纬39度54分26秒,东经116度23分29秒）3米高的直杆的太阳影子长度的变化曲线。

2.根据某固定直杆在水平地面上的太阳影子顶点坐标数据，建立数学模型确定直杆所处的地点。

将你们的模型应用于附件1的影子顶点坐标数据，给出若干个可能的地点。

3. 根据某固定直杆在水平地面上的太阳影子顶点坐标数据，建立数学模型确定直杆所处的地点和日期。

将你们的模型分别应用于附件2和附件3的影子顶点坐标数据，给出若干个可能的地点与日期。

4．附件4为一根直杆在太阳下的影子变化的视频，并且已通过某种方式估计出直杆的高度为2米。

请建立确定视频拍摄地点的数学模型，并应用你们的模型给出若干个可能的拍摄地点。

如果拍摄日期未知，你能否根据视频确定出拍摄地点与日期？太阳影子定位摘要本文通过分析物体的太阳影子变化，利用太阳影子定位技术建立确定视频拍摄的地点和日期的模型。

针对问题一，首先通过分析知影子长度的变化主要影响参数为：当地的经度λ、纬度ϕ、时刻t、直杆长度l、季节J（日期N)等，引入地理学参数：太阳赤纬δ、时角α及太阳高度角h 0，建立一个能够刻画影子长度变化和各个参数间关系的模型：⎪⎪⎩⎪⎪⎨⎧=⎥⎦⎤⎢⎣⎡⋅⋅-+-=h l h l t 000tan)cos cos sin sin sin arccos(300151δϕδϕλ；其次以实例对模型进行检验，在误差可允许的范围内，认为模型正确；进而对模型采用控制变量法分析影子长度关于各个参数的变化规律；然后求解出满足条件影子长度12时15分是最短，大约3.674米（表3）。

影子长度的变化曲线（图5），9时至12时15分影子长度呈现下降趋势，12时15分之15时影子长度呈现上升趋势；最后考虑太阳照射中发生折射现象的推广。

针对问题二，关键词 一、问题重述：如何确定视频的拍摄地点和拍摄日期是视频数据分析的重要方面，太阳影子定位技术就是通过分析视频中物体的太阳影子变化，确定视频拍摄的地点和日期的一种方法。

1.建立影子长度变化的数学模型，分析影子长度关于各个参数的变化规律，并应用你们建立的模型画出2015年10月22日北京时间9:00-15:00之间天安门广场（北纬39度54分26秒,东经116度23分29秒）3米高的直杆的太阳影子长度的变化曲线。

2.根据某固定直杆在水平地面上的太阳影子顶点坐标数据，建立数学模型确定直杆所处的地点。

将你们的模型应用于附件1的影子顶点坐标数据，给出若干个可能的地点。

3. 根据某固定直杆在水平地面上的太阳影子顶点坐标数据，建立数学模型确定直杆所处的地点和日期。

将你们的模型分别应用于附件2和附件3的影子顶点坐标数据，给出若干个可能的地点与日期。

4．附件4为一根直杆在太阳下的影子变化的视频，并且已通过某种方式估计出直杆的高度为2米。

请建立确定视频拍摄地点的数学模型，并应用你们的模型给出若干个可能的拍摄地点。

如果拍摄日期未知，你能否根据视频确定出拍摄地点与日期？二、问题分析：针对问题一，首先通过分析知影子长度的变化主要影响参数为：当地的经度λ、纬度ϕ、时刻t 、直杆长度l 、季节J （日期N )等，引入地理学参数：太阳赤纬δ、时角α及太阳高度角h 0，建立一个能够刻画影子长度变化和各个参数 间关系的模型；其次以实例对模型进行检验，在误差可允许的范围内，认为模型正确；进而根据所建模型分析影子长度关于各个参数的变化规律；然后做出影子长度的变化曲线；最后考虑太阳照射中发生折射现象的推广。

针对问题二，三、模型假设：1、求解此问题时忽略地球的自转2、不考虑太阳光线在穿过大气层时的折射、太阳的视面角、高山阻挡、海拔高度等因素。

3、认为照射到地球上的太阳光可以看成是平行光线，地球上某地的水平地面是地球球面上过该地的切面。

四、符号说明：δ：太阳赤纬 α：太阳时角ϕ：表示某地的地理纬度λ：表示某地的地理经度h：太阳高度角五、问题一的模型建立与求解5.1影响影子长度参数的确定 1、太阳赤纬太阳赤纬是地球赤道平面与太阳和地球中心的连线之间的夹角且以年为周期，在周年运动中任何时刻的赤纬值δ都是严格已知的，可用下式计算：）（13cos 0201.02cos 3656.0cos 758.03sin 1712.02sin 1149.0sin 2567.233723.0θθθθθθδ++--++= 式中θ称为日角，即2422.365/2t πθ=，这里0N N t -=,式中N 为积日，就是日期在年内的顺序号（例如1月1日其积日为1，平年1212月31日的积日为365，闰年则为366等）。

)4/9851-((-1985-2422.06764.790）年份）（年份INT N ⨯+=（式中INT 表示取整数部分）故如果已知某日期的年、月、日，代入式（1），即可求得此日期的太阳赤纬值δ。

2、时角时角表示一天体是否通过了当地的子午圈，其数值表示该天体与当地子午圈的角距离，并借用时间的单位以小时来计量，其中当地时间12点时的时角为零，令上午的时角为正，下午为负。

某地t 0的时角α计算式如下：故若给定某地时刻t 0的值，代入式（2），即可求出此时的时角值α3、太阳高度角太阳高度角,是指太阳光线与地平面的夹角。

应用球面三角形余弦公式A c b c b a cos sin sin cos cos cos +=，结合图形,可以推出任意时刻太阳高度角h 0的计算公式为：）（3cos )sin()sin()cos()cos()cos(90909090900αϕδϕδ--+--=-h进一步可以得到：）（4cos cos cos sin sin sin 0αϕδϕδ+=h 式中，ϕ表示当地的地理纬度,δ表示太阳赤纬，α表示太阳时角、h 0表示太阳高度角。

ϕ、δ的取值为北正南负。

故若已知某地的地理纬度ϕ、太阳赤纬δ、太阳时角α，代入式（4），即可求得太阳高度角。

4、直杆的长度直杆的影子始终在物体背着光源的一面，光从物体顶端照射到地面形成影子，直杆的长度l 0直接影响着影子长度的变化。

5.2模型一的建立首先分析影子长度变化直接受直杆长度l 0和太阳高度角h 0的影响，其关系式为：）（5tan 0h ll =其中l 表示影子的长度。

然后以太阳高度角与太阳赤纬、时角、地理纬度的关系为基础，即式（4），引进参数当地的经度，构建影子长度变化模型如下：)6(tan)cos cos sin sin sin arccos(300151000⎪⎪⎩⎪⎪⎨⎧=⎥⎦⎤⎢⎣⎡⋅⋅-+-=h l h l t δϕδϕλ式中λ、ϕ、δ、h 0、t 分别代表当地的经度、纬度、太阳赤纬、太阳高度角和时刻（北京时间）。

编写程序计算时注意到，当1cos cos sin sin sin 0≤⋅⋅-δϕδϕh 时，反余弦函数值才存在，应采用判断，当其大于t 时则进行下一个t 的计算。

5.3模型一的检验以实际某地情况为例，已知当地的经度为，纬度为，5.4影子长度关于各个参数的变化规律根据影子长度变化模型，以影子长度l为因变量，依次选择各个参数为自变量，其余参数看为固定值，进而描述出影子长度关于各个参数变化规律。

1、影子长度关于直杆长度的变化规律以直杆长度l0为自变量，以影子长度为因变量，太阳高度角h0为固定值，取直杆长度为50米，间隔为0.5米，根据公式（5），得到h0与l0之间的关系，~画出关系图像如图1：由图1我们可以很直观的的看出，在其他参数不变时，直杆长度越长，影子长度越长，且两者的比值是不变的。

2、影子长度的日变化规律以每日的时间t作为自变量，影子长度为因变量，其它参数为固定值，取为2015年10月22日北京时间8:00-16:00之间天安门广场（北纬39度54分26秒,东经116度23分29秒）3米高的直杆，根据公式（6），得到影子长度的日变化规律。

由于地球是个固体球,且自西向东自转,因此太阳高度也呈现出与之对应的日变化规律:地球上观察太阳为东升西落,早晨太阳从东方地平线上升起,晨昏线上太阳高度为0 ，随着太阳的逐渐升高,太阳高度是逐渐增大的，影子的长度逐渐减小。

当某地经线正对太阳光时,地方时为正午12点，即为北京时间12时15分,此时太阳高度角达到一天中的最大，影子长度最小。

之后太阳逐渐西落,太阳高度也慢慢变小，影子逐渐变长,到西方地平线落下时,没有影子。

3、影子长度随纬度变化规律以纬度 作为自变量，影子长度为因变量。

其它参数为固定值，由于正午太阳高度角最能反映太阳辐射的强弱变化,故取2015年10月22日北京时间12时东经116度23分29秒3米高的直杆，根据公式（6），得到影子长度的随纬度的变化规律。

正午太阳高度由直射点向南北两侧递减，故影子长度由直射点向南北两侧递增。

夏至:6223'+=ϕ，影子长度从北回归线向南北两侧递增;同样冬至:6223-'= ϕ，影子长度从南回归线向南北两侧递增;春秋分:0=ϕ，影子长度从赤道向南北两侧递增,且离直射点距离越近,与直射点纬度差越小,影子长度就越小。

4、影子长度随季节的变化规律 以季节作为自变量，影子长度为因变量。

由于正午太阳高度角最能反映太阳辐射的强弱变化,故取2015年北京时间12时天安门广场（北纬39度54分26秒,东经116度23分29秒）3米高的直杆，根据公式（6），得到影子长度的随季节的变化规律。

北回归线及以北地区,6月22日正午太阳高度达一年中最大值，此时影子长度最小,12月22日达一年中最大值;南回归线以南地区,12月22日达一年中最小值,6月22日达一年中最大值;南北回归线之间,一年中因有两次太阳直射机会,赤道至北回归线之间12月22日的正午影子长度达一年中最大值,而赤道至南回归线之间6月22日达一年中最大值。

5.5问题一的求解求解步骤：1）将2015年10月22日北京时间9:00-15:00之间天安门广场（北纬39度54分26秒,东经116度23分29秒）3米高的直杆符号化为907.39+=λ，491.116=ϕ，30=l ；2）计算太阳赤纬：已知年份为2015年，积日为295，代入公式得：9424.79)4/9851-((-1985-2422.06764.790=⨯+=）年份）（年份INT N067.2150=-=N N t6996.32422.365/2==t πθ8627.10-3cos 0201.02cos 3656.0cos 758.03sin 1712.02sin 1149.0sin 2567.233723.0=++--++=θθθθθθδ得到太阳的赤纬角为8627.10-3）计算太阳时角：需将当地时间转化为北京时间，对应北京时间t ，将t得到2015年10月22日北京时间天安门广场时角值（如表1），其中907.39+=λ。