下载文档原格式
简单地说，AP微积分是一门大学入门级别的微积分课程。
学生会在探索变化、极限、方程等概念的过程中学习掌握相关定义、定理的论证和总结。
学生需要通过图像、数字、分析和语言描述来解决实际问题，并在此过程中培养强化对于微分学和积分学的理解。
AP微积分课程分为AP Calculus AB和AP Calculus BC两种，两者是被包含与包含的关系，即BC是AB的拓展与延伸。
二者共同包括的内容有极限、导数、定积分、牛顿-莱布尼兹公式、微分方程等课题，而专属于BC的内容有参数方程、矢量方程、极坐标、无限序列、级数等课题。
从另一个角度来说，微积分AB所涵盖的内容大约是美国大学一个学期所教授的微积分知识，而微积分BC所涵盖的内容差不多要一个学年才能上完。
具体的课程设置参见下表（其中九、十单元的所有内容以及六、七、八单元中的部分内容为BC课程独有）：不过虽然大纲版本在变化，可喜可贺的是考试内容并无翻天覆地的变化。
对于课程学校中计算器问题，一般要求所使用的图形计算器一定能够画函数图像，条件允许情况下最好准备TI-Nspire系列(推荐CX-CAS)。
而且图形计算器在美国大学很多课程都要用到，可提前准备着。
希望以上的内容能给将要学习AP微积分的同学们一点帮助。
学通国际课程培训中心自2008年起一直致力于ALEVEL、IGCSE、IB、AP、SAT2等主流国际课程中30多门科目的提分与培优，经11年深耕教学，目前已拥有教师团队80余人，其中20%为博士，80%为名校海归硕士，平均国际课程教龄8年以上，每年为学生提供50000小时以上的高品质课程。
除常规国际课程培训外，我们还提供“G5全程护航计划”——全天候全脱产式学习，“全球TOP10大学冲击计划”——高考留学两不误双轨制ALEVEL课程，国际学校备考与衔接课程，英国G5名校STEP、MAT、PAT、TSA、牛剑面试等附加考试辅导，海外学校iTEP、Ukiset、AEAS、AEIS、维立克面试等入学考试辅导课程；同时还提供个性化的学术背景提升项目。
A P微积分满分考生的备考方法Prepared on 24 November 2020AP微积分满分考生的备考方法AP微积分作为美国大学一年级的数学课，大部分高中都会都接触微积分，并且我国高中的数学要求高于美国。
所以小编建议学习AP微积分建议跟老师学习，因为它毕竟是一门课程。
小编在这里和大家分享一篇来自AP微积分BC5分学霸的备考心得，希望能够给到正在积极备考AP微积分BC的同学帮助。
AP微积分BC简介AP考试一向都是大学Introduction等级的课程。
微积分AB对应第一门课程Calculus1，只考察最基础的求极限，求导，积分。
而微积分BC实际上却对应数学的第二门课程，比起微积分AB多考察了少许知识点比如分步积分，包含参数方程，极坐标的微积分问题，微分方程，泰勒级数。
最好的是，微积分BC包含了微积分AB的课程，考完了附送微积分AB成绩所以可以一起换8个学分。
微积分BC考试分为2个section 4个部分 Section1为多项选择， A部分不可用计算器，限时55分钟，28题，B部分可以用计算机，限时50分钟，17题。
Section 2为大题，A部分可以用计算机，有两道题限时30分钟，B部分不能用计算机，有四道题合计60分钟。
学习AP微积分的好处1】AP学习节省时间首先，对于工程系undergraduate student来说，以Georgia tech佐治亚理工为例，大学期间一般只用学习5门数学课分别是Calculus 1(最简单的求导，积分对应Calculus AB) ,Calculus 2(对应calculus BC，和Calculus1合起来对应同济大学高等数学上，但泰勒技术包括在高等数学下册里)，linear algebra 线性代数，Multivariable Calculus 多元微积分(对应同济大学高等数学下)，和一门专门的Differential Equation 微分方程课。
超实用的AP微积分备考和考试信息AP微积分作为美国大学一年级的数学课，大部分高中都会都接触微积分，并且我国高中的数学要求高于美国。
所以小编建议学习AP微积分建议跟老师学习，因为它毕竟是一门课程。
一、AP微积分简介AP微积分中国学生最擅长的考试科目之一，也是历年报名人次最多的AP考试科目。
微积分在物理、经济学、金融学、精算学、管理学等学科中都有广泛运用，是美国大学中的基础课程之一。
AP微积分包括AP微积分BC和AP微积分AB两个科目，其知识深度和知识结构相当于美国大学一年级的微积分(仅限于单变量微积分)，是所有AP科目中语言对其影响最小的课程。
AP微积分BC包含AP微积分AB的全部内容，所以考BC会同时给出AB子分数。
虽然AP微积分BC的知识点比微积分AB多，难度更高，但是AP微积分BC的受认可度更高，也更容易换取学分。
AP成绩一般大学3分及以上就可折抵学分(各学校有转换学分的具体规定)，一般情况正确率在65%以上可确保5分。
对绝大部分中国AP考生来说，AP微积分BC的难度并不高，中国考生一般高一或者高二的时候就会开始准备AP微积分的考试，因此大多数理工科学生只要时间充裕都会直接考BC，文科类学生根据高中数学基础选择考BC或者AB。
二、AP微积分考试试卷题型结构与分数计算AP微积分BC和AP微积分AB两门考试满分都是108，卷面分与5分制的兑换每年划分的分数区间都不一样，但一般来说，108分超过70就可以得5分，大致就是100分考得60分，还是比较宽松的。
由于自由问答题部分比选择题部分难，因此选择题的错误个数要有一定控制。
一般来说，选择题错误需控制在15题以内，可以拿5分，但是为了确保高分，我们建议以5分为目标的同学，选择题需控制在10道题以内。
从以往的教学和考生经历来看，中国学生得5分的概率在70%以上，3分及以下的成绩相当罕见。
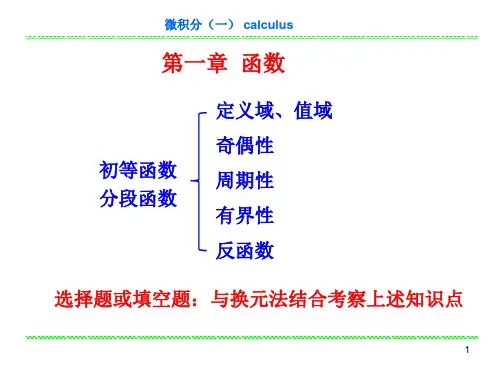
三、AP微积分卷面分数与5分制给分比例四、AP微积分中的高中知识AP微积分中用到的高中知识主要是函数相关知识，主要有以下几方面内容：函数的定义、函数的图像、分段函数、绝对值函数、定义域和值域等函数的运算及复合函数，函数图像的对称性x的n次幂的函数、反比例函数、多项式函数、有理函数、三角函数的定义、性质和图像分析反函数和反三角函数的图像和性质指数函数和对数函数参数方程200个AP微积分常用词汇absolutely convergent ,adj 绝对收敛antiderivative ,n 不定积分binomial theorem ,n 二项式定理，二项展开式chain rule ,n 链规则calculus ,n 微积分学conditionally convergent ,adj 条件收敛continuity ,n 连续converge ,v 收敛definite integral ,n 定积分derivative ,n 导数differential coefficient ,n 微分differential equation ,n 微分方程directional derivative ,n 方向导数diverge ,v 发散divergence ,n 散度gradient ,n 梯度implicit differentiation ,n 隐函数微分implicit function ,n 隐函数improper integral ,n 广义积分integrable ,adj 可积的integral ,n 积分integration by parts ,n 部分积分法left-hand limit ,n 左极限limit ,n 极限local maximum ,n 极大值local minimum ,n 极小值method of lagrange multipliers ,n 拉格朗日乘数法multiple integral ,n 多重积分partial derivative ,n 偏导数polar coordinates ,n 极坐标power series ,n 幂级数right-hand limit ,n 右极限rotation ,n 旋度series ,n 级数substitution rule ,n 替代法则table of integrals ,n 积分表taylor’s formula ,n 泰勒公式three-dimensional analytic geometry ,n 空间解析几何total differential ,n 全微分trigonometric substitution ,n 三角替代法absolutely convergent 绝对收敛absolute value 绝对值algebraic function 代数函数analytic geometry 解析几何antiderivative 不定积分approximate integration 近似积分approximation 近似法、逼近法arbitrary constant 任意常数arithmetic series/progression (AP)算数级数asymptotes (vertical and horizontal)(垂直/水平)渐近线average rate of change 平均变化率base 基数binomial theorem 二项式定理，二项展开式Cartesian coordinates 笛卡儿坐标(一般指直角坐标) Cartesian coordinates system 笛卡儿坐标系Cauch’s Mean Value Theorem 柯西均值定理chain rule 链式求导法则calculus 微积分学closed interval integral 闭区间积分coefficient 系数composite function 复合函数conchoid 蚌线continuity (函数的)连续性concavity (函数的)凹凸性conditionally convergent 有条件收敛continuity 连续性critical point 临界点cubic function 三次函数cylindrical coordinates 圆柱坐标decreasing function 递减函数decreasing sequence 递减数列definite integral 定积分derivative 导数determinant 行列式differential coefficient 微分系数differential equation 微分方程directional derivative 方向导数discontinuity 不连续性discriminant (二次函数)判别式disk method 圆盘法divergence 散度divergent 发散的domain 定义域dot product 点积double integral 二重积分ellipse 椭圆ellipsoid 椭圆体epicycloid 外摆线Euler's method (BC)欧拉法expected valued 期望值exponential function 指数函数extreme value heorem 极值定理factorial 阶乘finite series 有限级数fundamental theorem of calculus 微积分基本定理geometric series/progression (GP)几何级数gradient 梯度Green formula 格林公式half-angle formulas 半角公式harmonic series 调和级数helix 螺旋线higher derivative 高阶导数horizontal asymptote 水平渐近线horizontal line 水平线hyperbola 双曲线hyper boloid 双曲面implicit differentiation 隐函数求导implicit function 隐函数improper integral 广义积分、瑕积分ncrement 增量increasing function 增函数indefinite integral 不定积分independent variable 自变数inequality 不等式ndeterminate form 不定型infinite point 无穷极限infinite series 无穷级数infinite series 无限级数inflection point (POI) 拐点initial condition 初始条件instantaneous rate of change 瞬时变化率integrable 可积的integral 积分integrand 被积分式integration 积分integration by part 分部积分法intercept 截距intermediate value of Theorem ：中间值定理inverse function 反函数irrational function 无理函数iterated integral 逐次积分Laplace transform 拉普拉斯变换law of cosines 余弦定理least upper bound 最小上界left-hand derivative 左导数left-hand limit 左极限L'Hospital's rule 洛必达法则limacon 蚶线linear approximation 线性近似法linear equation 线性方程式linear function 线性函数linearity 线性linearization 线性化local maximum 极大值local minimum 极小值logarithmic function 对数函数MacLaurin series 麦克劳林级数mean value theorem (MVT)中值定理minimum 最小值method of lagrange multipliers 拉格朗日乘数法modulus 绝对值multiple integral 多重积分multiple 倍数multiplier 乘子octant 卦限open interval integral 开区间积分optimization 优化法，极值法origin 原点orthogonal 正交parametric equation (BC)参数方程partial derivative 偏导数partial differential equation 偏微分方程partial fractions 部分分式piece-wise function 分段函数parabola 抛物线parabolic cylinder 抛物柱面paraboloid ：抛物面parallelepiped 平行六面体parallel lines 并行线parameter ：参数partial integration 部分积分partiton ：分割period ：周期periodic function 周期函数perpendicular lines 垂直线piecewise defined function 分段定义函数plane 平面point of inflection 反曲点point-slope form 点斜式polar axis 极轴polar coordinates 极坐标polar equation 极坐标方程pole 极点polynomial 多项式power series 幂级数product rule 积的求导法则quadrant 象限quadratic functions 二次函数quotient rule 商的求导法则radical 根式radius of convergence 收敛半径range 值域(related) rate of change with time (时间)变化率rational function 有理函数reciprocal 倒数remainder theorem 余数定理Riemann sum 黎曼和Riemannian geometry 黎曼几何right-hand limit 右极限Rolle's theorem 罗尔(中值)定理root 根rotation 旋转secant line 割线second derivative 二阶导数second derivative test 二阶导数试验法second partial derivative 二阶偏导数series 级数shell method (积分)圆筒法sine function 正弦函数singularity 奇点slant 母线slant asymptote 斜渐近线slope 斜率slope-intercept equation of a line 直线的斜截式smooth curve 平滑曲线smooth surface 平滑曲面solid of revolution 旋转体symmetry 对称性substitution 代入法、变量代换tangent function 正切函数tangent line 切线tangent plane 切(平)面tangent vector 切矢量taylor's series 泰勒级数three-dimensional analytic geometry 空间解析几何total differentiation 全微分trapezoid rule 梯形(积分)法则。
AP微积分核心内容AP微积分核心内容AP微积分的核心内容介绍。
AP微积分考试包括微积分AB (Calculus AB) 和微积分BC(Calculus BC)两门课。
AP微积分AB需要1年的课程学习时间，其内容大约占了大学一年的微积分课程内容的三分之二，而AP微积分BC需要1年多的课程学习时间。
下面我们从AP 微积分考核的四个方面内容来看极限在其中的表现。
1、极限和函数的连续：函数在某一点存在极限的充要条件是左极限与右极限均存在且相等。
可用极限判断函数是否存在渐近线(竖直渐近线、水平渐近线)：由此分析函数的基本特征。
?用极限来定义函数在某点的连续性：夹挤定理、中间值定理、极值定理都是极限概念的延展。
2、导数、微分及应用：对瞬时变化率问题如速度、加速度等的研究产生了导数。
其几何意义是函数f(x)在a点的斜率。
由此可讨论连续函数的增减性、弯凸性、确定函数极值、相关变化率。
并可由导数定义式给出所有函数的求导公式。
3、定积分、不定积分及应用：对非常规图形面积的计算的要求产生了定积分。
“分割、近似求和(黎曼和)、取极限(定积分)”是定积分的核心思想。
4、多项式近似和无穷级数：无穷级数是微积分学的重要组成部分，涉及极限、微分和积分的内容。
级数收敛、发散的定义。
三立在线课程培训优势班级种类：（预约试听和科学选班请详询老师）一对一在线授课班，其优势：一对一是指听说读写都由不同的老师教授，而不是由一位老师负责学生的全部课程。
再加上督导顾问，总共是5位老师服务1位学员。
一对一可以依据学生自身的优势弱势打造独一无二的学习计划，既避免了已熟悉知识点的无意义重复，又不会将学生还没掌握的重点难点一带而过。
这不但大大节约了学习时间，提高了学习效率，而且又有人随时督促，提高学习积极性。
同时在线授课突破时空限制，再忙的学员都能将有限的空闲时间利用起来；异地学员也能享受到海外名师授课，这在传统教学中是无法做到的。
另外托福本身就是机考，平时在网络上上课，更有助于提前考试演练，熟悉考试流程。
2024 AP Calculus AB历年题目精粹在2024年的AP Calculus AB考试中，历年的题目一直是备考的重要内容。
通过分析历年的题目，我们可以更好地了解该科目的考察点和难点，为备考提供有力的参考。
本文将对2024年AP Calculus AB历年题目进行精选和整理，以便学生们更好地备考。
第一部分：选择题选择题是AP Calculus AB考试中的常见题型，涵盖了课程的各个知识点。
以下是2024年AP Calculus AB选择题中的精选题目。
题目一：设函数f(x) = (x^3 - 9x^2 + 15x - 7)^{\frac{1}{3}}，则f'(x)等于：A. 3x^2 - 18x + 15B. 3x^2 - 14xC. 3x^2 - 6x + 5D. 3x^2 - 6x - 2E. 3x^2 - 11x - 2题目二：已知函数f(x) = e^x，g(x) = \ln(x + 1)，则f(g(e))的值为：A. 1B. eC. e^2D. e^xE. 0题目三：对于函数f(x) = \frac{2}{x + 1}，以下哪个区间上f(x)是严格递增的？A. (-\infty, -1)B. (-1, 0)C. (0, 1)D. (1, \infty)E. (-\infty, \infty)第二部分：解答题解答题是AP Calculus AB考试中的较为复杂的题型，要求学生理解问题并进行完整的解答。
以下是2024年AP Calculus AB解答题中的精选题目。
题目一：已知曲线y = x^2 + 2x，求曲线与x轴之间的面积。
题目二：已知函数f(x) = 2x^3 - 3x^2 - 12x + 5，求f'(x)的零点。
题目三：已知函数f(x) = \frac{1}{2}x^2 - 2x + 4，求f(x)的极大值和极小值点。
第三部分：综合题综合题是AP Calculus AB考试中的综合考察题型，要求学生综合运用所学的知识和技巧进行解答。
ap微积分知识点
AP微积分是高中阶段的一门课程，主要介绍微积分的基本概念和应用。
以下是一些AP微积分的知识点：
1. 导数：导数是函数在某一点的变化率，也可以理解为函数曲线在该点的切线斜率。
常见的导数计算法则包括求常数函数、幂函数、指数函数、对数函数、三角函数等的导数。
2. 微分：微分是导数的另一种表达方式，表示函数在某一点附近的近似线性变化量。
微分可以帮助我们研究函数的极值、曲线的凹凸性等性质。
3. 积分：积分是导数的逆运算，表示函数的累积效应。
通过积分可以计算曲线下的面积、变化量等。
常见的积分计算方法包括不定积分和定积分。
4. 不定积分：不定积分是求导的逆运算，表示函数的原函数。
不定积分的结果通常有一个常数项。
5. 定积分：定积分是计算函数在给定区间上的累积效应，表示曲线下的面积。
定积分可以通过反向求导的方式来计算。
6. 牛顿-莱布尼茨公式：牛顿-莱布尼茨公式是微积分的基本定理之一，它将积分和导数联系在一起。
该公式表明，函数的原函数与其在某一区间上的定积分之间存在关系。
7. 泰勒级数：泰勒级数是一种将函数展开成无穷级数的方法，可以用来近似表示复杂函数。
通过泰勒级数展开，我们可以研究函数的性质和计算函数的近似值。
以上是AP微积分的一些基本知识点，它们构成了微积分的核心内容。
掌握这些知识点能够帮助我们理解函数的变化规律、求解问题以及应用到实际生活中的各种情境中。
AP微积分BC（包含AB）考点梳理嗨，少年/少女，无论你是自学的，还是在哪里学的，学完AP微积分AB或者BC，在你“婶婶”的脑海里应该有的知识框架是：函数的极限是什么概念，基本的计算方法和逻辑是怎样的；什么叫函数的连续，闭区间连续的函数有什么性质；导数是什么，有哪些常见的计算方法，有哪些基本应用；积分里的定积分和不定积分各自是什么，怎么计算，有什么应用；无穷级数是什么鬼，什么叫做无穷级数的收敛/发散，常见的无穷级数有哪些，常见判断无穷级数是否收敛的方法有哪些；幂级数是什么鬼，什么是它的收敛域（半径）；泰勒级数/泰勒多项式是啥，用泰勒多项式进行估算时，误差边界怎么算。
具体要求内容如下：1.极限（Limits）1)极限定义的理解极限的逻辑，左右极限的概念以及此基础上的极限存在原则；还需要会从图像上判断极限。
2)基本计算一些基本函数的极限结论要熟悉，如y=e!在x分别趋向于正无穷、负无穷时的极限，y=sin x在x趋向于无穷大时的极限，等等；基本的加减乘除原则；有理函数类型（自变量趋向于无穷时，直接看最高项次方的关系，包括 e 3x!e!2x2e!e这种类似形式的）；两个极限小公式（一个是sin x/x，一个是结果记为e的那个）；洛比达法则（L’ Hopital’s Rule）——AB暂时不考——BC考极限喜欢考它。
3)求函数渐近线水平的和竖直的各自用极限是怎么定义计算的，基础还是极限计算。
不要死背公式，回到逻辑上去看。
2.连续（Continuity）1)连续的定义包括在一点的连续和在一个区间的连续的定义，以及如何根据定义去判断函数在一点是否连续（包括代数计算和根据图像的判断）。
2)闭区间连续函数的性质定理最值定理（Extreme Value Theorem）介值定理（Intermediate Value Theorem）零点定理（Zero Point Theorem）记住这三个定理的内容，理解其逻辑，并会联系Mean Value Theorem。
ap微积分ab容错率
AP微积分AB考试，全称为Advanced Placement Calculus AB，是美国大学预修课程中的一门学科。
AP微积分AB考试旨在检验学生对于微积分的理解和应用能力，其容错率是指在考试中，学生在出现错误时仍能获得部分分数的机制。
AP微积分AB考试的容错率通常为20%，即只需要达到卷面总分的80%即可得到满分5分。
然而，这个容错率并不是绝对的，具体情况还需要根据实际考试题目和评分标准来确定。
在AP微积分AB考试中，由于知识点繁多复杂，数学专有名词多，且校内课程进度飞快，学生往往缺乏复习巩固的专项练习，这使得考试难度较大。
同时，由于容错率的设置，学生在考试中也需要有一定的策略。
比如，在遇到困难的问题时，可以考虑放弃直接跳过，先完成其他较为容易的问题，最后再回过头来解决这个问题。
这样可以避免因为过于纠结于一个难题而浪费时间，从而影响整体的答题效果。
另外，需要注意的是，不同科目的容错率是不同的。
在AP微积分考试中，AB和BC两个科目的容错率也有所差异。
根据近年的数据，AP微积分BC的容错率为15%，而AB的容错率为20%。
这表明，在微积分BC考试中，学生需要更加精确地掌握知识点，才能获得高分。
总之，对于准备参加AP微积分AB考试的学生来说，需要充分了解考试的容错率情况，制定合理的答题策略，掌握知识点并保持冷静的心态。
这样才能在考试中发挥出自己的最佳水平，获得满意的成绩。
