SPC基础控制图
- 格式:pdf
- 大小:485.60 KB
- 文档页数:10

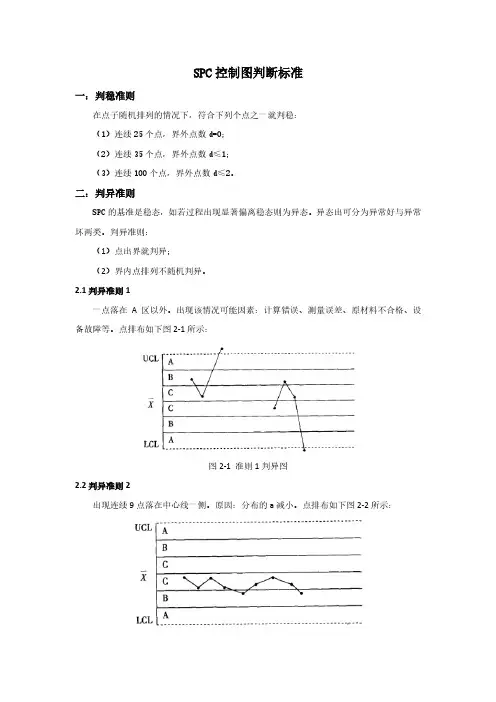
SPC控制图判断标准一:判稳准则在点子随机排列的情况下,符合下列个点之一就判稳:(1)连续25个点,界外点数d=0;(2)连续35个点,界外点数d≤1;(3)连续100个点,界外点数d≤2。
二:判异准则SPC的基准是稳态,如若过程出现显著偏离稳态则为异态。
异态出可分为异常好与异常坏两类。
判异准则:(1)点出界就判异;(2)界内点排列不随机判异。
2.1判异准则1一点落在A区以外。
出现该情况可能因素:计算错误、测量误差、原材料不合格、设备故障等。
点排布如下图2-1所示:图2-1 准则1判异图2.2判异准则2出现连续9点落在中心线一侧。
原因:分布的a减小。
点排布如下图2-2所示:图2-2 准则2判异图2.3判异准则3连续6点递增或递减。
产生趋势可能因素:工具逐渐磨损、维修水平逐渐降低、操作人员技能逐渐降低等。
点排布如下图2-3所示:图2-3 准则3判异图2.4判异准则4连续14点中相邻点上下交替。
产生趋势可能因素:轮流使用两台设备、两位人员轮流操作。
点排布如下图2-4所示:图2-4 准则4判异图2.5判异准则5连续3点落在中心线同一侧的B区以外。
产生趋势可能因素:参数u发生了变化。
点排布如下图2-5所示:图2-5准则5判异图2.6判异准则6连续5点中有4点落在中心线同一侧的C区以外。
表明参数u发生了变化。
点排布如下图2-6所示:图2-6准则6判异图2.7判异准则715点在C区中心线上下。
可能原因:①是否应用了假数据,弄虚作假;②是否数据分层不够。
点排布如下图2-7所示:图2-7准则7判异图2.8判异准则88点在中心线两侧,但无一在C区中。
原因:数据分层不够。
点排布如下图2-8所示:图2-8准则8判异图。



SPCSPC(Statistical Process Control,统计过程控制或统计制程控制)目录∙ 1 什么是SPC∙ 2 SPC起源与发展∙ 3 3σ原理简介∙ 4 SPC技术原理∙ 5 SPC控制图及计算∙ 6 SPC控制图(管制图)的实施∙7 SPC控制图(管制图)异常的判断及处理∙8 制程能力指数(参数)CPK∙9 SPC的发展特点∙10 SPC对企业带来的好处什么是SPCSPC即英文“Statistical Process Control”之缩写,意为“统计制程控制” SPC或称统计过程控制。
SPC主要是指应用统计分析技术对生产过程进行实时监控,科学的区分出生产过程中产品质量的随机波动与异常波动,从而对生产过程的异常趋势提出预警,以便生产管理人员及时采取措施,消除异常,恢复过程的稳定,从而达到提高和控制质量的目的。
在生产过程中,产品的加工尺寸的波动是不可避免的。
它是由人、机器、材料、方法和环境等基本因素的波动影响所致。
波动分为两种:正常波动和异常波动。
正常波动是偶然性原因(不可避免因素)造成的。
它对产品质量影响较小,在技术上难以消除,在经济上也不值得消除。
异常波动是由系统原因(异常因素)造成的。
它对产品质量影响很大,但能够采取措施避免和消除。
过程控制的目的就是消除、避免异常波动,使过程处于正常波动状态。
SPC起源与发展1. 1924年休哈特博士在贝尔实验室发明了品质控制图。
2. 1939年休哈特博士与戴明博士合写了《品质观点的统计方法》。
3.二战后美英将品质控制图方法引进制造业,并应用于生产过程。
4. 1950年,戴明到日本演讲,介绍了SQC的技术与观念。
5.SQC是在发生问题后才去解决问题,是一种浪费,所以发展出了SPC。
6.美国汽车制造商福特、通用汽车公司等对SPC很重视,所以SPC得以广泛应用。
7.ISO9000(2000)体系亦注重过程控制和统计技术的应用(如8.1,8.2.3)。

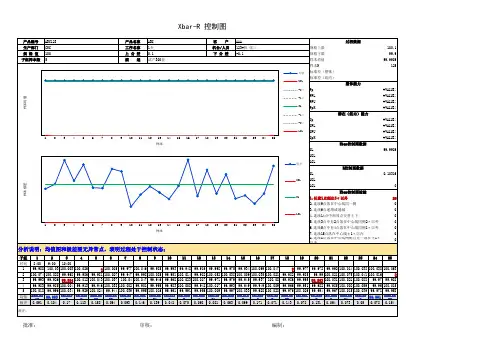


Control Chart管制圖管制圖是一種可用來決定製程可繼續運作或因有問題須解決而必須停止的圖形工具。
管制圖是依時間次序將數據劃圖,會加上3條特別的線。
Centerline(CL)管制中心線:當製程是In-control時,表示製程平均成果(平均值,標準差,良率等等…..) Upper and Lower Control Limits(UCL and LCL)上下管制界限:當製程是In-control時,製程成果的限制範圍管制界限是在中心線上下3個標準差的位置。
Centerline and Control Limits管制中心線和管制界限Centerline管制中心線:是量測值的中值(mean)或平均值,由中心線可知穩定製程的量測值是否接近中心。
Control Limits管制界限:是以中心線上下3個標準差劃出的線。
定義一個穩定製程的量測值出現的範圍規格界限和管制界限的差別Specification(Spec) Limits(規格界限):(1) 根據客戶需求而定義。
(2) 定義一個產品參數的可接受範圍。
(3) 定義何種為可接受產品,何種為不可接受產品。
(4) 用來決定製程的性能。
Control limits(控制界限):(1) 根據實際製程性能的資料計算而來的。
(2) 描述一個穩定製程的性能自然範圍。
(3) 描述自然製程偏差值的量。
(4) 用來決定製程穩定度。
Control Chart Development Procedure(管制圖建立程序):1. 最初的數據收集(Initial data collection)至少收集30個數據,目的是收集足夠數據正確的描述長期變異和檢查參數的穩定性。
PDC所收集的數據亦可用做此用途,但PDC的樣本數頻率須和PCS所使用的相同。
另外,所有新data必須被收集,如同量測計劃中所要求的。
2.管制界限計算(Control Limit Calculation )數據會用做計算管制界限,然後長期使用在管制圖上。
3.建立永久管制圖(Permanent Control Chart Setup )制訂永久管制圖做為長期使用,同時以SPC準則(SPC Rules)決定參數是否超出管制(out of control),亦做為製程更新管制圖的界限之用。
Step1---Initial Data Collection(最初的數據收集)從製程中收集數據,須為一致的方式(即沒有異於平常的製程改變或調整)。
建議數據來自30個獨立的製程作業或批次,以得到充份地正確地製程變異的估計值必須經由量測計劃收集30組數據的原因如下﹕(1)管制界限的計算需要製程變異的估計值,細節不在此課程範圍。
統計理論說明,一個充分正確的製程變異估計值需要至少30組獨立數值。
少於30個數據就沒有非常正確的製程變異估計值。
(2)我們要計算的管制界限來代表製程的真實長期變異,這包括每天來自人、物料設備等變異的波動。
如果數據收集自較短的期間,此數據可能無法包括該製程所有長期變異的來源。
2. 變換(Transform)數據以得到常態分配。
註:有數個方法適用於難以取得30批或30組數據的情況,請參考ISM 教材。
Step2---Control Limit Calculation (控制界限的計算)a) 依時間依序劃趨勢圖(Trend Chart),量測計劃的結果以單點表示在趨勢圖上。
b) 檢查“noisy data ”,(例 outliers ,非常態(non-Normality)和 Autocorrelation ) 對數據執行必要的調整和更正:1. 移除所有的Outliers (無法解釋原因的outlier ,不能移除) 3. 注意任何顯著的Autocorrelation 。
(Note:依ISM 教材上的工具和步驟,須測和處理Noisy data ,同時用特別 的管制界限計算方法在 Autocorrelation 數據上。
)c) 計算管制界限並將之劃在趨勢圖上,此時趨勢圖就轉變成管制圖。
d) 檢查管制圖的不穩定性 1. 任何點在管制界限外。
2. 任何非隨意( non-random ) 的點。
e) 假如管制圖上有任何超出管制(out of control)的點,重覆下列步驟: 1. 移除圖上超出管制的點2. 重新計算管制界線,不含超出管制的點。
3. 重劃管制圖(資料和新的管制界限)。
4. 重覆上述步驟直到沒有任何點在管制界限外。
(Note:任何時候資料若少於25筆時,再收集更多資料。
控制界限用至少25 筆讀取值來計算是很重要的)˙Control Limit Formulas (管制界限公式)有許多方法可計算管制界限,在某些情況有些較好,在此課程中使用的管制 界限計算方法在大部份或所有情況下都可以用的很好。
稱為Moving Range (MR) Method 。
˙N = 用於計算管制界限的批數˙X i = 第i 個管制點( i=1,2……,N )。
請注意,X i 可為平均值,標準差,範圍, 良率或缺點率。
MR Method 可用於計算任何管制圖的管制界限。
˙MR i =第i 個管制點的移動距離,MR i =│X i - X i+1│。
(注意,共有N-1個移動距離Moving Ranges)。
˙X = 管制點的平均值 x x Nii N==∑1˙MR = 平均移動距離 M RM RN ii N =−=−∑111管制界限計算如下:註:―MR是1.128σ的估計值,所以2.66MR是3σ的估計值。
―關於管制界限計算方式的更詳細說明請參考ISM教材。
EXAMPLE:以下數據表包含N=30批產品的鍍層厚度平均值和標準差(抽樣數=5片/批) Lot Lot Lot Lot Mean Lot Std. Dev.Number Mean Std. Dev. Moving Range Moving Range1 152.27 0.40 0.15 0.012 152.12 0.41 0.38 0.073 151.74 0.48 0.70 0.034 152.44 0.51 0.58 0.025 153.02 0.53 0.44 0.086 152.58 0.45 0.26 0.027 152.32 0.47 0.54 0.028 151.78 0.45 0.00 0.039 151.78 0.42 0.51 0.0110 152.29 0.43 0.39 0.0611 152.68 0.49 0.87 0.0412 151.81 0.45 0.92 0.0713 152.73 0.52 0.24 0.1214 152.97 0.40 1.14 0.0315 151.83 0.43 0.62 0.0416 152.45 0.47 0.17 0.0217 152.28 0.49 0.11 0.0118 152.39 0.50 1.04 0.0819 153.43 0.42 1.05 0.0220 152.38 0.44 0.40 0.0121 151.98 0.43 0.52 0.0122 152.50 0.44 0.45 0.1023 152.95 0.54 0.02 0.0524 152.97 0.49 0.36 0.0325 152.61 0.46 0.23 0.0226 152.84 0.48 1.01 0.0527 151.83 0.53 1.37 0.0628 153.20 0.47 0.57 0.0129 152.63 0.48 0.23 0.0230 152.86 0.46 --- ---152.455 0.465 0.527 0.039 Mean1.劃趨勢圖:選擇Chart 下之over plot ,Lot number 設為X ,Lot mean 設為Y ,按執行(確認) 2.測驗Autocorrelation打開Autocorr.jmp 檔案,將檔案plate.jmp 之Lot mean 複製到Autocorr.jmp 內 之data 欄,檢查p-value 大於0.05表示沒有Autocorrelation 。
Check for Noisy Data(Lot Means)Trend ChartNormal Probability plot152.0152.5檢查批平均值的Noisy data :1.檢查outlier ,打開outlier.jmp ,將檔案plate.jmp 之Lot mean 複製到outlier.jmp 內之data 欄,檢查outlier 欄,Yes 表示該點為outlier 。
2.檢查是非常態分配 選擇Analyte註:―測驗autocorrelation 可用JMP 模板檔案Autocorr.jmp 來執行 ―測驗outlier 可用JMP 模板檔案outlier.jmp 來執行 Check for Noisy Data (Lot Standard Deviations):T rend Chart: Normal Probability Plot:Test for Autocorrelation:Test for Normality:r1 t p-value W Prob<W 0.130 0.694 0.4931 0.966758 0.5014Test for Outliers:Lot Data M Outlier? Lot Data M Outlier? Lot Data M Outlier? 1 0.40 -2.6 No 11 0.49 1.0 No 21 0.43 -1.8 No 2 0.41 -2.2 No 12 0.45 -0.6 No 22 0.44 -1.0 No 3 0.48 0.6 No 13 0.52 2.2 No 23 0.54 3.0 No 4 0.51 1.8 No 14 0.40 -2.6 No 24 0.49 1.0 No 5 0.53 2.6 No 15 0.43 -1.4 No 25 0.46-0.2 No 6 0.45 -0.6 No 16 0.47 0.2 No 26 0.48 0.6 No 7 0.47 0.2 No 17 0.49 1.0 No 27 0.53 2.6 No 8 0.45 -0.6 No 18 0.50 1.4 No 28 0.47 0.2 No 9 0.42 -1.8 No 19 0.42 -1.8 No 29 0.48 0.6 No 10 0.43 -1.4 No 20 0.44 -1.0 No 30 0.46 -0.2 NoControl Limit Calculations:• X-Bar Chart:x =152455. and MR x ().=0527C L 152.455U C LL C L x x ===153.855151.055• S Chart:s =0465. and MR s ().=0039C L 0.465U C L.569L C L.360s s s ===00 X-Bar Chart:S Chart:Step3---Permanent Control Chart Setup(建立永久管制圖)˙Control Chart.使用計算出來最後一組控制界限來建立一個參數的永久管制圖˙Control Limit Update Procedure管制界限更新步驟建立重新計算和更新管制界限的步驟。