第(11)章如何选取样本.

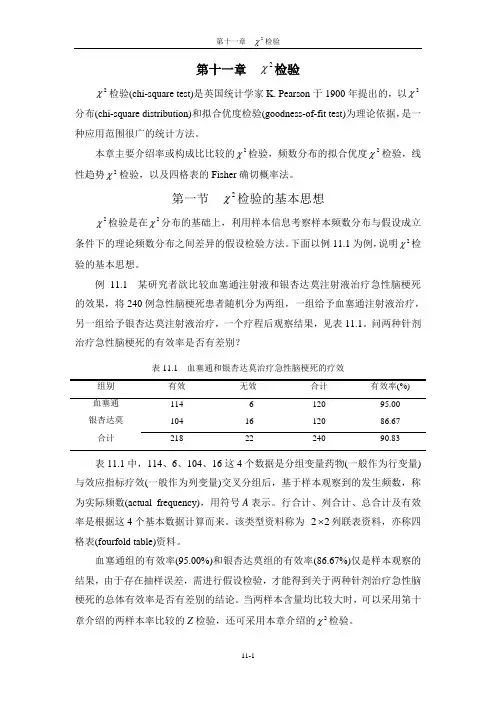
第十一章2χ检验2χ检验(chi-square test)是英国统计学家K. Pearson于1900年提出的，以2χ分布(chi-square distribution)和拟合优度检验(goodness-of-fit test)为理论依据，是一种应用范围很广的统计方法。

本章主要介绍率或构成比比较的2χ检验，频数分布的拟合优度2χ检验，线χ检验，以及四格表的Fisher确切概率法。

性趋势2第一节2χ检验的基本思想2χ检验是在2χ分布的基础上，利用样本信息考察样本频数分布与假设成立条件下的理论频数分布之间差异的假设检验方法。

下面以例11.1为例，说明2χ检验的基本思想。

例11.1 某研究者欲比较血塞通注射液和银杏达莫注射液治疗急性脑梗死的效果，将240例急性脑梗死患者随机分为两组，一组给予血塞通注射液治疗，另一组给予银杏达莫注射液治疗，一个疗程后观察结果，见表11.1。

问两种针剂治疗急性脑梗死的有效率是否有差别？表11.1 血塞通和银杏达莫治疗急性脑梗死的疗效血塞通114 6 120 95.00银杏达莫104 16 120 86.67合计218 22 240 90.83表11.1中，114、6、104、16这4个数据是分组变量药物(一般作为行变量)与效应指标疗效(一般作为列变量)交叉分组后，基于样本观察到的发生频数，称为实际频数(actual frequency)，用符号A表示。

行合计、列合计、总合计及有效率是根据这4个基本数据计算而来。

该类型资料称为22⨯列联表资料，亦称四格表(fourfold table)资料。

血塞通组的有效率(95.00%)和银杏达莫组的有效率(86.67%)仅是样本观察的结果，由于存在抽样误差，需进行假设检验，才能得到关于两种针剂治疗急性脑梗死的总体有效率是否有差别的结论。

当两样本含量均比较大时，可以采用第十章介绍的两样本率比较的Z检验，还可采用本章介绍的2χ检验。

一、对总体建立假设例11.1的无效假设为012:H ππ=，即两种针剂治疗急性脑梗死的有效率相同。

如何进行有效的调查研究与样本选择调查研究是社会科学中广泛使用的一种研究方法，通过收集、分析和解释数据，来获取对特定问题的深入理解。

而一个有效的调查研究必须依赖于合适的样本选择和严谨的调查方法。

本文将介绍如何进行有效的调查研究与样本选择。

首先，样本选择是调查研究设计中至关重要的一步。

一个好的样本应当具有代表性，即能够准确反映目标群体的特征和态度。

为了实现代表性，我们可以采用随机抽样的方法。

随机抽样是指每个人都有相等机会被选中的抽样方法，可以减小样本的偏倚性。

常用的随机抽样方法有简单随机抽样、系统抽样、分层抽样等。

选择适当的抽样方法取决于研究的具体目的和资源预算。

其次，调查研究中收集数据的方法也需慎重选择。

调查方法可以是面对面访谈、电话访谈、邮寄调查或在线调查等。

不同的调查方法适用于不同的研究对象和研究目的。

面对面访谈有利于获取详细和全面的信息，但成本较高且可能引起被访者不真实回答的问题。

电话访谈则成本相对较低，但可能受到抽样偏差和拒绝参与的限制。

邮寄调查对于大规模样本的研究有优势，但需要注意回收率较低的问题。

在线调查则成本较低且方便参与者，但仍面临抽样偏差和样本不够代表性的问题。

根据研究的具体需求和资源条件，我们需要综合考虑选择合适的调查方法。

在实施调查过程中，确保数据的准确性和可靠性是至关重要的。

一些常见的数据收集问题包括问卷设计、访谈技巧和数据录入。

问卷设计时应注意问题的准确性、明确性和序列性，避免提问歧义或导致主观性答案的问题。

访谈人员应接受专业训练以获得高质量的数据。

数据录入过程中应注意对数据进行验证和清理，以确保数据的准确性和一致性。

最后，数据分析是一个关键的环节。

根据研究问题的性质和调查方法的特点，我们可以采用不同的数据分析方法。

对于定性分析，可以通过编码和归纳的方式对数据进行分析。

对于定量分析，我们可以使用统计软件进行描述性统计和推论统计分析。

需要注意的是，数据分析的结果需要客观、准确地反映研究问题，避免主观偏见和不恰当的解释。

工作总结医学研究中的样本收集与处理在医学研究中，样本的收集与处理是非常重要的环节。

它涉及到研究结果的准确性和可靠性。

本文将从样本收集的主要步骤、样本处理的方法以及注意事项等方面进行总结。

一、样本收集1. 研究对象的选择在进行医学研究时，首先需要明确研究对象。

根据研究的目的和假设，选择合适的研究对象，如人体组织、血液、尿液、细胞等。

同时，要确定样本的数量和质量要求。

2. 规范化的操作步骤在样本收集过程中，需要严格按照规范化的操作步骤进行。

这包括消毒、穿戴无菌手套和口罩，避免污染样本。

3. 采集合适的样本量样本的数量要根据研究的需求和统计学原理进行确定。

过少的样本容易导致研究结果不够准确，而过多的样本则会增加工作量。

在样本采集过程中，要确保获得足够的样本量。

4. 样本记录和标识在收集样本的同时，要记录详细的信息，如样本编号、采集时间、采集者等。

同时，每个样本都需要进行标识，以便后续的处理与分析。

二、样本处理1. 样本保存与储存在医学研究中，样本的保存非常重要。

不同的样本要采用不同的保存方式，如低温冷冻、冷藏、干燥等。

在进行样本储存时，要确保样本的完整性和稳定性。

2. 样本预处理有时，样本需要经过预处理才能进行进一步的分析。

例如，血液样本可能需要离心来分离血清或血细胞。

在进行样本预处理时，要确保操作准确，避免对样本造成不必要的损伤。

3. 数据采集与分析样本处理后，需要进行数据采集与分析。

这包括对样本的性质、成分、浓度等进行测量和统计。

根据需要，可以采用各种各样的实验技术和仪器来获取所需数据。

三、注意事项1. 符合伦理要求在进行医学研究时，样本的收集和处理要符合伦理要求，尊重研究对象的权益。

研究项目需经过伦理委员会的审核和批准。

2. 严格控制实验条件样本的收集与处理过程中，实验条件的严密控制是确保结果准确的关键。

如操作环境的清洁、温度的控制、时间的准确记录等。

3. 重复实验与验证结果为了确保结果的可靠性，对于重要的实验结果，需进行重复实验与验证。

© 陈强，2015年，《计量经济学及Stata应用》，高等教育出版社。

第11章二值选择模型11.1 二值选择模型如果被解释变量y离散，称为“离散选择模型”(discrete choice model)或“定性反应模型”(qualitative response model)。

最常见的离散选择模型是二值选择行为(binary choices)。

比如：考研或不考研；就业或待业；买房或不买房；买保险或不买保险；贷款申请被批准或拒绝；出国或不出国；回国或不回12国；战争或和平；生或死。

假设个体只有两种选择，比如1y =(考研)或0y =(不考研)。

最简单的建模方法为“线性概率模型”(Linear Probability Model ，LPM)：1122(1,,)i i i K iK i i i y x x x i n βββεε'=+=+= +++x β (11.1)其中，解释变量12()i i i iK x x x '≡ x ，而参数12()K βββ'≡ β。

LPM 的优点是，计算方便，容易得到边际效应(即回归系数)。

3LPM 的缺点是，虽然y 的取值非0即1，但根据线性概率模型所作的预测值却可能出现ˆ1y>或ˆ0y <的不现实情形。

图11.1 线性概率模型4为使y 的预测值介于[0,1]之间，在给定x 的情况下，考虑y 的两点分布概率：P(1|)(,)P(0|)1(,)y F y F ==⎧⎨==-⎩x x x x ββ (11.2)函数(,)F x β称为“连接函数”(link function) ，因为它将x 与y 连接起来。

y 的取值要么为0，要么为1，故y 肯定服从两点分布。

连接函数的选择具有一定灵活性。

通过选择合适的连接函数(,)F x β(比如，某随机变量的累积分布函数)，可保证ˆ01y≤≤，并将ˆy 理解为“1y =”发生的概率，因为5E(|)1P(1|)0P(0|)P(1|)y y y y =⋅=+⋅===x x x x (11.3)如果(,)F x β为标准正态的累积分布函数，则P(1|)(,)()()y F t dt φ'-∞'===Φ≡⎰x x x x βββ (11.4)()φ⋅与()Φ⋅分别为标准正态的密度与累积分布函数；此模型称为“Probit ”。

区间估计的基本概念前面介绍了参数的点估计，讨论了估计量的优良性准则，给出了寻求估计量最常用的矩估计法和最大似然估计法.参数的点估计是用一个确定的值去估计未知参数，看似精确，实际上把握不大，没有给出误差范围，为了使估计的结论更可信，需要引入区间估计.Neyman(1894–1981)引例在估计湖中鱼数的问题中，若根据一个实际样本，得到鱼数N的最大似然估计为1000条.实际上，N的真值可能大于1000，也可能小于1000.为此，希望确定一个区间来估计参数真值并且满足：1.能以比较高的可靠程度相信它包含参数真值.“可靠程度”是用概率来度量的.2.区间估计的精度要高.可靠度：越大越好估计你的年龄八成在21－28岁之间区间：越小越好被估参数可靠度范围、区间一、置信区间的定义（Confidence Interval ）对于任意θ∈Θ，满足设总体X 的分布函数F (x ,θ)含有一个未知参数θ，θ∈Θ,对于给定常数α(0<α<1)，若由抽自X 的样本X 1,X 2,…,X n 确定两个统计量112212ˆˆ{(,,,)(,,,)}1n n P X X X X X X θθθα<<≥-112ˆ(,,,)nX X X θ212ˆ(,,,)nX X X θ和则称随机区间是θ的置信水平为1−α的置信区间.12ˆˆ(,)θθ和分别称为置信下限和置信上限.1ˆθ2ˆθ（1）当X 连续时，对于给定的α，可以求出置信区间满足此时，找区间使得至少为1−α，且尽可能接近1−α.12ˆˆ(,)θθ112212ˆˆ{(,,,)(,,,)}1nnP X X X X X X θθθα<<=-12ˆˆ(,)θθ112212ˆˆ{(,,,)(,,,)}1n n P X X X X X X θθθα<<=-12ˆˆ()P θθθ<<（2）当X 离散时，对于给定的α，常常找不到区间满足12ˆˆ(,)θθ说明：（2）估计的精度要尽可能高. 如要求区间长度尽可能短，或者能体现该要求的其他准则.（1）要求θ以很大的可能被包含在区间内，即概率尽可能的大.可靠度与精度是一对矛盾，一般是在保证可靠度的条件下尽可能提高精度.12ˆˆ()P θθθ<<12ˆˆ(,)θθ21ˆˆθθ-（3）对于样本(X 1,X 2,…,X n )112212ˆˆ((,,,),(,,,))n n X X X X X X θθ以1−α的概率保证其包含未知参数的真值.随机区间112212ˆˆ{(,,,)(,,,)}1n n P X X X X X X θθθα<<=-即有：（4）对于样本观测值(x 1,x 2,…,x n )可以理解为：该常数区间包含未知参数真值的可信程度为1−α.112212ˆˆ((,,,),(,,,))n n x x x x x x θθ常数区间只有两个结果，包含θ和不包含θ.此时，不能说：112212ˆˆ{(,,,)(,,,)}1n n P x x x x x x θθθα<<=-没有随机变量，自然不能谈概率如：取1−α=0.95.若反复抽样100次，样本观测值为112212ˆˆ{(,,,)(,,,)}1n n P X X X X X X θθθα<<=-1121ˆˆ((,,),(,,))i i i in n x x x x θθ于是在100个常数区间中，包含参数真值的区间大约为95个，不包含真值的区间大约为5个.12,,,ii i nx x x1,2,,100i =对应的常数区间为1,2,,100i =对一个具体的区间而言，它可能包含θ，也可能不包含θ，包含θ的可信度为95%.1121ˆˆ((,,),(,,))i i i i nnx x x x θθ二、构造置信区间的方法枢轴量法1.寻求一个样本X 1,X 2,…,X n 和θ的函数W =W (X 1,X 2,…,X n ;θ)，使得W 的分布不依赖于θ和其他未知参数，称具有这种性质的函数W 为枢轴量（Pivotal quantity ）.3.若由不等式a <W (X 1,X 2,…,X n ;θ)<b 得到与之等价的θ的不等式2.对于给定的置信水平1−α，定出两个常数a 和b ，使得P {a <W (X 1,X 2,…,X n ;θ)<b }=1−α112212ˆˆ(,,,)(,,,)n n X X X X X X θθθ<<即有P {a <W (X 1, X 2,…, X n ;θ)<b }关键：1.枢轴量W (X 1, X 2,…, X n ;θ)的构造2.两个常数a ,b 的确定一般从θ的一个良好的点估计出发构造，比如MLE因此，是θ的一个置信水平为1−α的置信区间.112212ˆˆ{(,,,)(,,,)}1n n P X X X X X X θθθα=<<=-12ˆˆ(,)θθf (w )ababab1−α1−α1−α希望置信区间长度尽可能短.对于任意两个数a 和b ，只要使得f (w )下方的面积为1−α，就能确定一个1−α的置信区间.f(w)abab ab1−α1−α1−α当W 的密度函数单峰且对称时，如：N (0,1),t 分布等，当a =−b 时求得的置信区间的长度最短.如：b =z α/2或t α/2(n )当W 的密度函数不对称时，如χ2分布，F 分布，习惯上仍取对称的分位点来计算未知参数的置信区间.χ21−αα/2α/222()n αχ21-2()n αχ单个正态总体参数的区间估计一、单个正态总体的情形X 1, X 2,…, X n 为来自正态总体N (μ,σ2)的样本，置信水平1−α.样本均值样本方差11nii X X n ==∑2211()1nii S X X n ==--∑0-4-3-2-1012340.050.10.150.20.250.30.350.4是枢轴量W 是样本和待估参数的函数，其分布为N (0,1)，完全已知由于是μ的MLE ，且是无偏估计，由抽样分布定理知X ~(0,1)X W N nμσ-=1.均值μ的置信区间（方差σ2已知情形）单峰对称-4-3-2-1012340.050.10.150.20.250.30.350.4即等价变形为选择两个常数b =−a =z α/222{}1X P z z nααμασ--<<=-22{}1P X z X z nnαασσμα-<<+=-1−αα/2α/2z α/2−z α/2简记为因此，参数μ的一个置信水平为1−α的置信区间为22(,)X z X z nnαασσ-+2()X z nασ±置信区间的长度为22n l z nασ=说明：2.置信区间的中心是样本均值；4.样本容量n 越大，置信区间越短，精度越高；1.l n 越小，置信区间提供的信息越精确；5.σ越大，则l n 越大，精度越低.因为方差越大，随机影响越大，精度越低.3.置信水平1−α越大，则z α/2越大.因此，置信区间长度越长，精度越低；22n l z nασ=22(,)X z X z nnαασσ-+2.均值μ的置信区间（方差σ2未知情形）想法：用样本标准差S 代替总体标准差σ.是枢轴量包含了未知未知参数σ，~(0,1)X W N nμσ-=此时，因此不能作为枢轴量.~(1)X T t n Snμ-=-由抽样分布理论知：使即枢轴量~(1)X T t n Snμ-=-22((1)(1))1X P t n t n Snααμα---<<-=-22{(1)(1)}1P t n T t n ααα--<<-=-选择两个常数b =−a =t α/2 (n -1)等价于因此，方差σ2未知情形下均值μ的一个置信水平为1−α的置信区间为22{(1)(1)}1S S P X t n X t n nnααμα--<<+-=-22((1),(1))X t n X t n nnαα--+-例1.现从中一大批糖果中随机取16袋，称得重量（以克记）如下：506508 499 503 504 510 497 512 514 505 493 496 506 502 509 496设每袋糖果的重量近似服从正态分布. 试求总体均值μ的置信水平为0.95的置信区间.解：这是单总体方差未知，总体均值的区间估计问题.均值μ的置信水平1−α的置信区间为22((1),(1))x t n x t n nnαα--+-根据给出的数据，算得这里10.95,16n α-==/20.025(1)(15) 2.1315t n t α-==503.75, 6.2022x s ==因此，μ的一个置信水平为0.95的置信区间为6.20226.2022(503.75 2.1315,503.75 2.1315)1616(500.4,507.1)-⨯+⨯=此区间包含μ的真值的可信度为95%.22((1),(1))x t n x t n nnαα--+-3.方差σ2的置信区间（均值μ未知）σ2的常用点估计为S 2，且是无偏估计。

第十一章 非参数检验前面有关章节讨论的参数检验都要求总体服从一定的分布，对总体参数的检验是建立在这种分布基础上的。

例如，两样本平均数比较的t 检验和多个样本平均数比较的F 检验，都要求总体服从正态分布，推断两个或多个总体平均数是否相等。

本章引入另一类检验——非参数检验（non-parametric test ）。

非参数检验是一种与总体分布状况无关的检验方法，它不依赖于总体分布的形式，应用时可以不考虑被研究的对象为何种分布以及分布是否已知。

非参数检验主要是利用样本数据之间的大小比较及大小顺序，对两个或多个样本所属总体是否相同进行检验，而不对总体分布的参数如平均数、标准差等进行统计推断。

当样本观测值的总体分布类型未知或知之甚少，无法肯定其性质，特别是观测值明显偏离正态分布，不具备参数检验的应用条件时，常用非参数检验。

非参数检验具有计算简便、直观，易于掌握，检验速度较快等优点。

非参数检验法从实质上讲，只是检验总体分布的位置（中位数）是否相同，所以对于总体分布已知的样本也可以采用非参数检验法，但是由于它不能充分利用样本内所有的数量信息，检验的效率一般要低于参数检验方法。

例如，非配对资料的秩和检验，其效率为t 检验的86.4%，就是说以相同概率判断出差异显著，t 检验所需的样本个数要少13.6%。

非参数检验内容很多，本章只介绍常用的符号检验（sign test ），秩和检验（rank-sum test ）和等级相关分析（rank correlation analysis ）三种。

第一节 符号检验一、配对资料的符号检验（一）配对资料符号检验的意义 配对资料符号检验是根据样本各对数据之差的正负符号多少来检验两个总体分布位置的异同，而不去考虑差值的大小。

每对数据之差为正值用“+”表示，负值用“－”表示。

可以设想如果两个总体分布位置相同，则正或负出现的次数应该相等。

若不完全相等，至少不应相差过大，否则超过一定的临界值就认为两个样本所来自的两个总体差异显著，分布的位置不同。

样本量的确定范文1.研究目的和研究问题：确定样本量前，首先要明确研究目的和研究问题。

不同的研究目的和问题需要不同样本量的支持。

例如，如果是进行描述性研究，样本量可以较小；如果是进行推断性研究，样本量则需要更大。

2.效应大小：效应大小是指研究中所关注的变量之间的差异或相关性的大小。

一般来说，效应越大，需要的样本量就越小。

3.α水平和β水平：α水平是指犯第一类错误的概率，即在实际上无差异的情况下，错误地拒绝了零假设。

β水平是指犯第二类错误的概率，即在实际上存在差异的情况下，错误地接受了零假设。

一般来说，α水平设定为0.05，β水平设定为0.2、样本量的确定需要考虑α水平和β水平的要求。

4.效应检验的统计方法：样本量的确定还与所采用的统计方法有关。

不同的统计方法要求不同的样本量。

例如，如果采用参数检验方法，需要的样本量一般较多；如果采用非参数检验方法，需要的样本量可以相对较少。

在确定样本量时，通常可以通过统计学中的样本量计算方法来进行估算。

常用的样本量计算方法包括：1.Z检验的样本量计算方法：用于比较两个独立样本的平均值差异。

2.t检验的样本量计算方法：用于比较两个相关样本或配对样本的平均值差异。

3.方差分析的样本量计算方法：用于比较多个样本的平均值差异。

4.相关分析的样本量计算方法：用于评估两个变量之间的相关性。

以上提到的方法都可以在各种统计软件中找到相应的样本量计算工具，根据研究设计和数据分析方法进行计算。

最后，还需要注意的是，样本量的确定是一种平衡考虑。

过小的样本量可能导致统计检验结果不可靠，过大的样本量则会浪费资源和时间。

因此，在确定样本量时，需要综合考虑以上多个因素，并在可行的范围内选择一个合适的样本量。