第三章_投入产出核算习题_答案

单选：1. 抽入产出分析是由经济学家（　B ）在20世纪30年代提出的一种经济数量分析方法。

A． 瓦尔拉斯 B.列昂惕夫 C.萨缪尔森 D.索洛2. 下列说法错误的是（ D ）A投入是指经济活动过程中的各种消耗及其来源B产出是指经济活动的成果及其使用去向C投入产出表按照计量单位的不同分为价值型和实物型D投入产出表的平衡关系式：中间产品+中间投入=总产品3 .下面哪个不是投入产出的基本假定（ D ）A同质性假定 B比例性假定 C相加性假定 D消耗系数绝对稳定性假定4. 投入产出按资料范围可分为宏观模型和微观模型两大类，下列不属于宏观模型的是（ C ）A国家模型 B地区模型 C 企业模型 D部门模型5. 下列不属于经济要素的是（ A ）A企业 B原料 C价格 D劳动力6. 下列说法正确的是（ B ）A马克思把国民生产划分为生产资料和生活资料量大部类的再生产理论B费兰索。

魁奈提出“全部均衡理论”，把各部门的投入和产出联系起来考察C物质生产部门指那些能创造物质产品以及直接实现产品价值的部门。

D投入产出模型是指用数学形式体现投入产出表所反映的经济内容的线性代数方程组7.利用投入产出表，可以精确地计算出整个社会产品中，两大部类各自的总量及其价值构成。

其具体计算过程分为四个步骤：（B ）（a） 计算第二部类产品的价值构成（b） 计算第一部类和第二部类的总量（c） 计算各部门的部门消耗系数.劳动报酬系数和社会纯收入系数（d） 计算第一部类产品的价值构成它们的正确排序为：A.abcdB.bcadC.cbadD.abdc8.下列哪个选项不是投入产出模型在宏观经济分析中的应用: (D )A.分析农业. 轻工业. 重工业的比例关系B.分析两大部类的比例关系C.分析各部门之间的比例关系D.分析国民经济大型项目建设与整个国民经济发展之间的平衡9.投入产出模型在制定国民经济计划中的作用为：（ B ）（a） 为从社会最终产品出制定国民经济计划，提供了一种科学方法（b） 能够成为加强国民经济综合平衡的重要工具A.（a）B.(a)(b)C.(b)D.一个都不是n n n10.∑(vj+mj)／∑ ∑Xij是分析 ：（ A ）j=1 i=1 j=1A. 国民收入与物资消耗的比例B. 社会总产品与社会化成本的比例C. 消费数量与劳动报酬的比例D. 消费数量与社会总成本的比例11.下列不属于从最终产品出发制定国家计划的过程的是：（ B ）A. 确定计划期所需要达到的消费总量B. 根据报告期生产的增长情况确定投资C. 利用公式计算计划期各部门的总产量D．确定计划期的直接消费系数12.大量的经验表明，价值形态的投入产出表一般为（B）个部门左右A、50B、100C、150D、20013.实物投入产出表一般为（D）个部门左右是较为合适的。

投入产出法农产品进项税计算例题摘要：1.投入产出法计算农产品进项税的概念和核心2.投入产出法计算农产品进项税的步骤和公式3.投入产出法计算农产品进项税的例题及解答正文：一、投入产出法计算农产品进项税的概念和核心投入产出法是一种计算农产品进项税的方法，其核心是单耗水平的高低。

单耗水平是指生产单位数量货物所需耗用的农产品数量。

投入产出法参照国家标准、行业标准（包括行业公认标准和行业平均耗用值）来确定销售单位数量货物耗用外购农产品的数量，即农产品单耗数量。

二、投入产出法计算农产品进项税的步骤和公式1.确定农产品单耗数量：参照国家标准、行业标准来确定销售单位数量货物耗用外购农产品的数量。

2.计算当期允许抵扣农产品增值税进项税额：公式为：当期允许抵扣农产品增值税进项税额= 当期农产品耗用数量× 农产品平均购买单价× 扣除率/ (1 + 扣除率)。

其中，扣除率是农产品增值税进项税额扣除率，当期农产品耗用数量是指当期用于生产货物的农产品数量，农产品平均购买单价是指当期购进的农产品的平均单价（含税）。

三、投入产出法计算农产品进项税的例题及解答例题：某企业购进农产品，当期用于生产货物的数量为1000 吨，农产品平均购买单价为10000 元/吨，扣除率为10%，求当期允许抵扣农产品增值税进项税额。

解答：1.确定农产品单耗数量：假设该企业生产1 吨货物需要耗用2 吨农产品，则当期农产品耗用数量为1000 吨× 2 = 2000 吨。

2.计算当期允许抵扣农产品增值税进项税额：当期允许抵扣农产品增值税进项税额= 2000 吨× 10000元/吨× 10% / (1 + 10%) = 18181.82 元。

第一章总论一、简答题1．什么是国民经济核算？国民经济核算的功能有哪些？它为何能够赢得来自经济学界和宏观经济管理部门的如此重视？2．何谓常住单位和非常住单位？区分它们的简要原则是什么？试举例说明。

3．如何区分国民经济核算中的机构部门和产业部门？列举现实生活中的经济单位，分别将其归入所属机构部门和所属产业部门，并比较机构部门分类与产业部门分类在国民经济核算及其分析中的作用。

二、单项选择题1．国民经济核算是对_____所进行的系统定量描述。

A. 物质生产活动B. 非物质生产活动C. 社会经济活动D. 国民经济活动总体2．下列属于我国常住单位的是_______。

A. 外商投资企业B. 外国领事馆C. 季节性来华务工人员D. 外国机构在中国的临时办事处3．_____反映了生产过程中各产业相互之间的生产与使用关系，对产业部门之间的货物服务流量做了详细的描述。

A. 国民收入与生产核算B. 资金流量核算C. 投入产出核算D. 资产负债核算答案：1.D 2.A 3.C三、多项选择题（答案有两项或两项以上）1.国民经济核算的主要特点是_____。

A．以宏观经济理论为基础B．以货币作为统一的计量单位C．引入工商企业会计的复式记账原理D．以一国经济总体为核算对象E．提供一套完整的数据体系2.国民经济核算与工商企业会计的关系表现为________。

A．国民经济核算运用了工商企业会计的账户形式B．两者在核算方法及核算原则上一致C．国民经济核算数据主要来源于工商企业会计核算D．两者的核算对象和目的不同E．国民经济核算引入了工商企业会计的复式记账法3.下列企业和单位中，属于中国经济领土范围内的常住单位的是_____。

A．日本驻华大使馆B. 中国驻洛杉矶领事馆C. 正在利比亚执行为期三个月维和任务的中国工兵小分队D. 深圳的一家中韩合资网络游戏开发公司E. 海尔集团在美国新收购的一家冰箱生产企业.答案：1.ABCDE 2.ACDE 3.BCD四、判断题1．国民经济核算的目的不仅是为了计算若干核心指标，而是要描述国民经济运行过程方方面面的全景，提供的是一个完整的数据体系。

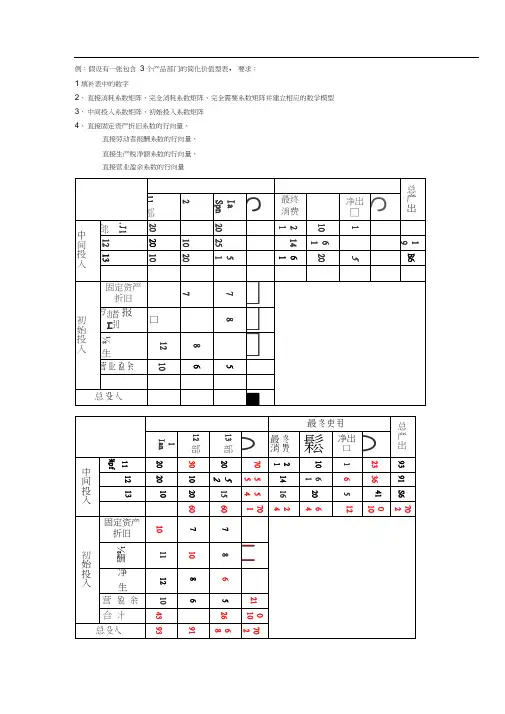
例：假设有一张包含3个产品部门的简化价值型表，要求：1填补表中的数字2、直接消耗系数矩阵、完全消耗系数矩阵、完全需要系数矩阵并建立相应的数学模型3、中间投入系数矩阵、初始投入系数矩阵4、直接固定资产折旧系数的行向量、直接劳动者报酬系数的行向量、直接生产税净额系数的行向量、直接营业盈余系数的行向量建立行模型：Y=(I-A)X2. 直接消耗系数矩阵:<0.5803 0.7614 0.7132、 B = (I-A)'i -I =04918 0.4674 0.6552033670.489804786；中间投入系数矩阵:(3Σ⅛O O4 =O ⅛¾2J=IOOOj=∣)<02151+02151+0.1075 OO——O0.3297+ OJ 099+0.2198 OOO 0.2326 + 0.2907 + 0.1744)<0.5376OO ) O0.6593O< OO0.6977J<20 93 20 93 103091 109\ 20 9? 20、 86 25 86 15 r0.2151 =0.2151 .0.1075 032970」099 021980.2326、 02907 0」744丿< 1.5803 07614 0.7132、 B + I = {I-A)~' =0.491814674 0.6552∖(λ33670.4898 14786)9386 J完全需求系数矩阵:完全消耗系数矩阵:<0.7849 03297 02326、= 0.21510.8901 0.2907』丿∖0.1075 0,21980.8256 丿建宜列模璃N=U -心X©46240 0 )=0 03407 0< 00.3023丿生3.价值模型的主要系数直接固定资产折旧系数:丿元素：= d* / JV Z ( / = 1,2，冲向量：直接劳动者报酬系数:丿丿素： =PjXQ = 1,2,- i ΛT)向量：=(EMCi v2…-U Vtt )直接生产税净额和营业盈余系数： 元素： J -Z -\小、向量： f4. Wl^l 定资产折IH 条数的行向呈:直接劳动者报酬系数的行向量：/ 1 11 A Q \A l = — — — =ι(λll83 0.1099 0.0930) (93 91 86丿'J直接生产税净额系数的行向量：(12 Q 6、A = - — — = (OJ 290 0.0879 0069刘 (93 91 86 丿*7也L 2?<93 9? 86；= (0.10750.0769 0.0814)直接营业盈余系数的行向量:第五章出产 1 2门 部 13 费 消 累积中间投入 本地生产 11 6 3 80O 8 8 1 20 8 20 76 O 4029015D 12 3 68 O 38O 8 .13 T O40 1 12078 272 O 5 3OO 60外地输入1 4 40 O 20 8 8 272 12 50 So20 10 20 30 180 3 SrO40 O 1- 10 30 4090 初始投入酬报 者 劳O 6 1 10 2O 15□□□O S 10 2 O 15入投⅛Oo 4o oO 601•本地区产品的直接消耗系数矩阵和完全消耗系数矩阵 2. 外地输入产品的直接消耗系数矩阵和完全消耗系数矩阵3. 根据报告期地区产品的消耗结构与初始投入结构，在输出不变的情况下，若计划期本地区 3个部门的最终产品需求量为224亿元、400亿元、350亿元时，试求出此时(1) 计划期地区各部门产品的总产出(2) 计划期地区投入产出表的第I 象限流量矩阵 (3) 计划期地区投入产出表的第川象限流量矩阵1 •本地区产品的直接消耗系数矩阵为=36400 90 40080 WO O 200IOO O1400 150 600 1200.09 0.08 0 0.2250.2 025 00J402IOOO 60() 6 91^=(Olo75 00659 0'05δ,)1 •本地区产品的完全消耗系数矩阵为:■ 0.91-0.08 0・-I^1 0 0' B d= [l-A dY-I =-0.225 0.8 -0.25 — 0 1 0.00」40.20 ■ 0 I —0.092 0.H5 0.0469 1.3086 -0.7328 3.0842•外地输入产品的直接消耗系数矩阵为:40完全消耗系数矩阵为:3•其他条件不变，当本地产品最终需求为W =(224 400 350)'时，各部门产品的总产出为：X = [l - A d ∖∖γd + F}^ 1.1217 0.092 0.1 15 ^Z"224"-76]]0.25881.0469 1.3086400 + 180 -0.181 1 -0.73284.084350 ■ ■UJ430.1409 I 142.853 950.00290.1217 0.2588 -0.18HIOOO 20IOOO 40 600 IO 0.01 0.01 0」25 0.08 00.040 0.0333 0.0167I000 6000.01 0.01= ∕l κ(/0.125 0.08_ 00.040.0115 0.011 0.0004'0.1376 0.09010.03690.0056 0.04430.01850 -0.0333 0.9833400 400 80-0.01 0.92 -0.043•其他条件不变，当本地产品最终需求为Y it = (224 400 35Oy时，计划期地区投入产出表的第I 象限流量矩阵为:-0.090,08 0 1 Γ430.1409 0 0 " [<]= A ti X = 0.22502 025 θ1142.853.00.140.2」 [0950.002938.712791.428296.7817 228.5706 237+5007159.9994190.0006■时，计划期地区投入产出表的第In 象限流量矩阵为:第五章课后习题第4题播下列般入严吐井算各部ΓL⅛: O tL ⅛⅜⅛⅜⅛; _S 全消耗集⅛t∙(it⅛⅛ 3 部口的豪堆严諾的需求童为“亿元比， *∕<M⅛入产岀表.3•其他条件不变，当本地产品最终需求为^=(224400 35Oy■ 0.01 0.01 0 ] —A X X = 0.125 0.080.03330,04 0.0167」^4.301411.42850 ]= 53.7676 91.428231.6351Si45.7141 15.8650」I 142.853950,0029430.14091010 单位：10丄4(1)本地区部门产品的直接消耗系数为:0.1064 0.4256 0.2766 0.1064 0.4255 0.3830.53180.12770.1064 0.4256 0.7021(3)输入产品的直接消耗系数为:"0.80 —0.2 -I0 0"B j = (I-A J y-I =-0.2 0.6667 0— 0 1 0.0-0.1667 0.60 0 1(2)本地区部门产品的完全消耗系数为:1.2766 0.1064 0.4255I 0 020 IO O 20IOO 00 60 20 60 IO60 IO 50 50 2050 0.2 0.20 0.3333 0.16670.2 0 0.40.3831.5318 0.1277 一 0 0-500-500-50θ605一605-60 101 OOOOOOOO一 ■=K0」 0 0 =00.0833 0 00.08331.7021 0 0(3)输入产品的完全消耗系数为:'0.1O O - '0.9 O O - 屮（/_旳"=O 0.0833 O O 0.9167 O O0.0833O■ O-0.0833 1OlO 0' Illll O 0' O0.0833 O O1.0909 O O0.0833O O 1»0.0909 I0.1111 O ■ O O0.0909 O O0.0909O(4)若各系数不变，计划期各部门最终产品需求为:Y d =(75 30 20)z则，本地区部门的总产出为："1.2766 0.1064 0.4255''15-i07.4476' X^l-A d yY d =0.383 1.5318 0.1277 30 = 77.23040.1064 0.4256 1.7021 ■ ■ 20 ■ ■54.7905 ■ ■计划期地区投入产出表的第I 象限流量矩阵为:0.2O=A d X =0.2 0.3333L VJ 3×3O 0.1667"21.4895O10.958 Γ=21.4895 25.7409OO12.8743 21.91620.2 107.4476O O OO 77.2304 O 0.4OO54.7905_计划期地区投入产出表的第III 象限流量矩阵为:'0.10 ■ 0 "107.4476 0 0 凶L =A g X =0 0.0833 0 0 77.2304 0_ 00.083354.790510.74480'—6.4333 0.06.4333 0报告期劳动者报酬系数列向量为:且由公式：则，计划期劳动者报酬列向量为:K = (0.25×107.4476 0.1667×77.2304 0.2×54.7905/ = (26.8619 12.8743 10.958 l)z报告期生产税净额和营业盈余报酬系数列向量为：且由公式：m l= U ItiI X i则，计划期生产税净额和营业盈余报酬列向量为:M = (0.25x107.4476 0.1667×77.2304 0.2 × 54.7905/ =(26.8619 12.8743 10.9581/A V =251010、100 60 50=(0.25 0.16670.2/AnI_ f 25__ .Tδδ 10 60]θY 50>= (0.25 0」667 0.2),计划期投入产出表为:第六章直接消耗系数矩阵单位=吨(除注明单位外)(1)如果该厂计划下阶段生产钢材最终产品100吨，那么其他自产产品总产量和外购产品的消耗量应该如何安排？(2)在计划生产过程中，由于某种原因需要调整计划，原计划销售钢坯 80吨、钢材100吨，现调整追加到钢坯 100吨、钢材150吨。

投入产出技术考题2006/6/14一、 已知纯部门直接消耗系数矩阵A ，产出矩阵（制造矩阵）V ，试列出混合部门直接消耗系数矩阵A 的计算公式及依据。

（其他数都不知道） 二、 对如下投入产出表：1、对本国产品的直耗系数矩阵D A 和完全消耗系数矩阵D B 。

2、对进口产品直耗系数矩阵M A 和完全消耗系数矩阵M B 。

三、 在上述投入产出表中用开模型方法计算1、各部门增加出口一个单位，对该国GDP 的影响和对工资额的影响,并列出计算公式。

2、 如果出口列向量为(12,20,0)T 时，试计算出口增加对各部门增加值和工资额，以及GDP 变动的影响。

四、 如果国民经济各部门单位产品中的税收提高α倍, 即 10Tj Tj a a α=(0Tj a 为j 部门原来的单位产品中的税收数额)，并假设①不实行固定价格制，产品价格随成本提高而提高，②其它条件即利润、工资等均不变, 试计算税收变动对各部门价格的变动.（请在2006年7月3日前交到大楼434房间，每日上午有人；或送到大楼收发室54号信箱陈锡康收；或用Email 发送- Email Address: xkchen@ ）答案一、i nj ij G V =∑=1（i=1，2，…，n ）令jji ij GV c =， 1ˆ-=GV C T 又j ni ij Q V =∑=1，故j ni i ji Q G C =∑=1，即CG=Q令jij ij QV d =， D=V 1ˆ-Q商品工艺假定 U=A V T ，若b ij 表示j 部门单位总产出所投入的i 种产品的产值，则B 为产品×部门投入系数矩阵。

有1ˆ-=GU B 部门工艺假定 A =BD1）在市场份额基础上进行推算W=DU 而 1ˆ-=GW A 如采用的是商品工艺假定，则11ˆˆ--=G AV QV A T 而 G GV Q T 1ˆ-= 因为 G=（∑=n j j V 11，∑=n j j V 12，…，∑=nj nj V 1）T ，所以G ˆ=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∑∑∑===nj njnj jnj j V V V 112111ˆ-G =⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∑∑∑===nj njnj jn j j V V V 11211111因Q=（∑=ni i V 11，∑=ni i V 12，…，∑=ni in V 1）T ，故=Q ˆ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∑∑∑===ni inni i ni i V V V 112111ˆ-Q=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∑∑∑===ni inni i n i i V V V 11211111如采用的是部门工艺假定，则1ˆ-GU D=A 所以 U=A GD ˆ1==A GV Q ˆˆ1- 因此11ˆˆ--=V Q A QV A2）在部门制造比例假定基础上进行推算U=CW所以 A C G CW GU ==--11ˆˆ 于是 11ˆ=-=GU C A 如采用商品工艺假定，则11ˆˆ--=GAVV G A TT ）（ 如采用部门工艺假定，则11ˆˆ--=V QA V G A T ）（二、答案：1．对本国产品的直耗系数矩阵A DA D =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡2.01.0003.01.04.002.0501010010100050010030100105020100010020 I －A D =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---8.01.0007.01.04.000.8，（I －A D ）－1=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡2613.11802.00225.00901.04414.11802.06306.00901.02613.1（在Excel2002中计算）完全消耗系数矩阵B D =（I －A D ）－1－I=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡2613.01802.00225.00901.04414.01802.06306.00901.02613.0 2．对进口产品直耗系数矩阵A MA M =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡1.00001.01.0001.050510001000500100101001050010******* I －A M =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-9.00009.01.0000.9，（I －A M ）－1=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1111.10000.00000.00000.01111.11235.00000.00000.01111.1（在Excel2002中计算） 完全消耗系数矩阵B M =（I －A M ）－1－I=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1111.00000.00000.00000.01111.01235.00000.00000.01111.0 三、答案：1． Y '=（61，61，31）T⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡='-='- 51.4640 101.7117 101.98203161612613.11802.00225.00901.04414.11802.06306.00901.02613.11Y A I X D ）（ 增加值率矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=∑∑∑===6.04.03.0ˆ313312311i Di i Di i Di a a a C ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡='-=' 20.5856 61.0270 71.3874 51.4640 101.7117 101.98204.06.07.0ˆX CI V ）（ ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=-'=∆5856.50270.113874.21155050 20.5856 61.0270 71.3874V V V ∆GDP=21.3874+11.0270+5.5856=38对工资的直接投入系数矩阵为A W =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡20.015.020.050101001510020⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡='=' 10.292815.2568 20.396451.4640 101.7117 101.982020.015.020.0X A W W⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=-'=∆2928.02568.03964.0101520 10.2928 15.256820.3964W W W 2． ∆E=TT T E E ），，（），，（），，（0520151002012=-=-'TT T E Y Y ），，（），，（），，（306562052306060=+=∆+='⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡='-='- 50.9459 107.5676 102.97303065622613.11802.00225.00901.04414.11802.06306.00901.02613.11Y A I X D ）（ ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡='-=' 20.3784 64.5405 72.0811 50.9459 107.5676 102.97304.06.07.0ˆX CI V ）（ ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=-'=∆3784.55405.140811.22155050 20.3784 64.5405 72.0811V V V ∆GDP=22.0811+14.5405+5.3784=42 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡='=' 10.1892 16.1351 20.5946 50.9459 107.5676 102.973020.015.020.0X A W W⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=-'=∆1892.01351.05946.0101520 10.1892 16.135120.5946W W W 四、以V 表示增加值，以P 表示价格，A 表示直耗系数矩阵，则V A I P T ∆-=∆-1）（当税收提高为原来的α倍时，00001)1(Tj Tj Tj Tj Tjj a a a a a V -=-=-=∆αα 故01)1(T T a A I P --=∆-α）（。

投入产出法习题答案第三章第三章：投入产出法习题答案在经济学中，投入产出法是一种用于衡量经济活动的方法。

它通过分析不同产业之间的投入和产出关系，来评估经济的发展和效益。

本文将对投入产出法习题的答案进行探讨，以帮助读者更好地理解这一经济学工具。

1. 习题一：某国家的投入产出表显示，农业部门的总产出为1000亿元，其中农业部门对其他部门的需求为200亿元。

根据这些数据，计算农业部门的直接需求系数和总需求系数。

答案：直接需求系数等于农业部门对其他部门的需求除以农业部门的总产出，即200/1000=0.2。

总需求系数等于农业部门的总需求除以农业部门的总产出，即(200+1000)/1000=1.2。

2. 习题二：某国家的投入产出表显示，农业部门的总需求为400亿元，其中对农业部门的直接需求为100亿元。

根据这些数据，计算农业部门的直接供给系数和总供给系数。

答案：直接供给系数等于对农业部门的直接需求除以农业部门的总需求，即100/400=0.25。

总供给系数等于农业部门的总供给除以农业部门的总需求，即(100+400)/400=1.25。

3. 习题三：某国家的投入产出表显示，农业部门的总需求为500亿元，其中对其他部门的需求为100亿元。

根据这些数据，计算农业部门的直接供给系数和总供给系数。

答案：直接供给系数等于农业部门对其他部门的需求除以农业部门的总需求，即100/500=0.2。

总供给系数等于农业部门的总供给除以农业部门的总需求，即(100+500)/500=1.2。

通过以上习题的答案计算，我们可以看出直接需求系数和直接供给系数反映了不同部门之间的相互依赖程度。

直接需求系数越高，说明该部门对其他部门的需求越大，反之则越小。

直接供给系数越高，说明该部门对其他部门的供给越多，反之则越少。

总需求系数和总供给系数则反映了整个经济系统的需求和供给情况。

总需求系数大于1表示总需求超过了总产出，说明经济处于扩张状态；总需求系数小于1表示总需求不足，说明经济处于萎缩状态。

部分习题参考答案答1：价值型投入产出表分为中间流量、最终使用、增加值三个象限。

第一， 象限采用复式记帐的矩阵形式，反映国民经济各个部门的经济技术联系；第二、第三象限分别反映最终使用和增加值的构成。

三个象限实际上表示了国民生产总值的三种计算方法。

答2：（1） 行平衡关系：中间使用＋最终使用＝总产出1i=1,2,,n niji i j xY X =+=∑ （）该平衡关系把投入产出表的第一、二象限联系起来，反映产品的分配使用去向,即反映产品的实物运动； （2） 列平衡关系：中间投入＋增加值＝总投入nijj j j j j i=1x+D +V +T +M =X (j=1,2,,n)∑该平衡式把投入产出表的第一、三象限联系起来，反映产品的价值构成，即反映了产品的价值运动； （3） 其他平衡关系A. 同一部门的平衡关系――各部门的总产出与总投入相等，也就是同一部门的生产方程与分配方程相等：11nnkjk ik k j i xY x N ==+=+∑∑B. 整个国民经济的平衡关系――全社会的总产出与总投入相等，也就是全社会的生产总值与使用总值相等。

11n ni ji j Y N===∑∑答3：基本的投入产出参数是进行投入产出分析和研究的基础。

引进投入产出参数的目的是在投入产出平衡关系的基础上建立投入产出模型。

最主要的投入产出参数是直接消耗系数、完全消耗系数、完全需求系数、增加值构成系数等。

其中直接消耗系数是最基本的系数，不仅是因为它可以直接由投入产出表计算得到，而且通过它才能计算出完全消耗系数和完全需求系数。

解8：直接消耗系数0.0345 0.0367 0.0000 0.0103 0.3563 0.4301 0.3033 0.1554 0.0115 0.0047 0.0205 0.0183 0.1034 0.1147 0.1311 0.2287完全消耗系数0.0669 0.0749 0.0272 0.02990.7485 0.8898 0.6395 0.40600.0210 0.0155 0.0294 0.02790.2580 0.2938 0.2738 0.3657投入矩阵0.9655 -0.0367 0.0000 -0.0103 -0.3563 0.5699 -0.3033 -0.1554 -0.0115 -0.0047 0.9795 -0.0183 -0.1034 -0.1147 -0.1311 0.7713完全需求系数矩阵1.0669 0.0749 0.0272 0.0299 0.7485 1.8898 0.6395 0.4060 0.0210 0.0155 1.0294 0.0279 0.2580 0.2938 0.2738 1.3657 解9步骤1：由ij ij jx a X =得X 1=600步骤2：由ij ij j x a X =算出x i1和x i2 步骤3：由()1c X I A N -=-，得X 3=1200步骤4：由（30＋60＋16）+0.1X 4+164=X 4 ,解出X 4 。

投入产出法习题答案投入产出法（Input-Output Analysis）是一种经济分析方法，用于衡量不同产业之间的相互依赖关系和经济活动对整体经济的影响。

它通过建立一个输入产出表，展示了各个产业之间的交互作用，从而揭示了经济系统的内在结构和运行规律。

在这篇文章中，我们将回答一些投入产出法的习题，以帮助读者更好地理解和应用这一分析工具。

首先，让我们来看一个简单的投入产出表。

假设一个经济系统由两个产业组成：农业和制造业。

农业生产50单位的农产品，并将其中的40单位用于自身消费，剩下的10单位用于向制造业提供原材料。

制造业使用这10单位的农产品作为原材料，并生产出20单位的制成品。

制造业将其中的15单位用于自身消费，剩下的5单位用于出口。

根据这个投入产出表，我们可以计算出经济系统的总产出、总消费和总出口。

首先，计算总产出。

农业的产出是50单位，制造业的产出是20单位，所以总产出是50 + 20 = 70单位。

接下来，计算总消费。

农业的自身消费是40单位，制造业的自身消费是15单位，所以总消费是40 + 15 = 55单位。

最后，计算总出口。

制造业的出口是5单位，所以总出口是5单位。

通过这个简单的例子，我们可以看到投入产出法的基本原理。

它通过追踪不同产业之间的交互作用，揭示了一个经济系统的内在联系和相互依赖关系。

这对于制定经济政策和预测经济发展趋势非常重要。

接下来，让我们来看一个更复杂的例子。

假设一个经济系统由三个产业组成：农业、制造业和服务业。

农业生产100单位的农产品，并将其中的80单位用于自身消费，剩下的20单位用于向制造业提供原材料。

制造业使用这20单位的农产品作为原材料，并生产出40单位的制成品。

制造业将其中的30单位用于自身消费，剩下的10单位用于向服务业提供原材料。

服务业使用这10单位的制成品作为原材料，并提供出口服务20单位。

服务业将其中的15单位用于自身消费，剩下的5单位用于出口。

根据这个投入产出表，我们可以计算出经济系统的总产出、总消费和总出口。

《投入产出分析》习题及解答陈正伟2010-05-26第一章投入产出法概论1、投入产出法：作为一种科学的方法来说，是研究经济体系（国民经济、地区经济、部门经济、公司或企业经济单位）中各个部分之间投入与产出的相互依存关系的数量分析方法。

－名词解释、填空2、国民经济：是指由一系列纵横交错的各种经济活动组成的有机整体。

本处研究的投入产出表实际上就是国民经济投入产出表。

－名词解释、填空3、投入：是指在一定时期内的生产经营过程中所消耗的原材料、燃料、动力、固定资产折旧、劳动力和支付的各种费用及利润、税金等项目的总和。

－名词解释4、下列属于投入产出分析中的投入有（）A 原材料B 固定资产折旧C 贷款利息支出D 劳动者报酬E 生产税5、下列属于投入产出分析中的投入有（）A 原材料B 固定资产折旧C 国家给予职工的物价补贴D 劳动者报酬E 生产税6、下列属于投入产出分析中的投入有（）A 获得的捐赠物质B 国家的奖金C 国家给予职工的物价补贴D 劳动者报酬E 生产补贴7、产出：是指一定时期内生产经营的总成果及其分配使用去向。

－名词解释8、某地区总投入为3000亿元，中间投入为2000亿元，则各地区总产出为（）亿元。

A 3000B 2000C 1000D 50009、在投入产出分析中下列关系成立（）。

A 总投入＝总产出B 总产出＝中间使用＋最终使用C 总投入＝中间投入＋最初投入D 总投入＝中间投入＋增加值E 各个部门增加值总和＝全社会最终使用总和10、在投入产出分析中下列关系成立（）。

A 总投入＝总产出B 总产出＝中间使用C 总投入＝增加值＋最初投入D 总投入＝中间投入＋最终使用E 各个部门增加值总和＝全社会总产出的总和11、投入产出法的基本内容：编制投入产出表、建立相应的线性代数方程体系，综合分析和确定国民经济各部门之间错综复杂的联系，分析重要的宏观经济比例关系及产业结构等基本问题。

简答12、投入产出表；是指反映各种产品生产投入来源和使用去向的一种（矩阵）棋盘式表格。

国民经济核算第三章投入产出核算第三章投入产出核算§1 投入产出表的结构与内涵§2 投入产出表的数据口径§3 编制投入产出表的调查方法§4 编制投入产出表的非调查方法§5 投入产出表的应用学习目的与要求第一、掌握投入产出表的基本思想及表中元素的实际意义第二、掌握投入产出核算与国内生产总值核算的关系第三、了解编制投入产出表的调查方法第四、掌握用非调查方法编表的技术第五、掌握运用投入产出表进行经济分析的思路和方法§1 投入产出表的结构与内涵一、华西里·列昂惕夫的简介二、投入产出表入门三、根据投入产出表进行GDP核算四、投入产出表的优势一、华西里·列昂惕夫简介沃西里·列昂惕夫(Wassily Leontief,1906-1999)，美籍俄裔著名经济学家。

1973年诺贝尔经济学奖获得者。

沃西里·列昂惕夫生平1、1906年，出生于彼得堡；2、1925年，在列宁格勒大学（后改名为彼得堡大学）获社会学硕士学位；同年，移居德国进入柏林大学专攻经济学；3、1928年，取得柏林大学哲学博士学位；曾任德国基尔大学世界经济研究所研究助理、中国国民党政府铁道部顾问。

4、1931年，移居美国在哈佛大学经济系任教，正式从事投入产出方法的研究。

5、1932年，与诗人马克丝(Estelle Marks)结婚，婚后育有三子。

6、1932年，起获聘为哈佛大学经济系助教；7、1946年，升为正教授至1975年退休。

8、1948年，主持“哈佛经济研究计划”(Harvard Economic Research Project)并出任主持人至1973年；9、 1974年，联合国委托里昂惕夫建立全球性投入产出模型，以研究本世纪最后的20多年中世界经济可能发生的变化与国际社会能够采取的方案。

10、 1975年，转至纽约大学任经济学教授、经济分析研究所所长。

第三章投入产出核算一、基本概念投入产出表产品部门产业部门购买者价格生产者价格产品工艺假定部门工艺假定RAS法改进RAS法直接消耗系数影响分析完全消耗系数影响力系数感应度系数二、思考题1.试述投入产出表中四个象限各自所包含的内容。

2.在投入产出表中，如何实现国内生产总值三种计算方法？投入产出表的优势体现在哪里？3.直接消耗系数与完全消耗系数的经济含义是什么？二者有何区别？三、练习题（一）填空题1.投入产出表记录的数据可以分为三类：第一类是______，可以从使用和投入两个方向解读；第二类和第三类分别是_________和_________，它们都只具有一种含义。

2.在各类投入产出表中，产品×产业表反映的是各产业部门______的信息，而产业×产品反映的是各产业部门_______的信息，由于这两类表编制所需数据可以从现有统计体系中较容易获得，故常用于推算产品×产品表。

3.影响力系数表现的是拉动效应，显示的是_____联系；感应度系数表现的是对其他部门变化的敏感效应，反映的是_____联系。

答案：1. 中间流量数据最终使用数据最初投入数据2. 投入结构所生产的产品结构3. 后向前向（二）单项选择题1.投入产出表中，第三产业行与第一产业列交叉项的数值，从横向上看表示_______，从列向上看表示_______。

A.第三产业部门在生产过程中消耗第一产业部门的产品数量B.第三产业部门的产品提供给第一产业部门作为生产消耗使用的数量C.第一产业部门在生产过程中消耗第三产业部门的产品数量D.第一产业部门的产品提供给第三产业部门作为生产消耗使用的数量2.一家企业主要生产钢铁，同时从事小规模的煤炭开采和炼焦，则在编制投入产出表时该企业创造的总产出应该计入_______。

A. 钢铁业B. 炼焦业C. 煤炭开采业D. 分别计入以上三个产业部门3.在一个三产业投入产出表中，直接消耗系数a21的数值为0.2864，则它所代表的含义是_________。

第三章_投入产出核算习题_答案)国民经济核算国民经济核算第三章投入产出核算(一)填空题投入产出表的核心是第Ⅰ象限， 1. 投入产出表的核心是第Ⅰ象限，它主要反映了国民经济各产业部门之间的相互依存、相互制约的技术经济联系。

部门之间的相互依存、相互制约的技术经济联系。

2.购买者价格与生产者价格的差异在于商业附加费和运输费。

2.购买者价格与生产者价格的差异在于商业附加费和运输费。

购买者价格与生产者价格的差异在于商业附加费和运输费 3.投入产出表的编制方法主要包括直接分解法和间接推导法两种模 3.投入产出表的编制方法主要包括直接分解法和间接推导法两种模投入产出表的编制方法主要包括直接分解法式。

4.直接消耗系数指某部门为生产单位产品所消耗的各种中间投入的 4.直接消耗系数指某部门为生产单位产品所消耗的各种中间投入的直接消耗系数指某部门为生产单位产品所消耗的各种中间投入数量。

数量。

5.影响力系数表现的是拉动效应，显示的是后向联系； 5.影响力系数表现的是拉动效应，显示的是后向联系；感应度系数影响力系数表现的是拉动效应后向联系表现的是对其他部门变化的敏感效应，反映的是前向联系。

前向联系表现的是对其他部门变化的敏感效应，反映的是前向联系。

新疆财经大学国民经济核算国民经济核算(二)单项选择题1.投入产出分析的核心内容和重要工具是_A_ 1.投入产出分析的核心内容和重要工具是_A_ 投入产出分析的核心内容和重要工具是 A. 投入产出表 C. 资产负债表 B. 资金流量表 D. 国际收支平衡表2.投入产出表是两张普通统计表的组合，其上半部分反映了C . 2.投入产出表是两张普通统计表的组合，其上半部分反映了C 投入产出表是两张普通统计表的组合 A. 生产的投入结构 C. 产品的使用方向 B. 生产的产出结构 D. 收入的分配结构新疆财经大学2国民经济核算国民经济核算3.投入产出表中，第三产业行与第一产业列交叉项的数值， 3.投入产出表中，第三产业行与第一产业列交叉项的数值，从横向投入产出表中上看表示_B__ 从列向上看表示C _B__, 上看表示_B__,从列向上看表示C 。

第一章国民经济核算的基本理论(三)名词解释1．国民经济核算，简称国民核算，是指对国民经济运行过程的系统描述，是了解经济运行和经济发展，发现问题、分析规律、为经济决策服务的重要信息资源。

2．国民经济机构单位是指有权拥有资产和承担负债，能够独立从事经济活动和与其他实体进行交易的经济实体。

国民经济机构单位根据其主要经济职能、行为和目的的基本特征分类形成国民经济机构部门。

3．国民经济基层单位是国民经济核算体系中为了进行生产核算和投入产出+分析确定的基本核算单位，在我国统计部门也称为产业活动单位。

国民经济基层单位根据生产产品或服务的同质性分类形成国民经济产业部门，在我国习惯称国民经济行业部门。

4．经济流量是反映一定时期内所有经济活动变化的价值数量，包括生产、分配和再分配、变换、流通、使用，以及资产和负债、物量和物价的变化的价值量。

经济存量是反映某一时点的资产和负债状况的价值量。

5．要素价格是根据劳动报酬、固定资本消耗和营业盈余确定的价格形式。

6．基本价格是根据要素价格和产品税以外的生产税的构成因素确定的价格形式。

7．生产者价格是指生产者单位产品的市场价格，包括要素价格和单位产出的生产税净额。

8．购买者价格是指购买者购买单位产品应支付的市场价格。

9．三等价原则是指国民经济运行过程中国民生产、国民(原始或可支配)收入和国民(最终)支出之间的总量平衡关系的等价统计原则。

10．权责发生制原则是指对经济活动中机构单位之间交易按照其债权债务发生时、或生产活动中价值转移或新价值形成或取消时进行统计的原则。

（四）简答题1．答：国民经济机构部门包括（1）非金融企业部门，由从事生产市场上的产品和非金融服务的法人企业组成。

（2）金融机构部门，由从事金融媒介活动的所有常住法人单位和企业组成。

(3)政府部门，由具备法人资格的各种类型的行政单位和非企业化管理的事业单位组成。

(4)住户部门，由所有常住居民住户组成。

(5)为居民服务的非营利机构部门，它是法律实体，不以追求利润为目的，主要从事为居民家庭生产非市场性服务，其活动经费主要是由各种捐赠的资金来源负担。

企业经营统计学课后习题答案汇总（李宝瑜、刘洪主编）目录第一章绪论.............................................................................................................................. - 1 -第二章企业市场调查与预测.................................................................................................. - 2 -一、单项选择题.................................................................................................................. - 2 -二、多项选择题.................................................................................................................. - 2 -三、计算题.......................................................................................................................... - 3 -第三章企业投入与产出统计.................................................................................................. - 3 -一、单项选择题.................................................................................................................. - 3 -二、多项选择题.................................................................................................................. - 4 -三、计算题.......................................................................................................................... - 4 -第四章企业质量统计与监控.................................................................................................. - 6 -一、单项选择题.................................................................................................................. - 6 -二、多项选择题.................................................................................................................. - 7 -三、计算题.......................................................................................................................... - 7 -第五章企业经营统计分析...................................................................................................... - 8 -一、单项选择题.................................................................................................................. - 8 -二、多项选择题.................................................................................................................. - 8 -四、计算题.......................................................................................................................... - 9 -第六章企业客户关系统计.................................................................................................... - 10 -一、单项选择题................................................................................................................ - 10 -二、多项选择题................................................................................................................ - 11 -三、计算题........................................................................................................................ - 11 -第七章企业人力资源统计.................................................................................................... - 13 -一、单项选择题................................................................................................................ - 13 -二、多项选择题................................................................................................................ - 14 -三、计算题........................................................................................................................ - 14 -第九章企业财务评价与经济效益统计................................................................................ - 15 -一、单项选择题................................................................................................................ - 15 -二、多项选择题................................................................................................................ - 16 -三、计算题........................................................................................................................ - 16 -第一章绪论一、单项选择题1.公开出版和不公开出版的各种年鉴和资料汇编属于（D）A.企业内部直接资料B.企业外部直接资料C.企业内部间接资料D.企业外部间接资料2.统计报表属于（D ）A.数据的录入B.数据的编辑C.数据的存贮D.数据的利用3.企业经济效益统计分析报告属于（B）A.计划性的统计分析报告B.综合性统计分析报告C.专题性统计分析报告D.预测性统计分析报告4.企业经营统计学的研究对象是（A）A.企业生产经营活动的数量及关系B.统计工作C.企业经济的内在规律性D.统计方法5.下列哪些不属于原始记录（A）A.汇总表B.领料单C.发货单D.考勤表二、多项选择题1.企业作为社会生产的基本生产单位，其基本特征有（ABCDEF）A.企业是一个以盈利为目的的经济组织B.企业直接为社会提供产品或服务C.企业是一个独立核算的主体D.企业拥有经营权E.企业行使独立的职能F.企业是具有法人资格的独立经济实体2.根据企业所有制性质及有关法律规定分类，企业可分为（AC）A.公有经济和国有经济B.集体经济C.非公有经济D.私有经济E.港澳台经济和外商经济3.按照企业生产要素密集程度，通常企业可分为( ABC )A.资金密集型B.劳动密集型C.技术(知识)密集型D.要素密集型E.资源密集型4. 企业经营统计学的特点（ABD）A.数量性B.具体性C.个体性D.总体性E.社会性5.企业统计数据的存贮形式主要有（CDE）A.统计报表B.统计分析报告C.统计汇总D.综合性台账E.专门性台账第二章企业市场调查与预测一、单项选择题1.能反映被调查者的态度层次，能表示各答案之间的等级顺序，但不能用加减乘除计算答案之间的差距值和倍数的测量表是（B）A.定距量表B.定序量表C.定比量表2.中间商预测法具体方法有（A）A.定单预测法B.定货量表C.ABC预测法3.在一次指数平滑法中，当环境影响因素比较多或者影响程度比较大时，平滑系数 的取值一般为（C）A.0.05-0.3之间B.0.3-0.6之间C.0.6-0.9之间4.因果性调查一般采用（D）方法A.抽样法B.问询法C.观察法D.试验法二、多项选择题1.市场调查的类型有：( ABCD )A.探测性调查B.描述性调查C.因果性调查D.预测性调查E.价格调查2.市场调查常用的调查方法有：（ABDE）A.抽样法B.文案法C.询问法D.观察法E.实验法3.问卷的构成要素：（ABCDE）A.被调查者基本情况B.调查的具体项目C.问卷填写说明D.编号E.调查者项目4、问卷设计的程序：（ABCD）A.确定设计主题B.设计问卷初稿C.进行试验性调查D.设计正式问卷E.调查报告三、计算题1.某商店1-10月份销售额如下，取n=3，试用趋势移动平均法预测11月份的销售额。

复习思考题1.简述工业生产企业生产过程的核算。

答：生产过程是工业生产企业资金循环的第二阶段。

再生产过程中发生的各种耗费，称之为生产费用。

生产核算就是把这些费用，按一定种类的产品进行归集和分配，以计算产品的生产成本，生产过程核算主要任务是：核算与监督生产费用的发生和分配，产品生产的品种、数量和质量；计算产品成本，考核生产资金定额和成本计划的执行情况；反映生产过程中的问题，总结经验，降低成本，提高效益。

2.成本计算的基本要求是什么？答：成本计算过程实际上是费用的归集和分配过程，要做好成本计算工作，必须准确归集和分配各种费用。

一般要做到一下三点：1. 按规定的成本内容进行确认和计量。

会计确认的标准：a：符合某项要素的定义：b：能够可靠的加以计量。

会计计量属性包括：历史成本、重置资本、可变现净值、现值和公允价值。

2. 划清支出与费用、费用与成本的界限。

3. 按权责发生制原则进行成本计算。

权责发生制: 就是应收应付制，是以应收和应付作为标准来确定本期的收益和费用，凡属于本期的收益和费用，不论是否已经收入或支付，都作为本期的收益和费用处理，而不属于本期的收益和费用，即使已经实际收入或支付了，都不能作为本期的收益和费用。

3.如何核算产品制造成本？答：产品制造成本的计算，就是按照生产的各种产品，归集和分配在生产过程中所发生的各种费用，并按成本项目计算各种产品的总成本和单位成本。

制造成本是指生产活动的成本，即，企业为生产产品而发生的成本。

制造成本是生产过程中各种资源利用情况的货币表示,是衡量企业技术和管理水平的重要指标。

制造成本是生产单位为生产产品或提供劳务而发生的各项生产费用，包括各项直接支出和制造费用。

直接支出包括直接材料（原材料、辅助材料、备品备件、燃料及动力等）、直接工资（生产人员的工资、补贴）、其他直接支出（如福利费）；制造费用是指企业内的分厂、车间为组织和管理生产所发生的各项费用，包括分厂、车间管理人员工资、折旧费、维修费、修理费及其他制造费用（办公费、差旅费、劳保费等）。