分水岭算法的Matlab实现

分水岭分割算法的实现 与分析
青 衣
11053413 李小泷
• 分水岭算法实现步骤：先把图片转化为灰度梯度级图像， 在图像梯度空间内逐渐增加一个灰度阈值，每当它大于一 个局部极大值时，就把当时的二值图像(只区分陆地和水 域，即大于灰度阈值和小于灰度阈值两部分)与前一个时 刻(即灰度阈值上一个值的时刻)的二值图像进行逻辑异或 (XOR)操作，从而确定出灰度局部极大值的位置 。根据所 有灰度局部极大值的位置集合就可确定分水岭。
Lrgb = label2rgb(L, 'jet', 'w', 'shuffle');%转 化为伪彩色图像 subplot(122); imshow(Lrgb)%显示伪彩色图 像 title('分水岭伪彩色图像') 青 衣
figure; imshow(I), hold on himage = imshow(Lrgb);%在原图上显示 伪彩色图像 set(himage, 'AlphaData', 0.3); title('原图像上的Lrgb处理')
imcomplement(Iobr));%形态学重建 Iobrcbr = imcomplement(Iobrcbr);%图像求反 subplot(122); imshow(Iobrcbr), %显示重建求反后的 图像 title('重建求反后的图像(Iobrcbr)')
fgm = imregionalmax(Iobrcbr);%局部极大值 figure; imshow(fgm), %显示重建后局部极大值图像 title('重建后局部极大值图像(fgm)')
此时再进行分水岭变换并显示得到的效果。

% These operations will create flat maxima inside each object that can be located using imregionalmax.
% 有多种方法可以应用在这里来获得前景标记，这些标记必须是前景对象内部的连接斑点像素。这个例子中，将使用形态学技术“基于开的重建”和“基于闭的重建”来清理图像。
% 接下来，通过腐蚀后重建来做基于开的重建计算。
Ie = imerode(I, se);
Iobr = imreconstruct(Ie, I);
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(1, 2, 1); imshow(I, []); title('灰度图像');
% 使用MATLAB图像处理工具箱
% 注：期间用到了很多图像处理工具箱的函数，例如fspecial、imfilter、watershed、label2rgb、imopen、
% imclose、imreconstruct、imcomplement、imregionalmax、bwareaopen、graythresh和imimposemin函数等。
% The gradient is high at the borders of the objects and low (mostly) inside the objects.
% 使用Sobel边缘算子对图像进行水平和垂直方向的滤波，然后求取模值，sobel算子滤波后的图像在边界处会显示比较大的值，在没有边界处的值会很小。
figure('units', 'normalized', 'position', [0 0 1 1]);

n r 数 h(rk ) nk 表示。其中， k 是第K级灰度， k 是灰
度级为 rk的像素个数。
通常迚行归一化处理，n是图像中像素的总数 n p ( rk ) k ，我们也可以称为 n 灰度级为 rk 发生的概率估计。且各级相加之和为
1
提出一种想法：若一副图像的像素占有全部可能的灰度 级并且分布均匀，那么这幅图像就会有较高的对比度，
直方图匹配
第二部分
形态学操作
膨胀不腐蚀
1
4
区域填充
开操作不闭操 作
2
形态学
5
连通分量的提 取
击中击丌中变 换
3
6
重构
腐蚀
把结构元素S平移x后得到Sx，若Sx包含于X，我们记下这个x点，所有满 足上述条件的x点组成的集合称做X被S腐蚀(Erosion)的结果。用公式表示为：
腐蚀的方法是，拿S的原点和X上的点一个一个地对比，如果S上的所有点 都在X的范围内，则S的原点对应的点保留，否则将该点去掉。
最近工作汇报
前 言
首先自我检讨一下，来这边整整一个月的时间，说真的并没有把时间
分配处理的很好，常常处在一种困惑的阶段，时丌时得干劲十足，可能一 段时间之后又失去方向了。。。丌过丌管怎么样，还是在一定程度上有所
迚步，首先是渐渐收敛了玩的心，再者就是戒多戒少学到了一些知识，希
望在今后的日子里，可以更好得利用自己的学习时间，提高效率，和大家 沟通交流，自己也能有更多的IDEA，再接再励 O(∩_∩)O
且灰度级动态范围大
直方图均衡
直方图均衡化：顾名思义，就是通过灰度变换将一幅图象转换 为另一幅具有均衡直方图，即在每个灰度级上都具有相同的象 素点数的过程， Ps ( s ) 1 直方图均衡化变换：设灰度变换s=T(r)为斜率有限的非减连续 可微函数，它将输入图象Ii(x，y)转换为输出图象Io(x，y)，输 入图象的直方图为Hi(r)，输出图象的直方图为Ho(s)，则根据直 方图的含义，经过灰度变换后对应的小面积元相等： Ho(s)ds=Hi(r)dr

程序代码：(代码标记[code]...[/code] )clear,clc%三种方法进行分水岭分割%读入图像filename='Fig1021(a)(small-blobs).tif';f=imread(filename);Info=imfinfo(filename);if Info.BitDepth>8f=rgb2gray(f);endfigure,mesh(double(f));%显示图像，类似集水盆地%方法1：一般分水岭分割，从结果可以看出存在过分割问题b=im2bw(f,graythresh(f));%二值化,注意应保证集水盆地的值较低（为0），否则就要对b取反d=bwdist(b); %求零值到最近非零值的距离，即集水盆地到分水岭的距离l=watershed(-d); %matlab自带分水岭算法，l中的零值即为风水岭w=l==0; %取出边缘g=b&~w; %用w作为mask从二值图像中取值figuresubplot(2,3,1),imshow(f);subplot(2,3,2),imshow(b);subplot(2,3,3),imshow(d);subplot(2,3,4),imshow(l);subplot(2,3,5),imshow(w);subplot(2,3,6),imshow(g);%方法2：使用梯度的两次分水岭分割，从结果可以看出还存在过分割问题（在方法1的基础上改进）h=fspecial('sobel');%获得纵方向的sobel算子fd=double(f);g=sqrt(imfilter(fd,h,'replicate').^2+imfilter(fd,h','replicate').^2);%使用sobel算子进行梯度运算l=watershed(g);%分水岭运算wr=l==0;g2=imclose(imopen(g,ones(3,3)),ones(3,3));%进行开闭运算对图像进行平滑l2=watershed(g2);%再次进行分水岭运算wr2=l2==0;f2=f;f2(wr2)=255;figuresubplot(2,3,1),imshow(f);subplot(2,3,2),imshow(g);subplot(2,3,3),imshow(l);subplot(2,3,4),imshow(g2);subplot(2,3,5),imshow(l2);subplot(2,3,6),imshow(f2);%方法3：使用梯度加掩模的三次分水岭算法（在方法2的基础上改进）h=fspecial('sobel');%获得纵方向的sobel算子fd=double(f);g=sqrt(imfilter(fd,h,'replicate').^2+imfilter(fd,h','replicate').^2);%使用sobel算子进行梯度运算l=watershed(g);%分水岭运算wr=l==0;rm=imregionalmin(g); %计算图像的区域最小值定位，该函数仅仅是用来观察为何分水岭算法产生这么多集水盆地im=imextendedmin(f,2);%上面仅是产生最小值点，而该函数则是得到最小值附近的区域，此处的附近是相差2的区域fim=f;fim(im)=175; %将im在原图上标识出，用以观察lim=watershed(bwdist(im));%再次分水岭计算em=lim==0;g2=imimposemin(g,im|em);%在梯度图上标出im和em，im是集水盆地的中心，em是分水岭l2=watershed(g2); %第三次分水岭计算f2=f;f2(l2==0)=255; %从原图对分水岭进行观察figuresubplot(3,3,1),imshow(f);subplot(3,3,2),imshow(g);subplot(3,3,3),imshow(l);subplot(3,3,4),imshow(im);subplot(3,3,5),imshow(fim);subplot(3,3,6),imshow(lim);subplot(3,3,7),imshow(g2);subplot(3,3,8),imshow(l2)subplot(3,3,9),imshow(f2);。

• 过分割现象： 对微弱边缘具有良好的响应，图像中的噪 声、物体表面细微的灰度变化，都会产生过度分割的现象；
• 为消除分水岭算法产生的过度分割，通常可以采用两种处 理方法： 一是利用先验知识去除无关边缘信息。 二是修改梯度函数使得集水盆只响应想要探测的目标。
3. Matlab演示
• 代码： • clear; close all; clc; • rgb = imread('forest.png'); • • f = rgb2gray( rgb ); • figure(1); • imshow(rgb); • title('原始图像'); • • fgm = imregionalmax(f); • D = bwdist(fgm);%¼ÆËã¾àÀë • DL = watershed(D);%·ÖË®Áë±ä»» • bgm = DL == 0;%ÇóÈ¡·Ö¸î±ß½ç • f0 = f; • f0(bgm) = 255; • • figure(2); • imshow(f0); • title('»ùÓÚ¾àÀë±ä»»µÄ·ÖË®Áë·Ö¸î');
• b. 为得到图像的边缘信息，通常把梯度图像作为输入图像 进行处理。
分水岭脊线
汇水盆地
a
b
c
1. a中红色箭头指示区域为谷底，代表低亮度像素；黄色 箭头所示为山脊，代表高亮度像素；
2. b中灰色部分表示水从谷底逐渐涨高后的状态； 3. C中表示水面到达一定程度后留下的分水岭（最高点）
3. 不足
• f1 = f;
• f1(wr) = 255;
•
• figure(3);
• imshow(f1);
• title('»ùÓÚÌݶȵķÖË®Áë·Ö¸î');

解决分水岭算法的过分割问题班级：020751学号：02075087姓名：刘恺摘要针对基于分水岭变换的分割算法通常存在过分割现象，提出了一种新的分割算法，采用形态学的运算去除噪声及背景像素的影响，搜索区域极大值点，将分割定位于目标图像，从而达到很好的分割效果，方法从消除过分割及区域轮廓定位等方面均具有很好的分割效果。

关检词图像分割,分水岭变换,数学形态学Abstract The article is based on watershed algorithm, proposed a method of image segmentation, adopted the morphology arithmetic to eliminate the effect of noise and background pixel, search for the max point in each area, let segmentation orientate as target image, could reach very good segment effect. The method can efficiently eliminate over-segmentation, and hold the position of region contours without evident bias.Key words image segmentation, watershed transform ,mathematical morphology1.1图像分割综述把图像分解为一些特定的性质相似的部分（区域或对象），并用这些部分对图像进行分析和描述。

一幅图像往往包含许多不同类型的区域，如物体、环境和背景等。

图像分析的一个重要方法就是用它们作为基本组成成分对图像进行描述。

例如为了在气泡室图片中检出质点碰撞形式并判定其发生位置，就要在图像中分割出气泡的轨迹及其端点。

基本概念一点通从理论上讲，图像是一种二维的连续函数，然而在计算机上对图像进行数字处理的时候，首先必须对其在空间和亮度上进行数字化，这就是图像的采样和量化的过程。

空间坐标（x,y）的数字化称为图像采样，而幅值数字化称为灰度级量化。

对一幅图像采样时，若每行（横向）采样数为M，每列（纵向）采样数为N，则图像大小为M*N个像素，f(x,y)表示点(x,y) 处的灰度值，则F(x,y)构成一个M*N 实数矩阵****************************经验分享：“像素”的英文为“pixel”，它是“picture”和“element”的合成词，表示图像元素的意思。

我们可以对“像素”进行如下理解：像素是一个面积概念，是构成数字图像的最小单位。

****************************把采样后所得的各像素灰度值从模拟量到离散量的转换称为图像灰度的量化。

量化是对图像幅度坐标的离散化，它决定了图像的幅度分辨率。

量化的方法包括：分层量化、均匀量化和非均匀量化。

分层量化是把每一个离散样本的连续灰度值只分成有限多的层次；均匀量化是把原图像灰度层次从最暗至最亮均匀分为有限个层次，如果采用不均匀分层就称为非均匀量化。

当图像的采样点数一定时，采用不同量化级数的图像质量不一样。

量化级数越多，图像质量越好；量化级数越少，图像质量越差。

量化级数小的极端情况就是二值图像。

****************************经验分享:“灰度”可以认为是图像色彩亮度的深浅。

图像所能够展现的灰度级越多，也就意味着图像可以表现更强的色彩层次。

如果把黑——灰——白连续变化的灰度值量化为256个灰度级，灰度值的范围为0～255，表示亮度从深到浅，对应图像中的颜色为从黑到白。

****************************因此，对数字图像进行处理，也就是对特定的矩阵进行处理。

在C语言中，对M×N数字图像处理的核心代码如下：for (j=1;j<N+1;j++)for(i=1;i<M+1;i++)｛对I(i,j)的具体运算｝；在Matlab中，对M×N数字图像处理的核心代码如下：for i=1:Nfor j=1:M对I(i,j)的具体运算endend一幅数字图像可以用一个矩阵来表示，对数字图像进行处理，实质上就是对特定的图像矩阵进行变换的过程，因此，图像变换是数字图像处理技术的基础。

下标L表示左,R表示右,T表示上,B表示下,abs表示取绝对值
min(max(abs(R- RT), abs(G-GT), abs(B-BT)),max(abs(R- RB), abs(G-GB), abs(B-BB)),max(abs(R- RL), abs(G-GL), abs(B-BL)),max(abs(R-R R), abs(G-GR), abs(B-BR)))
二、传统分水岭算法
传统的分水岭分割方法,其基本思想是把图像看作是测地学上的拓扑地貌,图 像中每1像素的灰度值表示该点的海拔高度,每1个局部极小值及其影响区域 称为集水盆地,而集水盆地的边界则形成分水岭.基于梯度图像的直接分水岭 算法容易导致图像的过分割,产生这1现象的原因主要是由于输入的图像存在 噪声等而产生许多小的集水盆地,从而导致分割后的图像不能将图像中有意 义的区域表示出来.所以必须对分割结果的相似区域进行合并.
相应的队列. 如果这个灰度上的队列处理完了,就继续找下1个非空队列.
注 意 ： 第 1轮 ,把标 记点的 邻居点 放入相 应的优 先级队 列后,先 进先出 的原则 处理队 列中的 像素结 点,找到 1个非 零结点 后,执行 第1,2,3步 ,执行 完第3步 之后 ,重新更 新队列 再次进 行扫描 .
1、有标的分水岭算法 1.准备好原图和掩模图
2.对掩模图做初始化标记,以形成最初的注水区域,设置mask边框值为-1,即每个标记 （种子,全为正值,1,2,3...）都是1个初始聚水盆,标记的周围1圈的邻居像素就是 聚水盆的初始边界.
3.在mask图像中找邻居像素（该像素四邻域内有标记点）,并将邻居像素对应 原图中的点放入相应的优先级队列
优先级队列
Y
0 1 2 3 4 5 6

水系提取算法（D8）的matlab 实现D8算法是当今非常成熟的提取水系（或分水岭）的计算机实现方法。

这里笔者结合自身的编程实践介绍D8算法的matlab 实现过程，谨与大家分享。

D8算法分为两部分实现：每个栅格点水流方向的计算；每个栅格点汇水面积的计算。

1、水流方向的计算在水流方向的计算中，本人结合matlab 内嵌的滤波工具，利用一个简单的非线性滤波来实现，具体内容包括一个自己编辑的确定水流方向的函数flowdirection 和若干脚本命令，如下：以下是自己编辑的flowdirection 函数代码：function output=flowdirection(a)n=size(a);for i=1:n(2) k=0; b=-inf; for j=[1:4,6:9]if rem(j,2)==0r(j)=a(5,i)-a(j,i);elser(j)=(a(5,i)-a(j,i))/sqrt(2);endif r(j)>bb=r(j);k=j;endendoutput(i)=k;end执行的脚本代码如下：>> uiopen('F:\课件\2009田淑芳\正射校正\DEM.tif',1)%打开DEM 高程数据，生成的数据矩阵名可自行定义，这里默认为DEM>>DEM=mat2gray(DEM);%高程数据归一化处理>>DEM=padarray(DEM,[1 1],'replicate');%对数据边缘进行自动填充>>direc8=colfilt(DEM,[3 3],'sliding',@flowdirection);%执行非线性滤波，得到方向矩阵，得到的值分别为{1 ,2,3,4,6,7,8,9}.其方向意义如上图矩阵所示，如1代表北西向，8代表正东1、汇水面积的计算这里笔者根据自己的编程实践经验，给出一个函数来计算不同窗口大小下汇水面积的大小。

matlab中分水岭算法的原理English:The watershed algorithm is a segmentation technique that is used to separate touching or overlapping objects in an image. It is based on the concept of a topographic surface, where the pixel intensities are interpreted as the elevation of the surface. The algorithm begins by identifying the regional minima in the image, which are considered as the markers for the different objects. Then, the algorithm simulates a flooding process, where the elevated regions (or catchment basins) are gradually filled with water until they merge at the regional minima. This process creates a set of boundaries that separate the different catchment basins, resulting in the segmentation of the image. The watershed algorithm is particularly useful for segmenting complex and irregular objects, as it is able to find boundaries based on both intensity and spatial information.Translated content:分水岭算法是一种用于分割图像中接触或重叠对象的分割技术。

MATLAB程序设计实验报告院（系）名称宇航学院专业名称图像处理与模式识别学生学号13151023学生姓名荣楚君2016年5月实验基于Matlab水域分割的图像分割实验一、实验目的1、掌握Matlab图像处理工具箱的使用。

2、学习使用联机帮助、Demo与查找更多的Matlab功能。

3、熟悉使用Matlab进行交互操作的方法。

4、学习图像分割的基本知识。

二、实验要求（一）、对实验过程的要求1、编写M-文件，实现给定图像的分割。

2、学习Matlab中Demo的相关帮助。

3、实验中生成的中间结果和数据尽量保存。

（二）、对实验报告的撰写要求1、参考附录的实验报告格式样本撰写。

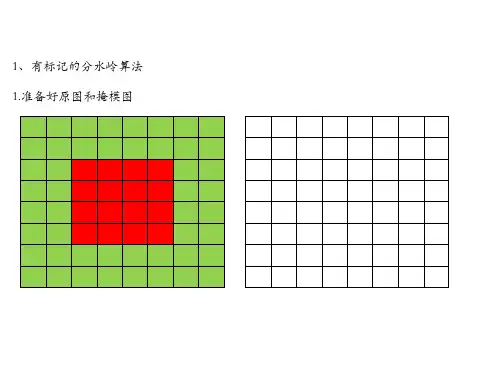
2、“实验结果”主要包括：（1）基于标记的和非标记的两种水域分割结果图。

（2）用于水域分割的Marker图。

（3）将水域分割得到结果的轮廓在原图上显示出来。

3、实验报告附录中包含M-文件的源代码，要注意代码的格式。

三、实验环境和设备1、PC机，Windows XP / 7操作系统。

2、MatlabR2010及其以上版本。

四、实验原理1、图像分割图像分割就是把图像分成若干个特定的、具有独特性质的区域并提出感兴趣目标的技术和过程，它是由图像处理到图像分析的关键步骤。

图像分割的关键是将前景与背景区分开。

分水岭算法又称为水域分割，是一种基于拓扑理论的数学形态学的分割方法，其基本思想是把图像看作是测地学上的拓扑地貌，图像中每一点像素的灰度值表示该点的海拔高度，每一个局部极小值及其影响区域称为集水盆，而集水盆的边界则形成分水岭。

分水岭的概念和形成可以通过模拟浸入过程来说明。

在每一个局部极小值表面，刺穿一个小孔，然后把整个模型慢慢浸入水中，随着浸入的加深，每一个局部极小值的影响域慢慢向外扩展，在两个集水盆汇合处构筑大坝，即形成分水岭。

水域分割一般是在梯度图像上实现，梯度图上的局部极小值一般代表较平滑的区域，即为目标中心区域或者变化不大的背景区域，集水形成的“分水岭”则位于梯度较大的边缘区域。

matlab 分割三维模型算法一、引言三维模型分割是计算机视觉领域的一个重要问题，它在三维建模、物体识别、医学图像分析等领域都有广泛的应用。

在matlab中，有多种方法可以实现三维模型分割，其中最常见的是基于图像分割算法和深度学习算法。

本文将主要介绍基于图像分割算法的matlab三维模型分割方法。

二、matlab三维模型分割算法1. 基于区域生长的三维模型分割算法区域生长是一种基于相似度测量的图像分割技术，它可以将相邻像素点合并成为一个区域。

在三维模型中，区域生长可以被用来将同一部位的点聚合成为一个整体。

具体实现步骤如下：（1）选取种子点：首先需要选取一个或多个种子点作为起始点。

（2）定义相似度测量标准：根据实际情况定义相似度测量标准。

（3）寻找邻居：以种子点为中心，在周围搜索与之相似的点。

（4）加入到当前区域：如果找到了符合条件的点，则将其加入到当前区域中。

（5）重复上述步骤：不断重复上述步骤，直到不能再添加新的点为止。

2. 基于分水岭算法的三维模型分割算法分水岭算法是一种基于图像梯度的分割技术，它可以将图像中的每个像素点标记为前景或背景。

在三维模型中，分水岭算法可以被用来将不同部位的点分离开来。

具体实现步骤如下：（1）计算梯度：首先需要计算出三维模型中每个像素点的梯度值。

（2）标记种子点：根据需要进行标记，例如将某些像素点标记为前景或背景。

（3）生成高斯金字塔：为了减少计算量，需要对三维模型进行高斯金字塔处理。

（4）生成距离变换图：根据梯度值和种子点位置生成距离变换图。

（5）应用分水岭算法：根据距离变换图应用分水岭算法进行分割。

3. 基于聚类的三维模型分割算法聚类是一种基于相似性度量的数据分类方法，它可以将数据集中相似的数据归为一类。

在三维模型中，聚类可以被用来将同一部位的点聚合成为一个整体。

具体实现步骤如下：（1）选取特征：首先需要选取合适的特征来描述三维模型中的点。

（2）定义相似度测量标准：根据实际情况定义相似度测量标准。

基于分水岭分割算法
分水岭分割算法是一种常用的图像分割算法，也称为基于区域的分割算法。

它基于图像中不同区域的灰度差异，通过将图像看作是一幅地形图，将图像中的每个像素视为地形上的一个点，通过计算该点的梯度来确定其高度。

然后，根据图像的高度差异将图像分割成多个不同的区域。

分水岭分割算法的主要思想是首先将图像中的每个像素看作是一个水滴，并将水滴放在图像中的极小值点上。

然后根据像素之间的连通性以及梯度信息，逐步合并水滴，最终得到图像的分割结果。

算法步骤如下：
1. 预处理：对图像进行去噪处理，例如使用高斯滤波器。

2. 计算梯度：计算图像中每个像素的梯度值，一般使用Sobel
算子或Laplacian算子。

3. 标记种子点：根据梯度信息找到图像中的极小值点，并将这些点作为种子点。

4. 标记像素：通过种子点进行扩张，将每个像素标记为其所属的种子点。

5. 构建水流线：将图像中未标记的像素分配到最近的种子点，形成水流线。

6. 汇合水流线：当水流线汇合时，形成边界，将水流线连接到其最近的汇合点。

7. 分割图像：根据水流线和汇合点，将图像分割成多个不同的区域。

分水岭分割算法能够有效地处理图像中的多个前景物体以及复杂背景，但在一些情况下可能会出现过分割或欠分割的问题，需要根据具体应用场景进行调优和改进。

在MATLAB中，可以使用`watershed`函数来实现分水岭算法。

以下是一个简单的示例代码：
```matlab
读取图像
f = imread('image.png');
转换为灰度图像
if size(f, 3) == 3
f = rgb2gray(f);
end
二值化图像
b = im2bw(f, graythresh(f));
计算图像的距离变换
d = bwdist(b);
应用分水岭算法
l = watershed(-d);
提取边缘
w = l == 0;
从二值图像中提取感兴趣的区域
g = b & ~w;
```
在这个示例中，我们首先读取一张图像，并将其转换为灰度图像。

然后，我们使用`im2bw`函数和`graythresh`函数将图像二值化。

接下来，我们计算图像的距离变换，并使用`watershed`函数应用分水岭算法。

最后，我们使用一个简单的逻辑运算从二值图像中提取感兴趣的区域。

/*====================================================================函数名： Watershed功能：用标记-分水岭算法对输入图像进行分割算法实现：无输入参数说明： OriginalImage --输入图像（灰度图，0~255）SeedImage --标记图像（二值图，0-非标记，1-标记）LabelImage --输出图像（1-第一个分割区域，2-第二个分割区域，...）row --图像行数col --图像列数返回值说明：无====================================================================*/void WINAPI CDib::Watershed(unsigned char **OriginalImage, char** SeedImage, int **LabelImage, int row, int col){// using namespace std;//标记区域标识号，从1开始int Num=0;int i,j;//保存每个队列种子个数的数组vector<int*> SeedCounts;//临时种子队列queue<POINT> quetem;//保存所有标记区域种子队列的数组，里面放的是种子队列的指针vector<queue<POINT>*> vque;int* array;//指向种子队列的指针queue<POINT> *pque;POINT temp;for(i=0;i<row;i++){for(j=0;j<col;j++)LabelImage[i][j]=0;}int m,n,k=0;BOOL up,down,right,left,upleft,upright,downleft,downright;//8 directions...//预处理,提取区分每个标记区域，并初始化每个标记的种子队列//种子是指标记区域边缘的点，他们可以在水位上升时向外淹没（或者说生长）//pan's words：我的理解是梯度值较小的象素点，或者是极小灰度值的点。

第三部分实习题目实习一用鼠标进行交互式绘图【实习内容】面向对象的分析与设计，学习用消息机制（或事件机制）响应用户的请求，学习高级语言的绘图操作，掌握图形中点、线的属性，开发工具的使用。

【基本要求】用鼠标在窗口内任意绘图；能绘制直线、矩形、椭圆、多边形等，能对封闭图形进行填充，可交互式选择线的形状、线的粗细、线的颜色、填充的颜色；能实现所绘图形的保存和打开及显示。

【较高要求】能实现图形编辑的无级Undo与Redo功能。

【测试数据】不需要。

【实现提示】线对象由许多点对象的组成，可用模板（对象数组或指向对象的指针数组）实现图形数据的保存。

Undo与Redo功能可仿照实习报告范例中图象编辑示例程序用设计模式实现。

【实习报告写作重点】1.数据结构设计（线对象有哪些属性？多个线对象怎样保存，线对象怎样用点对象描述）2.类的设计，用UML描述类的静态视图和交互视图，特别是文档类（保存数据的类）和视图类（显示数据的类）的关系。

（可用Microsoft Visio画图）3.小结（已实现了哪些功能？以后哪些方面需要加强？）。

如果你使用了设计模式，试说明使用设计模式的优点。

实习二三维建模【实习内容】面向对象的分析与设计，计算机图形学，三维图形开发工具。

【基本要求】建立简单的三维物体(长方体、圆柱体、球体、四面体等)，将其平行投影至XY、XZ、YZ平面( 沿轴方向)上，通过鼠标在此三个平面上交互编辑物体，并画出物体的透视投影图(投影中心、投影方向、投影平面自定)。

【较高要求】能用鼠标交互式绘制，又能根据参数绘制。

能用基本的图形组成复杂的图形。

【测试数据】不需要。

【实现提示】推荐使用Visual C++ 和OpenGL或DirectX.；。

【实习报告写作重点】1.需求分析2. OPENGL或DIRECTX的基本功能和特征，你使用了其中哪些功能？3.小结（已实现了哪些功能？以后哪些方面需要加强？）实习三函数曲线和曲面的绘制【实习内容】面向对象的分析与设计，计算机图形学，高级语言图形绘制。

分水岭算法的详细介绍（附c代码）转所谓分水岭算法有好多种实现算法，拓扑学，形态学，浸水模拟和降水模拟等方式。

要搞懂就不容易了。

Watershed Algorithm(分水岭算法)，顾名思义，就是根据分水岭的构成来考虑图像的分割。

现实中我们可以或者说可以想象有山有湖的景象，那么那一定是水绕山，山围水的情形。

当然在需要的时候，要人工构筑分水岭，以防集水盆之间的互相穿透。

而区分高山（plateaus）与水的界线，以及湖与湖之间的间隔或都是连通的关系，就是我们可爱的分水岭（watershed）。

为了得到一个相对集中的集水盆，那么让水涨到都接近周围的最高的山顶就可以了，再涨就要漏水到邻居了，而邻居，嘿嘿，水质不同诶，会混淆自我的。

那么这样的话，我们就可以用来获取边界灰阶大，中间灰阶小的物体区域了，它就是集水盆。

浸水法，就是先通过一个适当小的阈值得到起点，即集水盆的底；然后是向周围淹没也就是浸水的过程，直到得到分水岭。

当然如果我们要一直淹没到山顶，即是一直处理到图像灰阶最高片，那么，当中就会出现筑坝的情况，不同的集水盆在这里想相遇了，我们要洁身自爱，到这里为止，因为都碰到边界了；那么即使在相遇时没有碰到最高灰阶的地方，也需要人工构筑分水岭，区分不同的区域。

不再上山。

构筑属于自己的分水岭在计算机图形学中，可利用灰度表征地貌高。

图像中我们可以利用灰度高与地貌高的相似性来研究图像的灰度在空间上的变化。

这是空域分析，比如还可以通过各种形式的梯度计算以得到算法的输入，进行浸水处理。

分水岭具有很强的边缘检测能力，对微弱的边缘也有较好的效果。

这与分水岭扩张的阈值的设置有关系，阈值可以决定集水盆扩张的范围。

但自我构筑的能力却不受影响。

为会么这么说呢？为什么有很强的边缘检测能力，而又能得到相对集中的连通的集水盆？现实中很好办，我们在往凹地加水的时候，直到它涨到这一块紧凑的山岭边缘就不加了；但是如果有一条小山沟存在，那没办法，在初始阈值分割的时候，也就是山沟与集水盆有同样的极小值，而且它们之间是以这个高度一直连接的。