汽液平衡数据的测定及数据处理

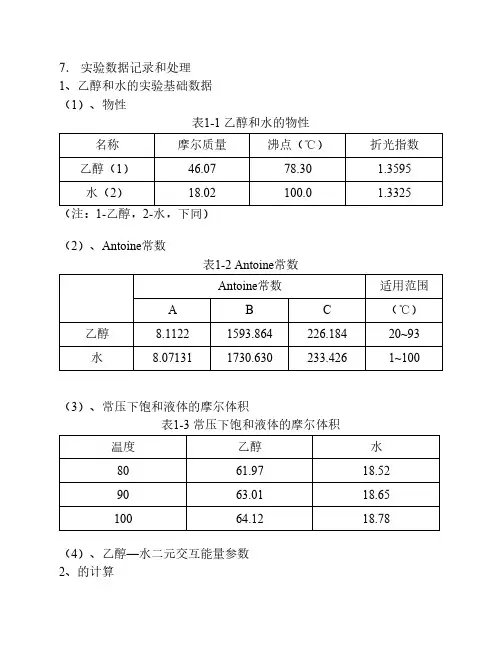
7．实验数据记录和处理1、乙醇和水的实验基础数据（1）、物性表1-1 乙醇和水的物性名称摩尔质量沸点（℃）折光指数乙醇（1）46.0778.30 1.3595水（2）18.02100.0 1.3325（注：1-乙醇，2-水，下同）（2）、Antoine常数表1-2 Antoine常数Antoine常数适用范围A B C（℃）乙醇8.11221593.864226.18420~93水8.071311730.630233.4261~100（3）、常压下饱和液体的摩尔体积表1-3 常压下饱和液体的摩尔体积温度乙醇水8061.9718.529063.0118.6510064.1218.78（4）、乙醇—水二元交互能量参数2、的计算（1）、内插法平衡温度下乙醇和水的摩尔体积根据表1-3数据，利用内插法求得平衡温度下的摩尔体积，列表如下。

表1-4平衡温度下乙醇和水的摩尔体积（常压下）温度（℃）乙醇的摩尔体()水的摩尔体积()90.263.0318.6585.662.5518.5983.262.3018.5682.362.2118.55以1#数据为计算示例。

（下同）（2）、Willson配偶参数的确定根据表1-4计算Willson配偶参数，计算结果如列表所示。

表1-5 平衡温度下的Willson配偶参数温度（℃）90.20.21770.850685.60.21740.825983.20.21750.816182.30.21750.8125（3）、Willson方程计算。

由表1-5和原始数据根据Willson方程计算，计算结果如下表所示。

表1-6 平衡温度下乙醇—水的温度（℃）乙醇水90.2 4.0882 1.005385.6 3.2201 1.023683.2 2.6358 1.051582.3 1.9939 1.12023、、的计算（1）、平衡温度下的饱和蒸汽压Antoine公式：根据表1-2数据和Antoine公式计算纯组分在平衡温度下的饱和蒸汽压，计算结果如下表所示。

实验二二元气液平衡数据的测定一、实验目的1.测定苯一正庚烷二元体系在常压下的气液平衡数据。

2.通过实验了解平衡釜的结构，掌握气液平衡数据的测定方法和技能。

3 .应用Wilson方程关联实验数据。

二、实验原理气液平衡数据是化学工业发展新产品、开发新工艺、减少能耗、进行三废处理的重要基础数据之一。

化工生产中的蒸馏和吸收等分离过程设备的改造与设计、挖潜与革新以及对最佳工艺条件的选择，都需要精确可靠的气液平衡数据。

这是因为化工生产过程都要涉及相间的物质传递，故这种数据的重要性是显而易见的。

随着化工生产的不断发展，现有气液平衡数据远不能满足需要。

许多物系的平衡数据，很难由理论直接计算得到，必须由实验测定。

平衡数据实验测定方法有两类，即间接法和直接法。

直接法中又有静态法、流动法和循环法等。

其中循环法应用最为广泛。

若要测得准确的气液平衡数据，平衡釜是关键。

现已采用的平衡釜形式有多种，而且各有特点，应根据待测物系的特征，选择适当的釜型。

用常规的平衡釜测定平衡数据，需样品量多，测定时间长。

本实验用的小型平衡釜主要特点是釜外有真空夹套保温，釜内液体和气体分别形成循环系统，可观察釜内的实验现象，且样品用量少，达到平衡速度快，因而实验时间短。

以循环法测定气液平衡数据的平衡釜类型虽多，但基本原理相同，如图1所示。

当体系达到平衡时，两个容器的组成不随时间变化，这时从A和B两容器中取样分析，即可得到一组平衡数据。

图1平衡法测定气液平衡原理图当达到平衡时，除了两相的压力和温度分别相等外，每一组分的化学位也相等，即逸度相等，其热力学基本关系为：#=疗 (1)如py】=、］『国常压下，气相可视为理想气体，电=1；再忽略压力对液体逸度的影响，f=po从而得出低压下气液平衡关系式为：py\ = .......... ⑵式中，P——体系压力（总压）；—纯组分i在平衡温度下饱和蒸气压，可用安托尼^Antoine）公式计算;覆、力——分别为组分i在液相和气相中的摩尔分率；——组分I的活度系数口由实验测得等压下气液平衡数据，则可用：计算出不同组成下的活度系数。

气液相平衡实验报告实验目的：探究气液相平衡的基本规律和影响因素。

实验器材：1. 恒温水浴槽2. U型玻璃管3. 气压计4. 液体试剂5. 多孔瓷芯6. 温度计7. 固体试样实验原理：气液相平衡是指在一定温度下，气体和液体之间达到平衡状态的现象。

实验中，使用U型玻璃管连接液体试剂和气压计，通过控制温度和将气态和液态物质接触，观察两相之间达到平衡时的气体压力，并推断出气液相平衡的规律。

实验步骤：1. 准备实验器材，搭建实验装置。

2. 将恒温水浴槽加热至设定温度。

3. 将液体试剂注入U型玻璃管中，保证一浸没在水中，另一端露出水面。

4. 预热液体试剂至与水浴槽温度相同。

5. 打开气压计的阀门，使其与U型玻璃管内的气体接触。

6. 观察并记录气压计读数，并等待数分钟使气液平衡达到稳定。

7. 将温度计插入水浴槽，记录水浴温度。

8. 重复以上步骤，分别在不同温度和液体试剂条件下进行多次实验。

实验结果与讨论：1. 实验结果将以表格的形式呈现，记录每次实验所得的气体压力和温度数据。

2. 根据实验数据，绘制气体压力与温度之间的图像。

3. 分析图像中的趋势，推导气液相平衡的规律。

4. 探讨温度、压力和液体性质对气液相平衡的影响。

结论：通过本实验，我们得出了气液相平衡的实验数据，并绘制出相应的图像，从图像中可以看出，随着温度的升高，气体压力也相应增加。

这说明在一定温度下，气体的压强与温度呈正相关关系。

实验还发现，不同的液体试剂在相同温度下存在着不同的气压计读数，提示不同的液体试剂在气液相平衡中具有不同的特性。

我们的实验结果验证了气液相平衡的规律，为进一步研究和应用气液相平衡的相关领域提供了实验依据和理论支持。

附注：本实验只给出了基本实验步骤和结果讨论，详细的数据和图像以及进一步的分析可参考实验记录表和附件中的实验数据。

实验数据处理（1） 乙醇浓度的计算利用实验参考书提供的乙醇标准曲线数据，由折光率和乙醇摩尔百分率关系用内插法得到乙醇摩尔分率如表1. 计算示例：以第一组气相为例第一组的气相折光率为1.3595落在折光率1.3594-1.3599之间，对应的乙醇摩尔分率为0.9379-0.8810.插值法计算如下：1.3599−1.35950.8810−x =1.3599−1.35940.8810−0.9379解出x=0.9265,水的气相摩尔分率=1-x-=0.0735.（2） 温度计暴露温度校正n=t 观-（50-1.6*6.7），t 室=25℃，t 实际=t 观+0.00016n(t 观-t 室)；tp=t 实际+0.000125（t 室+273）（P-760），因为本小组实验的P 大于标准大气压，所以用P-760。

计算示例：以第一组为例；n=t 观-39.28=77.81-39.28=38.53，t 实际=77.81+0.00016*38.53*（77.81-25）=78.14℃ 平衡温度计算：tp=t 实际+0.000125（t 室+273）（P-760）=78.18+0.000125(25+273)(761.313-760)=78.19℃（3） 实验测得的温度和压强以及摩尔分率如表1、表二。

（4） 由所得的二元气液平衡数据表记录如表二。

活度计算示例：以第一组气相为例根据安托尼(Antoine)公式，lg(Ps)=A-B/(C + t/℃)，求出不同平衡温度下乙醇和水的饱和气压，乙醇的安托尼(Antoine)参数:A=8.21330,B=1652.050,C=231.480,水的安托尼(Antoine)参数：A=7.96681,B=1668.21,C=228。

计算乙醇的饱和蒸汽压：lgP=8.2133-1652.05/(231.48+78.19)，得P=755.879mmHg; 计算水的饱和蒸汽压：lgP=7.96681-1668.21/(228+78.19)，得P=330.029mmHg; 计算活度系数： 由简化后的公式：0i p x py i ii =γ 乙醇的活度系数：γA=(P*yA)/(xA*P0)=(761.313*0.9265)/(0.8718*755.879)=1.0704水的活度系数：γB=(P*yB)/(xB*P0)=(761.313*0.0735)/(0.1282*330.029)=1.3225（5） 由二元气液平衡数据绘制的相图如图2。

二组分气液平衡相图实验报告实验目的，通过实验，掌握二组分气液平衡相图的测定方法和实验技术。

实验原理，在一定温度下，将两种组分的混合物置于容器中，通过调节温度和压力，观察和记录气液相变的情况，最终绘制出气液平衡相图。

实验仪器，实验中所用的仪器有压力计、温度计、气液平衡相图测定装置等。

实验步骤：
1. 将两种组分混合物置于气液平衡相图测定装置中，调节温度和压力；
2. 观察和记录气液相变的情况，包括气液相变的压力和温度值；
3. 根据记录的数据，绘制出气液平衡相图。

实验结果与分析：
通过实验测定和数据处理，得到了二组分气液平衡相图。

在图中，我们可以清晰地看到气相和液相的边界，以及气液相变的压力和温度值。

根据相图的形状和数据分析，我们可以得出一些结论和规律。

实验结论：
1. 随着温度的升高，气相区域逐渐扩大，液相区域逐渐缩小；
2. 随着压力的升高，气相区域逐渐扩大，液相区域逐渐缩小；
3. 在一定温度下，压力越大，气相区域越大，液相区域越小；
4. 在一定压力下，温度越高，气相区域越大，液相区域越小。

实验总结：
通过本次实验，我们掌握了二组分气液平衡相图的测定方法和实验技术，了解了气液相变的规律和特点。

同时，也加深了对相图的理解和应用，为今后的实验和研究工作打下了坚实的基础。

结语：
二组分气液平衡相图实验是化学实验中的重要内容，通过本次实验，我们不仅学会了实验操作技巧，更重要的是对气液平衡相图有了更深入的理解。

希望通过今后的学习和实践，能够更好地运用这些知识，为科学研究和工程应用做出贡献。

序号：40化工原理实验报告实验名称：二元系统气液平衡数据测定学院：化学工程学院专业：化学工程与工艺班级：化工095班姓名：何小龙学号 0940201051 同组者姓名：杨飞黄云张阳指导教师：周国权日期： 2012年3月29日一、实验目的1．了解和掌握用双循环汽液平衡器测定二元系统汽液平衡数据的方法。

2．了解缔合系统汽液平衡数据的关联方法，从实验测得的T-p-x-y数据计算个组分的活度系数。

3．通过实验了解平衡釜的构造，掌握汽液平衡数据的测定方法和技能。

4．掌握二元系统平衡相图的绘制。

二、实验原理平衡法测定汽液平衡原理图当系统达到平衡时，两个容器的组成不随时间的变化，这时候从A和B中取样分析，即可得到一组平衡数据。

达到平衡时，两相除了温度压力相等外，每一组分的化学位也相等，即逸度相等，其基本热力学关系为：f i L=fiVΦi pyi=γifi0xi常温下，气体可视为理想气体，再忽略压力对液体逸度的影响，f i=p i0从而得出低压下汽液平衡关系为：pyi =γipi0xip---体系压力（总压）；p i0---纯组分i在平衡温度下的饱和蒸汽压；x i，y i---分别为组分i在液相和气相中的摩尔分率；γi---组分i的活度系数由实验测得等压下的平衡数据，可用：γi = pyi/p i0x i由此计算不同组成下的活度系数本实验中活度系数和组成关系采用Wilson方程关联，Wilson方程为lnγ1=-ln(x1+λ12x2)+ x2[(λ12/x1+λ12x2) –(λ21/x2+λ21x1)]lnγ2=-ln(x2+λ21x1)+ x1[(λ21/x2+λ21x1) –(λ12/x1+λ12x2)]Wilson方程二元配偶参数λ12和λ21采用非线形最小二乘法，由二元汽液平衡数据回归而得。

目标函数选为气相组成误差的平方和，即：F=Σj=1m(y1实-y1计)2j+( y2实-y2计)2j三、实验装置与试剂1.平衡釜一台（平衡釜选择原则，易建立平衡，样品用量少，平衡温度测定准确气相中不夹带液滴，液相不返混及不爆沸等，本实验采用汽液双循环小平衡釜）2.阿贝折射仪一台3.温度计4.1ml及5ml的注射器若干四、实验步骤及注意事项1.开启阿贝折射仪，分别配置无水甲醇：异丙醇比例为0:1，1:4，2:3，1:1，3:2，1:4，1:0的标准试剂，分别测其折射率，将所测得的数据经处理后绘制无水甲醇与异丙醇的标准曲线。

二元系统气液平衡数据测定实验报告实验目的：1. 了解气相和液相的特性和平衡状态；2. 熟悉使用实验仪器进行二元系统气液平衡数据测定；3. 掌握气液平衡实验的数据处理方法。

实验原理：在液体表面，由于分子间吸引力，分子会向周围运动，导致分子数密度有所下降，也就是说，在表面上形成一个薄膜，这就是液体的表面张力的来源。

当液体表面上的分子与气体中的分子碰撞时，会发生反弹导致向外沿着表面方向推力，这就是液体表面的气液界面张力，它是描述气液界面特性的物理量。

气液界面上的分子密度不均匀，会导致气相和液相之间的交换。

在一种给定的温度下，当气相和液相之间的交换达到一定的平衡状态时，称为气液平衡。

在这种状态下，气相和液相的分子数密度不再发生明显的变化。

通过气液平衡实验，可以测定气液界面张力和液体和气体之间的平衡常数，从而获得二元系统气液平衡的数据。

实验仪器：1. 二元系统气液平衡实验仪器；2. 水、乙醇等液体样品；3. 高钼酸钠、酚酞等试剂。

实验步骤：1. 清洗实验仪器：将实验仪器中的气路及液路中的管道和阀门进行清洗，保证实验测量时的通气畅通和样品无杂质。

2. 调整实验仪器：将待测液体注入样品瓶中，打开气路和液路中的阀门，进行预热和抽气，直至达到平衡状态。

3. 测量实验数据：通过测定不同温度下的液体和气体的平衡常数，获得二元系统气液平衡的数据。

4. 处理数据：将实验数据进行整理分析，得出二元系统气液平衡的相关参数。

实验结果：通过实验测量，得出了二元系统气液平衡的相关数据，具体如下：1. 温度：25℃液体样品：水气体样品：空气气液界面张力：72.2 mN/m液体与气体间的平衡常数：0.872. 温度：30℃液体样品：乙醇气体样品：空气气液界面张力：28.6 mN/m液体与气体间的平衡常数：0.65实验结论：通过本次实验的测量和分析，得出了二元系统气液平衡的相关参数。

在不同的温度下，不同的液体和气体之间会发生不同程度的平衡，液体之间和气体之间的分子密度也不同。

实验二化学吸收系统气液平衡数据的测定A 实验目的化学吸收是工业气体净化和回收常用的方法，为了从合成氨原料气、天然气、热电厂尾气、石灰窑尾气等工业气体中脱除CO2 、H2S、SO2等酸性气体，各种催化热钾碱吸收法和有机胺溶液吸收法被广泛采用。

在化学吸收过程的开发中，相平衡数据的测定必不可少，因为它是工艺计算和设备设计的重要基础数据。

由于在这类系统的相平衡中既涉及化学平衡又涉及溶解平衡，其气液平衡数据不能用亨利定律简单描述，也很难用热力学理论准确推测，必须依靠实验。

本实验采用气相内循环动态法测定CO2—乙醇胺（MEA）水溶液系统的气液平衡数据，拟达到如下目的：(1)掌握气相内循环动态法快速测定气液相平衡数据的实验技术。

(2)学会通过相平衡数据的对比，优选吸收能力大，净化度高的化学吸收剂。

(3)加深对化学吸收相平衡理论的理解，学会用实验数据检验理论模型，建立有效的相平衡关联式。

B 实验原理气液相平衡数据的实验测定是化学吸收过程开发中必不可少的一项工作，也是评价和筛选化学吸收剂的重要依据。

气液平衡数据提供了两个重要的信息，一是气体的溶解度，二是气体平衡分压。

从工业应用的角度看，溶解度体现了溶液对气体的吸收能力，吸收能力越大，吸收操作所需的溶液循环量越小，能耗越低。

平衡分压反映了溶液对原料气的净化能力，平衡分压越低，对原料气的极限净化度越高。

因此，从热力学角度看，一个性能优良的吸收剂应具备两个特征，一是对气体的溶解度大，二是气体的平衡分压低。

由热力学理论可知，一个化学吸收过程达到相平衡就意味着系统中的化学反应和物理溶解均达到平衡状态。

若将平衡过程表示为：A（气）‖A（液）+ B（液）= M（液）定义：m 为液相反应物B的初始浓度（mol/l）；为平衡时溶液的饱和度，其定义式为：mB A M 的初始浓度液相反应物组分的浓度形式存在的以反应产物=θa 为平衡时组分A 的物理溶解量。

则平衡时，被吸收组分A 在液相中的总溶解量为物理溶解量a 与化学反应量θm 之和，由化学平衡和溶解平衡的关系联立求解，进而可求得气相平衡分压m p A和与θ*的关系： 在乙醇胺（MEA ）水溶液吸收CO 2系统中，主要存在如下过程：溶解过程： CO 2（g ）= CO 2（l ） （1）反应过程： 5.0<θ时， -++=+R N C O O R N H R N H l CO 222)( （2）5.0>θ时， -+-+=++322222H C O R N H O H CO RNCOO （3）本实验仅讨论5.0<θ时的情况。

气液相平衡实验数据处理气液相平衡实验是化学工程领域中的一项基础实验，主要用于研究和描述气体和液体之间相互作用的物理规律。

通过实验数据处理，我们可以得到气液相平衡实验的结果，并进行进一步的分析和解释。

一、实验原理气液相平衡实验是研究气体和液体之间相互作用的实验，主要涉及到气液相平衡的概念和原理。

在一定的温度和压力下，气体和液体之间会达到平衡状态，此时气体的溶解度与液体的蒸气压之间存在一定的关系。

通过对实验数据的处理和分析，我们可以得到气液相平衡的曲线和关系式，进而研究和描述气体和液体之间的相互作用。

二、实验步骤1.将实验装置加压至所需压力，保持稳定；2.记录实验过程中温度、压力和气体溶解度的变化；3.在实验结束后，将数据整理成表格；4.对数据进行处理和分析，得到气液相平衡曲线和关系式。

三、数据处理方法1.数据整理：将实验数据整理成表格，包括温度、压力、气体溶解度和时间等信息。

根据需要，可以对数据进行筛选和排序，以便更好地进行数据处理和分析。

2.数据拟合：采用最小二乘法等数学方法，将实验数据与气液相平衡关系式进行拟合。

通过拟合可以得到气液相平衡曲线和关系式，进而描述气体和液体之间的相互作用。

3.数据分析：对拟合得到的气液相平衡曲线和关系式进行分析，研究气体和液体之间的物理规律。

可以计算气体的溶解度和液体的蒸气压等物理量，进而得到气液相平衡的物理规律。

4.数据可视化：采用图表等方式将实验数据和处理结果进行可视化展示，以便更好地理解和解释气液相平衡实验的结果。

可以绘制气液相平衡曲线、溶解度曲线等图表，以便更好地研究和描述气体和液体之间的相互作用。

四、结论与展望通过气液相平衡实验数据的处理和分析，我们可以得到气体和液体之间的相互作用规律。

通过对数据的整理、拟合、分析和可视化展示，我们可以更好地理解和解释实验结果。

这些结果可以为化学工程领域中的其他研究提供重要的参考依据，也可以为工业生产中的气液相平衡问题提供理论支持和实践指导。

双液系的气液平衡相图实验报告一、实验目的1、测定常压下环己烷乙醇双液系的气液平衡相图。

2、掌握阿贝折射仪的使用方法。

二、实验原理两种液体物质混合而成的两组分体系称为双液系。

根据两组分间溶解度的不同，可分为完全互溶、部分互溶和完全不互溶三种情况。

本实验研究的是完全互溶双液系。

在一定温度下，溶液的气液两相达到平衡时，气相组成和液相组成之间存在一定的关系。

通过测定不同组成溶液的沸点和气、液相组成，绘制出沸点组成图（Tx 图），即可得到双液系的气液平衡相图。

通常，实验中通过测定溶液的折射率来确定其组成。

因为折射率与溶液的组成有一定的对应关系。

三、实验仪器和试剂1、仪器沸点仪阿贝折射仪超级恒温槽调压变压器温度计（50℃～100℃，分度值 01℃）移液管（1mL、2mL、5mL）洗耳球2、试剂环己烷（分析纯）无水乙醇（分析纯）四、实验步骤1、安装仪器将沸点仪洗净、烘干，安装好。

检查带有温度计的胶塞是否紧密，电热丝要靠近烧瓶底部的中心。

将阿贝折射仪与超级恒温槽连接好，调节恒温槽温度至 25℃。

2、配制溶液用移液管分别移取 05mL、10mL、15mL、20mL、25mL、30mL、35mL、40mL、45mL 乙醇于 10 个干燥的容量瓶中，再用环己烷分别稀释至刻度，摇匀，配制成一系列不同组成的环己烷乙醇溶液。

3、测定折射率用阿贝折射仪分别测定所配溶液及纯环己烷、纯乙醇的折射率。

测定时，用擦镜纸将棱镜擦净，滴加 2～3 滴待测液于棱镜上，合上棱镜并拧紧，调节反光镜使目镜内视场明亮，旋转棱镜调节旋钮，使目镜中出现明暗分界线，读取折射率。

每个样品测量三次，取平均值。

4、测定沸点向沸点仪中加入 20mL 乙醇含量较少的待测溶液，接通冷凝水。

调节调压变压器，缓慢加热溶液，当液体沸腾后，调节电压使液体沸腾稳定，待温度计读数稳定后，记录沸点温度。

停止加热，用吸管从小槽中吸取气相冷凝液，用阿贝折射仪测定其折射率。

再从侧管中吸取少量液相，测定其折射率。

课程名称：化工专业实验指导教师：李勇成绩：_________实验名称：气液平衡数据的测定同组学生姓名：一、实验目的和内容二、实验原理及数据处理依据三、实验装置与试剂四、操作方法和实验步骤五、数据记录及处理六、实验结论及误差分析七、分析和讨论汽液平衡数据是最常用的化工基础数据。

许多化工过程如精馏的设计、操作及过程控制等都离不开汽液平衡数据。

在热力学研究方面，新的热力学模型的开发，各种热力学模型的比较筛选等也离不开大量精确的汽液平衡实测数据。

现在，各类化工杂志每年都有大量的汽液平衡数据及汽液平衡测定研究的文章发表。

所以，汽液平衡数据的测定及研究深受化工界人士的重视。

一、实验目的和内容通过测定常压下乙醇—水二元系统汽液平衡数据的实验，使同学们了解、掌握汽液平衡数据测定的方法和技能，熟悉有关仪器的使用方法，将课本上学到的热力学理论知识与实际运用有机地联系在一起。

从而既加深对理论知识的理解和掌握，又提高了动手的能力。

气液平衡测定的种类：由于汽液平衡体系的复杂性及汽液平衡测定技术的不断发展，汽液平衡测定也形成了特点各异的不同种类。

按压力分，有常减压汽液平衡和高压汽液平衡。

高压汽液平衡测定的技术相对比较复杂，难度较大。

常减压汽液平衡测定则相对较易。

按形态分，有静态法和动态法。

静态法技术相对要简单一些，而动态法测定的技术要复杂一些但测定较快较准。

在动态法里又有单循环法和双循环法。

双循环法就是让汽相和液相都循环，而单循环只让其中一相（一般是汽相）循环。

在一般情况下，常减压汽液平衡都采用双循环，而在高压汽液平衡中，只让汽相强制循环。

循环的好处是易于平衡、易于取样分析。

根据对温度及压力的控制情况，有等温法与等压法之分。

一般，静态法采用等温测定，动态法的高压汽液平衡测定多采用等温法。

总之，汽液平衡系统特点各异，而测定的方法亦丰富多彩。

本实验采用的是常压下（等压）双循环法测定乙醇—水的汽液平衡数据。

二、实验原理及数据处理依据以循环法测定汽液平衡数据的平衡器类型很多，但基本原理一致，如图1所示，当体系达到平衡时，a、b容器中的组成不随时间而变化，这时从a和b两容器中取样分析，可得到一组汽液平衡实验数据。

双液系的气液平衡相图实验报告双液系的气液平衡相图实验报告一、引言在化学实验中，相图是研究物质在不同温度和压力下的相态变化规律的重要工具。

气液平衡相图是指在一定温度和压力下，气体和液体之间的平衡状态。

本实验旨在通过测定双液系的气液平衡相图，探究不同组分和温度对气液平衡的影响。

二、实验方法1. 实验仪器和试剂准备本实验所需的仪器有气相色谱仪、恒温水浴槽、压力计等。

试剂包括乙醇、水等。

2. 实验步骤(1) 准备双液系溶液：按照一定的比例将乙醇和水混合制备双液系溶液。

(2) 装填样品：将双液系溶液装填到气相色谱仪的样品瓶中。

(3) 设置温度：将恒温水浴槽的温度调至所需的实验温度。

(4) 测定平衡压力：将样品瓶放入恒温水浴槽中，等待一段时间使系统达到平衡，然后使用压力计测定平衡时的压力。

(5) 重复实验：重复以上步骤，测定不同组分和温度下的气液平衡压力。

三、实验结果根据实验数据，我们绘制了双液系的气液平衡相图。

图中横轴表示乙醇的摩尔分数，纵轴表示平衡时的压力。

我们可以观察到随着乙醇浓度的增加，平衡压力逐渐增大。

同时，随着温度的升高，平衡压力也呈现出上升的趋势。

这与理论预期相符。

四、讨论与分析通过实验结果，我们可以得出以下几点结论：1. 组分对气液平衡的影响：在双液系中，乙醇的浓度增加会导致平衡压力增加。

这是因为乙醇分子与水分子之间的相互作用力较强，使得乙醇分子更难从液相转移到气相，因而需要更高的压力才能达到平衡。

2. 温度对气液平衡的影响：随着温度的升高，气液平衡的压力也会增加。

这是由于温度升高会增加分子的热运动，使得气体分子更容易从液相转移到气相，因此需要更高的压力来保持平衡。

3. 实验误差分析：在实验过程中，由于仪器的精度限制和操作误差等因素的存在，实验结果可能存在一定的误差。

为了提高实验结果的准确性，我们可以增加重复实验次数，并进行数据的平均处理。

五、结论通过本实验，我们成功测定了双液系的气液平衡相图，并探究了组分和温度对气液平衡的影响。

实验数据处理（1） 乙醇浓度的计算利用实验参考书提供的乙醇标准曲线数据，由折光率和乙醇摩尔百分率关系用内插法得到乙醇摩尔分率如表1. 计算示例：以第一组气相为例第一组的气相折光率为1.3595落在折光率1.3594-1.3599之间，对应的乙醇摩尔分率为0.9379-0.8810.插值法计算如下： 1.3599−1.35950.8810−x =1.3599−1.35940.8810−0.9379解出x=0.9265,水的气相摩尔分率=1-x-=0.0735.（2） 温度计暴露温度校正n=t 观-（50-1.6*6.7），t 室=25℃，t 实际=t 观+0.00016n(t 观-t 室)；tp=t 实际+0.000125（t 室+273）（P-760），因为本小组实验的P 大于标准大气压，所以用P-760。

计算示例：以第一组为例；n=t 观-39.28=77.81-39.28=38.53，t 实际=77.81+0.00016*38.53*（77.81-25）=78.14℃ 平衡温度计算：tp=t 实际+0.000125（t 室+273）（P-760）=78.18+0.000125(25+273)(761.313-760)=78.19℃（3） 实验测得的温度和压强以及摩尔分率如表1、表二。

（4） 由所得的二元气液平衡数据表记录如表二。

活度计算示例：以第一组气相为例根据安托尼(Antoine)公式，lg(Ps)=A-B/(C + t/℃)，求出不同平衡温度下乙醇和水的饱和气压，乙醇的安托尼(Antoine)参数:A=8.21330,B=1652.050,C=231.480,水的安托尼(Antoine)参数：A=7.96681,B=1668.21,C=228。

计算乙醇的饱和蒸汽压：lgP=8.2133-1652.05/(231.48+78.19)，得P=755.879mmHg; 计算水的饱和蒸汽压：lgP=7.96681-1668.21/(228+78.19)，得P=330.029mmHg; 计算活度系数：由简化后的公式：0ip x py i ii =γ 乙醇的活度系数：γA=(P*yA)/(xA*P0)=(761.313*0.9265)/(0.8718*755.879)=1.0704 水的活度系数：γB=(P*yB)/(xB*P0)=(761.313*0.0735)/(0.1282*330.029)=1.3225（5） 由二元气液平衡数据绘制的相图如图2。

二元气液平衡数据测定实验报告实验目的：本实验旨在通过实验测定二元气液平衡数据，并分析其相关性，了解纯组分蒸汽与液相的平衡关系，为进一步研究混合气液平衡提供基础数据。

实验原理：二元气液平衡是指在一定温度下，两种组分的气相和液相之间达到平衡的状态。

根据国际公认的Raoult定律，对于理想混合物，每种组分在混合物中的蒸气压与该纯组分的蒸气压成正比。

即Pi = XiP0i，其中Pi为混合物中第i种组分的蒸气压，Xi为该组分的摩尔分数，P0i为该组分的纯物质蒸气压。

此外，根据Dalton定律，理想气体的总压等于各组分的部分压之和。

通过以上两个定律，可以得到二元气液平衡的相关参考内容。

实验装置：1. 气相分压计：采用测压瓶法，将采样气体与水或密度较小液体共同存在于测空间中，通过测压与摩尔分数可求得蒸汽压。

2. 饱和振荡测量器：通过振荡法测得溶液浓度与气相组成之间的关系。

3. 恒温浴：提供所需的恒定温度环境。

实验步骤：1. 将待测的液体样品加入恒温浴中进行稳定。

2. 将固定体积的气相样品加入气相分压计中，在恒定温度下测得其蒸汽压。

3. 将已测得的蒸汽压与相应的摩尔分数绘制成曲线图。

4. 使用饱和振荡测量器，在不同液相浓度下，测得溶液浓度与气相组成之间的关系。

5. 对数据进行处理，计算出相应的蒸汽压，绘制气液平衡曲线图。

实验结果及讨论：通过实验测得的数据，可以绘制出二元气液平衡曲线图。

从图中可以得到以下参数：1. 平衡液相摩尔分数：液相摩尔分数随气相摩尔分数的增加呈非线性变化，曲线上升趋势逐渐陡峭。

2. 气相浓度：随着液相摩尔分数的增加，气相浓度呈指数增加的趋势，达到一定浓度后趋于饱和。

3. 蒸汽压：蒸汽压与液相摩尔分数呈正相关关系，按照Raoult 定律计算得到的蒸汽压与实测值在误差范围内基本吻合。

根据实验数据，可以进一步分析二元气液平衡的相关性。

实验数据表明，气相组成受液相组成控制，随着液相摩尔分数的增加，气相组成趋向于饱和，即液相浓度越高，气相浓度也越高。

二元气液平衡数据测定实验报告实验报告：二元气液平衡数据测定一、实验目的：通过测定二元气液平衡数据，研究气体在液体中的分配行为，以建立气液平衡模型。

二、实验原理：气体在液体中的分配行为可由亨利定律描述，即气体在液体中的溶解度与气体分压成正比。

亨利定律的数学表达式可表示为：p = Kx其中，p为气体的分压（Pa），K为Henry常数，x为气体在液体中的溶解度（mol/L）。

三、实验仪器：1. 烧瓶：容积500 mL，带有橡胶塞和双口管。

2. 气密管：用于测定气体的分压。

3. 电子天平：用于称量实验用的液体和固体。

4. 温度计：用于测定溶液的温度。

四、实验步骤：1. 准备工作：将烧瓶与橡胶塞清洗干净，并在双口管中放入一根气密管。

2. 密封烧瓶：用一定量的溶剂（如水）填满烧瓶，将橡胶塞插入烧瓶口并封好。

3. 测定气体分压：将气密管插入烧瓶另一口，并用天平称量烧瓶与气密管的总重量。

然后通过称量所管道液体和固体的重量，并减去之前的总重量，即可得到气体的分压。

4. 测定溶解度：将气体分压值代入亨利定律的数学表达式，得到气体在溶液中的溶解度。

五、数据处理：根据实际测量得到的气体分压和溶解度数据，可绘制气体分压与溶解度之间的关系曲线。

在曲线上任取一点，可以计算该点的亨利常数。

六、实验结果与讨论：根据采集到的实验数据，绘制气体分压和溶解度之间的关系曲线，得到实验结果。

比较实验结果与理论值的差异，讨论可能的误差来源和实验条件的改进方法。

七、结论：通过本实验得到了二元气液平衡数据，研究了气体在液体中的分配行为。

实验结果表明，气体的溶解度与其分压成正比，符合亨利定律。

五、实验数据记录与处理：项目温度(0C)液相x 气相y饱和蒸汽压P s*100000数据1 正己烷74.468.8899 76.127 1.206289 正庚烷31.1101 23.873 0.472527数据2 正己烷76.472.2217 77.8291 1.280930 正庚烷27.7783 22.1709 0.505914数据3 正己烷79.156.6229 66.8828 1.383679 正庚烷43.3771 33.1172 0.553946数据4 正己烷82.550.4742 45.1909 1.530921 正庚烷49.5285854.8091 0.619527饱和蒸汽压的计算（c语言源程序）#include<stdio.h>#include<math.h>void main(){ int i;double pp[4],pg[4];double p=1.0158e5,t[4]={74.4,76.4,79.1,82.5};double A1=9.2164,B1=2697.55,C1=-48.78;//正己烷安托因方程系数double A2=9.2535,B2=2911.32,C2=-56.51;//正庚烷安托因方程系数for(i=0;i<4;i++){pp[i]=100000*exp(A1-B1/(t[i]+273.15+C1));// 正己烷饱和蒸汽压单位化为帕pg[i]=100000*exp(A2-B2/(t[i]+273.15+C2));//正庚烷饱和蒸汽压printf("pp[%d]=%lf\n",i,pp[i]);printf("pg[%d]=%lf\n",i,pg[i]);}}运行结果：Wilson方程计算（MACLAB源程序）function relixueclose all,clear,clc,t=[74.4,76.4,79.1,82.5]';x1=[0.688899,0.722217,0.566229,0.504742]';y1=[0.76127,0.778291,0.668828,0.451909]';x2=[0.311101,0.277783,0.433771,0.4952858]';y2=[0.23873,0.221709,0.331172,0.548091]';p=1.0258e5;ps1=[1.206289,1.280930,1.383679,1.530921]'*1.e5;ps2=[0.472527,0.505914,0.553946,0.619527]'*1.e5;V1=86/659;V2=100/684;x0=[10 10];x=lsqnonlin(@myfun,x0,[],[],optimset('Display','iter'),t,x1,y1,x2,y2,ps1,ps2,p,V1,V2); g12=x(1)g21=x(2)fprintf('EEA|NS2IEyIa:\n'),fprintf('g12=%f\tg21=%f\n',g12,g21),F=simulator(g12,g21,x1,x2,ps1,ps2,p,V1,V2,t);y1cal=F(:,1)y2cal=F(:,2)plot(x1,t,':>',y1cal,t,':d')legend('x1-t','y1-t')xlabel('x1,y1')ylabel('温度/t')title('正己烷T-x-y图')figureplot(x2,t,':>',y2cal,t,':d')legend('x2-t','y2-t')xlabel('x2,y2')ylabel('温度/t')title('正庚烷T-x-y图')figurex1=[1,0.688899,0.722217,0.566229,0.504742,0]';y1=[1,0.76127,0.778291,0.668828,0.451909,0]';y1cal=[ 1 y1cal' 0];plot(x1,y1,':>',x1,y1cal,':s')xlabel('x1')ylabel('y1')title('正己烷x-y图')legend('测量值','计算值')x2=[0,0.311101,0.277783,0.433771,0.4952858,1]';y2=[0,0.23873,0.221709,0.331172,0.548091,1]';y2cal=[ 0 y2cal' 1];figureplot(x2,y2,':>',x2,y2cal,':s')xlabel('x2')ylabel('y2')title('正庚烷x-y图')legend('测量值','计算值')function F=myfun(x,t,x1,y1,x2,y2,ps1,ps2,p,V1,V2)g12=x(1); g21=x(2);g21=x(2);A12=V2/V1*exp(-g12/8.314./(t+273.5));A21=V1/V2*exp(-g21/8.314./(t+273.15));gangma1=exp(-log(x1+A12.*x2)-x2.*(A12./(x1+A12.*x2)-A21./(x2+A21.*x1))); gangma2=exp(-log(x2+A21.*x1)-x1.*(A21./(x2+A21.*x1)-A12./(x1+A12.*x2))); y1cal=gangma1.*x1.*ps1/p;y2cal=gangma2.*x2.*ps2/p;F=[y1-y1cal;y2-y2cal];function F=simulator(g12,g21,x1,x2,ps1,ps2,p,V1,V2,t)A12=V2/V1*exp(-g12/8.314./(t+273.5))A21=V1/V2*exp(-g21/8.314./(t+273.15))gangma1=exp(-log(x1+A12.*x2)-x2.*(A12./(x1+A12.*x2)-A21./(x2+A21.*x1))) gangma2=exp(-log(x2+A21.*x1)-x1.*(A21./(x2+A21.*x1)-A12./(x1+A12.*x2))) y1cal=gangma1.*x1.*ps1/p;y2cal=gangma2.*x2.*ps2/p;F=[y1cal,y2cal]运行结果：Norm of First-orderIteration Func-count f(x) step optimality CG-iterations0 3 0.1122 6.37e-0051 6 0.110667 10 6.26e-005 12 9 0.107667 20 6.05e-005 13 12 0.101932 40 5.62e-005 14 15 0.0914919 80 4.79e-005 15 18 0.0745998 160 3.19e-005 16 21 0.055209 320 1.98e-005 17 24 0.0383033 640 7.13e-006 18 27 0.0351408 453.591 5.51e-007 1 Optimization terminated: first-order optimality less than OPTIONS.TolFun,and no negative/zero curvature detected in trust region model.g12 = -137.5221 g21 = 1.4686e+003EEA|NS2IEyIa:g12=-137.522127 g21=1468.583178A12 =1.17481.17451.17411.1736A21 =0.53700.53850.54060.5432gangma1 =0.85700.87450.79500.7649gangma2 =1.83781.87961.65811.5702F =0.6943 0.26340.7886 0.25750.6072 0.38840.5762 0.4697 y1cal =0.69430.78860.60720.5762y2cal =0.26340.25750.38840.4697。

双液系的气液平衡相图实验报告气液平衡相图是描述气体和液体在一定温度和压力下的平衡状态的图表，通过实验测定得到的数据可以绘制出相应的相图。

本实验旨在通过实验测定的数据，绘制出双液系的气液平衡相图，并对实验结果进行分析和讨论。

实验仪器和试剂。

实验中所使用的仪器包括压力计、温度计、烧瓶、试管等。

实验所需试剂为乙醇和水。

实验步骤。

1. 首先在烧瓶中加入一定量的水，并在试管中加入一定量的乙醇。

2. 将烧瓶和试管放入恒温水浴中，使其达到所需的温度。

3. 在一定时间间隔内，记录烧瓶内乙醇蒸气的压力和温度。

4. 根据实验数据，绘制出乙醇和水的气液平衡相图。

实验结果与分析。

通过实验测定得到的数据，我们成功绘制出了乙醇和水的气液平衡相图。

从实验结果可以看出，在一定温度下，乙醇和水的气液平衡曲线呈现出一定的规律性，随着温度的升高，气液平衡曲线也相应发生变化。

在实验过程中，我们还发现了一些异常现象，如在某些温度下，乙醇的蒸气压远大于预期值，经过分析发现可能是实验条件或者实验操作上的一些误差所致。

这些异常现象也为我们提供了更多的实验数据，有助于完善气液平衡相图的绘制。

结论。

通过本次实验，我们成功绘制出了乙醇和水的气液平衡相图，并对实验结果进行了分析和讨论。

实验结果表明，在一定温度和压力下，乙醇和水的气液平衡状态呈现出一定的规律性，同时也发现了一些异常现象，这为我们提供了更多的实验数据，有助于完善气液平衡相图的绘制。

总之，本次实验为我们提供了更深入的了解气液平衡相图的机会，并通过实验数据的分析，加深了我们对气液平衡相图的认识，为今后的研究和实验提供了重要的参考依据。

以上就是本次实验的实验报告，谢谢阅读。

二元气液平衡数据测定实验报告实验目的：本实验的目的是通过测定二元气液平衡数据，了解和研究物质在不同压力和温度下的相平衡情况，掌握相关的测量方法和数据处理技巧。

实验原理：二元气液平衡是指在一定温度和压力条件下，气体与液体之间达到平衡的状态。

在平衡状态下，气相和液相之间存在着平衡态的物质交换。

对于二元体系来说，平衡时液相的组成可以用熔点或沸点表示，而气相则可以用饱和蒸气压来表示。

因此，通过测量不同温度和压力下的饱和蒸气压和液相的组成，可以确定二元体系的气液平衡数据。

实验步骤：1.实验前准备：检查实验装置的密封性，准备好实验所需的试剂和设备。

2.组装实验装置：将液相样品装入恒温槽内，并连接好压力计、温度计、气体进口和出口管道。

3.调整温度：根据实验要求，调整恒温槽的温度至目标温度，并确保温度的稳定性。

4.调整压力：通过调整气体进口和出口的阀门，使压力计的指示保持在所需的压力范围内。

5.测量饱和蒸气压：根据实验要求，每隔一定温度间隔测定一次饱和蒸气压，并记录下相应的温度和压力值。

6.测量液相的组成：在平衡状态下，取一定量的液相样品，并进行化学分析或使用相应的设备测量其组成。

7.数据处理：根据测得的实验数据，绘制对应的平衡曲线或图表，并进行数据分析和讨论。

实验结果与讨论：根据所测得的二元气液平衡数据，可以得到平衡曲线和相应的饱和蒸气压与液相组成的关系。

通过分析实验结果，可以得到以下结论：1.在一定温度范围内，随着压力的升高，饱和蒸气压和液相组成均会增加。

2.对于不同的二元体系，其平衡曲线和相应的饱和蒸气压与液相组成的关系会有所不同，反映了体系的特性和组成。

3.可以根据平衡曲线和相应的饱和蒸气压与液相组成的关系，推导得到相应的热力学关系式，用于描述体系的相平衡情况。

实验结论：通过本次二元气液平衡数据测定实验，我们了解到了不同温度和压力下的气液平衡情况，并掌握了相关的实验技巧和数据处理方法。

实验结果显示，二元体系的饱和蒸气压和液相组成与温度和压力有密切关系，对于不同的体系会有所差异。

甲醇异丙醇二元气液相平衡数据的测定甲醇和异丙醇是两种常见的有机化合物，在化工生产和实验室中都有广泛的应用。

研究它们之间的气液相平衡数据对于深入理解它们的性质和相互作用至关重要。

本文将讨论如何进行甲醇和异丙醇的二元气液相平衡数据的测定，并探讨实验结果的意义和应用。

为了测定甲醇和异丙醇的二元气液相平衡数据，我们需要进行一系列的实验。

通常情况下，可以采用等温法或者升温法来进行实验。

在等温法实验中，首先需要准备一定量的甲醇和异丙醇混合物，并将其置于恒温恒压的条件下。

然后通过逐渐升高温度，观察并记录不同温度下的液相和气相组成，从而得到气液相平衡数据。

在实验过程中，需要注意控制好温度和压力的稳定性，以确保实验结果的准确性和可靠性。

此外，还需要注意实验装置的密封性和操作规范，以避免实验中出现外界干扰因素导致数据失真。

通过实验测定得到的甲醇和异丙醇的二元气液相平衡数据可以用于研究它们之间的相互作用和溶解度规律。

这些数据对于优化化工生产过程、设计分离工艺以及开发新的材料具有重要的指导意义。

例如，可以利用这些数据来确定甲醇和异丙醇在不同温度和压力下的最佳混合比例，从而提高生产效率和产品质量。

甲醇和异丙醇的二元气液相平衡数据还可以用于计算它们之间的相互溶解度和热力学性质。

通过分析这些数据，可以进一步揭示它们之间的相互作用机制和分子结构，为深入理解有机化合物之间的相互作用提供重要参考。

总的来说，通过测定甲醇和异丙醇的二元气液相平衡数据，可以深入了解它们之间的相互作用和性质，为有机化合物的研究和应用提供重要参考。

这些数据不仅对于优化生产工艺、设计新材料具有重要意义，同时也为理论研究和实验研究提供了有力支持。

希望本文的内容能够对相关领域的研究工作有所启发，促进有机化学领域的发展和进步。