《刚体力学作业》

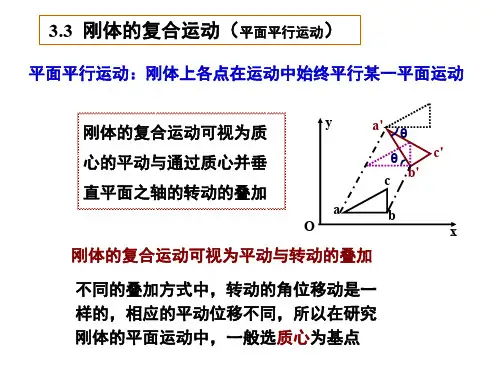
物理学（作业题参考解答）第一章 质点运动学作业题：1-3； 1-5；1-8；1-11； 1-16作业题解答（参考）1-3 解：（1）t x 2=，22t y -=，422x y -=（x ＞0）（2）()()j i r 222t t -+=； 1=t s 到2=t s ，()()j i r 2r r v 32121-=--==t ∆∆（m·s -1） （3）()j i rv t t22d d -==； 1s 末和2s 末， ()j i v 221-=（m·s -1）， ()j i v 422-=（m·s -1） （4）j va 2dtd -==，()()j a a 221-==（m·s -2） 1-5 解：t d d r v =，t d d v r =()()()()()()t0000v t 0t dt v t t dt t t v t 1t cos sin sin cos sin cos ωωωωωωωω-==+=-=+-⎡⎤⎣⎦⎰⎰t tr r v i j i j i j()j i r ⎪⎭⎫⎝⎛+-+=R t v v t v t ωωωωωcos sin 000， t v x ωωsin 0=，t v R v y ωωωcos 00-+= 将上两式中消去t 得质点的轨迹方程为 20202⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛--+ωωv v R y x1-8 解：3kv a -= ( k > 0，常数)， 3d d kv t v -=或t k v v d d 3-=；⎰⎰-=tv v t k v v3d d 0 21200211)(⎪⎪⎭⎫⎝⎛+=t kv v t v ，t t kv v x d 211d 21200⎪⎪⎭⎫ ⎝⎛+=;t t kv v x x d 211d 21200t0⎪⎪⎭⎫ ⎝⎛+=⎰⎰，()1211)(20-+=t kv kv t x ， xvv t x x v t v d d d d d d d d =⋅=，3kv a -=，x k vvd d 2-=， x kv v x v 001)(+= 1-11 解：t t t612d d 2-==ωβ；()t t t d 612d 2-=ω； ()⎰⎰-=t t t t2d 612d ωω2334t t -=ω（1s rad -⋅）；t t R a t 6122-==β（2s m -⋅）1-16：解：B A A v v v 地对对地对＋＝B ；由于对地地对－B Bv v =对地对地对－＝B B v v v A A ；A 机相对于B 机的速度大小为αcos 222B A B A AB v v v v v -+= )s m (91760cos 8001000280010001o 22-⋅=⨯⨯⨯-+=6540917866.0800arccos 30cos arccos o o '=⨯==AB B v v β第二章 质点动力学作业题：2-3；2-4；2-6；2-9；2-11；2-12；2-14；2-15；2-20作业题解答（参考）2-3 解：⎪⎪⎭⎫ ⎝⎛=-lv m mg T 2cos θ；⎪⎭⎫ ⎝⎛=-t v m mg d d sin θ；θθθd d d d sin ⎪⎭⎫ ⎝⎛=-t v m mg ()ωθθθl t m mg d d d d sin ⋅⎪⎭⎫⎝⎛=-； ωωθθd d sin ⋅-=l g⎰⎰⋅-=ωωθωωθθ0d d sin 0l g ；解得()2202121cos 1ωωθl l g -=- ()()1cos 211cos 22020-+=-+=θθωωgl v l g l ；⎪⎪⎭⎫ ⎝⎛+-=θcos 3220g g l v m T2-4 解：根据牛顿定律有 t v mt d d 40120=+；即0.40.12d d +=t tv； ()⎰⎰+=tvv t t v 0d 0.40.12d 0； )0.60.40.6(2t t v ++=m·s -1即20.60.40.6d d t t tx ++=；()t t t x x x t d 6.04.06.0d 002⎰⎰++=；)m 02020605(32t .t .t ..x +++=2-6 解：tv m kmv mg d d 2=--；y v v t yy v t v d d d d d d d d =⋅=，积分⎰⎰+-=y v v kv g v v y 020d d ⎪⎪⎭⎫ ⎝⎛++-=202ln 21kv g kv g k y ；最高处时，v =0，⎪⎪⎭⎫ ⎝⎛+==g kv g k y h 20max ln 21 (1) tv mkmv mg d d 2=+-；y v v t yy v t v d d d d d d d d =⋅=，y v mv kmv mg d d 2=+- ⎰⎰--=02d d hvkv g vv y ； 解出 12001-⎪⎪⎭⎫ ⎝⎛+=g kv v v2-9 解法1：根据动量原理得x x mv I -=0；0-=y y mv IgH v y 2=；gH v m I I I x y x 2222+=+=32.7108.922030.02=⨯⨯+⨯=)s N (⋅70020108922tan ..v gH mv mv I I x xy xy -=⨯⨯-=-=-==α， ︒=145α 小球所受到的平均冲力大小为)N (36602.032.7===t I F 2-11 解：()()u v m Mv v m M -+=+αcos 0可得人的水平速率的增量为u mM mv v v +=-=α∆cos 0g v t αsin 0=；所以人跳跃抛出物体后增加的距离为()u gm M mv t v x +=⋅=αsin ΔΔ0 2-12 解：0321=++p p p ；213p 10-==201007.1-⨯=（1s m kg -⋅⋅）3p 与1p 的夹角为8514933.522.9arctan 90arctan9021'︒=+︒=+︒=p p α2-14 解：yg mg F λ-=；()y g y m y F W d d d λ-==把水桶从水面提高到井口外力所做的总功 ()(J)882d 10=-=⎰y g y m W λ2-15 解： x x m F a 4.03.01043+=+==（m·s -2）； 以3=x m 代入上式得5.1=a m·s -2 ；()⎰⎰+==-3030202d 43d 2121x x x F mv mv ()2723302=+=x x ；3.210272=⨯=v （m·s -1）2-20 解：第一个过程：210122121v m kx = 第二个过程：020=v ，则2m 碰后的速度为 102v v =第三个过程：()22222221cos 21v m R R g m v m ++=α根据牛顿定律得 Rv m N g m 222cos =+α可解得 kmgRk gR m x 27271==第三章 刚体力学作业题：3-1；3-5；3-8；3-11；3-12；3-15；3-16；3-18；3-20作业题解答（参考）3-1 解：(1)()()()2-33120s rad 1136012102110721432602⋅=⨯⨯-⨯⨯⨯=-=-=....t n n tπωωβ(2) ()()12212120606022160221n n tt t n n t n t t ＋πππβωθ=-⋅+=+= ()()()圈390602102172126022312=⨯⨯+⨯=⨯+==..n n t N πθ3-5 解： 1.0)300500(2⨯+==t .t .Fr M根据转动定律tJ J M d d ωβ==， 得t t t t J M d 101.00.300.50d d 3-2⨯+==ω ()3202100250d 300500d t t t t t +=+==⎰⎰ωωωω；t =3s ，()-1332s rad 1095431003250⋅⨯=⨯+⨯=.ω3-8 解：θλθcos d cos d d gr r r g m M ⋅=⋅⋅=；br a +=λ()θθcos 32d cos 2gl bl a r gr br a M l⎪⎭⎫ ⎝⎛+=+=⎰ ()()43022024131d d d bl al r br a r r r m r J ll 0l +=+===⎰⎰⎰λθωωθθωωd d d d d d d d J t J t JM =⋅==，θωωθd d 4131cos 32432⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+bl al gl bl a ωωθθωπd 4131d cos 3204322⎰⎰⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+bl al gl bl a ； ()()bl a l bl a g 34234++=ω3-11 解： ()J 109716030210004212142321k 1⨯=⎪⎭⎫ ⎝⎛⨯⨯⨯⨯==..J E πω()J 101926010210004212132322k 2⨯=⎪⎭⎫ ⎝⎛⨯⨯⨯⨯==..J E πω()J 10751109711012443k 1k 2⨯-=⨯-⨯=-=...E E W3-12 解：（1）)2Rm πσ=，r r RmS m d 2d d 2ππσ== 2r/R gmr 2m g F d d d μμ==；mgR r/R gmr M Rμμ⎰-=-=02232d 2RgJ M 34μβ-==；t βωω=-0，g R t μωβωω4300=-= （2）根据动能定理，摩擦力的功为 2022041210ωωmR J W -=-=3-15 解：(1)⎰∆===∆t Fl t M J L d 0ω（2）()θωcos 1212120-=mgl J ；解得 ⎪⎪⎭⎫ ⎝⎛∆=gl m t F 2223-1arccos θ3-16 解：kt m = 其中，-13s kg 10⋅=-k 。

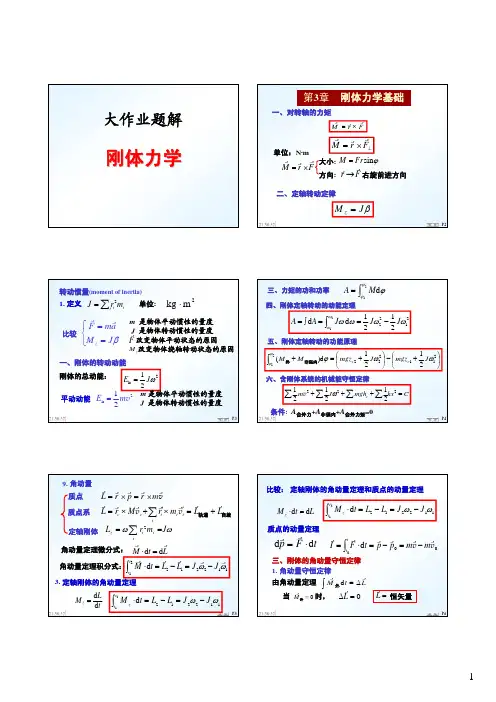
作业1 质点运动学(一)参考答案1. B ；2. D;3. 8m, 10m.4. 3, 3 6;5. 解：(1) 5.0/-==∆∆t x v m/s(2) v = d x /d t = 9t - 6t 2v (2) =-6 m/s(3) S = |x (1.5)-x (1)| + |x (2)-x (1.5)| = 2.25 m6. 答：矢径r是从坐标原点至质点所在位置的有向线段．而位移矢量是从某一个初始时刻质点所在位置到后一个时刻质点所在位置的有向线段．它们的一般关系为0r r r-=∆0r 为初始时刻的矢径, r 为末时刻的矢径，△r为位移矢量．若把坐标原点选在质点的初始位置，则0r =0,任意时刻质点对于此位置的位移为△r =r，即r既是矢径也是位移矢量．1. D ；2. -g /2 ， ()g 3/322v3. 4t 3-3t 2 (rad/s)， 12t 2-6t (m/s 2)4. 17.3 m/s, 20 m/s .5. 解： =a d v /d t 4=t ， d v 4=t d t⎰⎰=vv 0d 4d tt tv 2=t 2v d =x /d t 2=t 2t t x txx d 2d 020⎰⎰=x 2= t 3 /3+x 0 (SI)6. 解：根据已知条件确定常量k()222/rad 4//s Rt t k ===v ω24t =ω, 24Rt R ==ωvt=1s 时， v = 4Rt 2 = 8 m/s2s /168/m Rt dt d a t ===v 22s /32/m R a n ==v()8.352/122=+=nt a a a m/s 21.D2.C3.4. l/cos 2θ5.如图所示，A ，B ，C 三物体，质量分别为M=0.8kg, m= m 0=0.1kg ，当他们如图a 放置时，物体正好做匀速运动。

（1）求物体A 与水平桌面的摩擦系数；（2）若按图b 放置时，求系统的加速度及绳的张力。

1刚体系统静力学作业一、是非题判断任意两个力都可以简化为一个合力。

力偶可以从刚体的作用平面移到另一平行平面，而不改变它对刚体的作用效应。

平面一般力系的合力对作用面内任一点的矩，等于力系各力对同一点的矩的代数和。

如果作用在刚体上的力系的主矢等于零，即力多边形自行封闭，则此力系平衡。

作用与反作用力是一对等值、反向、共线的平衡力。

力对一点的力矩矢在通过该点的任一轴上的投影等于这个力对该轴的力矩。

若作用在刚体上的三个力的作用线汇交于同一个点，则该刚体必处于平衡状态。

力是滑移矢量，力沿其作用线滑移不改变对物体的作用效果。

力沿坐标轴分解就是力向坐标轴投影。

力偶系的主矢为零。

若一平面力系对某点之主矩为零，且主矢亦为零，则该力系为一平衡力系。

力系向一点简化的理论依据是力的平移定理。

平行力系中心只与力系各力的大小和作用点有关，而与各力的方向无关。

二、填空题1、平面汇交力系平衡的几何条件是( )。

2、力偶的三要素是( )、( )和( )。

3、平面力系二矩式平衡方程的附加条件是( )。

4、静力学四大公理中只适用于刚体的公理是( )。

5、作用在刚体上的两个力偶的等效条件是( )。

6、作用在刚体上的三个力使刚体处于平衡状态，则这三个力必然( )。

三、已知：q=20KN/m, P=100KN, m=50KN.m ,图中1、2、3杆及杆ＡＢ的自重均不计，求1、2、3杆受力。

四、铰链支架有两杆AD、CE和滑轮组成，B处为铰链，尺寸如图示。

滑轮上吊有Q=10KN 的重物，求固定铰链支座A和E的约束反力。

已知R＝0.50m，r=0.25m。

五、求图示梁A、B处反力。

第三章 刚体力学基础 课后作业班级 姓名 学号一、选择题1、一个质点作简谐振动，振幅为A ，在起始时刻质点的位移为2A , 且向x 轴正方向移动，代表此简谐振动的旋转矢量为( )1、有两个力作用在一个有固定转轴的刚体上：(1) 这两个力都平行于轴作用时，它们对轴的合力矩一定是零；(2) 这两个力都垂直于轴作用时，它们对轴的合力矩可能是零；(3) 当这两个力的合力为零时，它们对轴的合力矩也一定是零；(4) 当这两个力对轴的合力矩为零时，它们的合力也一定是零．对上述说法下述判断正确的是( )(A ) 只有(1)是正确的 (B )(1)、(2)正确，(3)、(4)错误(C ) (1)、(2)、(3)都正确，(4)错误 (D )(1)、(2)、(3)、(4)都正确2、关于力矩有以下几种说法：(1) 对某个定轴转动刚体而言，内力矩不会改变刚体的角加速度；(2) 一对作用力和反作用力对同一轴的力矩之和必为零；(3) 质量相等，形状和大小不同的两个刚体，在相同力矩的作用下，它们的运动状态一定相同．对上述说法下述判断正确的是( )(A ) 只有(2)是正确的 (B ) (1)、(2)是正确的(C )(2)、(3)是正确的 (D ) (1)、(2)、(3)都是正确的3、均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴转动，如图所示，今使棒从水平位置由静止开始自由下落，在棒摆到竖直位置的过程中，下述说法正确的是( )(A ) 角速度从小到大，角加速度不变(B ) 角速度从小到大，角加速度从小到大(C ) 角速度从小到大，角加速度从大到小(D ) 角速度不变，角加速度为零4、 一圆盘绕通过盘心且垂直于盘面的水平轴转动，轴间摩擦不计．如图射来两个质量相同，速度大小相同，方向相反并在一条直线上的子弹，它们同时射入圆盘并且留在盘内，则子弹射入后的瞬间，圆盘和子弹系统的角动量L以及圆盘的角速度ω的变化情况为( ) (A) L 不变，ω增大 (B) 两者均不变(C) L不变，ω减小 (D) 两者均不确定5、假设卫星环绕地球中心作椭圆运动，则在运动过程中，卫星对地球中心的( )(A) 角动量守恒，动能守恒 (B) 角动量守恒，机械能守恒(C) 角动量不守恒，机械能守恒 (D) 角动量不守恒，动量也不守恒(Ｅ) 角动量守恒，动量也守恒二、填空题1、有甲、乙两个飞轮，甲是木制的，周围镶上铁制的轮缘。

理论力学8章作业题解8-2 半径为r 的齿轮由曲柄OA 带动，沿半径为R 的固定齿轮滚动。

如曲柄OA 以匀角加速度a 绕O 轴转动，且当运动开始时，角速度00=w ，转角0=j 。

求动齿轮以中心Ａ为基点的平面运动方程。

解：图示，A 轮平面运动的转角为=A j ∠C 3AC 2=j +∠CAC 2由于弧长CC 1=CC 2，故有 ∠CAC 2=r R /j ，所以22/t rr R r r R r R A a j j j j +=+=+=A 轮平面运动方程为ïïîïïíì+=+=+=+=+=22212212)sin()()sin()()cos()(cos )(tr r R t r R r R y t r R r R x A A A a j a j a j8-6两刚体M ，N 用铰C 连结，作平面平行运动。

已知AC=BC=600mm ，在题附图所示位置s mm v s mm v B A /100,/200==，方向如图所示。

试求C 点的速度。

解：由速度投影定理得()()0==BC C BC B v v 。

则v C 必垂直于BC 连线，v C 与AC 连线的夹角为30°。

由()()AC A AC C v v = 即得：s mm v v A C /200== ，方向如题4-6附图示。

解毕。

8-9 图所示为一曲柄机构，曲柄OA 可绕O 轴转动，带动杆AC 在套管B 内滑动，套管B 及与其刚连的BD 杆又可绕通过B 铰而与图示平面垂直的水平轴运动。

已知：OA ＝BD ＝300mm ，OB ＝400mm ，当OA 转至铅直位置时，其角速度ωo ＝2rad/s ，试求D 点的速度。

C 12Aj C解 (1)平面运动方法： 由题可知：BD AC w w =确定AC 杆平面运动的速度瞬心。

套筒中AC 杆上一点速度沿套筒(为什么？)s rad IAOA IA v A AC /72.00=´==w w , s mm BD BD v AC BD D /216=´=´=w w D 点加速度如何分析？关键求AC 杆角加速度(=BD 杆角速度) 基点法，分析AC 杆上在套筒内的点(B’)：(1) tA B n A B A B a a a a ¢¢¢++=r r r r大小：× ∠ ∠ × 方位：× ∠ ∠ ∠ 再利用合成运动方法：动点：套筒内AC 杆上的点B’，动系：套筒。