数控车床加工椭圆的方法
- 格式:doc
- 大小:27.50 KB
- 文档页数:5

数控车床加工椭圆类零件的初步探讨Establish noble character. On the morning of October 2, 2022数控车床加工椭圆类零件的初步探讨摘要:本文以SIEMENS802S/C 数控系统为例,介绍在数控车床上加工椭圆类零件的多种方法;采用圆弧逼近法—四心法,可以采用一般G指令加工出精度要求不高的椭圆形状;采用直线逼近法—参数编程,可以加工出精度要求高的椭圆形状;关键词:数控车床车削椭圆类零件圆弧逼近法直线逼近法 R参数在技工学校高级数控的培训课题中,椭圆类零件的加工是不可或缺的内容;椭圆的加工属于非圆曲线的特殊零件加工,相对比较复杂;在数控车床上加工该类零件,我们一般采用逼近法:圆弧逼近法和直线逼近法;1、圆弧逼近法圆弧逼近法是采用多段圆弧逼近椭圆的加工方法,利用机械制图中绘制椭圆的近似画法四心法,求得多段圆弧的切点和半径来加工椭圆;在加工精度要求比较低的情况下可以考虑用此方法;1加工原理通过机械制图近似绘制椭圆的方法,画出椭圆;椭圆是由四段圆弧组成的;如图1所示;①画出长轴AB与短轴CD,连接AC并在AC上截取AF,使其等于AO与CO之差CE.②作AF的垂直平分线,使其分别交于AB和CD于O1点和O2点;③分别以O1点和O2点为圆心,O1A和O2C为半径作出圆弧AG和CG,,该圆弧即为四分之一的椭圆;④用同样的方法画出整个椭圆;2计算组成椭圆的四段圆弧半径、切点坐标等数据;3编写加工程序只要计算出如O1、O2、G点坐标,O1A和O2C的半径数值等就很容易编写加工这四段圆弧的程序;2、直线逼近法直线逼近法是采用多段直线逼近椭圆的加工方法,应用这种方法加工非圆曲线时,只要步距足够小,在工件上所形成的最大误差,就会小于所要求的最小误差,从而加工出标准的椭圆;常用的直线逼近法,加工精度高;直线逼近法加工椭圆是通过参数编程来加工的,用数控车床的普通G代码指令是难以加工的;参数编程指令适合抛物线、椭圆、双曲线等非圆曲线编程,还适合于图形相同,只是尺寸不同的系列零件编程,同样适用于工艺路径一样,只是位置数据不同的系列零件的编程;使用参数编程可以极大的提高编程效率,大大简化程序,并能够扩展数控机床的使用范围;本文主要以SIEMENS802S/C 数控系统为例,介绍使用参数编程加工椭圆的方法;1 加工原理 SIEMENS系统中R参数作为变量,通过对R参数进行赋值、运算等处理,从而使程序实现规律变化的动作,从而提高编程的灵活性和适用性;使用R参数编程时可以用变量代替具体数值,因而在加工同一类的零件时,只需要将实际的值赋予变量即可,不需要对每一个零件都编一个程序;2程序的编写方法在编写时需根据零件加工的图纸已知条件,选择椭圆方程的极坐标方式还是直角坐标方式,从而确定参数编程的具体编写方法;3椭圆的极坐标方程为x=bxsinβ; z=axcosβ椭圆的直角坐标方程为:x2 /b2 +z2 /a2 =13、实例加工加工如图2零件,材料为45号钢,毛坯32 x100,T1尖刀;1四心法加工椭圆如果零件对椭圆精度要求不高,则采用四心法来加工;①用计算机绘制测绘的方法绘制椭圆;②测量出四段圆弧的半径、切点;如图3所示;SIEMENS802S/C 精加工参考程序毛坯:32 x100G90 G95 G54 M08M03S1600T1尖刀G00 X35 Z5G01 X0 0 FG03 CR=CR=G01 Z-60X 33G00 X100 Z100M09M302参数编程加工椭圆如果零件对椭圆精度要求高,则须采用参数编程来加工 ;①直角坐标方程编程如果已知椭圆终点坐标X值或Z值;根据椭圆方程分析加工零件的已知条件;由椭圆直角坐标方程公式x2 /b2 +z2 /a2 =1知:长轴a=20 短轴b=13,椭圆终点坐标z= 终点坐标x可以不知道 SIEMENS802S/C 精加工参考程序毛坯:32 x100G90 G95 G54 M08M03 S1600T1尖刀G00 X35 Z5G01X0 0 FR1=13MA1:R2=13/20SQRT2020-R1R1G01 X=2R2 Z=R1-13R1=IF R1>= GOTOB MA1G01X35G00X100 Z100M09M30②极坐标方程编程如果已知椭圆终点坐标的转角a或极坐标β;例:加工图4所示椭圆零件,已知椭圆终点转角,此时,需要利用极坐标方程来加工椭圆;已知椭圆终点转角α如何求得椭圆终点极坐标角度β;由极坐标法绘制椭圆的公式x=bxsinβ; z=axcosβ,终点转角a=1300,长轴a=20,短轴b=13,如图5所示,须求得椭圆终点极坐标角度 ;通过如图6所示的几何角度分析,求得a和β值之间的关系式:已知a,求β设长轴a=20=OC,短轴b=R13=OD解:∵tan a=AB/OAAB=AC-BC=a x sinβ–a-b x sinβ= b x sinβOA=a x cosβtan a=AB/OA=b/a tanβ∴tanβ=a/b tan a∴β=cota/b tan a结果求得:β=cot20/13 tan130=cot==SIEMENS802S/C 精加工参考程序毛坯:32 x100G90 G95 G54 M08M03 S1600T1尖刀G00 X35 Z5G01X0 0 FR1=20 R2=13 R3=0 R4=MA2: R5=R1COSR3 R6=R2SINR3G01 X=2R6 Z=R5-13R3=R3+IF R3<=R4 GOTOB MA2G01 X35G00X100 Z100M09M304、技术探讨在SIEMENS802S/C系统上进行椭圆类零件的粗、精加工,怎样编程下面介绍一种编程方法,可以解决该类零件的粗、精加工的问题;见图4椭圆部分例:G90 G95 G54 G00X35 Z5M03 S500 G01X0 0 FT1尖刀粗加工 R2=13G00 X35 Z5 MA2: R3=13/20SQRT2020-R2R2R1=5 G01 X=2R3 Z=R2-13G158 X=R1 Z=0 R2=MA1: AA1 IF R2>= GOTOB MA2R1=R1-1 G01X35IF R1>=0 GOTOB MA1 G00Z5G01X35 M17G00Z5S1600精加工G01X0 0 FAA1G01X35G00X100 Z100M305、加工效果用参数编程编制此类特殊零件的加工程序的基本思路就是用小直线段来逼近椭圆;只要控制好小直线段的距离,保证线轮廓度达到图纸要求,就可以达到加工要求了;。

数控车床加工椭圆的宏程序随着数控技术不断进步, 数控车床加工中各种复杂形面也日渐增多, 如椭圆、抛物线、正弦曲线、余弦曲线、双曲线等各种非圆曲面。
对于上述各种复杂成形面, 利用CAM 软件进行自动编程相对简单, 但由于种种原因, 在绝大多数情况下数控车床主要还是依靠手工编程。
椭圆轴线与数控车床Z 轴重合的情形相对比较简单, 其解决方案也多见于各类文献, 但在本例中椭圆轴线与数控车床Z 轴呈一定夹角, 编程和加工难度陡增,主要原因如下: ①机床数控系统本身既不存在加工椭圆等非圆曲线的G 指令, 更没有类似G68 这样的旋转指令, 使编程难度大大增加。
②加工中变量的参数直接影响着加工的效率以及质量, 很容易产生过切报警, 即使程序正确无误, 实际加工时的参数调整也非常困难, 直接影响着加工能否顺利进行, 以及加工精度能否保证。
总而言之, 目前尚未见有表述类似实例的文章。
本实例进行了有益的尝试和探索, 给出了切实可行的解决方案, 为类似问题提供了难得的参考及借鉴。
椭圆宏程序的编制如下。
1. 椭圆方程宏程序主要利用各种数学公式进行运算加工, 因此编制旋转椭圆程序操作者必须要掌握椭圆方程和旋转公式等各种数学公式的计算方法并加以灵活运用。
椭圆方程有两种形式, 分别是椭圆的标准方程和参数方程。
椭圆标准方程:椭圆参数方程:其中a 、b 分别为X、Z 所对应的椭圆半轴。
2. 旋转公式由于数控车床并不像加工中心那样存在着旋转指令, 所以要利用旋转公式来进行椭圆的旋转。
旋转公式的定义:如图1 所示, 平面上绕点O 旋转, 使平面上任意一对对应点P 和P′与一个定点O 连接的线段都相等, 即OP = OP′, 且角∠POP′等于角θ, 点O称为旋转中心, 角θ称为旋转角。
旋转公式: 如图1 所示, 取直角坐标系, 以原点O为旋转中心, 旋转角为θ, 平面上任意一点P ( x, z) 旋转到P′( x′, z′) , 令∠XOP= α, 则∠XOP′= α+ θ, 且OP = OP ′。

数控车床加工对象为各种类型的回转面,其中对于圆柱面、锥面、圆弧面、球面等的加工,可以利用直线插补和圆弧插补指令完成,而对于椭圆等一些非圆曲线构成的回转体,加工起来具有一定的难度。
这是因为大多数的数控系统只提供直线插补和圆弧插补两种插补功能,更高档的数控系统提供双曲线、正弦曲线和样条曲线插补功能,但是一般都没有椭圆插补功能。
因此,在数控机床上对椭圆的加工大多采用小段直线或者小段圆弧逼近的方法来编制椭圆加工程序。
在这里结合工作实践对车削椭圆轮廓的宏程序的编制方法进行探讨。
一、椭圆宏程序的编制原理数控系统的控制软件,一般由初始化模块、输入数据处理模块、插补运算处理模块、速度控制模块、系统管理模块和诊断模块组成。
其中插补运算处理模块的作用是依据程序中给定的轮廓的起点、终点等数值对起点终点之间的坐标点进行数据密化,然后由控制软件,依据数据密化得到的坐标点值驱动刀具依次逼近理想轨迹线的方式来移动,从而完成整个零件的加工。
依据数据密化的原理,我们可以根据曲线方程,利用数控系统具备的宏程序功能,密集的算出曲线上的坐标点值,然后驱动刀具沿着这些坐标点一步步移动就能加工出具有椭圆、抛物线等非圆曲线轮廓的工件。
二、椭圆宏程序的编制步骤宏编程一般步骤:1.首先要有标准方程(或参数方程)一般图中会给出。
2.对标准方程进行转化,将数学坐标转化成工件坐标标准方程中的坐标是数学坐标,要应用到数控车床上,必须要转化到工件坐标系中。
3.求值公式推导利用转化后的公式推导出坐标计算公式4.求值公式选择根据实际选择计算公式5.编程公式选择好后就可以开始编程了三、加工实例下面分别就工件坐标原点与椭圆中心重合,偏离等2种情况进行编程说明。
(1)工件坐标原点与椭圆中心重合椭圆标准方程为①转化到工件坐标系中为②根据以上公式我们可以推导出以下计算公式③④在这里我们取公式③。
凸椭圆取+号,凹椭圆取-号。
即X值根据Z值的变化而变化,公式④不能加工过象限椭圆,所以舍弃。
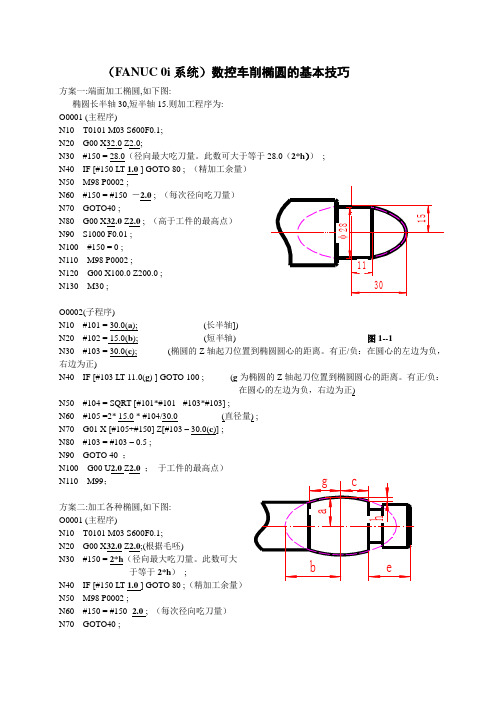
(FANUC 0i 系统)数控车削椭圆的基本技巧方案一:端面加工椭圆,如下图:椭圆长半轴30,短半轴15.则加工程序为: O0001 (主程序)N10 T0101 M03 S600F0.1; N20 G00 X32.0 Z2.0;N30 #150 = 28.0(径向最大吃刀量。
此数可大于等于28.0(2*h )) ; N40 IF [#150 LT 1.0 ] GOTO 80 ; (精加工余量) N50 M98 P0002 ;N60 #150 = #150 -2.0 ; (每次径向吃刀量) N70 GOTO40 ;N80 G00 X 32.0 Z 2.0 ; (高于工件的最高点) N90 S1000 F0.01 ; N100 #150 = 0 ; N110 M98 P0002 ;N120 G00 X100.0 Z200.0 ;N130 M30 ;O0002(子程序)N10 #101 = 30.0(a ); (长半轴])N20 #102 = 15.0(b ); (短半轴) 图1--1N30 #103 = 30.0(c ); (椭圆的Z 轴起刀位置到椭圆圆心的距离。
有正/负:在圆心的左边为负,右边为正)N40 IF [#103 LT 11.0(g ) ] GOTO 100 ; (g 为椭圆的Z 轴起刀位置到椭圆圆心的距离。
有正/负:在圆心的左边为负,右边为正)N50 #104 = SQRT [#101*#101 - #103*#103] ;N60 #105 =2* 15.0 * #104/30.0 (直径量) ; N70 G01 X [#105+#150] Z[#103 – 30.0(c )] ; N80 #103 = #103 – 0.5 ; N90 GOTO 40 ;N100 G00 U 2.0 Z 2.0 ; 于工件的最高点) N110 M99;方案二:加工各种椭圆,如下图: O0001 (主程序)N10 T0101 M03 S600F0.1;N20 G00 X 32.0 Z 2.0;(根据毛呸)N30 #150 = 2*h (径向最大吃刀量。

CAD/CAM与制造业信息化60椭圆的数学模型建立及数控车削手工编程撰文/江苏省盐城市教育科学研究院 解太林椭圆属于非圆曲线,在数控车床加工中,非圆曲线工件的手工编程是比较复杂的,对编程者的数学基础要求较高。
文中主要以椭圆为例来介绍非圆曲线数学模型的建立与编程加工。
一、前言在数控车床加工中,非圆曲线工件的手工编程,要求编程者对数控原理非常熟悉,且要有一定的数学功底。
二、编程方法非圆曲线工件的手工编程,有两种方法,一是用圆弧逼近法或直线逼近法编程;二是用用户宏程序编程。
三、用圆弧逼近法或直线逼近法编程1.工件装夹如图1所示,在数控车床上直接用三爪卡盘装夹,为了方便对刀和编制程序,将程序原点设定在工件的右侧中心线上。
图1 椭圆2.数学模型工件右边部分为标准椭圆,长轴半径为20,短轴半径为14,所以标准方程为:Z 2/202+X 2/162=1在Z 轴上负向取点,通过椭圆方程计算出各点坐标如表所示。
3.参考程序(椭圆的精车程序)用车锥法粗车椭圆(程序略),用直线逼近法精车椭圆,程序如下。
O0001;N5 G90G97T0101;设定刀具号及刀具补偿号N10 M03 S1200; 设定转速及转向N15 G00X30Z5; 设定加工起点N20 X0;N25 G01X0Z0F0.1;精加工椭圆N30 X0.88Z-0.01;N35 X1.25Z-0.02;N40 X1.979Z-0.05;N45 X2.796Z-0.1;N50 X3.423Z-0.15;N55 X3.950Z-0.2;N60 X4.832Z-0.3;N65 X5.572Z-0.4;N70 X6.222Z-0.5;N75 X6.807Z-0.6;N80 X7.343Z-0.7;表 各点坐标N85 X7.84Z-0.8;N90 X8.305Z-0.9;N95 X8.743Z-1;N100 X9.55Z-1.2;N105 X10.29Z-1.4;N110 X10.974Z-1.6;N115 X11.610Z-1.8;N120 X12.205Z-2;N125 X13.805Z-2.6;N130 X14.750Z-3;N135 X15.617Z-3.4;N140 X16.225Z-3.7;N145 X16.8Z-4;N150 X17.695Z-4.5;N155 X18.520Z-5;N160 X19.285Z-5.5;N165 X19.996Z-6;N170 X20.659Z-6.5;N175 X21.278Z-7;N180 X21.857Z-7.5;N185 X22.4Z-8;N190 X22.908Z-8.5;N195 X23.385Z-9;N200 X23.831Z-9.5;N205 X24.249Z-10;N210 X24.640Z-10.5;N215 X25.005Z-11;N220 X25.662Z-12;N225 X26.229Z-13;N230 X26.710Z-14;N235 X27.111Z-15;N240 X27.434Z-16;N245 X27.683Z-17;N250 X27.860Z-18;N255 X27.965Z-19N260 X28Z-20;N265 X27.860Z-22;N270 X27.683Z-23;N275 X27.434Z-24;N280 X27.111Z-25;N285 X26.710Z-26;N290 X26.229Z-27;N295 X25.662Z-28;N300 X25.005Z29;N305 X24.640Z-29.5;N310 X24.249Z-30;N315 Z-31;N320 G00X30;N325 X100Z100; 快速回到换刀点N330 M05; 转速停止N335 M30; 程序结束返回程序号四、用用户宏程序编程1.以Z坐标作为变量(1)工件装夹。

数控车椭圆编程与加工方法探讨随着科技的不断发展,数控技术在机械制造领域得到了广泛的应用。
数控车床作为数控机床的一种,以其高效、精确、稳定等特点,在各种生产场合中广泛使用。
数控车椭圆编程与加工是数控车床的一项重要技术,本文将对这一技术进行探讨。
首先,我们需要了解什么是椭圆。
椭圆是一种特殊的二次曲线,其方程通常为(x^2/a^2+y^2/b^2=1),其中a为长轴的一半,b为短轴的一半。
基于该方程,我们可以得到数控车椭圆编程与加工需要用到的参数,如长轴、短轴、角度、起点、终点等。
其次,我们需要了解数控车椭圆编程的基本方法。
数控车椭圆编程可以采用G02/G03指令来进行,G02指令用于绘制逆时针方向的椭圆,G03指令用于绘制顺时针方向的椭圆。
具体来说,数控车椭圆编程需要设置下述几个重要参数:1. 椭圆的长轴a和短轴b;2. 椭圆的起点和终点坐标;3. 椭圆的中心点坐标;4. 椭圆的绘制方向(顺时针或逆时针);5. 插补精度。
在编写数控车椭圆程序时,我们需要以椭圆中心点为原点建立坐标系,并根据椭圆的长轴和短轴计算出各个点的坐标,再将这些点传入控制系统中,通过插补算法计算出每一个插补点的速度和位置,最终实现椭圆的绘制。
最后,我们需要了解数控车椭圆加工的工艺。
首先,在加工前需要进行加工零件的定位和夹紧。
接着,根据椭圆的长轴和短轴计算出加工刀具的路径和加工速度。
在加工过程中,要注意加工刀具的进刀深度、切削速度和冷却液的使用,以确保加工质量和刀具的寿命。
当加工完成后,要对加工零件进行检查和测量,以验证尺寸精度和表面质量是否达到要求。
综上所述,数控车椭圆编程与加工是一项技术含量较高、技术难度较大的工艺。
在操作数控车椭圆编程时,我们不仅需要具备深厚的数控知识和编程经验,还需要了解椭圆的数学原理以及加工工艺的各种细节。
只有通过不断实践和总结,才能真正掌握这一技术,并为机械制造业的发展做出贡献。
椭圆宏程序在数控车床加工的方法椭圆宏程序的基本原理是利用圆的特性来实现椭圆形的加工。
椭圆是一种圆的特殊形式,其变形是通过改变加工过程中的切削刀具的移动轨迹来实现的。
椭圆宏程序通过数学计算和编程实现刀具的移动轨迹变化,从而实现椭圆形的加工。
1.定义椭圆的参数:椭圆的形状可以通过两个半径参数来定义,分别为长半径和短半径。
这些参数可以根据零件的要求进行调整。
2.计算椭圆的切削路径:通过数学计算,可以确定刀具在加工过程中的移动轨迹。
这个轨迹是一个连续而光滑的曲线,可以通过数学公式或计算机模拟来得到。
3.编写椭圆宏程序:根据计算所得的切削路径,编写相应的宏程序。
宏程序是一种特殊的程序,可以在数控机床上执行。
它包含了一系列指令,用于控制刀具的移动、切削深度等参数。
4.设定加工参数:在执行宏程序之前,需要将一些重要的加工参数进行设定。
这些参数包括切削速度、进给速度、切削深度等。
它们的选择需要根据材料的性质和要求进行调整。
5.执行宏程序:当所有参数设置完成后,就可以执行宏程序了。
数控机床会按照宏程序中定义的指令和轨迹来进行切削,从而实现椭圆形的加工。
椭圆宏程序的优点是可以高效地制造复杂形状的椭圆零件。
相比于传统的手工加工或其他编程方法,椭圆宏程序的精度更高,生产效率更高。
此外,它还具有良好的可编程性和易于调整的特点,可以适应不同类型的椭圆加工需求。
总结起来,椭圆宏程序是一种用于数控车床加工的方法,通过定义椭圆参数、计算切削路径、编写宏程序以及设定加工参数等步骤来实现椭圆形的加工。
它能够提高零件的精度和质量,提高生产效率,适用于制造复杂形状的椭圆零件。
数控车床加工椭圆的方法
摘要本文讲述在数控车床上利用椭圆直角坐标和极坐标方程,通过对宏程序进行编程来加工椭圆,同时总结了针对不同尺寸规格椭圆的编程方法。
关键词数控车床;加工椭圆;方法
1概述
二维轮廓的椭圆形零件在日常生活中使用得非常多,尤其是在机械制造业中更是应用广泛,但是,该零件加工起来的难度是非常大的。
椭圆形零件的加工方法有很多种,比较常见的有以下几种:在普通车床上进行近似加工[1];根据椭圆的形成原理,设计专用的加工装置进行加工[2];在数控车床上利用“虚拟轴”原理实现椭圆曲线的数控加工[3];利用圆弧逼近法[4]、直线逼近法加工等。
本文仅讨论利用直线逼近法(宏程序)加工椭圆。
2直线逼近法
现今,计算机和自动化技术发展迅速,数控车床相关技术也随之不断进步,给椭圆形截面零件的加工创造了很好的条件。
从目前的技术来说,各种数控车床进行椭圆加工的插补原理基本相同,不同的是实现插补运算的方法。
圆弧插补与直线插补是两种常用的实现插补运算的方法,但是目前还没有椭圆插补。
因为受到各方面的限制,尤其在设备和条件方面,通常我们无法手工来编制程序,必须借助于电脑来实现。
一般来说,通过拟合运算及直线逼近法编写宏程序来加工椭圆。
宏程序指令适用于抛物线、双曲线、椭圆等没有插补指令的非圆曲线编程;还适用于图形相同,只是尺寸不同的一系列零件编程,同样还适用于工艺路线一样,只是位置数据不同的系列零件的编程。
相比于其他编程方法,宏程序实现椭圆形截面零件的加工的优点在于,其能有效的简化程序,提高程序的运行速度,并且能扩展数控机床的使用范围。
3用户宏程序法
数控车床通过程序来实现某项功能,将编写的程序存储在数控车床中,并将这些实现某项功能的程序用某个简单命令代表,利用数控车床进行加工时,只需要写入代表命令就可以执行相应的功能,极大的减少了操作流程,提高了工作效率。
其中,把存入数控机床的一组程序称作用户宏程序主体,简称为宏程序;把代表命令称作用户宏程序命令,简称为宏命令。
这样,工作人员操作数控车床时,只需记忆实现某项功能的宏命令即可,不需要记忆繁琐的宏程序。
能够进行变量间的相互运算是宏程序的最大优点。
利用宏命令能够把实际值赋予某个变量,利用数控车床加工椭圆的过程中,可以通过间接幅值和直接幅值的方式对宏程序中的变量进行赋值。
1)直接赋值:使变量直接等于即时值或某项数值的方法。
#1=55(表示变量#1等于55)
#2=#3(表示变量#2等于#3的值)
2)间接赋值:就是用演算式赋值,即把演算式内演算的结果赋于某个变量。
如图1所示,车削1/4椭圆的回转轮廓曲线。
车削从点A到点B,采用直线逼近法在Z向分段,以0.2mm(0.5度)为一个步距,就可以编制一个只用变量不用具体数据的椭圆,不必更改宏程序,而只要修改主程序中宏指令段内的赋值数据就可以.现利用椭圆的直角坐标方程和极坐标方程来编制宏程序。
4 利用椭圆直角坐标方程编制宏程序
直角坐标标准方程为:
其中a为椭圆短轴(a=15),b为椭圆长轴(b=30)
编制参考程序如下:(以FANUC Series 0i Mate-TC数控系统为例)
(毛坯φ62mm)
O0001;
N10 G98 G21 F200;
N20 T0101;
N30 M03 S800;
N40 G00 X65 Z35;
N50 G73 U30 R15;
N60 G73 P70 Q140 U0.3 W0;
N70 #1=30;(Z轴起始位置)
N80 #2=30;(椭圆长轴半径)
N90 #3=15;(椭圆短轴半径)
N100 #4=#3*SQRT [1-(#1*#1)/(#2*#2)];(椭圆短半轴变量数值)
N110 G01 X(2*#4)Z(#1)F200;(椭圆插补)
N120 #1=#1-0.2;(Z轴步距)
N130 IF(#1 GE 0 ) GOTO 110;(符合条件,则跳转到N110程序段)N140 U2;
N150 G70 P70 Q140 S1000 F100;
N160 G00 X100;
N170 Z150;
N180 M05;
N190 M30;
5 利用椭圆极坐标方程编制宏程序
椭圆极坐标方程为:X = B*SI Nα
Z = A*COSα(0°≤α≤90°)
其中A为椭圆长轴(A=15),B为椭圆短轴(B=30)
编制参考程序如下:(以FANUC Series 0i Mate-TC数控系统为例)(毛坯φ62mm)
O0001;
N10 G98 G21 F200;
N20 T0101;
N30 M03 S800;
N40 G00 X65 Z35;
N50 G73 U30 R15;
N60 G73 P70 Q140 U0.3 W0;
N70 #1=30;(椭圆长轴半径)
N80 #2=15;(椭圆短轴半径)
N90 #4=0; (椭圆起始角度)
N100 G01 X [#2*SIN(#4)] Z [#1*COS(#4)] F200;(椭圆插补)
N110 #4=#4+0.5;(角度变量)
N120 IF(#4 LE 90 ) GOTO 100;(符合条件,则跳转到N100程序段)
N130 U2;
N140 G00 X100;
N150 Z150;
N160 M05;
N170 M30;
在上述两例中可以看出,这是两个通用的椭圆加工宏程序,只要改变起刀点的坐标及A(a)、B(b)三个赋值,便可加工任意椭圆。
同时,我们也可以看到Z轴步距和角度每次增加的大小和最后工件的加工表面质量有较大关系,即记数器的每次变化量与加工的表面质量和效率有直接关系。
希望读者在实际应用中注意。
6结论
随着我国经济的发展和科学文化水平的提高,数控车床取得飞速发展,数控车床具有加工精度高、加工质量高和加工范围广等优点,其发展潜力不容小觑。
利用传统车床加工椭圆的方法比较复杂,不容易实现,但是采用数控车削法可以相对容易的解决非圆截面加工难题,提高加工效率,为企业创造更多的经济效益。
参考文献
[1]刘晓初.一种在机床上加工椭圆零件的近似方法.机械制造,1998(2).
[2]张增林,等.椭圆、摆线形成定理及加工装置的设计.机械设计,1994(3).
[3]邱继红.数控机床加工椭圆曲线的一种新编程法.组合机床与自动化加工
技术,1999(4).
[4]徐守敬.数控车床加工椭圆的技术探讨.机械制造,2006(9).
[5]瞿瑞波主编.数控机床编程与操作.北京:中国劳动社会保障出版社,2006.
[6]北京发那科机电有限公司BEIJING-FANUC 操作编程说明书.北京发那科机电有限公司.
[7]孙竹编著.数控机床编程与操作.机械工业出版社,1996.
[8]李平惠,李爽立.浅谈数控车床加工椭圆.科技信息,2010(11X).
[9]钱萍.数控车床加工正椭圆曲线的编程方法.农业装配技术,2009(6).。