无损耗均匀传输线方程的通解.
- 格式:ppt
- 大小:180.00 KB
- 文档页数:10
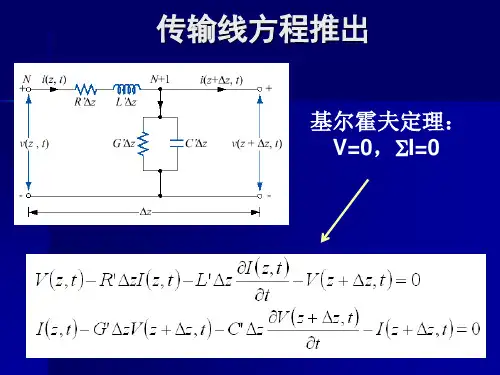





均匀传输线方程及其解
哎哟,说到这个均匀传输线方程嘛,可是咱们工程界里头的一个大头哦。
先给大家说说这方程是个啥玩意儿,然后再慢慢儿地给大家展开讲讲咋解。
咱们先从陕西话儿说起,这均匀传输线方程啊,就像是咱老陕地里的那条直溜溜儿的渠,水流稳稳当当地过去,不歪不斜。
这方程嘛,就是描述那条“水流”——也就是信号——在传输线上是怎么跑的。
再换到咱们四川话儿,这方程就像咱们四川的麻辣烫,各种调料都得恰到好处,多了少了都不行。
信号在传输线上跑,也得有个“度”,快了慢了都会影响效果。
那咋解这方程呢?这可得好好儿说说。
解这方程啊,就像咱们做川菜一样,得一步一步来,不能急。
首先得把方程里的各个量都弄清楚,哪些是已知的,哪些是未知的,这就好比咱们做菜前要准备好的各种食材。
然后就开始动手解啦。
这解的过程啊,有时候得用点儿小技巧,就像咱们川菜厨师炒菜时用的那些独门绝技。
有时候得加点儿这个,减点儿那个,才能让味道刚刚好。
解完之后呢,还得检查一下解得对不对。
这就像咱们做完菜后要尝尝味道一样,看看符不符合要求。
所以说啊,这均匀传输线方程及其解,虽然听起来挺复杂的,但只要咱们用心去做,就一定能把它搞明白。
就像咱们做菜一样,只要用心去做,就一定能做出美味佳肴来。

§14.5 无损耗传输线14.5.1 无损耗传输线的特点如果传输线的电阻0R 和导线间的漏电导0G 等于零,这时信号在传输线上传播时,其能量不会消耗在传输线上,这种传输线就称为无损耗传输线,简称无损耗线。
当传输线中的信号的ω很高时,由于00R L >>ω、00G C >>ω,所以略去0R 和0G 后不会引起较大的误差,此时传输线也可以被看成是无损耗线。
因为00=R ,00=G ,所以无损耗传输线的传播常数γ000000))((C L j C j L j Y Z ωωωγ===即0=α,00C L ωβ=,可见无损耗线也是无畸变线。
无损耗传输线的特性阻抗c Z 为00C L Y Z Z c ==为纯电阻性质的。
因为0=α,所以依式(14-8)可知无损耗线上的电压和电流相量为)sin()cos()sin()cos(2222x Z U j x I I x I jZ x U U cc '+'='+'=ββββ (14-10) 其中x '为传输线上一点到终端的距离。
从距终端x '处向终端看进去的输入阻抗为c c cin Z x jZ x Z x jZ x Z I U Z )sin()cos()sin()cos(22'+''+'==ββββ (14-11)其中,222I UZ =为终端负载的阻抗。
14.5.2 终端接特性阻抗的无损耗线当传输线的终端阻抗与传输线相匹配,即c Z Z =2时,由式(14-10)可求得无损耗线上的电压和电流相量为x I x j x I x Z U j x I I x U x j x U U x I jZ x U U cc '∠='+'='+'='∠='+'='+'=ββββββββββ22222222)]sin()[cos()sin()cos()]sin()[cos()sin()cos(其电压、电流的时域表达式为)sin(2)sin(22222i u x t I i x t U u ϕβωϕβω+'+=+'+=其中,2u ϕ和2i ϕ分别为终端电压和电流的初相。

实数,单位:Ω常数,单位:m/s
单位:m
n U += 终端反射系数
任一点的反射系数
Z
结论
①入端阻抗和传输线的特性阻抗、工作频率、传输线
讨论
结论
路情况下的入端阻抗,可以计算出该传输线的特性阻抗
特点
驻波特点
电压沿
线作余
弦分布
x'
驻波比(SWR )的含义:
驻波比是一个数值,用来表示天线和电波发射台是否匹配。
如果SWR 的值等于1,则表示发射传输给天线的电波没有任何反射,全部发射出去,这是最理想的情况。
如果SWR大于1,则表示有一部分电波被反射回来,最终变成热量,使得馈线升温。
被反射的电波在发射台输出口也可产生相当高的电压,有可能损坏发射台。

均匀传输线知识介绍目录:1.1分布参数电路1.2均匀传输线及其方程1.3均匀传输方程的正弦稳态解1.4均匀传输线的原参数和副参数1.5无损耗传输线1.6无损耗传输线方程的通解1.7无损号线的波过程1.8习题均匀传输线—内容摘要—本章首先介绍分布参数电路的概念和均匀传输线。
其次讨论均匀传输线的方程及其正弦稳态解,沿线电压和电流分布情况,引入行波入射波反射波等概念吗,并介绍均匀传输线的副参数特性阻抗和传播常数等概念。
讨论了无损耗现在终端开路和短路情况下电压和电流的驻波及其输入阻抗的特点。
最后,简要介绍了无损耗线的波过程。
分布参数电路在以前各章中吗,讨论了由集总参数元件组成的电路模型。
每一种集总参数元件被假设集中由一种电磁现象所表征。
例如,电阻元件集中表征了某一个实际部件或某一段实际电路中的能量消耗,电感元件集中地反映了磁场的物理现象(如充、放电,位移电流等)。
但是,在某些实际电路中,发生的电磁现象往往是带有分布性的,必须在一定条件下才能建立起集总参数模型。
导线中的电流由导线中电场产生的,电流在导线外产生磁场;并且由于两导线之间的电压,导线间也有电场,此电场在导线间产生电容电流和漏电流。
这些电场—磁场都是沿线分布,及分散在空间的。
就到线上的能量损耗与磁场效应来说,因导线间的电流导致导线中的电流处处不同,故不能以一项i2r或ldi/dt来概括导线上的物理过程;而到线上的电阻、电感压降也导致导线间的电压处处不同,故不能以一项u2g或cdu/dt来概括导线间的物理过程。
接近这种物理现象的电路模型,应是有无限多个导线上的电阻、电感以及无限多个导线间的电导、电容所组成的分布参数模型。
应当说,任何实际电路都有是否必须采用分布参数模型的问题。
以传输线为例,只要沿线流动电流的电流随空间变化很小,及导线间的空间电容电流及颠倒电流不太大时,就可以用单个电阻来描写损耗、单个电感来描写磁场作用。
引申至一个实际电阻器的情况,在直流工作条件下其模型仅为一个电阻元件,在低频交流工作条件下其模型则是电阻元件的串联组合;另一方面,当可以不记导线上电阻、电感电压降时,认为导线间所有漏电流、所有电容电流处于同一个电压时,就可以用单个点到来描述导线间漏电作用、单个电容来描述导线间的电流的电阻性压降,其模型就是一个电容元件和电导元件的并联组合。