3.12用解析穷举法解决问题2

4.1—4.2 用解析法、穷举法设计程序【学习目标：】1、理解解析法和穷举法2、分清两者之间的区别在经过大量编程实践之后，人们总结出很多行之有效的算法来解决实际问题。

常用的方法有：解析法、穷举法、查找法、排序法、递归法等。

4.1 解析法所谓解析法是指：通过分析问题中各要素之间的关系，用最简练的语言或形式化的符号来表达它们的关系，得出解决问题所需的表达式，然后设计程序求解问题的方法。

例1：求三角形面积已知a、b、c分别为三角形的三条边长，利用海伦公式求该三角形面积p=(a+b+c)/2编程实现：输入边长a，b，c，如果能构成三角形，输出面积，否则输出“No Answer!”界面如下：Dim a As Single , b As Single , c As Singlea=val(text1.text)b=val(text2.text)c=val(text3.text)If thenp=(a+b+c)/2s=sqr(p*(p-a)*(p-b)*(p-c))text4.text=format(s,”0.00”) ‘结果保留两位小数Elsetext4.text=”no answer”End If根据上述回答下列问题（8分，每空4分）（1）、利用海伦公式求三角形面积的算法是_____（解析法/查找法/枚举法/排序法）。

（2）、填写出参考程序中空白处的表达式________（填写字母：A/B/C/D）A、a + b > c or a + c > b and b + c > aB、a + b > c or a + c > b or b + c > aC、a + b > c and a + c > b or b + c > aD、a + b > c and a + c > b and b + c > a（1）解析法（2）D用解析法求解问题，许多时候并非只是计算一个解析式就可以完事，还要根据问题给出的已经条件，运用归纳、演绎等逻辑方法，揭示问题各要素之间的关系，寻找表示这种关系的表达式，有时需要计算的解析式是一组而不仅仅是一条。

穷举算法及解题穷举算法及解题例12-1 古希腊人认为因子的和等于它本身的数是一个完全数（自身因子除外），例如28的因子是1、2、4、7、14，且1+2+4+7+14=28，则28是一个完全数，编写一个程序求2~1000内的所有完全数。

问题分析（1）本题是一个搜索问题，搜索范围2~1000，找出该范围内的完全数；（2）完全数必须满足的条件：因子的和等于该数的本身；（3）问题关键在于将该数的因子一一寻找出来，并求出因子的和：分解因子的方法比较简单，采用循环完成分解因子和求因子的和。

程序如下：program p12_1;var a,b,s:integer;beginfor a:=2 to 1000 dobegins:=0;for b:=1 to a-1 doif a mod b =0 then s:=s+b;if a=s then beginwrite(a,'=',1,);for b:=2 to a-1 doif a mod b=0 then write('+',b);writeln;end;end;end.当程序运行后,输出结果:6=1+2+328=1+2+4+7+14496=1+2+4+8+16+31+62+124+248例12-3邮局发行一套票面有四种不同值的邮票,如果每封信所帖邮票张数不超过三枚,存在整数r,使得用不超过三枚的邮票,可以贴出连续的整数1、2、3、……、r来，找出这四种面值数，使得r值最大。

问题分析：本题则是知道每封信邮票数的范围(<=3),邮票有四种类型，编程找出能使面值最大邮票。

其算法是：(1) 面值不同的四种邮票，每封信所贴邮票不超过3张；(2) 用这四种邮票贴出连续的整数，并且使r值最大；(3) 用穷举法，找出所有符合条件的解；(4) 本题用集合的方法统计邮票的面值，提高判重的速度。

设四种邮票的面值分别为：a,b,c,d,根据题意设：a<b<c<d,因此a=1,用循环语句完成搜索。

穷举法算法案例穷举法，又称为暴力搜索或者暴力破解，是一种简单直接的算法，它通过尝试所有可能的情况来寻找问题的解。

虽然在某些情况下效率不高，但在一些小规模问题或者需要精确解的情况下，穷举法仍然是一个有效的解决方案。

下面我们将通过几个案例来了解穷举法的具体应用。

案例一，寻找素数。

素数是指除了1和自身外没有其他因数的自然数，例如2、3、5、7等。

我们可以通过穷举法来寻找一定范围内的所有素数。

具体做法是从2开始，依次判断每个数是否能被2到该数平方根之间的所有数整除，如果不能则该数是素数。

这种方法虽然效率不高，但对于小范围内的素数搜索是可行的。

案例二，密码破解。

在密码学中，穷举法常常被用来破解简单的密码，例如暴力破解4位数字密码。

假设密码由0-9的数字组成，那么一共有10000种可能的密码组合。

通过穷举法，我们可以依次尝试每一种组合，直到找到正确的密码。

当然，对于更复杂的密码，穷举法可能需要花费更长的时间，但在一些情况下仍然是有效的。

案例三，旅行推销员问题。

旅行推销员问题是一个经典的组合优化问题，假设有n个城市，推销员需要从某个城市出发，经过每个城市一次，最终回到出发的城市，要求找到一条最短的路径。

穷举法可以用来解决这个问题，具体做法是列举出所有可能的路径，计算它们的长度，最终找到最短的路径。

虽然对于大规模的问题来说，穷举法并不是最优的解决方案，但在小规模问题上仍然是可行的。

总结。

穷举法作为一种简单直接的算法，在一些情况下仍然具有一定的应用价值。

然而，需要注意的是，穷举法在处理大规模问题时可能会面临效率低下的问题，因此在实际应用中需要根据具体情况选择合适的算法。

希望通过上述案例的介绍，能够让大家对穷举法有一个更加深入的了解。

程序填空题一1. 下面C语言程序将两个递增有序的数值a和b 合并一个数组c,并保持递增次序，最后输出数组c.#include < stodio.h>#define M6#define N5main( ){int a[M]={1,3,5,7,9,11} b[N]={2,4,6,8,10}int c[M+N]int i ,j, k;i=j=k=0while( 1 )if a[i]<b[j]c[k++]=a[i++];else c[k++]=b[j++];while( 2 )c[k++]=a[i++];while(j<N)c[k++]=( 3 )for(k=0;k<( 4 );k[++])printf(%dxt,c[k]; ）其中（1）（2）（3）（4）处分别填一数据，使程序达到其功能。

答案:1:i<M&&j<N2:i<M;3:b[j++];4:M+N2．下面h函数的功能是计算如下数学函数H的值。

请填空。

double fgh（double（*f）（double a），double （* g）（double b），double x，double y）{return（【1】）；}double h（double a，double b）return（fgh（sin，cos，a，b）* fgh（【2】））；}解：（1）（*f）（x＋y）/（*g）（y－x）（2）cos，sin，a，b[解析]本题考察的是函数的声明。

要填写的两个空都出现在return语句中，所以要仔细分析函数的返回值。

本题的第二个空相对要容易一些，只要根据题干和乘号前面的调用语句对比一下即可得到调用语句的四个参数。

第一个空相对要难一些，函数fgh定义时用到了函数指针（*f）和（*g）是为了增加函数的灵活性。

根据函数h的定义以及题干要求，可以看出函数fgh应该表示的是乘号两边的某一项。

用列举法解决问题解决问题的方法有很多种，而列举法便是其中之一。

通过列举法可以将问题分解成多个具体的部分，从而更容易找到解决方案。

本文将以列举法为主题，介绍如何使用列举法来解决问题。

首先，列举法要求我们将问题进行分类，将问题分解成多个小问题。

通过对每个小问题进行独立的思考和解决，最终可以得到整体问题的解决方案。

举个例子，假设我们面临着一个时间管理的问题。

首先，我们可以将时间管理问题分解成几个方面，比如学习时间的管理、工作时间的管理、娱乐时间的管理等等。

然后，我们再逐个解决每个方面的问题，比如制定学习计划、合理安排工作时间、明确娱乐时间的合理范围等等。

其次，列举法还可以通过具体的例子来寻找问题的解决方法。

通过列举与问题相关的实例，我们可以更清楚地了解问题的本质和特点，从而更容易找到解决方法。

例如，假设我们面临着一个环保问题，我们可以列举与该问题相关的实例，比如大气污染、水污染、垃圾处理等等。

通过对每个实例进行分析和研究，我们可以找到解决问题的方法，比如加强环保意识、推动可持续发展等等。

此外，列举法还可以通过比较不同的方案来找到最合适的解决方法。

我们可以列举出多种解决问题的方案，并进行评估和比较，找到最适合自己的解决方案。

例如，假设我们需要选择一种健身方法来保持身体健康，我们可以列举出跑步、游泳、瑜伽等不同的健身方式。

然后，我们可以对每种方式进行评估，比较它们的优缺点，从而找到最适合自己的健身方法。

最后，列举法还可以通过寻找事实和证据来解决问题。

我们可以通过列举相关的事实和证据，来支持我们的观点和解决方案。

例如，如果我们要解决城市交通拥堵问题，我们可以列举相关的数据和研究结果，来说明交通拥堵的原因和解决方法。

通过事实和证据的支持，我们的解决方案更加具有说服力和可行性。

总结起来，列举法是一种解决问题的有效方法。

通过将问题分解成多个小问题、通过具体的例子和比较不同的方案、通过寻找事实和证据等方式，我们可以找到更合适的解决方法。

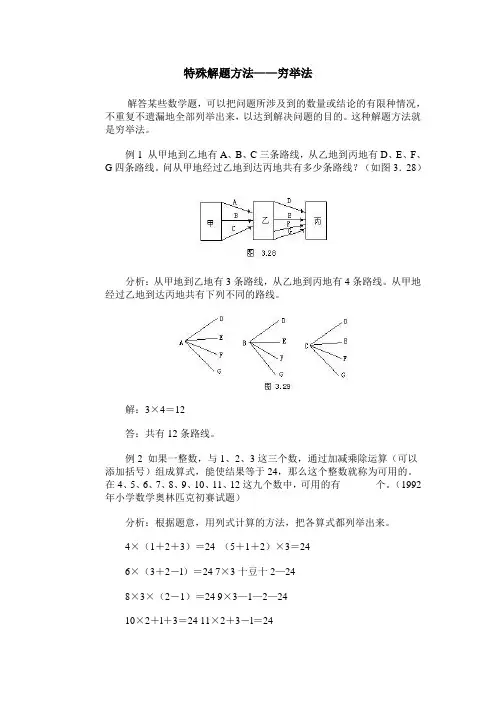
特殊解题方法——穷举法解答某些数学题，可以把问题所涉及到的数量或结论的有限种情况，不重复不遗漏地全部列举出来，以达到解决问题的目的。

这种解题方法就是穷举法。

例1 从甲地到乙地有A、B、C三条路线，从乙地到丙地有D、E、F、G四条路线。

问从甲地经过乙地到达丙地共有多少条路线？（如图3．28）分析：从甲地到乙地有3条路线，从乙地到丙地有4条路线。

从甲地经过乙地到达丙地共有下列不同的路线。

解：3×4＝12答：共有12条路线。

例2 如果一整数，与1、2、3这三个数，通过加减乘除运算（可以添加括号）组成算式，能使结果等于24，那么这个整数就称为可用的。

在4、5、6、7、8、9、10、11、12这九个数中，可用的有_______个。

（1992年小学数学奥林匹克初赛试题）分析：根据题意，用列式计算的方法，把各算式都列举出来。

4×（1＋2＋3）＝24 （5＋1＋2）×3＝246×（3＋2－l）＝24 7×3十豆十2—248×3×（2－1）＝24 9×3—1—2—2410×2＋l＋3＝24 11×2＋3－l＝2412×（3＋1－2）＝24通过计算可知，题中所给的9个数与1、2、3都能够组成结果是24的算式。

答：可用的数有9个。

例3 从0、3、5、7中选出三个数字能排成_______个三位数，其中能被5整除的三位数有_________个。

（1993年全国小学数学竞赛预赛试题）分析：根据题中所给的数字可知：三位数的百位数只能有三种选择：十位数在余下的三个数字中取一个数字，也有3种选择；个位数在余下的两个数字中取一个数字，有2种选择。

解:把能排成的三位数穷举如下，数下标有横线的是能被5整除的。

305，307，350，357，370，375；503，507，530，537，570，573；703，705，730，735，750，753答：能排成18个三位数，其中能被5整除的有10个数。

第五节、用穷举法求解问题课题：第五节、用穷举法求解问题【教学目标】l知识与技能1) 知道什么是穷举法。

2) 理解穷举算法的基本特征。

1)通过体会一个具体实例的解法，能用自己的语言概括和归纳穷举法的概念及特点。

2)通过小组讨论交流，找出使用穷举法解决具体问题的要点并将流程图补充完整。

l情感态度与价值观1) 体会算法与实际生活的紧密联系，增强学习算法的兴趣。

2) 愿意与同伴交流自己的想法，并共同完成算法的设计。

【教学重点】l掌握用穷举法解决实际问题的基本思想方法。

【教学难点】l发现并用流程图实现生活中的穷举法算法问题。

【教学过程】一、导入：1、问题情景：教师：某天早上，英语课代表收好了英语练习本，他的同桌语文课代表收好了语文练习本，但是由于一些意外，两种练习本混在了一起。

现在要把混在一起的102本练习本区分开，假如你是英语课代表，你会做？学生：通过思考寻找解决问题的方法。

教师：找两名同学谈谈解决思路。

2、分析教师：引导学生整理思路，并出示解决上述问题的流程图，（引导时，教师要强调研究范围为102本作业，每一本作业都要逐一检验，分成两类所需的判断条件），为下面的概括穷举法做好铺垫。

可能的引导性提问：每次要做的事情是什么？要做多少次？作业本需要重复检验吗？分成两类的标准是什么？然后教师将流程图加以抽象概括，将穷举法的核心步骤抽象成“列举”和“检验”两个部分。

学生：观察流程图，并对比反思自己的想法，初步体会穷举法。

3、引出课题：穷举法教师：鼓励学生相互讨论，然后尝试用自己的话概括什么是穷举法。

如果学生概括的有欠缺，教师可以先加以点拨，用反问法，如：刚才那道题目检验的次数为什么要限制在102个练习本？（限定范围）每个作业本用不用反复检查啊？（逐个检验，是指每一个对象检验一遍），最后出示穷举法的定义。

4、“穷举法”的定义教师：出示“穷举法”的定义：这种列举出所有可能的情况并逐一进行检验，根据检验的结果执行相应操作的方法就是穷举法。

穷举法求解简单计算问题根据问题的已知条件，对影响答案的各种因素可能的取值范围进行组合，在所有可能的组合情况中筛选出满足条件的答案。

一般，影响答案的各种因素作为循环变量，用多重循环对各种因素进行组合，在内层循环中验证每种组合并输出满足条件的答案。

2-1. 编程，输出20以内（含20）所有满足C2=A2+B2的完全平方数C。

分析：影响答案的因素有A、B、C，它们的取值范围均为1～20。

所以用三重循环穷举A、B、C可能的值，输出满足条件C2=A2+B2的C、A、B及C的个数。

main( ){ long a,b,c,n=0;for(c=1;c<=20;c++)for(a=1;a<=20;a++)for(b=1;b<=20;b++)if(c*c==a*a+b*b)printf("%ld %ld %ld\n",c,a,b);}2-2. 一辆卡车违犯交通规则，撞人逃跑。

现场三人目击事件，但都没记住车号，只记下车号的一些特征。

甲说：牌照的前两位数字是相同的;乙说：牌照的后两位数字是相同的;丙是位数学家，他说：四位的车号刚好是一个整数的平方。

根据以上线索，编程，输出车号。

分析：用两重循环构造一个前两位数相同、后两位数相同整数i*1000+i*100+j*10+j，（其中i=1～9，j=0～9），然后再用循环（c=31～99,c的平方为4位数）判断该整数是否是c的平方。

2-3．用40元买苹果、西瓜和梨共100个，3种水果都要。

已知苹果0.4元一个，西瓜4元一个，梨0.2元一个。

问可以各买多少个？编程，输出全部购买方案。

分析：设西瓜买x个,苹果买y个,梨买z个,则问题满足方程：4x+0.4y+0.2z=40x+y+z=100即: 40x+4y+2z=400x+y+z=100西瓜至多买(40-0.4-0.2)/4=9 个, 苹果至多买(40-4-0.2)/0.4=89 个,梨买100-y-z个.用两重循环（x=1～9,y=1～89）输出满足条件x+y+z =100和40x+4y+2z=400的所有购买方案。