2020年高中物理竞赛习题专题十一：几何光学(Word版含解析)

几何光学测试题1、如图（a ）所示，一细长的圆柱形均匀玻璃棒，其一个端面是平面（垂直于轴线），另一个端面是球面，球心位于轴线上．现有一很细的光束沿平行于轴线方向且很靠近轴线人射．当光从平端面射人棒内时，光线从另一端面射出后与轴线的交点到球面的距离为a ；当光线从球形端面射人棒内时，光线在棒内与轴线的交点到球面的距离为b ．试近似地求出玻璃的折射率n 。

2、内表面只反射而不吸收光的圆筒内有一半径为R 的黑球，距球心为2R 处有一点光源S ，球心O 和光源S 皆在圆筒轴线上，如图所示．若使点光源向右半边发出的光最后全被黑球吸收，则筒的内半径r 最大为多少？3、如图1中，三棱镜的顶角α为60︒，在三棱镜两侧对称位置上放置焦距均为 30.0cm f =的两个完全相同的凸透镜L 1和 L 2．若在L 1的前焦面上距主光轴下方14.3cm y =处放一单色点光源S ，已知其像S '与S 对该光学系统是左右对称的．试求该三棱镜的折射率．4、如图（a ）所示，两平面镜A 和B 的镜面分别与纸面垂直，两镜面的交线过图中的O 点，两镜面间夹角为︒=15α，今自A 镜面上的C 点处沿与A 镜面夹角︒=30β的方向在纸面内射出一条光线，此光线在两镜面经多次反射后而不再与镜面相遇。

设两镜面足够大，1=CO m 。

试求：（1）上述光线的多次反射中，最后一次反射是发生在哪块镜面上？ （2）光线自C 点出发至最后一次反射，共经历多长的时间？5、有一水平放置的平行平面玻璃板H ，厚3.0 cm ，折射率 1.5n =。

在其下表面下2.0 cm 处有一小物S ；在玻璃扳上方有一薄凸透镜L ，其焦距30cm f =，透镜的主轴与玻璃板面垂直；S 位于透镜的主轴上，如图（a ）所示。

若透镜上方的观察者顺着主轴方向观察到S 的像就在S 处，问透镜与玻璃板上表面的距离为多少?6、望远镜的物镜直径D ＝250cm ，其焦距f ＝160m 。

高中物理《几何光学》练习题（附答案解析）学校:___________姓名：___________班级：_____________一、单选题1．下列说法正确的是（）A．光纤通信是光的色散的应用P原子核经过一个半衰期后，一定剩下4个没有衰变的原子核B．8个3015C．原子核的比结合能越大，原子核就越稳定D．光的干涉、衍射现象证实了光具有波动性，偏振现象证实光是纵波2．如图甲所示，每年夏季我国多地会出现日晕现象，日晕是太阳光通过卷层云时，发生折射或反射形成的。

一束太阳光射到截面为六角形的冰晶上发生折射，其光路图如图乙所示，a、b为其折射出的光线中两种单色光，下列说法正确的是（）A．在冰晶中，b光的传播速度较大B．从同种玻璃中射入空气发生全反射时，a光的临界角较大C．通过同一装置发生双缝干涉，a光的相邻条纹间距较小D．用同一装置做单缝衍射实验，b光的中央亮条纹更宽3．如图所示，一细束白光经过玻璃三棱镜折射后分为各种单色光，取其中a、b、c三种色光，下列说法正确的是（）A．a、b、c三色光在玻璃三棱镜中的传播速度依次越来越大B．若b光照射某金属可发生光电效应，则c光照射该金属也一定能发生光电效应C．若分别让a、b、c三色光经过一双缝装置，则a光形成的干涉条纹的间距最大D．若让a、b、c三色光以同一入射角，从同一介质射入空气中，b光恰能发生全反射，则c光也一定能发生全反射4．关于下列现象说法正确的是（）A．晨光照射下的露珠显得特别“明亮”是由于光的折射B．火车进站鸣笛时，车站中的乘客听到的频率小于火车鸣笛发出的频率C．电视台发射信号要使用频率较高的电磁波是因为高频电磁波在真空中传播速度更快D．光纤通信及医用纤维式内窥镜都利用了光的全反射原理5．如图所示，光束沿AO方向从空气射向某种介质，折射光线沿OB方向。

下列说法正确的是（）A．这束光从空气进入介质后速度会增大B．这束光从空气进入介质后频率会减小C．这束光从空气进入介质后波长会减小D．若这束光沿BO方向从介质射向空气，可能会发生全反射现象6．物理来源于生活又服务于生活，下列生活和科技现象中涉及到不同的物理知识，其中说法正确的是（）A．当急救车从我们身边疾驰而过，我们听到的急救车鸣笛的音调会先高变低B．刮胡须的刀片的影子边缘模糊不清是光的干涉现象造成的C．篮球运动员伸出双手迎接传来的篮球，然后两手随球迅速收缩至胸前，这样做可以减小篮球对手的冲量D．在水中的潜水员斜向上看岸边物体时，根据光的折射定律得出，看到的物体的像将比物体所处的实际位置低7．如图所示，某透明液体深1 m，一束与水平面成30°角的光线从空气射向该液体，进入该液体的光线与水平面的夹角为45°。

专题十二光学熟练利用反射定律、折射定律及光路可逆作光路图．加深对折射率、全反射、临界角概念的理解．并能结合实际，解决问题．同时应注意对物理规律的理解和对物理现象、物理情景和数学几何知识结合的分析能力的培养．物理光学部分应遵循历史发展线索，理解干涉、衍射、偏振等现象，并能解释生活中的相关物理现象．光的偏振、激光这些内容，与生产、生活、现代科技联系密切，应学以致用．知识点一、几何光学的常见现象决定式:n＝临界角：sin C＝知识点二、光的干涉、衍射和偏振现象出现明暗条纹的条件:路程差Δs＝nλ,明条纹;Δs＝(n＋)λ,暗条纹相邻条纹间距:Δx＝λ应用:(1)光干涉法检查平面的平整度(2)在光学镜头上涂增透膜d＝λ【特别提醒】(1)光的干涉和衍射现象说明光具有波动性,光的偏振现象说明光是横波.(2)光的干涉条纹和光的衍射条纹的最大区别是研究条纹间距是否均匀,中央条纹和两侧条纹的亮度是否相同.知识点三、光电效应及光的波粒二象性物质波的波长λ＝高频考点一、光的折射、全反射例1．（2019·天津卷）某小组做测定玻璃的折射率实验，所用器材有：玻璃砖，大头针，刻度尺，圆规，笔，白纸。

①下列哪些措施能够提高实验准确程度______。

A．选用两光学表面间距大的玻璃砖B．选用两光学表面平行的玻璃砖C．选用粗的大头针完成实验D．插在玻璃砖同侧的两枚大头针间的距离尽量大些②该小组用同一套器材完成了四次实验，记录的玻璃砖界线和四个大头针扎下的孔洞如下图所示，其中实验操作正确的是______。

③该小组选取了操作正确的实验记录，在白纸上画出光线的径迹，以入射点O为圆心作圆，与入射光线、折射光线分别交于A、B点，再过A、B点作法线NN'的垂线，垂足分别为C、D点，如图所示，则玻璃的折射率n=______。

（用图中线段的字母表示）【答案】①AD ②D ③AC BD【解析】①采用插针法测定光的折射率的时候，应选定光学表面间距大一些的玻璃砖，这样光路图会更加清晰，减小误差，同时两枚大头针的距离尽量大一些，保证光线的直线度，因此AD正确，光学表面是否平行不影响该实验的准确度，因此B错误，应选用细一点的大头针因此C错误。

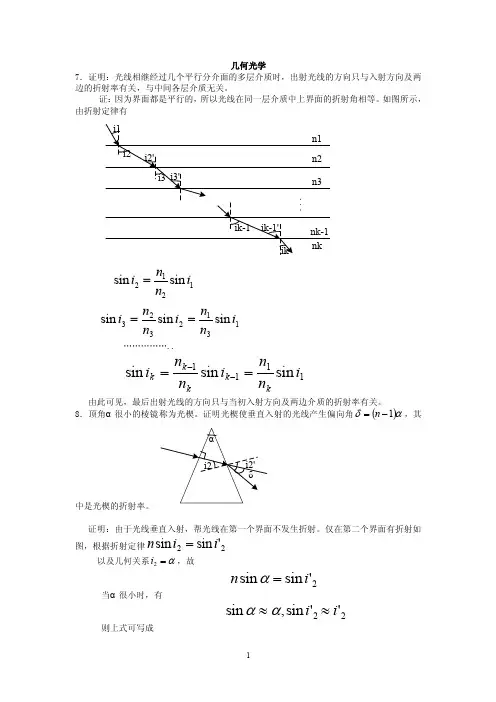
几何光学7．证明：光线相继经过几个平行分介面的多层介质时，出射光线的方向只与入射方向及两边的折射率有关，与中间各层介质无关。

证：因为界面都是平行的，所以光线在同一层介质中上界面的折射角相等。

如图所示，由折射定律有1212sin sin i n n i = 1312323sin sin sin i n n i n n i ==……………..1111sin sin sin i n n i n n i kk k k k ==--由此可见，最后出射光线的方向只与当初入射方向及两边介质的折射率有关。

8．顶角α很小的棱镜称为光楔。

证明光楔使垂直入射的光线产生偏向角()αδ1-=n ，其中是光楔的折射率。

证明：由于光线垂直入射，帮光线在第一个界面不发生折射。

仅在第二个界面有折射如图，根据折射定律22'sin sin i i n =以及几何关系α=2i ，故 2'sin sin i n =α当α很小时，有22''sin ,sin i i ≈≈αα则上式可写成2'i n =α所以偏向角为()αααδ1'22-=-=-=n n i i这个近似公式，在干涉、衍射、偏振中经常要用到。

9.如图1所示，两个顶角分别为0160=ϕ和0230=ϕ的棱镜胶合在一起（090=∠BCD ）。

折射率有下式给出： 2111λb a n += 2222λb a n +=其中 1.11=a 25110nm b = 3.12=a 242105nm b ⨯=(1)确定使得从任何方向入射的光线在经过AC 面时不发生折射的波长0λ，并求出此情形下的折射率n 1和n 2（2）画出入射角相同的波长为红λ、0λ和蓝λ的三种不同光线的路径； （3）确定组合棱镜的最小偏向角（对于满足（1）中条件的波长）；（4）计算平行于DC 入射且在离开组合棱镜时仍平行于DC 的光线的波长。

φ1φ2n1n2A BDC图1图2λ0解：（1）如果满足)()(0201λλn n = ，则波长为0λ的光线从任何方向入射在AC 面上将不发生折射，所以0λ满足关系式：222211λλb a b a +=+解得 nm a a b b 50021120=--=λ在此情形下折射率为 5.1)()(0201==λλn n（2）对波长比0λ长的红光，n 1和n 2均小于1.5。

高考物理专题光学知识点之几何光学经典测试题含答案解析一、选择题1．有关光的应用，下列说法不正确的是（ ）A ．拍摄玻璃橱窗内的物品时，往往在镜头前加一个偏振片以增加透射光的强度B ．光学镜头上的增透膜是利用光的干涉现象C ．用三棱镜观察白光看到的彩色图样是光的折射形成的色散现象D ．在光导纤维束内传送图象是利用光的全反射原理2．下列现象中属于光的衍射现象的是A ．光在光导纤维中传播B ．马路积水油膜上呈现彩色图样C ．雨后天空彩虹的形成D ．泊松亮斑的形成3．半径为R 的玻璃半圆柱体，截面如图所示，圆心为O ，两束平行单色光沿截面射向圆柱面，方向与底面垂直，∠AOB ＝60°，若玻璃对此单色光的折射率n ＝3，则两条光线经柱面和底面折射后的交点与O 点的距离为（ ）A ．3RB ．2RC ． 2RD ．R4．如图所示，一细束平行光经玻璃三棱镜折射后分解为互相分离的a 、b 、c 三束单色光。

比较a 、b 、c 三束光，可知()A ．当它们在真空中传播时，a 光的速度最大B ．当它们在玻璃中传播时，c 光的速度最大C ．若它们都从玻璃射向空气，c 光发生全反射的临界角最大D ．若它们都能使某种金属产生光电效应，c 光照射出的光电子最大初动能最大5．甲、乙两单色光分别通过同一双缝干涉装置得到各自的干涉图样，相邻两个亮条纹的中心距离分别记为Δx 1和Δx 2，已知Δx 1＞Δx 2。

另将两单色光在真空中的波长分别用λ1、λ2，在同种均匀介质中传播的速度分别用v 1、v 2，光子能量分别用E 1、E 2、在同种介质中的折射率分别用n 1、n 2表示。

则下列关系正确的是A ．λ1<λ2B ．v 1<v 2C ．E 1<E 2D ．n 1>n 26．频率不同的两束单色光1和2以相同的入射角从同一点射入一厚玻璃板后，其光路如图所示，下列说法正确的是( )A．单色光1的波长小于单色光2的波长B．在玻璃中单色光1的传播速度大于单色光2的传播速度C．单色光1通过玻璃板所需的时间小于单色光2通过玻璃板所需的时间D．单色光1从玻璃到空气的全反射临界角小于单色光2从玻璃到空气的全反射临界角7．有一束波长为6×10－7m的单色光从空气射入某种透明介质，入射角为45°，折射角为30°，则A．介质的折射率是2B．这束光在介质中传播的速度是1.5×108m／sC．这束光的频率是5×1014HzD．这束光发生全反射的临界角是30°8．如图所示，一束平行光经玻璃三棱镜折射后分解为互相分离的a、b、c三束单色光．比较a、b、c三束光，可知A．当它们在真空中传播时，c光的波长最大B．当它们在玻璃中传播时，c光的速度最大C．若它们都从玻璃射向空气，c光发生全反射的临界角最小D．对同一双缝干涉装置，a光干涉条纹之间的距离最小9．明代学者方以智在《阳燧倒影》中记载：“凡宝石面凸，则光成一条，有数棱则必有一面五色”，表明白光通过多棱晶体折射会发生色散现象．如图所示，一束复色光通过三棱镜后分解成两束单色光a、b，下列说法正确的是A．若增大入射角i，则b光最先消失B．在该三棱镜中a光波速小于b光C．若a、b光通过同一双缝干涉装置，则屏上a光的条纹间距比b光宽D．若a、b光分别照射同一光电管都能发生光电效应，则a光的遏止电压高10．下列说法正确的是（）A．由红光和绿光组成的一细光束从水中射向空中，在不断增大入射角水面上首先消失的是绿光B．光的双缝干涉实验中，在光屏上的某一位置会时而出现亮条纹，时而出现暗条纹C．红光的光子能量比紫光光子能量大D．只有横波才能产生干涉现象11．在杨氏干涉实验中,从两个狭缝到达像屏上的某点的光走过的路程相等,该点即为中央亮条纹的位置(即k=0对应的那条亮条纹),双缝屏上有上下两狭缝,设想在双缝屏后用一块极薄的玻璃片遮盖上方的缝,则屏上中央亮条纹的位置将( ）A．向上移动 B．向下移动C．不动 D．可能向上移动，也可能向下移动12．华裔科学家高锟获得2009年诺贝尔物理奖，他被誉为“光纤通讯之父”．光纤通讯中信号传播的主要载体是光导纤维，它的结构如图所示，其内芯和外套材料不同，光在内芯中传播．下列关于光导纤维的说法中正确的是A．内芯的折射率比外套的小，光传播时在内芯与外套的界面上发生全反射B．内芯的折射率比外套的大，光传播时在内芯与外套的界面上发生全反射C．波长越短的光在光纤中传播的速度越大D．频率越大的光在光纤中传播的速度越大13．如图所示，放在暗室中的口径较大不透明的薄壁圆柱形浅玻璃缸充满水，缸底中心有一红色发光小球（可看作点光源），从上往下看，则观察到（）A．水面有一个亮点B．充满水面的圆形亮斑C．发光小球在水面上的像D．比小球浅的发光小球的像14．如图所示为一块透明光学材料的剖面图，在其上建立直角坐标系xOy，设该光学材料的折射率沿y轴正方向均匀减小，现有一束单色光a从原点O以某一入射角 由空气射入该材料内部，则单色光a在该材料内部可能的传播途径是（）A．B．C．D．15．如图所示，一束红光从空气穿过平行玻璃砖，下列说法正确的是A．红光进入玻璃砖前后的波长不会发生变化B．红光进入玻璃砖前后的速度不会发生变化C．若紫光与红光以相同入射角入射，则紫光不能穿过玻璃砖D．若紫光与红光以相同入射角入射，在玻璃砖中紫光的折射角比红光的折射角小16．某种介质对空气的折射率是2，一束光从该介质射向空气，入射角是 60°，则下列光路图中正确的是（图中 I 为空气，Ⅱ为介质）（）A．B．C．D．17．如图所示，ABC为等腰棱镜，a、b两束不同频率的单色光垂直AB边射入棱镜，两束光在AB面上的入射点到OC的距离相等，两束光折射后相交于图中的P点，以下判断正确的是()A ．在真空中，a 光光速大于b 光光速B ．在真空中，a 光波长大于b 光波长C ．a 光通过棱镜的时间大于b 光通过棱镜的时间D ．a 、b 两束光从同一介质射入真空过程中，a 光发生全反射的临界角大于b 光发生全反射的临界角18．与通常观察到的月全食不同,小虎同学在2012年12月10日晚观看月全食时,看到整个月亮是暗红的．小虎画了月全食的示意图,并提出了如下猜想,其中最为合理的是A ．地球上有人用红色激光照射月球B ．太阳照射到地球的红光反射到月球C ．太阳光中的红光经地球大气层折射到月球D ．太阳光中的红光在月球表面形成干涉条纹19．某单色光由玻璃射向空气，发生全反射的临界角为θ， c 为真空中光速，则该单色光在玻璃中的传播速度是 （ ）A ．B ．C ．cos c θD ．sin c θ20．如图所示，两束单色光a 、b 从水下射向A 点后，光线经折射合成一束光c ，则下列说法中正确的是A ．水对单色光a 的折射率比对单色光b 的折射率大B ．在水中a 光的临界角比b 光的临界角大C ．在水中a 光的速度比b 光的速度小D ．用同一双缝干涉实验装置分别以a 、b 光做实验，a 光的干涉条纹间距小于b 光的干涉条纹间距21．为了表演“隐形的大头针”节目，某同学在半径为r 的圆形软木片中心垂直插入一枚大头针，并将其放入盛有水的碗中，如右图所示．已知水的折射率为43，为了保证表演成功(在水面上看不到大头针)，大头针末端离水面的最大距离h为A．73r B．43r C．34r D．377r22．用a．b．c．d表示4种单色光，若①a．b从同种玻璃射向空气，a的临界角小于b的临界角；②用b．c和d在相同条件下分别做双缝干涉实验，c的条纹间距最大；③用b．d 照射某金属表面，只有b能使其发射电子．则可推断a．b．c．d分别可能是( ) A．紫光．蓝光．红光．橙光B．蓝光．紫光．红光．橙光C．紫光．蓝光．橙光．红光D．紫光．橙光．红光．蓝光23．如图所示，一束光经玻璃三棱镜折射后分为两束单色光a、b，波长分别为λa、λb，该玻璃对单色光a、b的折射率分别为n a、n b，.则()A．λa<λb，n a>n b B．λa>λb，n a<n bC．λa<λb，n a <n b D．λa>λb，n a >n b24．下面事实与光的干涉有关的是（）A．用光导纤维传输信号B．水面上的油膜呈现彩色C．水中的气泡显得格外明亮D．一束白光通过三棱镜形成彩色光带25．如图所示半圆形玻璃砖，圆心为 O，半径为 R．某单色光由空气从 OB 边界的中点 A 垂直射入玻璃砖，并在圆弧边界 P 点发生折射，该折射光线的反向延长线刚好过B点．则（）A．该玻璃对此单色光的折射率为1.5B．光从 A 传到 P 的时间为（c为空气中的光速）C．该玻璃对此单色光的临界角为45°D．玻璃的临界角随入射光线位置变化而变化【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【解析】【详解】A.拍摄玻璃橱窗内的物品时，在镜头前加一个偏振片减弱反射光的强度，故A错误；B.增透膜是利用薄膜干涉，故B正确；C.用三棱镜观察白光，由于三棱镜对不同色光的折射率不同，进出三棱镜的偏折角度不同，出现了不同色光的色散，故C正确；D.光导纤维束内传送图象是利用光的全反射原理，故D正确。