大学物理几何光学习题+公式

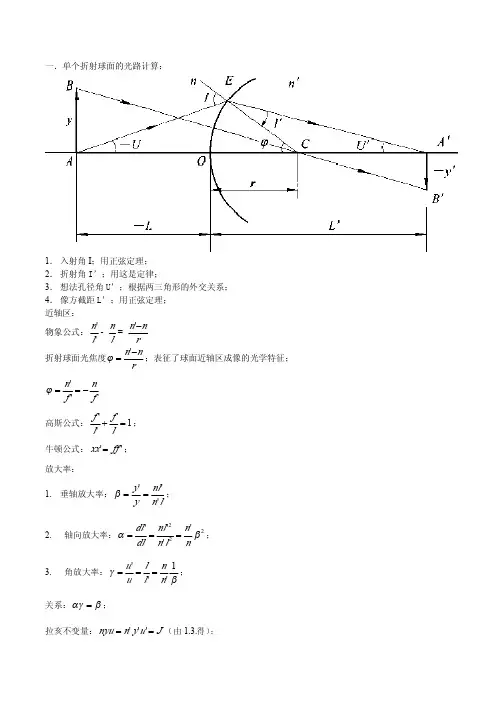
一．单个折射球面的光路计算：1．入射角I ；用正弦定理；2．折射角I’；用这是定律；3．想法孔径角U’；根据两三角形的外交关系；4．像方截距L’；用正弦定理；近轴区：物象公式：-=''l n l n rn n −'折射球面光焦度；表征了球面近轴区成像的光学特征；r n n −='ϕfn f n −==''ϕ高斯公式：；1''=+l f l f 牛顿公式：；''ff xx =放大率：1.垂轴放大率：；ln nl y y '''==β2.轴向放大率：；222''''βαnn l n nl dl dl ===3.角放大率：；βγ1'''n n l l u u ===关系：；βαγ=拉亥不变量：（由1.3.得）；J u y n nyu =='''二．球面反射镜成像焦点和焦距：；；r n 2−=ϕ2'r f f ==n n −='以此带入上面公式得：1.物象公式rl l 21'1=+2．高斯：'11'1f l l =+3．放大率：；；l l '−=β22'βα−=−=l l βγ1'−==l l 三．薄透镜成像1.物象公式：'11'1f l l =−2.放大率：；；l l '=β22'l l =α'l l =γ四．折射平行平板的成像)'11('n d l −=∆五．理想光学系统成像公式1.牛顿公式：''ff xx =2.高斯公式：1''=+lf l f 3.焦距关系：nn f f ''−=4.光焦度：f n f n −==''ϕ5.拉亥不变量：'tan ''tan u y n u ny =6.放大率：；ln nl f x x f y y '''''=−=−==β；222''''βαnn l n nl x x ==−=；βγ''''tan 'tan n n x f f x l l u u =====六．理想光学系统的组合（双光）21'f f d −∆+=1.焦点位置：；∆−=''22f f x F ∆='11f f x F 2.焦距公式：∆=21f f f 3.主点公式：；''2f d l H ∆=1f d l H ∆=4.光焦度公式：22121n d ϕϕϕϕϕ−+=无焦系统（近出都是平行光）1.物象关系：'''221112f f x f f x =2.垂轴放大率：'12f f =β3.轴向放大率：''1122f f f f =α4.角放大率：'21f f =γ厚透镜基点一般公式：；；；111−−=n r f 1'11−=n nr f 122−=n nr f 1'22−−=n r f 光学间隔1)1()('1221−−+−=+−=∆n d n r r n f f d f d n r r n n r nr f f f −=−+−−=∆−=])1()()[1('''122121；d n r r n dr l H )1()('122−+−−=d n r r n dr l H )1()(121−+−−=七．景深；11||'z z β=22||'z z β=远景近景位置：；01Z D Dp p −=2Z D Dp p +=远景近景深度：；001Z D pZ −−=∆002Z D pZ +−=∆景深：2020212Z D DpZ −−=∆+∆=∆Microsoft 公式3.0。

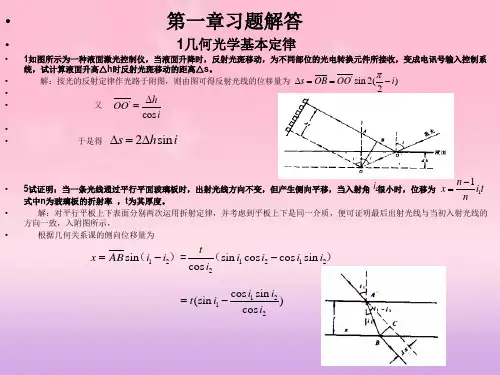
几何光学基本原理习题答案几何光学是光学中的一个重要分支，研究光的传播和反射的规律。

它是光学理论的基础，也是应用最广泛的光学学科之一。

在学习几何光学的过程中，我们常常会遇到一些习题，下面我将为大家提供一些几何光学基本原理习题的答案。

1. 问题：一束光从空气射入玻璃介质，入射角为30°，折射角为20°，求玻璃的折射率。

解答：根据折射定律，光线从空气射入玻璃介质时，入射角、折射角和两种介质的折射率之间满足关系：n1*sinθ1 = n2*sinθ2。

其中，n1为空气的折射率，一般取为1；θ1为入射角，θ2为折射角，n2为玻璃的折射率。

代入已知条件，得到：1*sin30° = n2*sin20°。

解方程可得：n2 ≈ 1.5。

所以，玻璃的折射率约为1.5。

2. 问题：一束光从玻璃射入空气，入射角为60°，折射角为45°，求玻璃的折射率。

解答：同样根据折射定律，光线从玻璃射入空气时，入射角、折射角和两种介质的折射率之间满足关系：n1*sinθ1 = n2*sinθ2。

其中，n1为玻璃的折射率，θ1为入射角，θ2为折射角，n2为空气的折射率，一般取为1。

代入已知条件，得到：n1*sin60° = 1*sin45°。

解方程可得：n1 ≈ 1.15。

所以，玻璃的折射率约为1.15。

3. 问题：一束光从玻璃射入水，入射角为45°，折射角为30°，求水的折射率。

解答：同样根据折射定律，光线从玻璃射入水时，入射角、折射角和两种介质的折射率之间满足关系：n1*sinθ1 = n2*sinθ2。

其中，n1为玻璃的折射率，θ1为入射角，θ2为折射角，n2为水的折射率。

代入已知条件，得到：n1*sin45° = n2*sin30°。

解方程可得：n2 ≈ 1.33。

所以，水的折射率约为1.33。

4. 问题：一束光从空气射入玻璃，入射角为60°，折射角为90°，求玻璃的折射率。

物理光学公式物理光学公式引言•光学是研究光的传播和性质的学科，其中物理光学是光学中的一个重要分支。

•物理光学公式是研究光的传播和反射折射等现象时使用的数学表达式。

光的速度公式•由于光在真空中的传播速度接近于恒定值，因此可以使用以下公式来计算光的速度：–光速公式：c = νλ•其中c表示光速，ν表示光的频率，λ表示光的波长。

光的折射公式•光在从一介质传播到另一介质时，会发生折射现象，折射现象可以用以下公式来描述：–折射公式：n₁sinθ₁ = n₂sinθ₂•其中n₁和n₂分别表示两个介质的折射率，θ₁和θ₂分别表示光的入射角和折射角。

光的反射公式•光在与介质界面发生反射时，可以使用以下公式来计算反射角度：–反射公式：θᵣ = θᵢ•其中θᵣ表示反射角度，θᵢ表示入射角度。

光的干涉公式•光的干涉是指两束或多束相干光叠加后产生的干涉现象，可以使用以下公式计算干涉条纹的位置：–干涉公式：d⋅sinθ = mλ•其中d表示两束光的光程差，θ表示干涉条纹的角度，m表示干涉级次，λ表示光的波长。

光的衍射公式•光的衍射是指光通过孔径或物体边缘时发生的弯曲和扩散现象，可以使用以下公式计算衍射条纹的位置：–衍射公式：a⋅sinθ = mλ•其中a表示孔径或物体的尺寸，θ表示衍射条纹的角度，m表示衍射级次，λ表示光的波长。

结论•物理光学公式能够帮助我们理解光的传播和性质。

•研究和应用这些公式可以解决光学中的各种问题，并推动光学技术的发展。

以上就是一些常见的物理光学公式，它们在实际应用中扮演着重要的角色。

通过学习和理解这些公式，我们能够更好地理解光的行为，并在光学领域取得更多的成果。

光的衍射公式的应用•光的衍射公式在实际应用中有许多重要的应用，下面我们来介绍一些常见的应用场景。

衍射光栅•光栅是一种光学元件，它由许多平行的透明或不透明线条组成，可以用于光的衍射。

•根据衍射公式，我们可以计算出衍射光栅的条纹位置和间距，从而实现光的分光和波长测量。

物理选修光学公式
光学公式是物理学中的重要内容，它描述了光的传播和反射等现象。

在光学选修课中，我们学习了许多光学公式，下面就让我们来一一了解。

1. 折射定律
折射定律是光学中最基本的公式之一，它描述了光线在两种介质之间传播时的偏折现象。

折射定律的表达式为：n1sinθ1=n2sinθ2，其中n1和n2分别为两种介质的折射率，θ1和θ2分别为入射角和折射角。

2. 薄透镜公式
薄透镜公式是描述光线通过薄透镜成像的公式，它可以计算出物距、像距和焦距之间的关系。

薄透镜公式的表达式为：1/f=1/v-1/u，其中f为透镜的焦距，v为像距，u为物距。

3. 光的干涉公式
光的干涉是光学中的重要现象之一，它可以用来解释许多光学现象，如干涉条纹、薄膜干涉等。

光的干涉公式为：δ=(2π/λ)(d1-d2)，其中δ为相位差，λ为光的波长，d1和d2分别为两条光线到达某一点的路程差。

4. 光的衍射公式
光的衍射是光学中的另一个重要现象，它可以用来解释许多光学现象，如单缝衍射、双缝干涉等。

光的衍射公式为：sinθ=mλ/d，其中θ为衍射角，m为衍射级数，λ为光的波长，d为衍射孔径的大小。

5. 光的偏振公式
光的偏振是光学中的另一个重要现象，它可以用来解释许多光学现象，如偏振片、波片等。

光的偏振公式为：E=E0sin(ωt-kx)，其中E为电场强度，E0为电场强度的最大值，ω为角频率，t为时间，k 为波矢量，x为位置。

以上就是光学选修课中常见的几个公式，它们描述了光的传播、反射、折射、干涉、衍射和偏振等现象。

在学习光学时，我们需要掌握这些公式，并能够灵活运用它们解决实际问题。

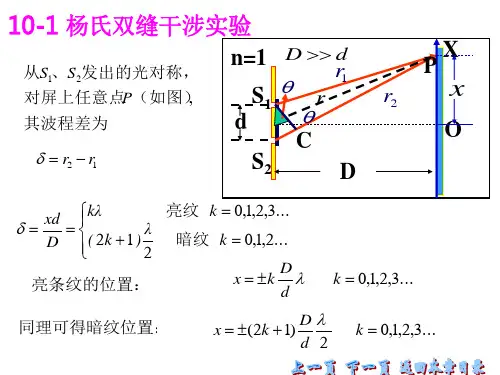
大学物理光学部分有关于明暗的公式及其结论 1．获得相干光的方法 杨氏实验.......,2,1022，，=⋅±==k k D xd λδ 此时P 点的光强极大，会出现明条纹。

......,2,102)12(，，=⋅+±==k k D xd λδ此时的光强极小，会出现暗条纹。

或者，dD kx 22λ±= 此时出现明条纹 d D k x 2)12(λ+±= 此时出现暗条纹。

屏上相邻明条纹或者暗条纹的间距为：dD x λ=∆。

洛埃镜。

半波损失。

2．薄膜等厚干涉。

○1根据光程差的定义有： ○2劈尖干涉：暗条纹。

明条纹。

,...2,1,0,2)12(22,...2,1,2222=⋅+=+==⋅=+=k k d k k d λλδλλδ 相邻明条纹或者暗条纹对应的空气层厚度差都等于2λ 即：21λ=-+k k d d 。

则设劈尖的夹角为θ，相邻明纹或者暗纹的间距 a 应满足关系式：2sin λθ=a○3牛顿环： 直接根据实验结果的出结论为：⎪⎭⎪⎬⎫===⋅-=暗条纹明条纹,...3,2,1,0,R ,...3,2,1,2)12(k k r k R k r λλ 3.单缝的夫琅禾费衍射关键词：半波带。

注意：半波带的数目可以是整数也可以是非整数。

结论：光源是平行光的单缝夫琅禾费衍射的条纹明暗条件为：明条纹，）（暗条纹,...3,2,10,212sin ,...3,2,1,22sin =⋅+±==⋅±=k k a k k a λϕλϕ 特殊地当ϕ=0时，有：当将单缝换做圆孔时，得到中心的明亮光斑为艾里斑，且其半角宽度0ϕ为： D λϕϕ22.1sin 00=≈ 这一角度也是我们在天文望远镜中的最小分辨角。

4.衍射光栅及光栅光谱。

关键词：光栅方程，主极大条纹，谱线的缺级，暗纹条件。

光栅方程：.,.....2,1,0,sin )(明条纹=±=+k k b a λϕ主极大条纹：满足光栅方程的明条纹，也称作光谱线。

高考光学部分公式总结第一篇：高考光学部分公式总结高考光学部分公式总结（一）几何光学1、概念：光源、光线、光束、光速、实像、虚像、本影、半影。

2、规律：（1）光的直线传播规律：光在同一均匀介质中是沿直线传播的。

（2）光的独立传播规律：光在传播时，虽屡屡相交，但互不干扰，保持各自的规律传播。

（3）光在两种介质交界面上的传播规律①光的反射定律：反射光线、入射光线和法线共面；反射光线和入射光线分居法线两侧；反射角等于入射角。

②光的析射定律：a、折射光线、入射光线和法线共面；入射光线和折射光线分别位于法线的两侧；入射角的正弦跟折射角的正弦之比是常数。

即 sini=常数sinrb、介质的折射率n：光由真空（或空气）射入某中介质时，有n=于介质的性质，叫介质的折射率。

c、设光在介质中的速度为 v，则： n=sini，只决定sinrc可见，任何介质的折射率大于1。

vd、两种介质比较，折射率大的叫光密介质，折射率小的叫光疏介质。

③全反射：a、光由光密介质射向光疏介质的交界面时，入射光线全部反射回光密介质中的现象。

b、发生全反射的条件：ⓐ光从光密介质射向光疏介质；ⓑ入射角等于临界角。

临界角C sinC=1 n ④光路可逆原理：光线逆着反射光线或折射光线方向入射，将沿着原来的入射光线方向反射或折射。

归纳: 折射率n=λ真sinic1===≥1 sinrvsinCλ介5、常见的光学器件：（1）平面镜（2）棱镜（3）平行透明板（二）光的本性人类对光的本性的认识发展过程（1）微粒说（牛顿）（2）波动说（惠更斯）①光的干涉双缝干涉条纹宽度∆x=Lλ(波长越长，条纹间隔越大)d应用：薄膜干涉——由薄膜前后表面反射的两列光波叠加而成，劈形薄膜干涉可产生平行相间干涉条纹，检查平面，测量厚度，光学镜头上的镀膜。

②光的衍射——单缝（或圆孔）衍射。

泊松亮斑第二篇：最新高考物理公式总结归纳整理高考物理公式大全1.胡克定律：F=Kx(x为伸长量或压缩量,K为倔强系数，只与弹簧的原长、粗细和材料有关)2.重力：G=mg(g随高度、纬度、地质结构而变化)3、求F、的合力的公式：αF2FF1θＦ＝合力的方向与F1成a角：tga=注意：(1)力的合成和分解都均遵从平行四边行法则。

光学物理公式
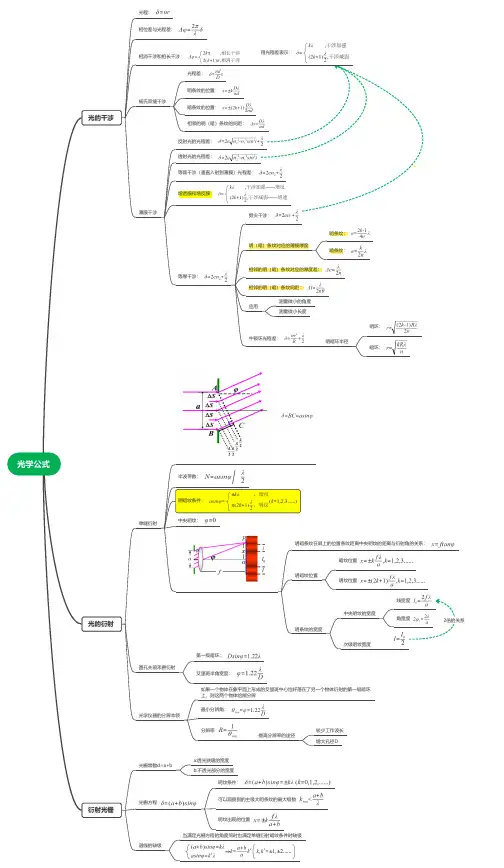
大学物理光学公式波动光学杨氏双缝干涉x=kDλ/d，薄膜干涉2ne + λ/2 =kλ(亮纹)单缝衍射a sinΨ=kλ(暗纹)asinΨ=(2k+1)λ／2 亮纹光栅方程(a+b)sinΨ=kλ。

1，透镜的等光程性，使用透镜不会产生附加光程差，半波损失，入射光从光疏（n1小）掠射（入射角约90°) 或正射(入射角约0°) 到光密媒质（n2 大)的界面时，产生半波损失。

光密→光疏无半波损失。

折射无半波损失。

2，条纹特点单色光照射：一系列平行的明暗相间的条纹；θ不太大时条纹等间距，中间级次低；Δx ∝λ。

白光照射：零级明纹为白色，其它亮纹构成彩带，由紫到红，第二级开始重合。

3，牛顿第一定律：任何物体都保持静止或匀速直线运动状态，除非它受到作用力而被迫改变这种状态。

牛顿第二定律：物体受到外力作用时，所获得的加速度a的大小与外力F的大小成正比，与物体的质量m成反比；加速度的方向与外力的方向相同。

1.37 F=ma牛顿第三定律：若物体A以力F作用与物体B，则同时物体B必以力F2作用与物体A;这两个力的大小相等、方向相反，而且沿同一直线。

 光学•几何光学基本公式  z折射定律    折射光线在入射面内，且 n1 sin i1 = n2 sin i2  n : 介质的折射率  c n=   u   c : 真空光速  u : 介质中的光速    全反射 如果 n1 > n2 ，则当 i1 > ic 时发生全反射。

 ic = arcsinn2 为临界角。

  n1z  成像公式    „ 球面反射镜       u  1+1 1 = v f焦距： f =      横向放大倍数 M≡ y′ v =−   y ur   2 凹面镜： r > 0   凸面镜： r < 0    „单球面透镜透镜透镜     n1 n2 n1 − n2  u+v=−R  M =−         n1 v ⋅   n2 u凸面迎光    R>0  凹面迎光    R < 0 „薄透镜   1 1 1 + =   u v fv M =−   u   焦距公式： ⎛1 1 ⎞ 1 = (n − 1) ⎜ − ⎟   f ⎝ R1 R2 ⎠如像与物都在折射率为 n1 的介质中，则 n ⎛ 1 1 1 ⎞ = ( n′ − 1) ⎜ − ⎟ ， n′ =   n1 f ⎝ R1 R2 ⎠„   理想几何光学成像系统  物方任一点发出的所有经过成像系统的光线都汇聚于像方一点。