C
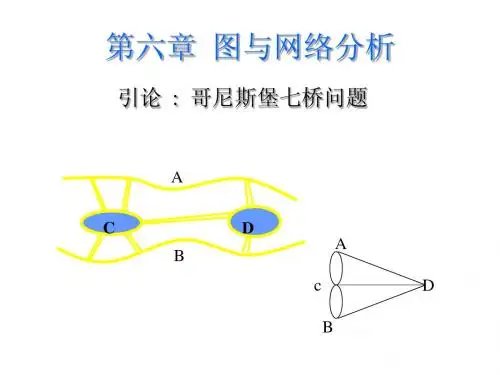
哥尼斯堡七桥问题变为,能否从图 的某一点开始不重复地一笔画出 这个图形.你能一笔画出吗?
B 欧拉在论文中证明了这是不可 能的.为什么?
A
D
理由是:图上的每一个顶点都与 奇数条边相连接,不可能一笔画 出.
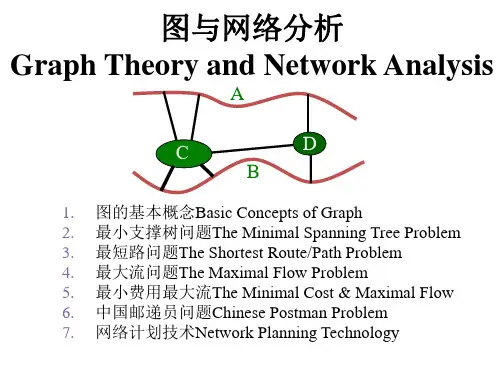
第一节 图的基本概念与基本定理 一.图的基本概念 日常生活中我们见过大量的图,如各种交通图, 各种管网图(电网图,自来水管网,煤气管网,计 算机网络).都是用点表示研究对象,用线(边) 表示这些对象间的关系.因此,图可以定义为点 和边的集合.记作G=[V,E],其中V是点的集合,E 是边的集合.在图的点和边上赋予权值(如距离, 费用,容量等)则称这样的图为网络图记为N,网 络图又可分有向网络图和无向网络图.
B
C
结果:比赛顺序 是A,C,B,F,E,D.
D
A
F
E
练习1 有甲,乙,丙,丁,戊,己六名运动员报名参 加A,B,C,D,E,F六个项目比赛.报名情况如下表, 问六个项目的比赛顺序如何安排,做到每名运 动员不连续参加两项比赛.
A 甲 乙 丙 丁 戊 己 * * * * * * * B C D * * * * * E F *
铁路的转用线,管理机构图,学科分类图,AHP决策方法 等,都可用树来表示.
树的特点:1.树是边数最多的无圈连通图,即在 树上再任意增加一条边,必定出现圈; 2.树的任意两点间,有一条且仅有一 条通路.也可以说,树是最脆弱的连通图,只要 在树中去掉任一条边,图就不连通了.
图的最小部分树(最小生成树):设 G 2 是一个图,如 果 G 1 是 G 2 的支撑子图(部分图),且 G 1 是一个树, 则称 G 1 是 G 2 的部分树.树的各条边称为树枝.在 图的每条边上赋予权值的图称为赋权图. 在 G 2 中一般含有许多部分树,其中树枝总长为 最小的部分树,称为该图的最小部分树.






![#6 运筹学讲义[图与网络]](https://uimg.taocdn.com/9743fc0cbb68a98271fefac3.webp)

