《三角恒等变换》复习课

三角恒等变换复习教案学习目标:(1)了解两角和与差正弦、余弦、正切公式之间的内在联系.培养逻辑推理能力.(2)掌握两角和与差的正弦公式、正切公式,并会运用它们进行有关计算、化简、证明.(3)通过实例熟悉一些解题的技巧并增强利用公式解决具体问题的灵活性. 重点:熟练、灵活的应用三角公式.难点:变换中的技巧.复习与巩固两角和与差的正弦、余弦、正切公式的内在联系：三角函数恒等变形实质是对角、函数名称的变化，而转化的依据就是一系列三角公式，如:①同角三角函数关系——可实现函数名称的转化；②诱导公式及和、差角的三角函数——可实现角的形式的转化.在应用公式时要注意它的逆向变换、多向变换，即对公式要“三会”:正用、逆用、变用.要注意通过拆角、拼角的技巧用已知角表示未知角.一、关于和角与差三角公式特别注意公式的结构,用活公式. :sin()sin cos cos sin ;sin()sin cos cos sin ,,:2sin cos sin()sin();2cos sin sin()sin().αβαβαβαβαβαβαβαβαβαβαβαβ+=+-=-=++-=+--如在公式中应用方程的思想得 :2cos cos cos()cos();2sin sin cos()cos()C C αβαβαβαβαβαβαβαβ+-=++--=+--同理由公式可得tan tan :tan(),:1tan tan tan tan tan()(1tan tan ),tan tan ,tan tan ,.αβαβαβαβαβαβαβαβ++=-+=+-+又如公式可以变形为特别是公式中有式子因此常又与一元二次方程联系在一起 二、习题复习与巩固231.sin ,,cos ,,tan().34αβαβαβ==-++例已知且是第二象角求的值()()S C αβαβ++()()S C αβαβ--ββ-以代ββ-以代tan(60)tan(30)2..1tan(60)tan(30)αααα+-+++⋅+ 例计算的值 1113.sin ,cos(),,(0,),7142πααβαββ=+=-∈例已知且求的值 31234.,cos(),sin(),sin 2,sin 224135ππβααβαβαβ<<<-=+=-例已知求的值 42sin 3cos (1)55.(1)sin().32cos 3sin (2)547(2)8sin 5cos 6,sin(),808cos 5sin .αβαβαβαβαβαβ⎧+=⎪⎪+⎨⎪+=⎪⎩+=+=+例已知求的值求的值6(1):3cos 3sin ;(2):;(3):sin .1212x x x x ππ-+例化简化简求值7.:tan15tan30tan15tan30++ 例计算():1.[0,];22.;3.;4.π请同学们把下列内容记一记或默一默间的特殊角的三角函数值同角三角函数基本关系式九组诱导公式两角和与差的三角函数公式三、综合训练题 28.0(0)tan ,tan ,tan().ax bx c a a c αβαβ++=≠≠+例已知一元二次方程且的两个根为求的值tan tan :tan()1tan tan αβαβαβ++=-分析tan tan .tan tan b a ca αβαβ⎧+=-⎪⎪⎨⎪=⎪⎩而代入即可 21.670tan ,tan ,:sin()cos()x x αβαβαβ++=+=+变式题已知一元二次方程的两个根为求证22.,(tan ,0),(tan ,0)()(23)20(0),tan().m A B f x mx m x m m y αβαβ=+-+-=≠=+变式题设为实数是二次函数图象上的两点求的最小值min 923:00,(,0)(0,],tan tan ,4233tan tan tan(),.24m m m m m y m y m αβαβαβ-∆≥≠∈-∞+=--=∴=+==-∴=- 分析且得 9.:tan tan tan tan tan tan ABC A B C A B C ∆++=⋅⋅例在中,求证:tan()tan .A B C +=-分析利用10.,(0,),:(1tan )(1tan )2:.24A B A B A B ππ∈++=+=例已知求证的充要条件是 :tan tan tan()(1tan tan )2T αβπαβαβαβ++=+-分析利用的变式.:(1tan1)(1tan 2)(1tan3)(1tan 44)++++ 变式题化简11.:[2sin50sin10(1)]+ 例求值:50,10,80,60,90,.分析都不特殊角但其和却是特殊角故可考虑逆用两角和公式求其三角函数值:cos10(2sin 50sin10)80cos102cos(6010)(2sin 50sin10)cos1050cos10cos50sin10)60=+-=++==思路一原式:[2sin 50sin10(1tan 60tan10)]80tan 60tan10)[2sin 50sin10]tan(6010)2cos50(2sin 50sin10)cos10=++-=+-=+==思路二原式2222sin()sin()tan 12.:1.sin cos tan αβαββαβα+-=-例求证 :,,.分析观察左右两边的差异从左向右证明要解决角的差异如果从右向左证明解决名称的差异32sin 13.:tan tan .22cos cos 2x x x x x -=+例求证:,,.,,.分析此题各式间的差异较大不仅角之间的差异而且函数名称及结构之间也存在较大差异为此要重点抓住某一特征差异进行分析以求突破 3sin tantan ;322cos cos 222sin sin .333cos()cos()cos cos 222222x x x x x x x x x x x x x =-=⋅==-++⋅左边右边 114.,0,cos(),22292sin(),tan .232ππβαπβαααββ<<<<-=-+-=例已知求的值 :()(),,22242,,,4222αββαπβαβαππαπαββ+=---<-<+<-<分析而再求出的正弦余弦则问题可解22sin ;cos tan 227227235αβαβαβ+++==∴= 33:,0,cos(),4444535sin(),sin().413ππππαβαπβαβ<<<<-=-=+变式题已知求的值15.,,,,tan tan tan .2222ABC A B C A C A C ∆++例在已知成等差数列求的值:,,223tan()22,tan tan tan 2222A C A C A C A C π+=∴+=++=分析由题意得由公式变形得 2cos10sin 2016.cos 20-例求的值:103020=- 分析17.sin(2)2sin 0,:tan 3tan().αββααβ++==+例已知求证 :2();()αβαβαβαβα+=++=+-分析518.sin(),0,:4134cos 2.cos()4x x x x πππ-=<<+例已知求的值 :2()();().44424cos 22413cos()4x x x x x x x ππππππ=+--+=--==+ 分析 2219.(1)tan 5,sin 5(1tan 5tan 2.5).3tan 15(2).13tan 15a =+--例已知求的值求的值:(1),;(2),分析切化弦再逆用公式因式分解后引入辅助角再逆用公式20.,,,lgsin lgsin lgsin lg 2..A B C ABC A B C ∆--=例已知是的三个内角且试判断此三角形的形状特征 :,:sin sin()A B C =+分析利用在三角形中有。

《三角恒等变换》复习课嘉善高级中学项善芳【教学目标】：1、熟练掌握两角和（差）的正弦、余弦、正切公式，二倍角的正弦、余弦、正切公式，理解它们的内在联系，掌握本章的知识结构；2、能运用上述公式进行简单的恒等变换，使学生进一提高运用联系转化的观点去处理问题的自觉性，感受一般与特殊的思想，换元思想、方程思想在三角恒等变换中的作用；3、通过三角恒等变换，培养学生的推理能力和运算能力，使学生体会三角恒等变换的工具性作用，体验它们在数学中的一些应用。

【教学重点】：运用两角和（差）、二倍角的的正弦、余弦、正切公式进行三角变换，感受数学思想方法在三角变换中的作用，体验三角变换在数学中的应用。

【教学难点】：运用三角变换进行求值、证明、化简的分析思路的感悟。

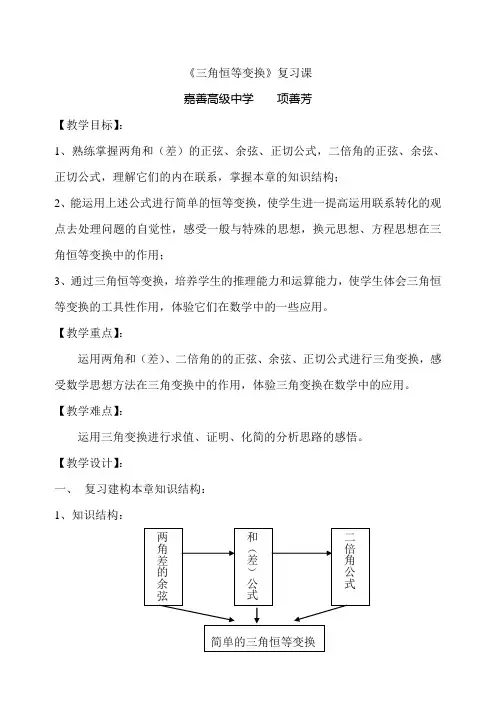
【教学设计】：一、复习建构本章知识结构：1、知识结构：帮助学生从整体上把握本章知识结构，对知识网络进行梳理。

2、公式回顾：帮助学生回顾公式，为具体运用公式做好必要的知识铺垫。

二、 公式在三角函数的求值中的运用：三角函数的求值主要有两种类型：一是给角求值；二是给值求值。

1、 给角求值：利用诱导公式、同角三角函数的基本关系式、两角和差、二倍角公式等，化非特殊角为特殊角，在转化过程中注意公式的正逆用。

例1、计算： 37tan 23tan 337tan 23tan ++练习1、求值： 58cos 77sin 148cos 347sin +2、 给值求值：灵活利用三角恒等变形中的拆角变形及两角和差、倍角公式的综合运用。

例2、已知,222,20,322s i n ,912c o s πβαππβαβαβα<-<-<-<=⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛-求⎪⎭⎫ ⎝⎛+2cos βα的值。

练习2、已知πβπα<<<<20，()53sin ,54sin -=+=βαα，求βsin 的值。

三、 公式在三角函数的化简与证明中的运用：由于三角函数式中包含着各种不同的角和不同的函数种类，以及不同的式子结构，所以在三角函数的化简与证明中，应充分利用所学的三角函数的同角三角函数基本关系式、和差倍角等公式，从角入手，找出待化简或证明的式子中的差异，然后选择适当的公式“化异为同”，实现三角函数的化简与证明。

三角恒等变换复习课一、学习目标1. 通过本节复习要求同学们能记住和差倍半及和差化积、积化和差公式.2. 能熟练运用所记公式解决三角恒等变换的相关问题.3. 通过本节复习体会凑角、換元、化归等数学思想.二、学法指导体会三角恒等变换中角、式、三角函数名称微妙变化给三角恒等变换证明的影响。

三、知识链接复习旧知识：复习知识：：（1）cos()αβ+= （2）()cos αβ-=（3）()sin αβ+= （4）()sin αβ-=（5） ()tan αβ+= （6）()tan αβ-=（7）sin 2α= （8）cos2α= = =(9) tan 2α=_______________________22cos ___________________sin ___________2cos_______tan _______________________22αααα======== sin cos _________.cos sin __________.cos cos _________.sin sin ________.αβαβαβαβ====sin sin _______.sin sin _______.cos cos _______.cos cos _______.θϕθϕθϕθϕ+=-=+=-=()sin cos sin y a x b x A x φ=+=+其中A、cos φ=、sin φ=tan b aφ=. man y =min y =四、自测试题1. 化简:(1).x x + （2）.3cos 2x x(3)()()sin 2sin cos 2sin sin cos αβαβαβαβ+-++44x x ππ⎛⎫⎛⎫-+- ⎪ ⎪⎝⎭⎝⎭(5)sin164sin 224sin 254sin314︒︒︒︒+2.()()tan 3,tan 5.αβαβ+=-= 求tan 2,tan αβ的值.3. 己知函数()sin sin cos 66f x x x x a ππ⎛⎫⎛⎫=++-++ ⎪ ⎪⎝⎭⎝⎭的最大值为 1.(1) 求常数a 的值.五、当堂检测1.(1) 求tan 20tan 4020tan 40︒︒︒︒+的值.(2) 若3,4παβ+=求()()1tan 1tan αβ--的值. (3) 求tan 20tan 40tan120tan 20tan 40︒︒︒︒︒++的值.2. 已知()()13cos ,cos ,55αβαβ+=-= 求tan tan αβ的值.3. 己知函数()44cos 2sin cos sin f x x x x x =--（1）求()f x 的最小正周期;（2）当0,2x π⎡⎤∈⎢⎥⎣⎦时, 求()f x 的最小值以及此时x 的集合.六、知识清单.熟记公式, 学科长检查组员默写.七、日清反思。