下载文档原格式
1.①与a (0°<cr<360°)终边相同的角的集合(角a 与角0的终边重合)：{〃| 0*x36(T+a,展z}② 终边在龙轴上的角的集合：{0|0二Rxl80°,Rwz} ③ 终边在y 轴上的角的集合：0|0*xl8O°+9O°,展z} ④ 终边在坐标轴上的角的集合：{0|0 = £x9O°,/z} ⑤ 终边在尺轴上的角的集合：{01 0 = k x 180° + 45°" Z} ⑥ 终边在y = -x 轴上的角的集合:畅10 = Rx 180° -45°,展z}⑦ 若角a 与角0的终边关于兀轴对称，则角。
与角0的关系：a = 360°k-j3⑧ 若角a 与角0的终边关于y 轴对称，则角a 与角0的关系：^ = 3607 + 180°-0⑨ 若角a 与角0的终边在一条直线上，则角仅与角0的关系：Q = 18O°P + 0⑩角Q 与角0的终边互相垂直，则角a 与角0的关系：a = 36O7 + 0±9O 。
三角函数定义域f(x) = siav {x | xe R} fM = coy {x\xe R}f(x) = tanx彳 x | XG /?且xH k 兀+ — 7t 、kw Z >/(x) = coU{x | xe /?£Lx 丰 k 兀、ke Z}f(x) = secx V x| XG R 且k 兀+ —Z2>f(x) = cscx{x | xe R 且兀工k 兀、k G Z }三角函数的公式:(-)基本关系公式组一 公式组二sint • cscx=l sin xtanv" -------cosx •少2 <sin^v+cos 尸 1sin(23 + x) = sin x cos(2to + x) = cosx cosx • sccx=lcosxcotx=———sin xl+tan 2x=scc 2x tan(2^ + x) = tanx tanv • cotv=ll+cot 2x=csc 2xcot(2^ + x) = cotx(二)角与角之间的互换 公式组一公式组二cos(a + 0) = cos a cos 0 — sin a sin 0 sin 2a = 2 sin a cos a公式组三sin(-x) = - sin x cos(-x) = cos x tan(-x) = - tan x cot(-x) = - cot xSZCOS 三角函数值人小关系图 1、2. 3. 4表示第一、二、三、注意：①y = -sin 兀与y = sin x 的单调性正好相反；) = -cosx 与y = cosx 的单调性也同样相反•一般地,sin(a + 0) = sin a cos 0 + cos a sin 0 sin(a - 0) = sin a cos 0 — cos a sin 0tan 2a =2 tan cr1-tan 2 a .a , 11 - cos a sm — = ± J ---------2 V 2 1 - tan a tan pa , 11 + cos a cos — = ±y ------------------2 V 2z c 、tana-tan Btan(a —0) = --------------- J1 + tan a tan p公式组四sin cos a , 1-cosa sin a 1-coscr tan ——=± J= 2 Vl + cosa 1 + cosa公式组三sincr公式组五P = — [sin (a 4- 0)+sin(a_0)] 2 cos 6T sin p = g[sin("+ 0)_sin (Q-0)] cosacos^ = l[cos( a + 0)+cos(a-0)]sin as\n /3 = --- [cos(a + 0)- cos(a - 0)]・ q c ・ a + 0 a-0sin a + sin p = 2sin ----- - cos ---- —2 2 . a+0 . a-p sin cr-sin p = 2 cos -------- s in -------- 2 2Q 小 Q+# a~COS (7+cos p = 2cos — cos —Y~Q c ・ Q+# ・ a~Pcos a 一 cos 0 = -2 sin ------ s in ------- 2 2sin 15' =cos 75'=卫二返，sin 75° = cos 15、空土丄，tan 15 = cot 75 = 2 - VJ, tan 75 =cotl5° = 2 +VJ.44 c a2 tan —・ 2 sin a = ---------- —1 + tan — (2 a1-tan — cos a = ------------------- — 2 tan — 2 tan a = --------- — ■ 2 Q 1 - tan ~ —2coscos(+龙-G )二 sin 。
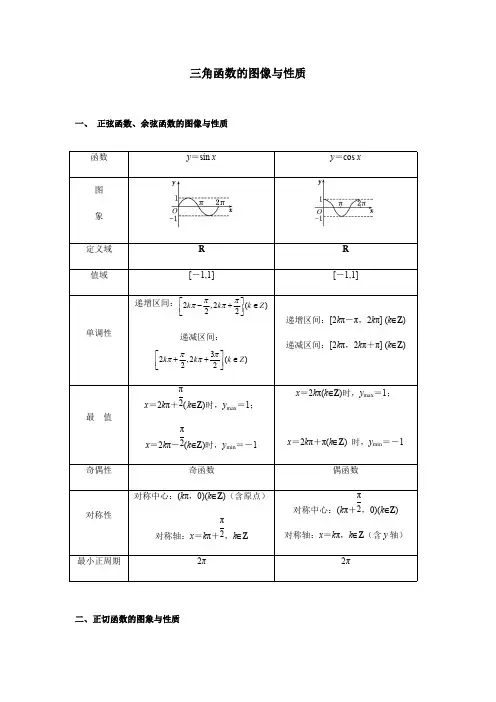
i ng si nt he i rb ei n ga re g三角函数的图像与性质一、 正弦函数、余弦函数的图像与性质二、正切函数的图象与性质函数y ＝sin x y ＝cos x图象定义域RR 值域[－1,1][－1,1]单调性递增区间：2,2()22k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦递减区间：32,2()22k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦递增区间：[2k π－π，2k π] (k ∈Z )递减区间：[2k π，2k π＋π] (k ∈Z )最 值x ＝2k π＋(k ∈Z )时，y max ＝1；π2x ＝2k π－(k ∈Z )时，y min ＝－1π2x ＝2k π(k ∈Z )时，y max ＝1；x ＝2k π＋π(k ∈Z ) 时，y min ＝－1奇偶性奇函数偶函数对称性对称中心：(k π，0)(k ∈Z )（含原点）对称轴：x ＝k π＋，k ∈Zπ2对称中心：(k π＋，0)(k ∈Z )π2对称轴：x ＝k π，k ∈Z （含y 轴）最小正周期2π2π定义域{|,}2x x k k Z ππ≠+∈值域R单调性递增区间(,)()22k k k Z ππππ-+∈奇偶性奇函数对称性对称中心：（含原点）(,0)()2k k Z π∈最小正周期π三、三角函数图像的平移变换和伸缩变换1. 由的图象得到()的图象x y sin =)sin(ϕω+=x A y 0,0A ω>>xy sin =方法一：先平移后伸缩方法二：先伸缩后平移操作向左平移φ个单位横坐标变为原来的倍1ω结果)sin(ϕ+=x y xy ωsin =操作横坐标变为原来的倍1ω向左平移个单位ϕω结果)sin(ϕω+=x y 操作纵坐标变为原来的A 倍结果)sin(ϕω+=x A y 注意：平移变换或伸缩变换都是针对自变量x 而言的，因此在用这样的变换法作图象时一定要注意平移与伸缩的先后顺序，否则会出现错误。
(完整word版)高中数学三角函数基础知识点及答案(2),推举文档高中数学三角函数基础知识点及答案1、角的概念的推广：平面内一条射线绕着端点从一具位置旋转到另一具位置所的图形。
按逆时针方向旋转所形成的角叫正角，按顺时针方向旋转所形成的角叫负角，一条射线没有作任何旋转时，称它形成一具零角。
射线的起始位置称为始边，终止位置称为终边。
2、象限角的概念：在直角坐标系中，使角的顶点与原点重合，角的始边与x 轴的非负半轴重合，角的终边在第几象限，就讲那个角是第几象限的角。
假如角的终边在坐标轴上，就以为那个角别属于任何象限。
3. 终边相同的角的表示：(1)α终边与θ终边相同(α的终边在θ终边所在射线上)?2()k kαθπ=+∈Z ，注意：相等的角的终边一定相同，终边相同的角别一定相等.如与角ο1825-的终边相同，且绝对值最小的角的度数是＿＿＿，合＿＿＿弧度。
弧度：一周的弧度数为2πr/r=2π，360°角=2π弧度，所以，1弧度约为57.3°，即57°17'44.806''，1°为π/180弧度，近似值为0.01745弧度，周角为2π弧度，平角（即180°角）为π弧度，直角为π/2弧度。
（答：25-o；536π-）(2)α终边与θ终边共线(α的终边在θ终边所在直线上) ?()k kαθπ=+∈Z . (3)α终边与θ终边对于x 轴对称?2()k k αθπ=-+∈Z . (4)α终边与θ终边对于y 轴对称?2()k k απθπ=-+∈Z . (5)α终边与θ终边对于原点对称?2()k k απθπ=++∈Z .(6)α终边在x 轴上的角可表示为：,k k Z απ=∈；α终边在y 轴上的角可表示为：,2k k Z παπ=+∈；α终边在坐标轴上的角可表示为：,2k k Z πα=∈.如α的终边与6π的终边对于直线x y =对称，则α＝____________。
三角函数、解三角形一、任意角和弧度制及任意角的三角函数1.任意角的概念(1)我们把角的概念推广到任意角，任意角包括正角、负角、零角．①正角：按__逆时针__方向旋转形成的角．②负角：按__顺时针__方向旋转形成的角．③零角：如果一条射线__没有作任何旋转__，我们称它形成了一个零角．(2)终边相同角：与α终边相同的角可表示为：{β|β＝α＋2kπ，k∈Z}，或{β|β＝α＋k·360°，k∈Z}．(3)象限角：角α的终边落在__第几象限__就称α为第几象限的角，终边落在坐标轴上的角不属于任何象限.象限角轴线角2．弧度制(1)1度的角：__把圆周分成360份，每一份所对的圆心角叫1°的角__.(2)1弧度的角：__弧长等于半径的圆弧所对的圆心角叫1弧度的角__.(3)角度与弧度的换算：360°＝__2π__rad,1°＝__π180＝(__180π__)≈57°18′.(4)若扇形的半径为r，圆心角的弧度数为α，则此扇形的弧长l＝__|α|·r__，面积S＝__12|α|r2__＝__12lr__.3．任意角的三角函数定义(1)设α是一个任意角，α的终边上任意一点(非顶点)P的坐标是(x，y)，它与原点的距离为r，则sinα＝__yr__，cosα＝__xr__，tanα＝__yx__.(2)三角函数在各象限的符号是：(3)三角函数线可以看作是三角函数的几何表示．正弦线的起点都在x轴上，余弦线的起点都是原点，正切线的起点都是(1,0)．如图中有向线段MP，OM，AT分别叫做角α的__正弦__线、__余弦__线和__正切__线．4．终边相同的角的三角函数sin(α＋k·2π)＝__sinα__，cos(α＋k·2π)＝__cosα__，tan(α＋k·2π)＝__tanα__(其中k∈Z)，即终边相同的角的同一三角函数的值相等．重要结论1．终边相同的角不一定相等，相等角的终边一定相同，在书写与角α终边相同的角时，单位必须一致．2．确定αk(k∈N*)的终边位置的方法(1)讨论法：①用终边相同角的形式表示出角α的范围．②写出αk的范围．③根据k的可能取值讨论确定αk的终边所在位置．(2)等分象限角的方法：已知角α是第m(m＝1,2,3,4)象限角，求αk是第几象限角．①等分：将每个象限分成k等份．②标注：从x轴正半轴开始，按照逆时针方向顺次循环标上1,2,3,4，直至回到x轴正半轴．③选答：出现数字m的区域，即为αk所在的象限．如α2判断象限问题可采用等分象限法．二、同角三角函数的基本关系式与诱导公式1．同角三角函数的基本关系式(1)平方关系：__sin 2x ＋cos 2x ＝1__. (2)商数关系：__sin xcos x ＝tan x __.2．三角函数的诱导公式1．同角三角函数基本关系式的变形应用：如sin x ＝tan x ·cos x ，tan 2x ＋1＝1cos 2x ，(sin x ＋cos x )2＝1＋2sin x cos x 等． 2．特殊角的三角函数值表“奇变偶不变，符号看象限”．“奇”与“偶”指的是诱导公式k ·π2＋α中的整数k 是奇数还是偶数．“变”与“不变”是指函数的名称的变化，若k 是奇数，则正、余弦互变；若k 为偶数，则函数名称不变．“符号看象限”指的是在k ·π2＋α中，将α看成锐角时k ·π2＋α所在的象限．4.sin x ＋cos x 、sin x －cos x 、sin x cos x 之间的关系sin x ＋cos x 、sin x －cos x 、sin x cos x 之间的关系为(sin x ＋cos x )2＝1＋2sin x cos x ，(sin x －cos x )2＝1－2sin x cos x ，(sin x ＋cos x )2＋(sin x －cos x )2＝2.因此已知上述三个代数式中的任意一个代数式的值，便可求其余两个代数式的值．三、两角和与差的三角函数 二倍角公式1．两角和与差的正弦、余弦和正切公式2．二倍角的正弦、余弦、正切公式 (1)sin2α＝__2sin αcos α__；(2)cos2α＝__cos 2α－sin 2α__＝__2cos 2α__－1＝1－__2sin 2α__； (3)tan2α＝__2tan α1－tan 2α__(α≠k π2＋π4且α≠k π＋π2，k ∈Z )． 3．半角公式(不要求记忆) (1)sin α2＝±1－cos α2； (2)cos α2＝±1＋cos α2；(3)tan α2＝±1－cos α1＋cos α＝sin α1＋cos α＝1－cos αsin α.重要结论1．降幂公式：cos 2α＝1＋cos2α2，sin 2α＝1－cos2α2. 2．升幂公式：1＋cos2α＝2cos 2α，1－cos2α＝2sin 2α. 3．公式变形：tan α±tan β＝tan(α±β)(1∓tan α·tan β)． 1－tan α1＋tan α＝tan(π4－α)；1＋tan α1－tan α＝tan(π4＋α)cos α＝sin2α2sin α，sin2α＝2tan α1＋tan 2α，cos2α＝1－tan 2α1＋tan 2α，1±sin2α＝(sin α±cos x )2.4．辅助角(“二合一”)公式： a sin α＋b cos α＝a 2＋b 2sin(α＋φ)， 其中cos φ＝，sin φ＝ 5.三角形中的三角函数问题在三角形中，常用的角的变形结论有：A ＋B ＝π－C ；2A ＋2B ＋2C ＝2π；A2＋B 2＋C 2＝π2.三角函数的结论有：sin(A ＋B )＝sin C ，cos(A ＋B )＝－cos C ，tan(A ＋B )＝－tan C ，sin A ＋B 2＝cos C 2，cos A ＋B 2＝sin C 2.A >B ⇔sin A >sin B ⇔cos A <cos B .四、三角函数的图象与性质1．周期函数的定义及周期的概念(1)对于函数f(x)，如果存在一个非零常数T，使得当x取定义域内的每一个值时，都有f(x＋T)＝f(x)，那么函数f(x)就叫做__周期函数__.非零常数T叫做这个函数的__周期__.如果在周期函数f(x)的所有周期中存在一个最小的正数，那么这个最小正数就叫做f(x)的最小__正周期__.(2)正弦函数、余弦函数都是周期函数，__2kπ(k∈Z，k≠0)__都是它们的周期，最小正周期是__2π__.2．正弦、余弦、正切函数的图象与性质π重要结论1．函数y ＝sin x ，x ∈[0,2π]的五点作图法的五个关键点是__(0,0)__、__(π2，1)__、__(π，0)__、__(3π2，－1)__、__(2π，0)__.函数y ＝cos x ，x ∈[0,2π]的五点作图法的五个关健点是__(0,1)__、__(π2，0)__、__(π，－1)__、__(3π2，0)__、__(2π，1)__.2．函数y ＝A sin(ωx ＋φ)和y ＝A cos(ωx ＋φ)的最小正周期为T ＝2π|ω|，函数y ＝tan(ωx ＋φ)的最小正周期为T ＝π|ω|.3．正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半周期，相邻的对称中心与对称轴之间的距离是14周期．而正切曲线相邻两对称中心之间的距离是半周期．4．三角函数中奇函数一般可化为y ＝A sin ωx 或y ＝A tan ωx 的形式，而偶函数一般可化为y ＝A cos ωx ＋b 的形式．五、函数y ＝A sin(ωx ＋φ)的图象及应用1．五点法画函数y ＝A sin(ωx ＋φ)(A >0)的图象(1)列表：(2)描点：__(－φω，0)__，__(π2ω－φω，A )__，(πω－φω，0)，(3π2ω－φω，－A )__，(2πω－φω，0)__.(3)连线：把这5个点用光滑曲线顺次连接，就得到y ＝A sin(ωx ＋φ)在区间长度为一个周期内的图象．(4)扩展：将所得图象，按周期向两侧扩展可得y ＝A sin(ωx ＋φ)在R 上的图象2．由函数y ＝sin x 的图象变换得到y ＝A sin(ωx ＋φ)(A >0，ω>0)的图象的步骤3．函数y ＝A sin(ωx ＋φ)(A >0，ω>0，x ∈[0，＋∞)的物理意义 (1)振幅为A . (2)周期T ＝__2πω__.(3)频率f ＝__1T __＝__ω2π__. (4)相位是__ωx ＋φ__. (5)初相是φ.重要结论1．函数y ＝A sin(ωx ＋φ)的单调区间的“长度 ”为T2.2．“五点法”作图中的五个点：①y ＝A sin(ωx ＋φ)，两个最值点，三个零点；②y ＝A cos(ωx ＋φ)，两个零点，三个最值点．3．正弦曲线y ＝sin x 向左平移π2个单位即得余弦曲线y ＝cos x .六、正弦定理、余弦定理1．正弦定理和余弦定理 ①a ＝__2R sin A __，b ＝__2R sin B __，c ＝__2R sin C __；②sin A ＝__a 2R __，sin B ＝__b2R__，sin C＝__c2R __；③ab c ＝__sin Asin B sin C __④a sin B ＝b sin A ，b sin C ＝c sin B ，a sin C ＝c sin Aa <b sin A a ＝b sin A b sin A < a <b a ≥b a >b a ≤b (1)S ＝12a ·h a (h a 表示a 边上的高)．(2)S ＝12ab sin C ＝12ac sin B ＝12bc sin A .(3)S ＝12r (a ＋b ＋c )(r 为内切圆半径)．重要结论在△ABC 中，常有以下结论 1．∠A ＋∠B ＋∠C ＝π.2．在三角形中大边对大角，大角对大边．3．任意两边之和大于第三边，任意两边之差小于第三边．4．sin(A ＋B )＝sin C ；cos(A ＋B )＝－cos C ；tan(A ＋B )＝－tan C ；sin A ＋B 2＝cos C 2，cos A ＋B 2＝sin C 2. 5．tan A ＋tan B ＋tan C ＝tan A ·tan B ·tan C .6．∠A >∠B ⇔a >b ⇔sin A >sin B ⇔cos A <cos B .7．三角形式的余弦定理sin 2A ＝sin 2B ＋sin 2C －2sin B sin C cos A ，sin 2B ＝sin 2A ＋sin 2C －2sin A sin C cos B ，sin 2C ＝sin 2A ＋sin 2B －2sin A sin B cos C .8．若A 为最大的角，则A ∈[π3，π)；若A 为最小的角，则A ∈(0，π3]；若A 、B 、C 成等差数列，则B ＝π3. 9.三角形形状的判定方法(1)通过正弦定理和余弦定理，化边为角(如a ＝2R sin A ，a 2＋b 2－c 2＝2ab cos C 等)，利用三角变换得出三角形内角之间的关系进行判断．此时注意一些常见的三角等式所体现的内角关系，如sin A ＝sin B ⇔A ＝B ；sin(A －B )＝0⇔A ＝B ；sin2A ＝sin2B ⇔A ＝B 或A ＋B ＝π2等． (2)利用正弦定理、余弦定理化角为边，如sin A ＝a 2R ，cos A ＝b 2＋c 2－a 22bc等，通过代数恒等变换，求出三条边之间的关系进行判断．(3)注意无论是化边还是化角，在化简过程中出现公因式不要约掉，否则会有漏掉一种形状的可能．。
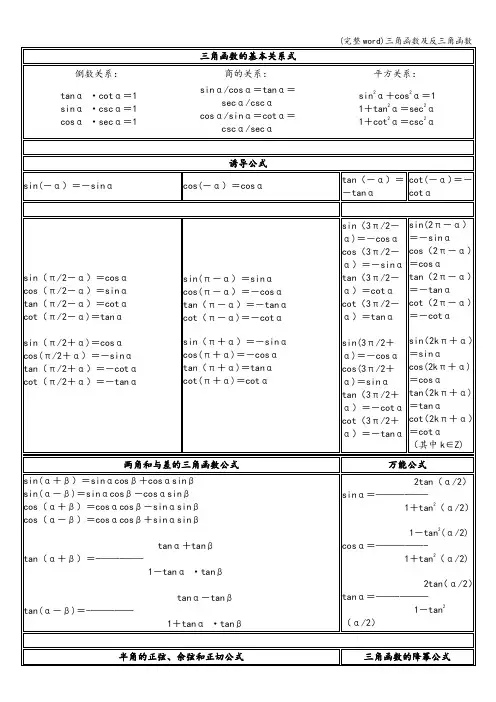
二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α＝2sinαcosαcos2α＝cos2α－sin2α＝2cos2α－1＝1－2sin2α2tanαtan2α＝———-—1－tan2αsin3α＝3sinα－4sin3αcos3α＝4cos3α－3cosα3tanα－tan3αtan3α＝——————1－3tan2α三角函数的和差化积公式三角函数的积化和差公式α＋βα－βsinα＋sinβ＝2sin—－－·cos—－-2 2α＋βα－βsinα－sinβ＝2cos—－－·sin-－—22α＋βα－βcosα＋cosβ＝2cos-－－·cos—－—22α＋βα－βcosα－cosβ＝－2sin—－－·sin—－—22sinα·cosβ=（1/2)［sin(α+β)+sin(α-β）］cosα·sinβ=（1/2)[sin(α+β）—sin(α—β）]cosα·cosβ=(1/2)［cos(α+β)+cos（α—β）］sinα·sinβ=-（1/2）［cos（α+β）—cos(α—β）]化asinα ±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式）函数变换360k+αsinαcosαtanαcotαsecαcscαcosαsinαcotαtanαcscαsecα90°—α90°+αcosα-sinα—cotα—tanα—cscαsecα180°—sinα-cosα—tanα-cotα—secαcscαα—sinα-cosαtanαcotα-secα—cscα180°+α270°--cosα—sinαcotαtanα-cscα—secαα270°+—cosαsinα-cotα-tanαcscα-secαα360°--sinαcosα-tanα-cotαsecα-cscαα﹣α—sinαcosα-tanα—cotαsecα-cscα反三角函数三角函数的反函数，是多值函数。
三角函数相关知识点三角函数知识点学习资料一、基本概念1. 角的概念推广正角、负角和零角：按逆时针方向旋转形成的角为正角，按顺时针方向旋转形成的角为负角，不作任何旋转形成的角为零角。
象限角：使角的顶点与原点重合，角的始边与x轴的非负半轴重合，角的终边落在第几象限，就说这个角是第几象限角。
终边在坐标轴上的角不属于任何象限。
终边相同的角：所有与角α终边相同的角（连同α在内），可构成一个集合S ={β|β=α + k·360^∘,k∈ Z}。
2. 弧度制定义：长度等于半径长的弧所对的圆心角叫做1弧度的角，用符号rad表示。
弧度与角度的换算：180^∘=π rad，所以1^∘=(π)/(180) rad，1 rad = ((180)/(π))^∘。
弧长公式：l =|α|r（其中l为弧长，α为圆心角弧度数，r为半径）。
扇形面积公式：S=(1)/(2)lr=(1)/(2)|α|r^2。
二、三角函数定义设α是一个任意角，它的终边与单位圆交于点P(x,y)，那么sinα=y，cosα = x，tanα=(y)/(x)(x≠0)。
对于角α终边上任意一点P(x,y)（r=√(x^2)+y^{2}），则sinα=(y)/(r)，cosα=(x)/(r)，tanα=(y)/(x)(x≠0)。
2. 三角函数值在各象限的符号正弦函数y = sin x：一、二象限为正，三、四象限为负。
余弦函数y=cos x：一、四象限为正，二、三象限为负。
正切函数y = tan x：一、三象限为正，二、四象限为负。
三、同角三角函数的基本关系1. 平方关系sin^2α+cos^2α = 1。
2. 商数关系tanα=(sinα)/(cosα)(cosα≠0)。
四、诱导公式1. α + 2kπ(k∈ Z)与α的三角函数关系sin(α + 2kπ)=sinα，cos(α+2kπ)=cosα，tan(α + 2kπ)=tanα。
sin(-α)=-sinα，cos(-α)=cosα，tan(-α)=-tanα。
三角函数专题一、核心知识点归纳：1、正弦函数、余弦函数和正切函数的图象与性质：sin y x =cos y x =tan y x =图象定义域 R R,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭值域[]1,1-[]1,1-R最值当22x k ππ=+()k ∈Z 时，max 1y =; 当22x k ππ=-()k ∈Z 时，min 1y =-． 当()2x k k π=∈Z 时，max 1y =；当2x k ππ=+()k ∈Z 时，min 1y =-．既无最大值也无最小值周期性 2π2ππ奇偶性奇函数 偶函数奇函数单调性在2,222k k ππππ⎡⎤-+⎢⎥⎣⎦()k ∈Z 上是增函数;在32,222k k ππππ⎡⎤++⎢⎥⎣⎦ ()k ∈Z 上是减函数．在[]()2,2k k k πππ-∈Z 上是增函数；在[]2,2k k πππ+ ()k ∈Z 上是减函数． 在,22k k ππππ⎛⎫-+ ⎪⎝⎭()k ∈Z 上是增函数．对称性对称中心()(),0k k π∈Z对称中心对称中心函 数 性 质2。
正、余弦定理：在ABC ∆中有: ①正弦定理：2sin sin sin a b cR A B C===（R 为ABC ∆外接圆半径) 2sin 2sin 2sin a R A b R B c R C =⎧⎪=⎨⎪=⎩⇒ sin 2sin 2sin 2a A Rb B Rc C R⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩注意变形应用 ②面积公式：111sin sin sin 222ABC S abs C ac B bc A ∆=== ③余弦定理： 2222222222cos 2cos 2cos a b c bc A b a c ac B c a b ab C ⎧=+-⎪=+-⎨⎪=+-⎩ ⇒ 222222222cos 2cos 2cos 2b c a A bc a c b B ac a b c C ab ⎧+-=⎪⎪+-⎪=⎨⎪⎪+-=⎪⎩二、方法总结：1.三角函数恒等变形的基本策略。
经典三角函数公式及其图像大全三角函数是中学课程里，非常重要的一部分，应将其作为学习的一个重点。
⒈L 弧长=αR=nπR 180 S 扇=21L R=21R 2α=3602R n ⋅π2．S ⊿=21a a h ⋅=21ab C sin =21bc A sin =21ac B sin =Rabc 4=2R 2A sin B sin C sin=AC B a sin 2sin sin 2=B C A b sin 2sin sin 2=C BA c sin 2sin sin 2=pr =))()((c p b p a p p ---(其中)(21c b a p ++=, r 为三角形内切圆半径)3.正弦定理：A a sin =B b sin =Cc sin = 2R （R 为三角形外接圆半径）4.余弦定理：a 2=b 2+c 2-2bc A cos b 2=a 2+c 2-2ac B cosc 2=a 2+b2-2ab C cos bca cb A 2cos 222-+=⒌同角关系：⑴商的关系：①θtg =xy =θθcos sin =θθsec sin ⋅ ②θθθθθcsc cos sin cos ⋅===y x ctg ③θθθtg ry⋅==cos sin ④θθθθcsc cos 1sec ⋅===tg x r ⑤θθθctg rx⋅==sin cos ⑥θθθθsec sin 1csc ⋅===ctg y r ⑵倒数关系：1sec cos csc sin =⋅=⋅=⋅θθθθθθctg tg⑶平方关系：1csc sec cos sin 222222=-=-=+θθθθθθctg tg ⑷)sin(cos sin 22ϕθθθ++=+b a b a（其中辅助角ϕ与点（a,b ）在同一象限，且ab tg =ϕ）⒍函数y=++⋅)sin(ϕωx A k 的图象及性质：（0,0>>A ω） 振幅A ，周期T =ωπ2, 频率f =T1, 相位ϕω+⋅x ，初相ϕ⒎五点作图法：令ϕω+x 依次为ππππ2,23,,20 求出x 与y ，依点()y x ,作图 ⒏诱导公试 三角函数值等于α的同名三角函数值，前面加上一个把α看作锐角时，原三角函数值的符号；即：函数名不变，符号看象限 三角函数值等于α的异名三角函数值，前面加上一个把α看作锐角时，原三角函数值的符号;即：函数名改变，符号看象限⒐和差角公式①βαβαβαsin cos cos sin )sin(±=± ②βαβαβαsin sin cos cos )cos(μ=± ③βαβαβαtg tg tg tg tg ⋅±=±μ1)( ④)1)((βαβαβαtg tg tg tg tg ⋅±=±μ⑤γβγαβαγβαγβαγβαtg tg tg tg tg tg tg tg tg tg tg tg tg ⋅-⋅-⋅-⋅⋅-++=++1)( 其中当A+B+C=π时,有:i).tgC tgB tgA tgC tgB tgA ⋅⋅=++ ii).1222222=++Ctg B tg C tg A tg B tg A tg ⒑二倍角公式：(含万能公式) ①θθθθθ212cos sin 22sin tg tg +== ②θθθθθθθ22222211sin 211cos 2sin cos 2cos tg tg +-=-=-=-=③θθθ2122tg tg tg -= ④22cos 11sin 222θθθθ-=+=tg tg ⑤22cos 1cos 2θθ+=⒒三倍角公式：①)60sin()60sin(sin 4sin 4sin 33sin 3θθθθθθ+︒-︒=-= ②)60cos()60cos(cos 4cos 4cos 33cos 3θθθθθθ+︒-︒=+-=③)60()60(313323θθθθθθθ+⋅-⋅=--=tg tg tg tg tg tg tg ⒓半角公式：（符号的选择由2θ所在的象限确定） ①2cos 12sinθθ-±= ②2cos 12sin 2θθ-= ③2cos 12cos θθ+±= ④2cos 12cos 2θθ+=⑤2sin 2cos 12θθ=- ⑥2cos 2cos 12θθ=+⑦2sin2cos )2sin 2(cos sin 12θθθθθ±=±=±⑧θθθθθθθsin cos 1cos 1sin cos 1cos 12-=+=+-±=tg⒔积化和差公式：[])sin()sin(21cos sin βαβαβα-++=[])sin()sin(21sin cos βαβαβα--+=[])cos()cos(21cos cos βαβαβα-++= ()[]βαβαβα--+-=cos )cos(21sin sin⒕和差化积公式： ①2cos2sin2sin sin βαβαβα-+=+ ②2sin2cos2sin sin βαβαβα-+=-③2cos 2cos 2cos cos βαβαβα-+=+ ④2sin2sin 2cos cos βαβαβα-+-=- ⒖反三角函数： ⒗最简单的三角方程ax =cos1=a {}Z k a k x x ∈+=,arccos 2|π1<a{}Z k a k x x ∈±=,arccos 2|π a tgx = {}Z k arctga k x x ∈+=,|π a ctgx ={}Z k arcctga k x x ∈+=,|π三角、反三角函数图像六个三角函数值在每个象限的符号：sinα·cscα cosα·secα tanα·cotα三角函数的图像和性质：1-1y=sinx-3π2-5π2-7π27π25π23π2π2-π2-4π-3π-2π4π3π2ππ-πoy x1-1y=cosx-3π2-5π2-7π27π25π23π2π2-π2-4π-3π-2π4π3π2ππ-πoyxy=tanx3π2ππ2-3π2-π-π2oyxy=cotx3π2ππ22π-π-π2oyx函数y=sinx y=cosx y=tanxy=cotx定义域R R｛x｜x∈R且x≠kπ+2π,k∈Z｝｛x｜x∈R且x≠kπ,k∈Z｝值域［-1，1］x=2kπ+2π时y max=1x=2kπ-2π时y min=-1［-1,1］x=2kπ时y max=1x=2kπ+π时y min=-1R无最大值无最小值R无最大值无最小值周期性周期为2π周期为2π周期为π周期为π奇偶性奇函数偶函数奇函数奇函数单调性在［2kπ-2π,2kπ+2π］上都是增函数；在［2kπ+2π,2kπ+32π］上都是减函数(k∈Z)在［2kπ-π，2kπ］上都是增函数；在［2kπ，2kπ+π］上都是减函数(k∈Z)在(kπ-2π，kπ+2π)内都是增函数(k∈Z)在(kπ，kπ+π)内都是减函数(k∈Z).反三角函数：arcsinx arccosx名称反正弦函数反余弦函数反正切函数反余切函数。
复习模块: 三角函数知识点1.逆时针方向旋转形成正角, 顺时针方向旋转形成负角, 不旋转形成零角.2、角的终边在第几象限, 就把这个角叫做第几象限的角（或者说这个角在第几象限）．终边在坐标轴上的角叫做界限角3.与角终边相同的角所组成的集合为｛︱｝4.将等于半径长的圆弧所对的圆心角叫做1弧度的角, 记作1弧度或1rad.5、正角的弧度数为正数, 负角的弧度数为负数, 零角的弧度数为零.6.角的弧度数的绝对值等于圆弧长与半径的比, 即（rad）7、换算公式1°= (rad)；1rad (度).30 45 60 90 120 150 180 270 3608、常用角的单位换算:角度制（o）弧度制（rad）9、点为角的终边上的任意一点（不与原点重合）, 点P到原点的距离为,10、则角的正弦、余弦、正切分别定义为: = ； = ；= .11、三角函数值的正负:12.同角三角函数值的关系:,13、常用角的三角函数值:14.诱导公式:=+=++)cos()sin(απαπαπ=-=--)cos()sin(απαπαπ练习题1.将－300o 化为弧度为（ ）A.－43π； B.－53π； C.－76π； D.－74π；2.下列选项中叙述正确的是 （ ） A. 三角形的内角是第一象限角或第二象限角 B. 锐角是第一象限的角 C. 第二象限的角比第一象限的角大 D. 终边不同的角同一三角函数值不相等3.在直角坐标系中, 终边落在x 轴上的所有角是 （ ）. A..B.00与180. C.. D.4.使 有意义的角 是..)A.第一象限的角B.第二象限的角C.第一、二象限的角D.第一、二象限或y 轴的非负半轴上的 5.如果 在第三象限, 则 必定在（）A. 第一或第二象限B. 第一或第三象限C. 第三或第四象限D. 第二或第四象 6.若角 的终边落在直线y=2x 上, 则sin 的值为（ ） . A.... B. ....C.....D.7.一钟表的分针长10 cm, 经过35分钟, 分针的端点所转过的长为 （ ）A. 70 cmB. cmC. ( )cmD. cm8.“sinA=21”是“A=600”的 （ ）A. 充分条件B. 必要条件C. 充分必要条件D. 既不充分也不必要条件 9.如果sin = , （0, ）, 那么cos( － )= （ ） 1312.A135.B 1312.-C 135.-D 10.若A 是三角形的内角, 且sinA= , 则角A 为 （ ）A .450B .1350C .3600k+450D ）450或135011.在△ABC 中, 已知 , 则12. 终边在Ⅱ的角的集合是 13.适合条件|sin α|=－sin α的角α是第 象限角.14.sin = ( 是第二象限角), 则cos = ； tan = 15.sin(-314π)= ; cos 665π=16.已知2sinx+a=3,则a 的取值范围为 已知函数 y=asinx+b （a<0）的最大值为 、最小值为 , 求a 、b 的值. 18、已知tanx=2, 求sinx ·cosx 和 x x x x sin cos sin cos -+的值. 化简: .20.求ππππcos 3tan 314tan 34cos 2++-的值.（1）已知P(12, m)是角 终边上任意 一点, 且 , 求（2）已 知 , 求22.当x为何值时, 函数取得最大值和最小值？分别是多少？。
(完整版)高中三角函数知识点总结高中三角函数知识点总结1. 基本三角函数概念- 三角函数是以单位圆为基础的函数，包括正弦函数、余弦函数和正切函数。
- 正弦函数（sin）：在直角三角形中，对于一个锐角，其对边与斜边的比值称为正弦值。
即：sinA = 对边/斜边。
- 余弦函数（cos）：在直角三角形中，对于一个锐角，其邻边与斜边的比值称为余弦值。
即：cosA = 邻边/斜边。
- 正切函数（tan）：在直角三角形中，对于一个锐角，其对边与邻边的比值称为正切值。
即：tanA = 对边/邻边。
2. 基本三角函数性质和公式- 三角函数的周期性：正弦函数和余弦函数的周期都是2π；正切函数的周期是π.- 三角函数的奇偶性：正弦函数是奇函数，余弦函数是偶函数，正切函数是奇函数。
- 三角函数的同角关系：sinA/cosA = tanA。
- 三角函数的和差化积公式和积化和差公式：具体公式可根据需要进行查阅。
3. 三角函数图像和性质- 正弦函数图像：在0到2π的区间内，正弦函数的图像为一条周期性的波浪线，最高点为1，最低点为-1，对应于最大值和最小值，0点对应于零值。
- 余弦函数图像：在0到2π的区间内，余弦函数的图像为一条周期性的波浪线，最高点为1，最低点为-1，对应于最大值和最小值，0点对应于最大值。
- 正切函数图像：在0到π的区间内，正切函数的图像无法在x=π/2和3π/2时定义，其他点对应的图像为一条连续的射线。
4. 三角函数的应用- 三角函数广泛应用于科学和工程领域中的周期性现象的描述和计算，例如电流的正弦波，声波的波动等。
- 在几何学中，三角函数也应用于测量角度和距离等问题的解决。
以上为高中三角函数的基本知识点总结，更详细的内容和公式可以参考相关教材或资料。
