华附初中趣味数学题

【试题】2019年广东省华师附中数学竞赛专项训练面积及等积变换一、选择题（共8小题，每小题4分，满分32分）1．如图，在梯形ABCD中，AB∥CD，AC与BD交于O，点P在AB的延长线上，且BP ＝CD，则图形中面积相等的三角形有（）A．3对B．4对C．5对D．6对2．如图，点E，F分别是矩形ABCD的边AB，BC的中点，连AF，CE，设AF，CE交于点G，则等于（）A．B．C．D．3．设△ABC的面积为1，D是边AB上一点，且＝，若在边AC上取一点E，使四边形DECB的面积为，则的值为（）A．B．C．D．4．如图，在△ABC中，∠ACB＝90°，分别以AC，AB为边，在△ABC外作正方形ACEF 和正方形AGHB，作CK⊥AB，分别交AB和GH于D和K，则正方形ACEF的面积S1与矩形AGKD的面积S2的大小关系是（）A．S1＝S2B．S1＞S2C．S1＜S2D．不能确定，与的大小有关5．如图，四边形ABCD中∠A＝60°，∠B＝∠D＝90°，AD＝8，AB＝7，则BC+CD等于（）A．B．5C．4D．36．如图，若将左图正方形剪成四块，恰能拼成右图的矩形，设a＝1，则这个正方形的面积为（）A．B．C．D．（1+）27．如图，矩形ABCD中，AB＝a，BC＝b，M是BC的中点，DE⊥AM，E为垂足，则DE ＝（）A．B．C．D．8．O为△ABC内一点，AO、BO、CO及其延长线把△ABC分成六个小三角形，它们的面积如图所示，则S△ABC＝（）A．292B．315C．322D．357二、填空题（共6小题，每小题5分，满分30分）9．如图，梯形ABCD的中位线EF的长为a，高为h，则图中阴影部分的面积为10．如图，若等腰三角形的底边上的高等于18cm，腰上的中线等于15cm，则这个等腰三角形的面积等于．11．如图，在△ABC中，CE：EB＝1：2，DE∥AC，若△ABC的面积为S，则△ADE的面积为．12．如图，已知D、E分别是△ABC的边BC、CA上的点，且BD＝4，DC＝1，AE＝5，EC ＝2．连接AD和BE，它们相交于点P，过点P分别作PQ∥CA，PR∥CB，它们分别与边AB交于点Q、R，则△PQR的面积与△ABC的面积之比为．13．如图，梯形ABCD中，AD∥BC，AD：BC＝2：5，AF：FD＝1：1，BE：EC＝2：3，EF、CD延长线交于G，用最简单的整数比来表示，S△GFD：S△FED：S△DEC＝．14．如图，P是矩形ABCD内一点，若P A＝3，PB＝4，PC＝5，则PD＝．三、解答题（共4小题，满分分48）15．如图，在矩形ABCD中，E是BC上的点，F是CD上的点，S△ABE＝S△ADF＝S矩形ABCD．求：的值．16．一条直线截△ABC的边BC、CA、AB（或它们的延长线）于点D、E、F．求证：．17．如图，在▱ABCD中，P1、P2、P3…P n﹣1是BD的n等分点，连接AP2，并延长交BC 于点E，连接AP n﹣2并延长交CD于点F．（1）求证：EF∥BD；（2）设▱ABCD的面积是S，若S△AEF＝S，求n的值．18．如图，△ABC是等腰三角形，∠C＝90°，O是△ABC内一点，点O到△ABC各边的距离等于1，将△ABC绕点O顺时针旋转45°得到△A1B1C1，两三角形的公共部分为多边形KLMNPQ．①证明：△AKL，△BMN，△CPQ都是等腰直角三角形．②求证：△ABC与△A1B1C1公共部分的面积．参考答案一、选择题（共8小题，每小题4分，满分32分）1．【解答】解：∵AB∥CD则△ABC与△ABD同底等高．∴S△ABC＝S△ABD，S△BCP＝S△ACD又∵BP＝CD∴△BCD与△BCP等底、等高．∴S△BCP＝S△BCD，∴S△ACD＝S△BCD，S△BCP＝S△BCD，S△AOD＝S△BOC，因而共有5对．故选：C．2．【解答】解：连接AC，EF，过B作BM⊥AC，过G作GP⊥AC，延长PG交EF于点Q，∵E、F分别为AB、CB的中点，∴EF为△ABC的中位线，即EF＝AC，EF∥AC，∴BN＝MN＝BM，△EFG∽△CAG，∴QG：PG＝1：2，又PQ＝MN，∴PG＝PQ＝MN＝MB，又△AGC与△ABC都为AC为底边，∴S△AGC：S△ABC＝1：3，则S四边形AGCD＝S△AGC+S△ACD＝（+）S矩形ABCD△＝S矩形ABCD．故选：D．3．【解答】解：连接BE．∵＝，∴△ADE和△ABE的面积比是1：3．设△ADE的面积是k，则△ABE的面积是3k，则△BDE的面积是2k．设△BCE的面积是x，则有（2k+x）＝（3k+x），解得x＝k．则△ABE和△BCE的面积比是3：1，则的值为．故选：B．4．【解答】解：S1＝AC2，S2＝AD•AG，∵∠ADC＝∠ACB＝90°，∠CAD＝∠CAB，∴Rt△ADC∽Rt△ACB，∴，即AC2＝AD•AB，又∵AB＝AG，∴S1＝AC2＝AD•AG＝S2．故选：A．5．【解答】解：如图，延长AB、DC相交于E，在Rt△ADE中，可求得AE2﹣DE2＝AD2，且AE＝2AD，计算得AE＝16，DE＝8，于是BE＝AE﹣AB＝9，在Rt△BEC中，可求得BC2+BE2＝CE2，且CE＝2BC，∴BC＝3，CE＝6，于是CD＝DE﹣CE＝2，BC+CD＝5．故选：B．6．【解答】解：根据图形和题意可得：（a+b）2＝b（a+2b），其中a＝1，则方程是（1+b）2＝b（1+2b）解得：b＝，所以正方形的面积为（1+）2＝．故选：A．7．【解答】解：由矩形ABCD，DE⊥AM可得△ADE∽△ABM，则：＝，得DE＝．8．【解答】解：∵，即，又∵＝＝，即，∴，解之得，∴S△ABC＝84+40+30+35+70+56＝315．故选：B．二、填空题（共6小题，每小题5分，满分30分）9．【解答】解：延长AF交DC的延长线于M，则△ABF≌△MCF，∴AF＝FM，S△ABF＝S△CMF．∴S阴影＝S△DFM，∵AF＝FM，∴S△ADF＝S△MDF，∴，∵S梯形ABCD＝ah，∴S阴影＝ah．10．【解答】解：作MN⊥BC于N，∵AM＝MC，MN∥AD，∴DN＝NC．∴，在Rt△BMN中，BM＝15，MN＝9．∴BN＝12，而BD＝DC＝2DN，∴3DN＝12，DN＝4，∴BC＝16，S△ABC＝AD•BC＝×18×16＝144．11．【解答】解：∵CE：EB＝1：2，设CE＝k，则EB＝2k，∵DE∥AC，而BE：BC＝2k：3k＝2：3，∴，S△BDE＝S∵DE∥AC∴，∴，则S△ADE＝S△BDE＝S．故答案为S．12．【解答】解：如图：过点E作EF∥AD，且交BC于点F，则，∴，∵PQ∥CA，∴，于是，∵PQ∥CA，PR∥CB，∴∠QPR＝∠ACB，∵△PQR∽△CAB，∴．故答案是：．13．【解答】解：设AD＝2，则BC＝5，FD＝1，EC＝3，∵GF：GE＝FD：EC＝1：3，GF：FE＝1：2，S△GFD：S△FED＝GF：FE＝1：2，显然有S△EFD：S△CED＝FD：EC＝1：3，∴S△GFD：S△FED：S△CED＝1：2：6．故答案为：1：2：6．14．【解答】解：过P作AB的平行线分别交DA、BC于E、F，过P作BC的平行线分别交AB、CD于G、H．设AG＝DH＝a，BG＝CH＝b，AE＝BF＝c，DE＝CF＝d，则于是AP2+CP2＝BP2+DP2，又P A＝3，PB＝4，PC＝5，故DP2＝AP2+CP2﹣BP2＝32+52﹣42＝18，则DP＝3．故本题答案为3．三、解答题（共4小题，满分0分）15．【解答】解：设BC＝a，CD＝b，由，得．∴BE＝a，则EC＝a．同理FC＝b，∴，∵，∴，∴，故＝＝5．16．【解答】证明：如图，连接BE、AD，∵△BDE与△DCE等高，∴＝，∵△DCE与△ADE等高，∴＝，∵△ADF与△BDF等高，∴＝，∵△AEF与△BEF等高，∴＝，∴＝，∴••＝••＝1．17．【解答】（1）证明：∵AD∥BC，AB∥DC，∴△P n﹣2FD∽△P n﹣2AB，△P2BE∽△P2DA∴即，∴EF∥BD．（2）解：由①可知，∴，同理可证∴，∴，从而知，已知，∴，即解方程得n＝6．18．【解答】证明：①连接OC、OC1，分别交PQ、NP于点D、E，根据题意得∠COC1＝45°．∵点O到AC和BC的距离都等于1，∴OC是∠ACB的平分线．∵∠ACB＝90°∴∠OCE＝∠OCQ＝45°同理∠OC1D＝∠OC1N＝45°∴∠OEC＝∠ODC1＝90°∴∠CQP＝∠CPQ＝∠C1PN＝∠C1NP＝45°∴△CPQ和△C1NP都是等腰直角三角形．∴∠BNM＝∠C1NP＝45°∠A1QK＝∠CQP＝45°，∵∠B＝45°∠A1＝45°，∴△BMN和△A1KQ都是等腰直角三角形．∴∠B1ML＝∠BMN＝90°，∠AKL＝∠A1KQ＝90°∴∠B1＝45°∠A＝45°∴△B1ML和△AKL也都是等腰直角三角形．②在Rt△ODC1和Rt△OEC中，∵OD＝OE＝1，∠COC1＝45°∴OC＝OC1＝∴CD＝C1E＝﹣1∴PQ＝NP＝2（﹣1）＝2﹣2，CQ＝CP＝C1P＝C1N＝（﹣1）＝2﹣∴延长CO交AB于H∵CO平分∠ACB，且AC＝BC∴CH⊥AB，∴CH＝CO+OH＝+1∴AC＝BC＝A1C1＝B1C1＝（+1）＝2+，∴，∵A1Q＝BN＝（2+）﹣（2﹣2）﹣（2﹣）＝2，∴KQ＝MN＝＝，∴，∵AK＝（2+）﹣（2﹣）﹣＝，∴，。

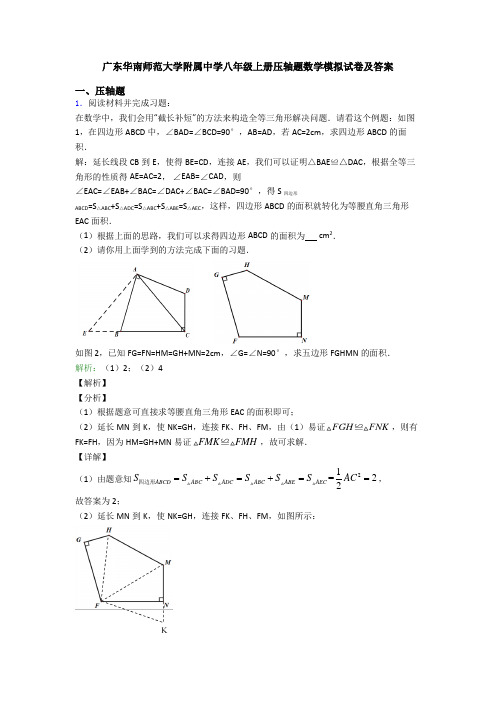
广东华南师范大学附属中学八年级上册压轴题数学模拟试卷及答案一、压轴题1．阅读材料并完成习题：在数学中，我们会用“截长补短”的方法来构造全等三角形解决问题．请看这个例题：如图1，在四边形ABCD 中，∠BAD=∠BCD=90°，AB=AD ，若AC=2cm ，求四边形ABCD 的面积．解：延长线段CB 到E ，使得BE=CD ，连接AE ，我们可以证明△BAE ≌△DAC ，根据全等三角形的性质得AE=AC=2， ∠EAB=∠CAD ，则∠EAC=∠EAB+∠BAC=∠DAC+∠BAC=∠BAD=90°，得S 四边形ABCD =S △ABC +S △ADC =S △ABC +S △ABE =S △AEC ，这样，四边形ABCD 的面积就转化为等腰直角三角形EAC 面积．（1）根据上面的思路，我们可以求得四边形ABCD 的面积为 cm 2．（2）请你用上面学到的方法完成下面的习题．如图2，已知FG=FN=HM=GH+MN=2cm ，∠G=∠N=90°，求五边形FGHMN 的面积． 解析：（1）2；（2）4【解析】【分析】（1）根据题意可直接求等腰直角三角形EAC 的面积即可；（2）延长MN 到K ，使NK=GH ，连接FK 、FH 、FM ，由（1）易证FGH FNK ≌，则有FK=FH ，因为HM=GH+MN 易证FMK FMH ≌，故可求解．【详解】（1）由题意知21=22ABC ADC ABC ABE AEC ABCD AC S SS S S S =+=+==四边形， 故答案为2；（2）延长MN 到K ，使NK=GH ，连接FK 、FH 、FM ，如图所示：FG=FN=HM=GH+MN=2cm ，∠G=∠N=90°，∴∠FNK=∠FGH=90°，∴FGH FNK ≌，∴FH=FK ， 又FM=FM ，HM=KM=MN+GH=MN+NK ，∴FMK FMH ≌，∴MK=FN=2cm ， ∴12=242FGH HFM MFN FMK FGHMN S SS S S MK FN =++=⨯⋅=五边形． 【点睛】本题主要考查全等三角形的性质与判定，关键是根据截长补短法及割补法求面积的运用．2．（1）发现：如图1，ABC ∆的内角ABC ∠的平分线和外角ACD ∠的平分线相交于点O 。

⼴东省⼴州市华南师范⼤学附属中学2023-2024学年⼋年级上学期期中数学试题⼀、单选题1．下列各式中，计算结果等于a2的是（）A．a2⋅a3B．a5÷a3C．a2+a3D．a5−a02．在下列各式中，应填⼊“−y”的是（）A．−y3⋅______=−y B．−2y3⋅______=2y4C．−2y3⋅______=−8y4D．−y12⋅______=−3y133．如图，CD，CE，CF分别是△ABC⾼，⻆平分线、中线，则下列各式中错误的是（）A．BA=2BF B．∠ACE=1∠ACB2C．AE=BE D．CD⊥AB4．如图，BD是∠ABC的⻆平分线，AD⊥BD，垂⾜为D，∠DAC=20°，∠C=38°，则∠BAD=（）A．58°B．64°C．62°D．56°5．如图，将透明直尺叠放在正五边形徽章ABCDE上，若直尺的下沿MN⊥DE于点O，且经过点B，上沿PQ经过点E，则∠ABM的度数为（）A．152°B．126°C．120°D．108°6．已知下图中的两个三⻆形全等，则∠α等于（）A．72°B．58°C．60°D．50°7．如图，已知∠1=∠2，则下列条件中，不能使△ABC≌△DCB成⽴的是（）A．AB=CD B．AC=BDC．∠A=∠D D．∠ABC=∠DCB8．使x2+mx2−2x+n的乘积不含x3和x2，则m、n的值为()A．m=0，n=0B．m=−2，n=−4C．m=−2，n=4D．m=2，n=49．图中△ABC≌△ADE,∠DAC=100°,∠BAE=140°，则∠CFE的度数是（）A．15°B．20°C．25°D．30°10．如图，在△ABC中，BO，CO分别平分∠ABC，∠ACB，且交于点O，CE为外⻆∠ACD的平分线，BO的延⻓线交CE于点E，则以下结论：①∠A=2∠E；②∠BOC= 3∠E；③∠BOC=90°+∠A；④∠BOC=90°+∠E．正确的是（）A．①④B．①③④C．①②③D．①②④⼆、填空题11．计算a a−c的结果是．12．如果⼀个多边形的内⻆和是1800度，它是边形．13．三⻆形三边⻓为7cm、12cm、a cm，则a的取值范围是．14．计算：1−1−=．15．如图，AB∥CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且与AB垂直．若点P到BC的距离是4，则AD的⻓为．16．如图，AD是△ABC的中线，E，F分别是AD和AD延⻓线上的点，且DE=DF，连接BF，CE，下列说法：①△ABD和△ACD⾯积相等；②∠BAD=∠CAD；③△BDF≌△CDE；④BF∥CE；⑤CE=AE．其中正确的是．三、解答题17．计算：(1)2x+1x−2；(2)6x4−8x3÷−2x2．18．⼩明和⼩军两⼈共同计算⼀道整式乘法题：2x+a⋅3x+b，由于⼩明错把a前的加号抄成减号，得到的结果为6x2−13x+6，⼩军由于漏抄了第⼆个多项式中x的系数，得到的结果为2x2−x−6，请你计算出这道整式乘法题的正确答案．19．如图，点A，B，C，D在同⼀条直线上，点E，F分别在直线AB的两侧，且AE=BF，∠A=∠B，AD=BC．(1)求证：△ACE≌△BDF；(2)若AB=8,AC=2，求CD的⻓．20．如图，已知△ABC的三个顶点的坐标分别为A−2,3、B−6,0、C−1,0．(1)将△ABC沿y轴翻折，则翻折后点A的对应点的坐标是．(2)若以D、B、C为顶点的三⻆形与△ABC全等，请画出所有符合条件的△DBC（点D 与点A重合除外），并直接写出点D的坐标．21．在△ABC中，AB=AC，AC边上的中线BD把三⻆形的周⻓分成12cm和15cm的两部分，求三⻆形各边的⻓．22．已知，如图，AD∥BC，AE平分∠BAD，点E是CD的中点.（1）求证：AB=AD＋BC（2）求证：AE⊥BE23．我们知道，⼀般的数学公式、法则、定义可以正向运⽤，也可以逆向运⽤．对于“同底数幂的乘法”“幂的乘⽅”“积的乘⽅”这⼏个法则的逆向运⽤表现为a m+n=a m·a n，a mn=a m n=a n m，a mb m=ab m；（m，n为正整数）．请运⽤这个思路和幂的运算法则解决下列问题：(1)已知a=255，b=344，c=433，请把a，b，c⽤“<”连接起来：；(2)若x a=2，x b=3，求x3a+2b的值；(3)计算：2100×8101．24．如图，在△ABC中，AB=AC，点P从点B出发沿线段BA移动，同时，已知点Q 从点C出发沿线段AC的延⻓线移动，点P，Q移动的速度相同，PQ与直线BC相交于点D．(1)求证：PD=QD(2)过点P作直线BC的垂线．重⾜为E，P，Q在移动的过程中，线段DE是否为⻓度保持不变的线段?请说明理由．25．如图所示，⻓⽅形ABCD中，AB=4cm,AD=8cm．点P从点A出发沿边AD向A−D−A做往返运动，每秒移动2cm，动直线a与边CD重合，交AD于点M、BC于点N．直线a与点P同时出发，沿DA⽅向移动，每秒移动1cm，移动t秒t>0，当直线a与边AB重合时，移动全部停⽌．(1)⽤含t的代数式表示AP的⻓度：(2)当t为何值时，点P在直线a上；(3)连接PB,PN，直接写出当t为何值时，△PAB与△PMN全等．参考答案：题号12345678910答案B B C A B D A D B A1．B【分析】分别利⽤合并同类项法则以及同底数幂的乘法运算法则和幂的乘⽅运算法则分别计算即可．【详解】解：a2⋅a3=a5，故选项A不符合题意；a5÷a3=a2，故选项B符合题意；a2+a3⽆法合并同类项，故选项C不符合题意；a5−a0=a5−1，故选项D不符合题意．故选B．【点睛】本题主要考查合并同类项法则以及同底数幂的乘法运算法则和幂的乘⽅运算法则，熟练掌握运算法则是解题的关键．2．B【分析】根据单项式乘单项式的法则，可得答案．【详解】解：A．−y3⋅y−2=−y，故选项不符合题意；B．−2y3⋅−y=2y4，故选项符合题意；C．(−2y)3⋅y=−8y4，故选项不符合题意；D．(−y)12⋅−3y=−3y13，故选项不符合题意．故选：B．【点睛】本题考查了单项式乘单项式，系数乘系数，同底数幂相乘，在⼀个单项式中出现的字⺟作为积的⼀个因式出现，注意符号．3．C【分析】本题主要考查了三⻆形⾼，中线，⻆平分线的定义，熟知相关定义是解题的关键．根据三⻆形⾼，中线，⻆平分线的定义进⾏逐⼀判断即可．【详解】解：A、∵CF是△ABC的中线，∴AB=2BF，原结论正确，不符合题意；B、∵CE是△ABC的⻆平分线，∴∠ACE=1∠ACB，原结论正确，不符合题意；2C、∵CF是△ABC的中线，∴AF=BF，∴AF−EF=AE<BF+EF=BE，原结论错误，符合题意；D、∵CD是△ABC的⾼，∴CD⊥AB，原结论正确，不符合题意；故选：C．4．A【分析】因为BD是∠ABC的⻆平分线，所以∠ABD=∠CBD=12∠ABC，由AD⊥BD，得∠ADB=90°，则∠BAD=90°−12∠ABC，在△ABC中，∠ABC+∠C+∠BAD+∠DAC=180°，即可作答【详解】解：因为BD是∠ABC的⻆平分线，所以∠ABD=∠CBD=12∠ABC，由AD⊥BD，得∠ADB=90°，在△ABD中，∠BAD=180°−90°−∠ABD=90°−12∠ABC，因为在△ABC中，∠ABC+∠C+∠BAD+∠DAC=180°，把∠DAC=20°，∠C=38°代⼊，得∠ABC+38°+90°−12∠ABC+20°=12∠ABC+148°=180°那么∠ABC=64°，所以∠BAD=90°−12×64°=58°，故选：A．【点睛】本题考查了三⻆形内⻆和为180°以及⻆平分线的定义，难度较⼩．5．B【分析】利⽤多边形的内⻆和及正多边形的性质求得∠AED，∠A的度数，然后结合已知条件及四边形的内⻆和求得∠ABO的度数，从⽽求得∠ABM的度数．【详解】解：由题意可得∠AED=∠A=5−2×180°÷5=108°，∵MN⊥DE，∴∠BOE=90°，∴四边形ABOE中，∠ABO=360°−90°−108°−108°=54°，∴∠ABM=180°−∠ABO=180°−54°=126°，故选：B．【点睛】本题考查多边形的内⻆和，结合已知条件求得各⻆之间的关系和度数是解题的关键．6．D【分析】本题考查了全等三⻆形的性质，根据全等三⻆形对应⻆相等解答即可．【详解】解：∵两个三⻆形全等，∴a，c两边的夹⻆相等，∴∠α=50°，故选：D．7．A【分析】本题考查三⻆形全等的判定，根据三⻆形的判定逐个判断即可得到答案；【详解】解：当AB=CD时，AB=CD不能判断三⻆形全等，故符合题意，BC=BC∠2=∠1当AC=BD时，AC=BD满⾜边⻆边判定，能判断三⻆形全等，故不符合题意，∠2=∠1BC=BC当∠A=∠D时，∠A=∠D满⾜⻆⻆边判定，能判断三⻆形全等，故不符合题意，∠2=∠1BC=BC当AC=BD时，∠ABC=∠DCB满⾜⻆边⻆判定，能判断三⻆形全等，故不符合题意，BC=BC∠2=∠1故选：A．8．D【分析】原式利⽤多项式乘以多项式法则计算，根据乘积不含x3和x2项，求出m与n的值即可．【详解】解：原式=x4−2x3+nx2+mx3−2mx2+mnx=x4+m−2x3+n−2m x2+mnx，因为乘积不含x3和x2项，得到m−2=0，n−2m=0，解得：m=2，n=4，故选：D．【点睛】此题考查了多项式乘多项式，熟练掌握公式及法则是解本题的关键．9．B【分析】先根据全等三⻆形对应⻆相等求出∠B=∠D,∠BAC=∠DAE，所以∠BAD=∠CAE，然后求出∠BAD的度数，再根据△ABG和△FDG的内⻆和即可求出．【详解】解：∵△ABC≌△ADE，∴∠B=∠D,∠BAC=∠DAE，∵∠BAD=∠BAC−∠CAD，∠CAE=∠DAE−∠CAD，∴∠BAD=∠CAE，∵∠DAC=100°,∠BAE=140°，∴∠BAD=12(∠BAE−∠DAC)=20°，在△ABG和△FDG中，∠B=∠D,∠AGB=∠FGD，∴∠DFB=∠BAD=20°，∴∠CFE=∠DFB=20°，故选：B．【点睛】本题考查全等三⻆形的性质，灵活运⽤所学知识是关键．10．A【分析】本题考查了三⻆形内⻆和定理，⻆平分线，外⻆的性质等知识，由⻆平分线的定义可得∠DCE=12∠ACD，∠DBE=12∠ABC，∠OBC=12∠ABC，∠OCB=12∠ACB，再根据三⻆形内⻆和，外⻆性质即可判断，明确⻆度之间的数量关系是解题的关键．【详解】解：①∵CE为外⻆∠ACD的平分线，BE平分∠ABC，∴∠DCE=12∠ACD，∠DBE=12∠ABC，⼜∵∠DCE是△BCE的外⻆，∴∠E=∠DCE−∠DBE=12(∠ACD−∠ABC)=12∠A，故①正确，∵BO，CO分别平分∠ABC，∠ACB∴∠OBC=12∠ABC，∠OCB=12∠ACB，∴∠BOC=180°−(∠OBC+∠OCB)=180°−12(∠ABC+∠ACB)=180°−12(180°−∠A)=90°+12∠A，故②③错误，∵OC平分∠ACB，CE平分∠ACD，∴∠ACO=12∠ACB，∠ACE=12ACD，∴∠OCE=12(∠ACB+∠ACD)=12×180°=90°，∴∠BOC是△COE的外⻆，∴∠BOC=∠OCE+∠E=90°+∠E，故④正确，综上所述正确的结论是①④，故选：A．11．a2−ac/−ac+a2【分析】根据单项式乘以多项式的计算法则求解即可．【详解】解：a a−c=a2−ac，故答案为：a2−ac．【点睛】本题主要考查了单项式乘以多项式，熟知相关计算法则是解题的关键．12．⼗⼆【分析】利⽤多边形内⻆和公式进⾏求解即可．【详解】解：设多边形的边数为n，n−2×180°=1800°，解得：n=12，故答案为：⼗⼆．【点睛】本题考查了多边形的内⻆和，解题关键是牢记多边形的内⻆和公式，边数为n的多边形的内⻆和为n−2×180°．13．5＜a＜19．【详解】解：根据三⻆形中：任意两边之和＞第三边，任意两边之差＜第三边，即可求解．试题解析：a的范围是：12-7＜a＜12+7，即5＜a＜19．考点：三⻆形三边关系．14．1120/0.55【分析】接利⽤平⽅差公式把每⼀个算式因式分解，再进⼀步发现规律计算即可．【详解】解：原式=1−1−=1++⋯+1+=32×12×43×23×54×34×⋯×109×89×1110×910=12×1110=1120，故答案为：1120．【点睛】此题考查因式分解的应⽤，解题关键在于利⽤公式进⾏计算．15．8【分析】过点P作PE⊥BC，根据平⾏线的性质可得PD⊥CD，⼜根据⻆平分线的性质可得PE=PA=PD，进⽽可求解．【详解】解：过点P作PE⊥BC，如图：∵点P到BC的距离是4，∴PE=4，∵AB∥CD，PA⊥AB，∴PD⊥CD，∵BP和CP分别平分∠ABC和∠DCB，∴PA=PE=4，PD=PE=4，∴AD=PA+PD=4+4=8，故答案为：8．【点睛】本题考查了平⾏线的性质及⻆平分线的性质，熟练掌握其性质是解题的关键．16．①③④【分析】根据三⻆形的中线，等底等⾼的三⻆形⾯积相等即可判断出①正确；根据三⻆形的中线得BD=CD，即∠BAD不⼀定和∠CAD相等，则②错误；利⽤边⻆边可证明△BDF≌△CDE，可判断出③正确；根据全等三⻆形的性质得∠F=∠DEC，则BF∥CE，可判断出④正确，⑤错误，即可得．【详解】解：∵AD是△ABC的中线，∴BD=CD，∴△ABD和△ACD⾯积相等，故①正确；∵AD是△ABC的中线，∴BD=CD，∴∠BAD不⼀定和∠CAD相等，否则可以证明AB=AC，故②错误；在△BDF和△CDE中，BD=CD，∠BDF=∠CDEDE=DF∴△BDF≌△CDE SAS，故③正确；∵△BDF≌△CDE，∴∠F=∠DEC，∴BF∥CE，故④正确；∵△BDF≌△CDE，∴CE=BF，条件不⾜，⽆法证明CE=AE，故⑤错误；综上，①③④正确，故答案为①③④．【点睛】本题考查了中线，全等三⻆形的判定与性质，平⾏线的判定，解题的关键是理解题意，掌握这些知识点．17．(1)2x2−3x−2；(2)−3x2+4x【分析】（1）直接根据多项式与多项式的乘法法则计算即可；（2）根据多项式与单项式的除法法则计算．【详解】（1）解：2x+1x−2=2x2+x−4x−2=2x2−3x−2；（2）解：6x4−8x3÷−2x2=6x4÷−2x2−8x3÷−2x2=−3x2+4x．【点睛】此题主要考查整式的乘除运算，解题的关键是熟知整式的运算法则．18．6x2+5x−6【分析】根据⼩明的计算结果推出3a−2b=13，根据⼩军的计算结果得到a+2b=−1，由此建⽴⽅程组求出a、b的值，再根据多项式乘以多项式的计算法则求解即可．【详解】解：∵⼩明错把a前的加号抄成减号，得到的结果为6x2−13x+6，∴2x−a⋅3x+b=6x2−13x+6，∴6x2−3ax+2bx−ab=6x2−13x+6，∴6x2−3a−2b x−ab=6x2−13x+6，∴3a−2b=13①，∵⼩军由于漏抄了第⼆个多项式中x的系数，得到的结果为2x2−x−6，∴2x+a⋅x+b=2x2−x−6，∴2x2+ax+2bx+ab=2x2−x−6，∴2x2+a+2b x+ab=2x2−x−6，∴a+2b=−1②，联⽴①②得3a−2b=13a+2b=−1，解得a=3b=−2，∴2x+a⋅3x+b=2x+3⋅3x−2=6x2+9x−4x−6=6x2+5x−6．【点睛】本题主要考查了多项式乘以多项式，熟知多项式乘以多项式的计算法则是解题的关键．19．(1)⻅解析(2)4【分析】题⽬主要考查全等三⻆形的判定和性质，（1）直接利⽤SAS证明△ACE≌△BDF即可；（2）根据全等三⻆形的性质得到BD=AC=2，则AD=AB−BD=8−2=6，熟练掌握全等三⻆形的判定和性质是解题关键．【详解】（1）证明：∵AD=BC，∴AD−CD=BC−CD，即AC=BD，在△ACE和△BDF中，AC=BD，∠A=∠BAE=BF∴△ACE≌△BDF SAS；（2）解：∵△ACE≌△BDF，AC=2，∴BD=AC=2，⼜∵AB=8，∴CD=AB−BD−AC=8−2−2=4．20．(1)2,3(2)D−2,−3或D−5,3或D−5,−3【分析】（1）直接利⽤关于y轴对称点的性质得出对应点位置；（2）直接利⽤全等三⻆形的判定⽅法得出对应点位置．【详解】（1）解：如图所示，△A1B1C1即为所求；∴翻折后点A的对应点的坐标是：2，3；故答案为：2，3；（2）解：如图所示，D1−2,−3或D2−5,3或D3−5,−3即为所求．【点睛】此题主要考查了轴对称变换以及全等三⻆形的判定，正确得出对应点位置是解题关键．21．三⻆形的各边⻓为10cm、10cm、7cm或8cm、8cm、11cm【分析】由在△ABC中，AB=AC，AC边上的中线BD把三⻆形的周⻓分成12cm和15cm两部分，可得|AB−BC|=15−12=3cm，AB+BC+AC=2AB+BC= 12+15=27cm，然后分别从AB>BC与AB<BC去分析求解即可求得答案．【详解】解：如图，∵AB=AC，BD是AC边上的中线，即AD=CD，∴|AB+AD−BC+CD|=|AB−BC|=15−12=3cm，AB+BC+AC= 2AB+BC=12+15=27cm，若AB>BC，则AB−BC=3cm，⼜∵2AB+BC=27cm，联⽴⽅程组:AB−BC=3,2AB+BC=27解得：AB=10cm，BC=7cm，10cm、10cm、7cm三边能够组成三⻆形；若AB<BC，则BC−AB=3cm，⼜∵2AB+BC=27cm，联⽴⽅程组BC−AB=3,2AB+BC=27解得：AB=8cm，BC=11cm，8cm、8cm、11cm三边能够组成三⻆形；∴三⻆形的各边⻓为10cm、10cm、7cm或8cm、8cm、11cm．【点睛】此题考查了等腰三⻆形的定义．注意掌握⽅程思想、分类讨论思想与数形结合思想的应⽤．22．（1）答案⻅解析；（2）答案⻅解析.【分析】(1)延⻓AE交BC的延⻓线于点F，根据⻆平分线和平⾏线的性质得到∠BAF=∠F，然后等⻆对等边AB=BF，再证明△FCE≌△ADE，进⽽等量代换求解；(2)由全等得出AE=EF，然后利⽤等腰三⻆形三线合⼀的性质，即可得结论；【详解】解：如图：延⻓AE交BC的延⻓线于点F，∵AE平分∠BAD∴∠BAF=∠DAE∵E是DC中点∴DE=CE∵AD∥BC∴∠DAE=∠F∴∠BAF=∠F∴AB=BF⼜∵在△FCE和△ADE中，∠DAE=∠F ∠DEA=∠CEF DE=CE∴△FCE≌△ADE，∴AD=CF∴AB=BF=BC+CF=BC+AD即AB=AD＋BC（2）由（1）可知△FCE≌△ADE∴AE=FE⼜∵BA=BF∴根据等腰三⻆形三线合⼀的性质可知AE⊥BE.【点睛】本题考查平⾏线的性质，等腰三⻆形的性质和判定，全等三⻆形的性质和判定，根据题意适当作出辅助线是解题关键.23．(1)a<c<b(2)72(3)8【分析】（1）根据逆⽤幂的乘⽅，化成指数相同的幂，再⽐较⼤⼩；（2）根据逆⽤同底数幂的乘法和逆⽤幂的乘⽅即可求解；（3）根据逆⽤同底数幂的乘法和逆⽤幂的乘⽅，化成指数相同的幂，再计算即可求解；本题主要考查了同底数幂的乘法、幂的乘⽅法则，掌握法则的逆⽤是解题的关键．【详解】（1）解：∵a=255=2511=3211，b=344=3411=8111，c=433＝4311=6411．⼜∵32<64<81，∴a<c<b，故答案为：a<c<b；（2）解：x3a+2b=x3a⋅x2b，=x a3⋅x b2，∵x a=2，x b=3，∴原式=23⋅32，=8×9，=72；（3）解：2100×8101×=2100×23101×2200，=2100×2303，=2403×，=2400×23，=2×23，=1402×23，=8．24．(1)⻅解析(2)线段DE是⻓度保持不变的线段，理由⻅解析【分析】（1）过点P作PF∥AC交BC于F，根据题意可知BP=CQ，由平⾏线的性质以及等腰三⻆形的性质可推导∠B=∠PFB，即可证明PF=CQ，然后证明△PFD≌△QCD，由全等三⻆形的性质证明PD=QD即可；（2）由（1）可知，BP=PF，由等腰三⻆形“三线合⼀”的性质可知BE=EF，再由全等三⻆形的性质证明FD=DC，即可推导DE=1BC，即DE为定值．2【详解】（1）证明：过点P作PF∥AC交BC于F，如下图，∵点P、Q同时出发，且移动的速度相同，∴BP=CQ，∵PF∥AC，∴∠PFB=∠ACB,∠DPF=∠Q，∵AB=AC，∴∠B=∠ACB，∴∠B=∠PFB，∴BP=PF，∴PF=CQ，在△PFD和△QCD中，∠PDF=∠QDC，PF=CQ∠DPF=∠Q∴△PFD≌△QCD(ASA)，∴PD=QD；（2）解：DE的⻓度保持不变，理由如下：由（1）可知，BP=PF，∵PE⊥BF，∴BE=EF，由（1）可知，△PFD≌△QCD，∴FD=DC，∴DE=EF+DF=BE+DC=1BC，2∴DE为定值．【点睛】本题主要考查了全等三⻆形的判定与性质、等腰三⻆形的判定与性质、平⾏线的性质等知识，理解题意，正确作出辅助线是解题关键．25．(1)2t或16−2t；或8(2)83(3)85【分析】（1）根据题意，分两种情况讨论即可求解；（2）由题意可知，当点P在直线a上时，点P与点M重合，即AP+DM=AD=8，分两种情况讨论，列⼀元⼀次⽅程求解即可；（3）由题意可知，当AP=MP时，△PAB与△PMN全等，分两种情况讨论，分别表示出MP的⻓，再列⼀元⼀次⽅程求解即可．【详解】（1）解：由题意可知，AD=8cm，点P每秒运动2cm，当点P沿AD⽅向运动时，AP=2t；答案第15⻚，共15⻚当点P 沿DA ⽅向运动时，AP =16−2t ；综上可知，AP 的⻓度为2t 或16−2t ；（2）解：由题意可知，动直线a 交AD 于点M ，沿DA ⽅向运动，每秒运动1cm ，∴DM =t ，当点P 在直线a 上时，点P 与点M 重合，即AP +DM =AD =8，当0<t ≤4时，此时点P 沿AD ⽅向运动，AP =2t ，则2t +t =8，解得；t =83；当4<t ≤8时，此时点P 沿DA ⽅向运动，AP =16−2t ，则16−2t +t =8，解得：t =8，综上可知，当t 为83或8时，点P 在直线a 上；（3）解：由题意可知，AB =MN ，∠BAP =∠NMP =90°，∴当AP =MP 时，△PAB 与△PMN 全等，当0<t ≤4时，此时点P 沿AD ⽅向运动，AP =2t ，DM =t∴MP =AD −AP −DM =8−2t −t =8−3t ，∴2t =8−3t ，解得：t =85；当4<t ≤8时，此时点P 沿DA ⽅向运动，AP =16−2t ，DM =t∴MP =AD −AP −DM =8−16−2t −t =t −8，∴16−2t =t −8，解得：t =8，此时△PAB 与△PMN 不存在，不符合题意，∴当t 为85时，△PAB 与△PMN 全等．【点睛】本题考查了动点问题，⼀元⼀次⽅程的应⽤，全等三⻆形的判定，利⽤分类讨论的思想解决问题是解题关键．。

广东华南师范大学附属中学新初一分班数学试卷一、选择题1．在一幅地图上用3厘米的线段表示120千米的实际距离，这幅地图的比例尺是（）。

A．1∶40 B．1∶400000 C．1∶40000002．小郑有两个正方形骰子，每个面上点数符合如下规则：骰子相对两个面上的点数之和为7．下面是四个骰子的展开图．其中哪两个可能是小郑的骰子？A．Ⅰ和ⅡB．Ⅱ和ⅢC．Ⅲ和ⅣD．Ⅰ和Ⅳ3．把一段圆柱形钢材削成一个最大的圆锥体，切掉的部分重12千克，求原钢材重多少千克？正确的算式是（）A．12÷B．12×3 C．12÷D．12×24．一个三角形三个角度数的比是2:2:5，这个三角形是（）。

A．等腰三角形B．等边三角形C．直角三角形D．等腰直角三角形5．六年级学生参加科技小组有31人，比文艺小组人数的2倍还多3人，文艺小组有多少人？下列方程正确的是（）。

A．2x＋3＝31 B．2x－3＝31 C．x÷2＋3＝31 D．x÷2－3＝316．下图是一个正方体展开图，与4号相对的面是（）号．A．6 B．5 C．2 D．17．下面说法错误的是（）。

A．在367个同学中至少有2个同学是同年同月同日出生的B．真分数小于1，假分数大于1C．0既不是正数，又不是负数，但它是整数，还是自然数D．三角形的面积一定，底和高成反比例8．一个圆柱的底面直径扩大到原来的2倍，高不变，这个圆柱的侧面积就扩大到原来的（）。

A．2倍B．3倍C．4倍D．5倍9．一件商品提价10％以后又降价10％，现在这件商品的价格是原来价格的百分之几？正确的解答是（）A．110％B．90％C．100％D．99％10．动脑筋,做一做．如下图,将一张正方形纸先上下对折压平,再左右对折压平,得到正方形ABCD,取AB 的中点M 和BC 的中点N,剪掉三角形MBN,得到五边形AMNCD ．将折叠的五边形AMNCD 纸片展开铺平后的图形是( )．A ．B ．C ．D ．二、填空题11．0.05升＝（________）立方厘米 35小时＝（________）分 1.2公顷＝（________）公顷（________）平方米十12．()()()()3812:0.75%÷====。

广州市华附奥校新初一分班数学试卷含答案一、选择题1．一个零件长4毫米，画在图上长12厘米。

这幅图的比例尺是（ ）。

A ．1∶30B ．1∶3C ．30∶1D ．3∶12．如图所示是一个正方体展开图，和这个展开图对应的正方体是（ ）A ．B ．C ．D ．3．一桶油用去35千克，还剩15千克，剩下的比用去的少百分之几？正确的算式是（ ）。

A ．()351535-÷ B ．()353515÷+ C ．()153515÷+D ．1535÷4．有一个等腰三角形，其中两个角的度数之比是1∶2。

这个三角形按角分不可能是（ ）。

A ．锐角三角形B ．直角三角形C ．钝角三角形5．如果x 是一个大于0的数，那么x ＋79和x×79比较的结果是（ ）。

A ．x×79大B ．x ＋79大C ．无法确定6．下图是一个正方体的展开图，在这个正方体中，和“美”相对的面是（ ）。

A ．建B ．晋C ．丽D ．城7．铁路提速后，从甲地到乙地时间由16小时缩短到10小时，下列说法错误的是（ ）。

A ．速度比原来提高60% B ．时间比原来减少37.5% C ．现在速度是原来的62.5%D ．现在与原来速度比是8∶58．图中，将长方形绕直线L 旋转一周形成一个圆柱，这个圆柱的底面积是（ ）cm 2。

A ．3.14B ．12.56C ．78.59．一种商品提价20%后，又降价20%，现在的价格（ ）。

A．与原价相同B．比原价低C．比原价高10．古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”，而把1、4、9、16…这样的数称为“正方形数”，从图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中，符合这一规律的是（）A．13=3+10 B．25=9+16 C．36=15+21 D．49=18+31二、填空题11．3.2时＝（______）时（______）分 5千克80克＝（______）千克十12．（________）÷24＝14∶（________）＝78＝（________）%。

九年级数学练习题(综合练习三)班级 座号 姓名 成果一、填空题：（每小题3分，共36分） 1．－2的相反数是 ．2．分解因式：=-x x 2． 3．函数1-=x y 中，自变量x 的取值范围是 ．4．爱须要从小事做起，假如人人都向“盼望工程”捐款1毛钱，全中国的捐款数额将会超过130000000元，这些钱将使很多失学儿童重返学校，用科学记数表示这一数据为 ．5．不等式组：的解集为 ． 6．一个多边形的内角和及它的外角和相等，则这个多边形的边数是 ． 7．写出一个既是轴对称图形，又是中心对称图形的图形： ． 8．抛物线()3122+-=x y 的顶点坐标是 .9．从10000名初三学生中，随机地抽取100名学生，测得他们所穿鞋的鞋号（单位：公分），则这个样本数据的平均数、中位数、众数、方差四个指标中，鞋厂最感爱好的指标是 .10．如右图的转盘中，图中面积大小一样的5个扇形区域上面写着5 个实数，则转得肯定值小于1的数的概率是 ．11．如图,请你补充一个条件：_________________,使得⊿ABC ∽⊿ADE. 12．用细绳紧紧地捆绑着不同数目的圆木，如下图是它们的正视图（圆的 半径为1），请你仔细视察，试着写出第9个图形中细绳的长度 为 .（结果保存π）二、选择题：（每小题4分，共24分） 13．下列各式正确的是（ ）A ．2054a a a =⋅；B ．53222a a a =+； C ．()94232b a b a =-；D ．34a a a =÷． 14．下列事务中是必定事务的是（ ）A ．父亲的年龄比他亲生儿子的年龄大；B ．下雨天，每个人肯定都打着伞；C ．通过长期的努力，你会成为数学家；D ．你每一分每一秒都保持着甜蜜的笑容． 15．如图，由几个小立方块所搭成的几何体，则这个几何体的主视图是（ ）16．如图，⊙O 是⊿ABC 的外接圆，点D 在⊙O 上，若AB 为直径， BC=AC ，则∠D 的度数为（ ） A ．30°； B ． 40°； C ．45°； D ．60°．21- π2006 6.0 2 （第10题）（第1图） （第2图） （第3图） ……D ．A ．C ． B ． （第4图） A B CD O17．王大爷饭后出去漫步，从家中走 20 分钟到一个离家 900 米的公园，及挚友闲聊10分钟后，然后用15分钟返回家里。

广东华南师范大学附属中学八年级上册压轴题数学模拟试卷含详细答案一、压轴题1．某校七年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究．（1）如图1，在△ABC 中，∠ABC 与∠ACB 的平分线交于点P ，∠A ＝64°，则∠BPC ＝ ；（2）如图2，△ABC 的内角∠ACB 的平分线与△ABC 的外角∠ABD 的平分线交于点E ．其中∠A ＝α，求∠BEC ．（用α表示∠BEC ）； （3）如图3，∠CBM 、∠BCN 为△ABC 的外角，∠CBM 、∠BCN 的平分线交于点Q ，请你写出∠BQC 与∠A 的数量关系，并说明理由；（4）如图4，△ABC 外角∠CBM 、∠BCN 的平分线交于点Q ，∠A=64°，∠CBQ ，∠BCQ 的平分线交于点P ，则∠BPC= ゜，延长BC 至点E ，∠ECQ 的平分线与BP 的延长线相交于点R ，则∠R= ゜．2．已知，在平面直角坐标系中，(42,0)A ，(0,42)B ，C 为AB 的中点，P 是线段AB 上一动点，D 是线段OA 上一点，且PO PD =，DE AB ⊥于E ．（1）求OAB ∠的度数；（2）当点P 运动时，PE 的值是否变化？若变化，说明理由；若不变，请求PE 的值． （3）若45OPD ∠=︒，求点D 的坐标．3．在ABC 中，AB AC =，D 是直线AB 上一点，E 在直线BC 上，且DE DC =． （1）如图1，当D 在AB 上，E 在CB 延长线上时，求证：EDB ACD ∠=∠；（2）如图2，当ABC 为等边三角形时，D 是BA 的延长线上一点，E 在BC 上时，作//EF AC ，求证：BE AD =；（3）在（2）的条件下，ABC ∠的平分线BF 交CD 于点F ，连AF ，过A 点作AH CD ⊥于点H ，当30EDC ∠=︒，6CF =时，求DH 的长度．4．（阅读材科）小明同学发现这样一个规律：两个顶角相等的等腰三角形，如果具有公共的项角的顶点，并把它们的底角顶点连接起来则形成一组全等的三角形，小明把具有这个规律的图形称为“手拉手”图形．如图1，在“手拉手”图形中，小明发现若∠BAC=∠DAE，AB=AC，AD=AE，则△ABD≌△ACE．（材料理解）（1）在图1中证明小明的发现．（深入探究）（2）如图2，△ABC和△AED是等边三角形，连接BD，EC交于点O，连接AO，下列结论：①BD=EC；②∠BOC=60°；③∠AOE=60°；④EO=CO，其中正确的有．(将所有正确的序号填在横线上)．（延伸应用）（3）如图3，AB=BC，∠ABC=∠BDC=60°，试探究∠A与∠C的数量关系．5．问题情景：数学课上，老师布置了这样一道题目，如图1，△ABC是等边三角形，点D 是BC的中点，且满足∠ADE＝60°，DE交等边三角形外角平分线于点E．试探究AD与DE 的数量关系．操作发现：（1）小明同学过点D作DF∥AC交AB于F，通过构造全等三角形经过推理论证就可以解决问题，请您按照小明同学的方法确定AD与DE的数量关系，并进行证明．类比探究：（2）如图2，当点D是线段BC上任意一点(除B、C外)，其他条件不变，试猜想AD 与DE 之间的数量关系，并证明你的结论．拓展应用：（3）当点D 在线段BC 的延长线上，且满足CD ＝BC ，在图3中补全图形，直接判断△ADE 的形状(不要求证明)．6．（1）填空①把一张长方形的纸片按如图①所示的方式折叠，EM ，FM 为折痕，折叠后的C 点落在1B M 或1B M 的延长线上，那么EMF ∠的度数是________；②把一张长方形的纸片按如图②所示的方式折叠，B 点与M 点重合，EM ，FM 为折痕，折叠后的C 点落在1A M 或1A M 的延长线上，那么EMF ∠的度数是_______． （2）解答：①把一张长方形的纸片按如图③所示的方式折叠，EM ，FM 为折痕，折叠后的C 点落在1B M 或1B M 的延长线上左侧，且80EMF ∠=︒，求11C MB ∠的度数； ②把一张长方形的纸片按如图④所示的方式折叠，B 点与M 点重合，EM ，FM 为折痕，折叠后的C 点落在1A M 或1A M 的延长线右侧，且60EMF ∠=︒，求11C MA ∠的度数．（3）探究：把一张四边形的纸片按如图⑤所示的方式折叠，EB ，FB 为折痕，设ABC α∠=︒，EBF β∠=︒，11A BC γ∠=︒，求α，β，γ之间的数量关系．7．学习了三角形全等的判定方法（即“SAS ”、“ASA ”、“AAS ”、“SSS ”）和直角三角形全等的判定方法（即“HL ”）后，我们继续对“两个三角形满足两边的其中一边的对角对应相等”的情形进行研究．（初步思考）我们不妨将问题用符号语言表示为：在△DEF 中，AC ＝DF ，BC ＝EF ，∠B ＝∠E ，然后，对∠B 进行分类，可分为“∠B 是直角、钝角、锐角”三种情况进行探究．（深入探究）第一种情况：当∠B 是直角时，△ABC ≌△DEF ．（1）如图①，在△ABC 和△DEF 中，AC ＝DF ，BC ＝EF ，∠B ＝∠E ＝90°，根据______，可以知道Rt △ABC ≌Rt △DEF ．第二种情况：当∠B 是钝角时，△ABC ≌△DEF ．（2）如图②，在△ABC 和△DEF 中，AC ＝DF ，BC ＝EF ，∠B ＝∠E ，且∠B 、∠E 都是钝角．求证：△ABC ≌△DEF ．第三种情况：当∠B 是锐角时，△ABC 和△DEF 不一定全等．（3）在△ABC 和△DEF 中，AC ＝DF ，BC ＝EF ，∠B ＝∠E ，且∠B 、∠E 都是锐角．请你用直尺在图③中作出△DEF ，使△DEF 和△ABC 不全等，并作简要说明．8．如图，若要判定纸带两条边线a ，b 是否互相平行，我们可以采用将纸条沿AB 折叠的方式来进行探究．（1）如图1，展开后，测得12∠=∠，则可判定a//b ，请写出判定的依据_________； （2）如图2，若要使a//b ，则1∠与2∠应该满足的关系是_________；（3）如图3，纸带两条边线a ，b 互相平行，折叠后的边线b 与a 交于点C ，若将纸带沿11A B （1A ，1B 分别在边线a ，b 上）再次折叠，折叠后的边线b 与a 交于点1C ，AB//11A B ，137BB AC ==，，求出1AC 的长．9．如图，Rt ACB △中，90ACB ∠=︒，AC BC =，E 点为射线CB 上一动点，连结AE ，作AF AE ⊥且AF AE =．（1）如图1，过F 点作FD AC ⊥交AC 于D 点，求证：FD BC =；（2）如图2，连结BF 交AC 于G 点，若3AG =，1CG =，求证：E 点为BC 中点． （3）当E 点在射线CB 上，连结BF 与直线AC 交于G 点，若4BC =，3BE =，则AG CG =______．（直接写出结果） 10．请按照研究问题的步骤依次完成任务．（问题背景）（1）如图1的图形我们把它称为“8字形”， 请说理证明∠A+∠B=∠C+∠D ．（简单应用）（2）如图2，AP 、CP 分别平分∠BAD 、∠BCD ，若∠ABC=20°，∠ADC=26°，求∠P 的度数（可直接使用问题（1）中的结论）（问题探究）（3）如图3，直线AP 平分∠BAD 的外角∠FAD ，CP 平分∠BCD 的外角∠BCE ， 若∠ABC=36°，∠ADC=16°，猜想∠P 的度数为 ；（拓展延伸）（4）在图4中，若设∠C=x ，∠B=y ，∠CAP=13∠CAB ，∠CDP=13∠CDB ，试问∠P 与∠C 、∠B 之间的数量关系为 （用x 、y 表示∠P ） ；（5）在图5中，AP 平分∠BAD ，CP 平分∠BCD 的外角∠BCE ，猜想∠P 与∠B 、D 的关系，直接写出结论 ．11．对x y 、定义一种新运算T ，规定：()()(),2T x y mx ny x y =++（其中mn 、均为非零常数）．例如：()1,133T m n =+．（1）已知()()1,10,0,28T T -==．①求mn 、的值； ②若关于p 的不等式组()()2,244,32T p p T p p a⎧->⎪⎨-≤⎪⎩恰好有3个整数解，求a 的取值范围； （2）当22x y ≠时，()(),,T x y T y x =对任意有理数,x y 都成立，请直接写出mn 、满足的关系式．学习参考：①()a b c ab ac +=+，即单项式乘以多项式就是用单项式去乘多项式的每一项，再把所得的结果相加；②()()a b m n am an bm bn ++=+++，即多项式乘以多项式就是用一个多项式的每一项去乘另一个多项式的每一项，再把所得的结果相加． 12．Rt △ABC 中，∠C =90°，点D 、E 分别是△ABC 边AC 、BC 上的点，点P 是一动点．令∠PDA =∠1，∠PEB =∠2，∠DPE =∠α．（1）若点P 在线段AB 上，如图（1）所示，且∠α=60°，则∠1+∠2= ； （2）若点P 在线段AB 上运动，如图（2）所示，则∠α、∠1、∠2之间的关系为 ； （3）若点P 运动到边AB 的延长线上，如图（3）所示，则∠α、∠1、∠2之间有何关系？猜想并说明理由；（4）若点P 运动到△ABC 形外，如图（4）所示，则∠α、∠1、∠2之间有何关系？猜想并说明理由．13．如图，在ABC 中，3AB AC ==，50B C ∠=∠=，点D 在边BC 上运动（点D 不与点,B C 重合），连接AD ，作50ADE ∠=，DE 交边AC 于点E ．（1）当100BDA ∠=时，EDC ∠= ，DEC ∠=（2）当DC 等于多少时，ABD DCE ≌△△，请说明理由；（3）在点D 的运动过程中，ADE 的形状可以是等腰三角形吗？若可以，请求出BDA∠的度数；若不可以，请说明理由．14．（1）发现：如图1，ABC ∆的内角ABC ∠的平分线和外角ACD ∠的平分线相交于点O 。

广东省广州市华南师范大学附属中学2023~2024学年中考一模数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．2023-的倒数是（ ）A ．12023B ．12023-C ．2023D ．2023-2．奥密克戎是新型冠状病毒，其直径为140纳米（1纳米0.000000001=米）．“140纳米”用科学记数法表示为（ ）A ．111.410-⨯米B ．100.1410-⨯米C ．71.410-⨯米D ．60.1410-⨯米3．下列运算正确的是（ ）A ．()326a a -=-B ．336a a a +=C ．3=D ．62322a a a ÷=【答案】A4．如图，四边形ABCD 内接于O ，如果130BOD ∠=︒，则BAD ∠的度数是（ ）A ．120︒B ．130︒C ．115︒D ．125︒5．在反比例函数y ＝1kx-的每一条曲线上，y 都随着x 的增大而减小，则k 的值可以是（ ）A ．－1B ．1C ．2D ．3【答案】A【分析】利用反比例函数的增减性，y 随x 的增大而减小，则求解不等式1-k>0即可．【详解】∵反比例函数y=1−kx 图象的每一条曲线上，y 随x 的增大而减小，∴1−k>0，解得k<1.故选A.【点睛】此题考查反比例函数的性质，解题关键在于根据其性质求出k 的值.6．若二次函数y ＝x 2﹣2x ﹣m 与x 轴无交点，则一次函数y ＝（m+1）x+m ﹣1的图象不经过（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】A【分析】先根据判别式的意义得到△＝（﹣2）2﹣4（﹣m ）＜0，解得m ＜﹣1，然后根据一次函数的性质进行判断．【详解】∵二次函数y ＝x 2﹣2x ﹣m 与x 轴无交点，∴△＝（﹣2）2﹣4（﹣m ）＜0，解得m ＜﹣1，∵m +1＜0，m ﹣1＜0，∴一次函数y ＝（m +1）x +m ﹣1的图象经过第二、三、四象限，不经过第一象限．故选A ．【点睛】本题考查了抛物线与x 轴的交点：把求二次函数y ＝ax 2+bx +c （a ，b ，c 是常数，a ≠0）与x 轴的交点坐标问题转化为解关于x 的一元二次方程．也考查了一次函数的性质．7．在ABC 中，90C ∠=︒，15AB =，3sin 5B =，则BC 等于（ ）A ．25B ．12C ．9D ．16【点睛】本题考查了解直角三角形，熟练掌握锐角三角函数的定义是解题的关键．8．我国古代数学名著《张邱建算经》中记载：今有清酒一斗直粟十斗，醑酒一斗直粟三斗．今持粟三斛，得酒五斗，问清、醑酒各几何？意思是：现在一斗清酒价值10斗谷子，一斗醑酒价值3斗谷子，现在拿30斗谷子，共换了5斗酒，问清、醑酒各几斗？如果设清酒x 斗，那么可列方程为（ ）A ．()103530x x +-=B ．()310530x x +-=C ．305103x x -+=D ．305310x x-+=【答案】A【分析】本题考查了一元一次方程的应用，找出数量关系是解题关键．设清酒x 斗，则醑酒()5x -斗，根据题意正确列方程即可．【详解】解：设清酒x 斗，则醑酒()5x -斗，由题意可得：()103530x x +-=，故选：A ．9．如图，在平行四边形ABCD 中，∠ABC 的角平分线交AD 于点E ，∠BCD 的角平分线交AD 于点F ，若AB =7，BC =10，则EF 的长为（ ）A ．4B ．3C ．6D ．5【答案】A【分析】根据平行四边形的性质可知∠DFC =∠FCB ，又因为CF 平分∠BCD ，所以∠DCF =∠FCB ，则∠DFC =∠DCF ，则DF =DC ，同理可证AE =AB ，那么EF 就可表示为AE +FD -BC =2AB -BC ，继而可得出答案．【详解】解：∵平行四边形ABCD ，∴AD ∥BC ，∴∠DFC =∠FCB ，又CF 平分∠BCD ，∴∠DCF =∠FCB ，∴∠DFC =∠DCF ，∴DF =DC ，同理可证：AE =AB ，∵AB =7，AD =BC =10，∴EF =AE +FD -AD =2AB -BC =4．故选：A ．【点睛】本题主要考查了平行四边形的性质，在平行四边形中，当出现角平分线时，一般可利用等腰三角形的性质解题，难度不大，关键是解题技巧的掌握．10．如图，在平面直角坐标系中，点A 、B 在函数(0,0)k y k x x=>>的图象上，x 过点A 作x 轴的垂线，与函数(0)k y x x=->的图象交于点C ，连结BC 交x 轴于点D ．若点A 的横坐标为1，3BC BD =，则点B 的横坐标为（ ）A ．32B ．2C ．52D ．3【答案】B【分析】首先设出A 的坐标，根据题意得出C 的坐标，表示出CE 的长度，过点B 作BF 垂直x 轴，证明CED BFD V :V ，由题目条件3BC BD =得出相似比，代换出点B 的纵坐标，二、填空题11．计算：13tan30︒= ．12．分式方程123x x =+的解为 ．13．已知点2()1,M -和点N 都在抛物线22y x x c =-+上，如果MN x ∥轴，那么点N 的坐标为 ．【答案】(3,2)【分析】将2()1,M -代入抛物线22y x x c =-+中，可得1c =-，即抛物线解析式为：221y x x =--，根据MN x ∥轴，可得2N M y y ==，令2y =，解方程即可求解．【详解】将2()1,M -代入抛物线22y x x c =-+中，可得：()()22121c =--⨯-+，解得：1c =-，即抛物线解析式为：221y x x =--，∵MN x ∥轴，2()1,M -，∴2N M y y ==，当2y =时，2212x x --=，解得：3x =，或者=1x -，即(3,2)M ，故答案为：(3,2)．【点睛】本题考查了二次函数的图象与性质，解一元二次方程的知识，根据MN x ∥轴，得出2N M y y ==，是解答本题的关键．14．如图，直线AB 切O 于点A ，BO 交O 于点C ，点D 是 CmA 上异于点C 、A 的一点，若32ABO ∠=︒，则ADC ∠的度数是 ．周角定理是解题的关键．15．若关于x 的一元二次方程210(0)4ax x a --=≠有两个不相等的实数根，则点(1, 3 )P a a +--在第 象限．16．如图，在Rt ABC △中，斜边10AB =，4sin 5A =，点P 为边AB 上一动点（不与A ，B 重合），PQ 平分CPB ∠交边BC 于点Q ，QM AB ⊥于M ，⊥QN CP 于N ．（1）当AP CP =时，线段CQ 的长是 ．（2）当CP AB ⊥时，线段CQ 的长是．三、解答题17．解不等式组：3(2)41213x x x x --≥⎧⎪+⎨-<⎪．18．如图，在ABCD Y 中，点E ，F 分别在AD ，BC 上，且AE CF =．求证：AF CE =．【答案】见解析【分析】先得到AE ∥FC ，而AE =CF ，所以AFCE 是平行四边形，即可证明．【详解】解：证明：∵四边形ABCD 是平行四边形，∴AE ∥CF ，又∵AE =CF ，∴四边形AFCE 是平行四边形，∴AF =CE ．【点睛】本题考查了平行四边形的判定与性质，熟练掌握性质定理和判定定理是解题的关键．平行四边形的五种判定方法与平行四边形的性质相呼应，每种方法都对应着一种性质，在应用时应注意它们的区别与联系．19．已知：22222m n mn n P m m m mn ⎛⎫-+=÷+ ⎪-⎝⎭(1)化简P ；(2)若函数3m n y x +=为反比例函数，求P 的值．题关键．20．实施新课程改革后，学生的自主学习、合作交流能力有很大提高，张老师为了了解所教班级学生自主学习、合作交流的具体情况，对本班部分学生进行了为期半个月的跟踪调查，并将调查结果分成四类，A：特别好；B：好；C：一般；D：较差；并将调查结果绘制成以下两幅不完整的统计图，请你根据统计图解答下列问题：（1）本次调查中C类女生有______名，D类男生有______名；将上面的条形统计图补充完整；（2）计算扇形统计图中D所占的圆心角是______；（3）为了共同进步，张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习，请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率．故答案为：2，1；（2）扇形统计图中D 所占的圆心角是360°×220=36°，故答案为：36°；（3）画树状图得：∵共有6种等可能的结果，所选两位同学恰好是一位男同学和一位女同学的有∴所选两位同学恰好是一位男同学和一位女同学的概率是【点睛】本题考查了列表法或树状图法求概率、树状图分析求解概率，结合条形统计图与扇形统计图均已知的量求出总人数是解题关键．21．如图，一次函数y kx b =+与反比例函数y =mx的图象相交于()2,3A ，()3,B n -两点．过点B 作BC x ⊥轴，垂足为C ，(1)求一次函数与反比例函数的解析式；(2)根据所给条件，请直接写出不等式kx b +>mx的解集；(3)一次函数y kx b =+的图像上是否存在一点P ，使得求2BCP ABC S S =△△．若存在，求出P 点坐标，若不存在说明理由．把0y =代入1y x =+可得：x =-即()1,0D -；()3,2B -- ，BC x ⊥轴，垂足为∴()3,0C -∴2CD =，2BC =,22．如图是一个山坡的纵向剖面图，坡面DE 的延长线交地面AC 于点B ，点E 恰好在BD 的中点处，60CBD ∠=︒，坡面AE 的坡角为45°，山坡顶点D 与水平线AC 的距离，即CD的长为．(1)求BE 的长度；(2)求AB 的长度．（结果保留根号）在FEB 中，500BE =，∴cos BF BE EBF =⨯∠=在Rt EFA △中，tan A ∠=23．如图所示，在ABC 中，AB AC ==30B ∠=︒，点O 为边BC 上一点，以O 为圆心的圆经过点A ，B ．(1)求作圆O （尺规作图，保留作图痕迹，不写作法）；(2)求证：AC 是O 的切线；(3)若点P 为圆O 上一点，且弧PA =弧PB ，连接PC ，求线段PC 的长．（2）证明：连接OA ，OA OB = ，30OAB B ∴∠=∠=︒，AB AC = ，'⊥于点E，作P E BC'⊥，OP AB根据垂径定理，得AF BF==1AB=3，224．已知点()1,0A 是抛物线2y ax bx m =++（,,a b m 为常数，0,0a m ≠<）与x 轴的一个交点．（1）当1,3a m ==-时，求该抛物线的顶点坐标；（2）若抛物线与x 轴的另一个交点为(),0M m ，与y 轴的交点为C ，过点C 作直线l 平行于x 轴，E 是直线l 上的动点，F 是y 轴上的动点，EF =①当点E 落在抛物线上（不与点C 重合），且AE EF =时，求点F 的坐标；②取EF 的中点N ，当m 为何值时，MN25．如图①，在四边形ABCD 中，AB BC AD ==，90ABC ∠=︒，60BAD ∠=︒．(1)求ACD ∠的度数；(2)如图②，F 为线段CD 的中点，连接BF ，求证：2BF CD =；(3)如图③，若125OB AB ==，线段BC 上有一动点M ，连接OM ，将OBM 沿OM 所在直线翻折至OPM 的位置，P 为B 的对应点，连接PA ，PC ，请直接写出4PC PA +的最小值．ABD ∴ 是等边三角形，60ABD ∴∠=︒，BD AB =，AB BC = ，90ABC ∠=︒，906030DBC ∴∠=︒-︒=︒，ACB ∠=(1180302BCD BDC ∴∠=∠=⨯︒-︒7545ACD BCD BCA ∴∠=∠-∠=︒-︒=（2）证明：如图2中，连接BD ，延长 BF CD ∴⊥，ED EC CD ∴==，EDC ∴ 是等边三角形，60ADB CDE ∴∠=∠=︒，125OB AB == ，10AB BC ∴==，8OA =，2OB OP == ，∴点P 在 BP上运动，设CK 交圆弧于点2OP = ，12OK =，8AO =，。

九年级数学练习题(综合练习三)班级 座号 姓名 成绩一、填空题：（每小题3分，共36分） 1．－2的相反数是 ．2．分解因式：=-x x 2． 3．函数1-=x y 中，自变量x 的取值范围是 ．4．爱需要从小事做起，如果人人都向“希望工程”捐款1毛钱，全中国的捐款数额将会超过130000000元，这些钱将使许多失学儿童重返学校，用科学记数表示这一数据为 ．5．不等式组：⎪⎩⎪⎨⎧<-≤-1221x x 的解集为 ．6．一个多边形的内角和与它的外角和相等，则这个多边形的边数是 ． 7．写出一个既是轴对称图形，又是中心对称图形的图形： ． 8．抛物线()3122+-=x y 的顶点坐标是.9．从10000名初三学生中，随机地抽取100名学生，测得他们所穿鞋的鞋号（单位：公分），则这个样本数据的平均数、中位数、众数、方差四个指标中，鞋厂最感兴趣的指标是 .10．如右图的转盘中，图中面积大小相同的5个扇形区域上面写着5 个实数，则转得绝对值小于1的数的概率是 ．11．如图,请你补充一个条件：_________________,使得⊿ABC ∽⊿ADE. 12．用细绳紧紧地捆绑着不同数目的圆木，如下图是它们的正视图（圆的 半径为1），请你认真观察，试着写出第9个图形中细绳的长度 为 .（结果保留π）二、选择题：（每小题4分，共24分） 13．下列各式正确的是（ ）A ．2054a a a =⋅；B ．53222a a a =+； C ．()94232b a b a =-；D ．34a a a =÷． 14．下列事件中是必然事件的是（ ）A ．父亲的年龄比他亲生儿子的年龄大；B ．下雨天，每个人一定都打着伞；C ．通过长期的努力，你会成为数学家；D ．你每一分每一秒都保持着甜蜜的笑容． 15．如图，由几个小立方块所搭成的几何体，则这个几何体的主视图是（ ）16．如图，⊙O 是⊿ABC 的外接圆，点D 在⊙O 上，若AB 为直径， 21-π20066.02（第10题） （第1图） （第2图） （第3图） ……D ． A ．C ． B ． （第4图）A B C D OBC=AC ，则∠D 的度数为（ ）A ．30°；B ． 40°；C ．45°；D ．60°．17．王大爷饭后出去散步，从家中走 20 分钟到一个离家 900 米的公园，与朋友聊天10分钟后，然后用15分钟返回家里。