福利经济学第一定理:数学证明
- 格式:docx
- 大小:264.31 KB
- 文档页数:7


Stiglitz: “社会主义向何处去” (“Whither Socialism?”,,MIT Press, 1994)第三章福利经济学第一定理批判在第三和第四章中,我们将回到福利经济学基本定理的讨论上。
在本章中,我将指出福利经济学第一定理是有缺陷的。
该定理认为竞争性经济是有效率的。
与该定理描述的恰恰相反,竞争性经济几乎都是无效率的(下文将作详细论述)。
下一章对福利经济学第二定理做了类似的批判性分析。
在这两章中,我将着重讨论由完全信息和完备市场体系的假设而引发的问题。
其他问题将在以后的章节中进行讨论,例如由缺乏内生性技术变动的假设而引发的问题。
福利经济学第一定理指出,每一个竞争性经济都具有帕累托效率。
这是对亚当·斯密看不见的手的假说提出的一种现代说法:人们总是需要同胞的帮助,然而一个人只想从别人那里得到恩惠却是徒劳的。
如果一个人可以将自己的利益与其他人的私利联系起来,并告诉他人出于他们自身利益的考虑,他们应为此人做些什么 那他要达到目的将会容易得多。
……我们并不是靠屠夫,酿酒师和面包师的恩惠吃饭,而是他们考虑到自身的利益,这些人才会给我们食物。
我们告诫自己,他们只有私利而没有仁慈,不要和他们谈论我们所需要的,而只谈他们的私利。
斯密继续描述私利是如何导致社会商品的:一个人所盘算的只是自己的利益,在这种场合,像在其他许多场合一样,他会受一只看不见的手指导,进而导致了一种非他本意的结局。
对于社会来说,这种情况并不总是有害。
他追逐自己的利益,往往使他能比在真正出于其本意的情况下更有效地促进社会利益的实现。
…福利经济学第一定理给人们对市场经济的信心提供了理论基础。
像其他定理一样,它的结论则取决于假设条件的有效性。
然而,进一步研究它则会发现,该定理与现代工业化经济的实际情况并不吻合。
竞争性市场效率的格林沃德一斯蒂格利茨定理⑵留意作者所强调的假设条件,并标注“条件A.1…… A.10”,同时注意作者有意或无意隐藏的假设条件都是非常有趣的事。
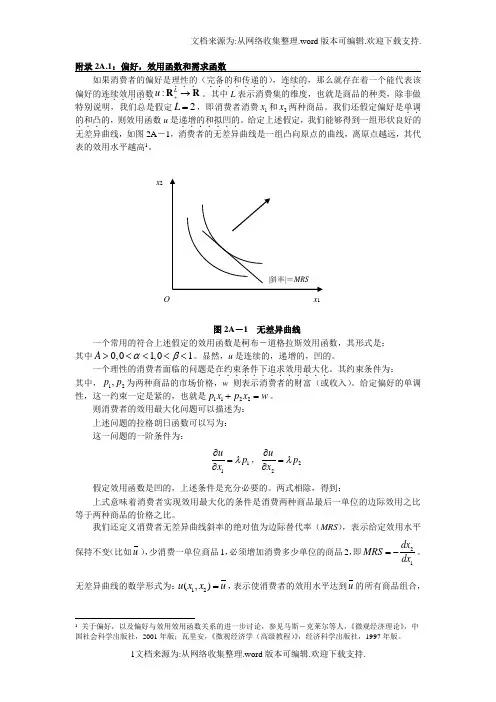
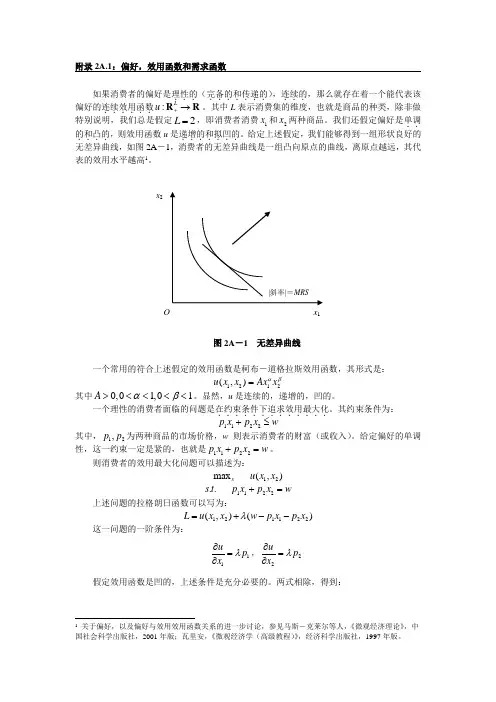
附录2A.1:偏好,效用函数和需求函数如果消费者的偏好是理性的...(完备的和传递的.......),连续的...,那么就存在着一个能代表该偏好的连续效用函数......:L u +→R R 。
其中L 表示消费集的维度,也就是商品的种类,除非做特别说明,我们总是假定2L =,即消费者消费1x 和2x 两种商品。
我们还假定偏好是单调..的和凸的....,则效用函数u 是递增的和拟凹的.......。
给定上述假定,我们能够得到一组形状良好的无差异曲线,如图2A -1,消费者的无差异曲线是一组凸向原点的曲线,离原点越远,其代表的效用水平越高1。
图2A -1 无差异曲线 一个常用的符合上述假定的效用函数是柯布-道格拉斯效用函数,其形式是:其中0,01,01A αβ><<<<。
显然,u 是连续的,递增的,凹的。
一个理性的消费者面临的问题是在约束条件下追求........效用最大化.....。
其约束条件为: 其中,12,p p 为两种商品的市场价格,w 则表示消费者的财富(或收入)。
给定偏好的单调性,这一约束一定是紧的,也就是1122p x p x w +=。
则消费者的效用最大化问题可以描述为:上述问题的拉格朗日函数可以写为:这一问题的一阶条件为:11u p x λ∂=∂,22u p x λ∂=∂ 假定效用函数是凹的,上述条件是充分必要的。
两式相除,得到:上式意味着消费者实现效用最大化的条件是消费两种商品最后一单位的边际效用之比等于两种商品的价格之比。
我们还定义消费者无差异曲线斜率的绝对值为边际替代率(MRS ),表示给定效用水平保持不变(比如u ),少消费一单位商品1,必须增加消费多少单位的商品2,即21dx MRS dx =-。
无差异曲线的数学形式为:12(,)u x x u =,表示使消费者的效用水平达到u 的所有商品组合,1 关于偏好,以及偏好与效用效用函数关系的进一步讨论,参见马斯-克莱尔等人,《微观经济理论》,中国社会科学出版社,2001年版;瓦里安,《微观经济学(高级教程)》,经济科学出版社,1997年版。

福利经济学第一二定理一、福利经济学第一定理1. 定义- 福利经济学第一定理是指在完全竞争的市场条件下,市场机制所导致的资源配置是帕累托最优的。
这意味着在这种理想的市场环境中,任何重新配置资源的方式都无法在不使其他人的状况变坏的情况下使至少一个人的状况变好。
2. 假设条件- 市场是完全竞争的。
完全竞争市场有许多买者和卖者,产品是同质的,资源可以自由流动,并且市场信息是完全的。
例如,在农产品市场上,有众多的小农户(卖者)和消费者(买者),小麦等农产品基本是同质的,农民可以根据价格自由决定种植面积(资源流动),而且市场价格信息对所有人都是公开透明的。
- 不存在外部性。
即一个人的经济活动不会对其他人的福利产生未在市场交易中反映的影响。
一家工厂在生产过程中如果没有污染环境(不存在负外部性),也没有因为其存在而给周边带来额外的好处(不存在正外部性)。
- 不存在公共物品。
公共物品具有非排他性和非竞争性,与完全竞争市场的假设不符。
例如国防是公共物品,一旦国家提供了国防保护,就无法排除任何一个公民享受这种保护,而且一个公民享受国防保护并不影响其他公民享受同样的保护。
完全竞争市场假设所涉及的产品都是私人物品。
3. 证明思路(简单示意)- 在完全竞争市场中,消费者追求效用最大化,生产者追求利润最大化。
对于消费者来说,他们根据商品的价格来调整自己的消费组合,使得每一种商品的边际替代率等于其价格之比。
对于生产者来说,他们根据生产要素的价格来调整生产组合,使得边际技术替代率等于要素价格之比。
由于价格机制的作用,在市场均衡时,所有消费者的边际替代率相等,所有生产者的边际技术替代率相等,并且消费者的边际替代率等于生产者的边际转换率,这就满足了帕累托最优的三个条件(交换的帕累托最优、生产的帕累托最优和生产与交换的帕累托最优),从而证明了在完全竞争市场下资源配置是帕累托最优的。
4. 意义- 从理论上肯定了市场机制的有效性。
它表明在理想的市场条件下,不需要政府的干预,市场自身就能实现资源的最优配置。
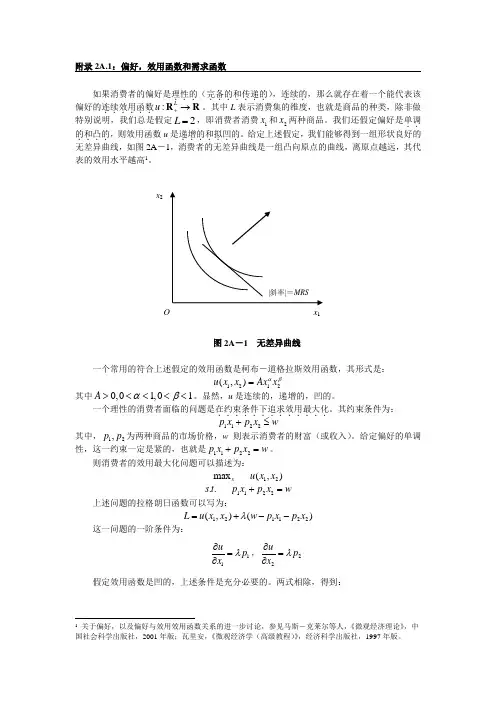
附录2A.1:偏好,效用函数和需求函数如果消费者的偏好是理性的...(完备的和传递的.......),连续的...,那么就存在着一个能代表该偏好的连续效用函数......:Lu +→R R 。
其中L 表示消费集的维度,也就是商品的种类,除非做特别说明,我们总是假定2L =,即消费者消费1x 和2x 两种商品。
我们还假定偏好是单调..的和凸的....,则效用函数u 是递增的和拟凹的.......。
给定上述假定,我们能够得到一组形状良好的无差异曲线,如图2A -1,消费者的无差异曲线是一组凸向原点的曲线,离原点越远,其代表的效用水平越高1。
图2A -1 无差异曲线一个常用的符合上述假定的效用函数是柯布-道格拉斯效用函数,其形式是:1212(,)u x x Ax x αβ=其中0,01,01A αβ><<<<。
显然,u 是连续的,递增的,凹的。
一个理性的消费者面临的问题是在约束条件下追求效用最大化.............。
其约束条件为:1122p x p x w +≤其中,12,p p 为两种商品的市场价格,w 则表示消费者的财富(或收入)。
给定偏好的单调性,这一约束一定是紧的,也就是1122p x p x w +=。
则消费者的效用最大化问题可以描述为: 12max (,)x u x x1122..s t p x p x w +=上述问题的拉格朗日函数可以写为:121122(,)()L u x x w p x p x λ=+--这一问题的一阶条件为:11u p x λ∂=∂,22up x λ∂=∂ 假定效用函数是凹的,上述条件是充分必要的。
两式相除,得到:1关于偏好,以及偏好与效用效用函数关系的进一步讨论,参见马斯-克莱尔等人,《微观经济理论》,中国社会科学出版社,2001年版;瓦里安,《微观经济学(高级教程)》,经济科学出版社,1997年版。
Ox 1x21212u up p x x ∂∂=∂∂ 上式意味着消费者实现效用最大化的条件是消费两种商品最后一单位的边际效用之比等于两种商品的价格之比。

名词解释福利经济学第一定理
福利经济学第一定理是指在完全竞争市场中,通过个人追求自身利益最大化和价格的调整所实现的均衡,即完全竞争均衡,在经济上是帕累托最优配置。
也就是说,如果所有的个人和企业都是以自我利益为中心的价格接受者,则竞争性均衡具有帕累托最优效率。
福利经济学第一定理隐含了以下几层意思:第一,竞争均衡的结果是帕累托有效的,但它与分配无关,利润最大化只保证效率,不保证公平;第二,竞争均衡是帕累托有效均衡只有在竞争均衡实际存在时才有效,因此排除了较大的规模收益递增的区域;第三,福利经济学第一定理暗含假定了任何一家厂商的选择并不影响它们的生产可能性边界,也就是说不存在生产的外部效应和消费的外部效应。
福利经济学第一定理中任何一个竞争均衡的分配结果都是帕累托最优的,即达到了没有人可以在不伤害其他人的前提下改善自身福利的状态。
对许多人来说,这一定理是自由竞争的胜利。
但是,自由竞争还不能与帕累托最优划等号。
福利经济学第二定理恰恰表明了这一点。
这一定理说的是,如果可以对行动个体的初始禀赋进行适当的再分配,则任何一个帕累托最优的社会分配都可以通过自由竞争达到。
这里的前提条件是相当惊人的,因为它等于是说,要达到某个特定的帕累托社会分配,以财富再分配为目标的社会革命是必要的,由于这一原因,经济学家更看重福利经济学第一定理。

附录2A.1:偏好,效用函数和需求函数如果消费者的偏好是理性的...(完备的和传递的.......),连续的...,那么就存在着一个能代表该偏好的连续效用函数......:Lu +→R R 。
其中L 表示消费集的维度,也就是商品的种类,除非做特别说明,我们总是假定2L =,即消费者消费1x 和2x 两种商品。
我们还假定偏好是单调..的和凸的....,则效用函数u 是递增的和拟凹的.......。
给定上述假定,我们能够得到一组形状良好的无差异曲线,如图2A -1,消费者的无差异曲线是一组凸向原点的曲线,离原点越远,其代表的效用水平越高1。
图2A -1 无差异曲线一个常用的符合上述假定的效用函数是柯布-道格拉斯效用函数,其形式是:1212(,)u x x Ax x αβ=其中0,01,01A αβ><<<<。
显然,u 是连续的,递增的,凹的。
一个理性的消费者面临的问题是在约束条件下追求效用最大化.............。
其约束条件为:1122p x p x w +≤其中,12,p p 为两种商品的市场价格,w 则表示消费者的财富(或收入)。
给定偏好的单调性,这一约束一定是紧的,也就是1122p x p x w +=。
则消费者的效用最大化问题可以描述为: 12max (,)x u x x1122..s t p x p x w +=上述问题的拉格朗日函数可以写为:121122(,)()L u x x w p x p x λ=+--这一问题的一阶条件为:11u p x λ∂=∂,22up x λ∂=∂ 假定效用函数是凹的,上述条件是充分必要的。
两式相除,得到:1关于偏好,以及偏好与效用效用函数关系的进一步讨论,参见马斯-克莱尔等人,《微观经济理论》,中国社会科学出版社,2001年版;瓦里安,《微观经济学(高级教程)》,经济科学出版社,1997年版。
Ox 1x21212u up p x x ∂∂=∂∂ 上式意味着消费者实现效用最大化的条件是消费两种商品最后一单位的边际效用之比等于两种商品的价格之比。

福利经济学第一基本定理的反例本文从网络收集而来,上传到平台为了帮到更多的人,如果您需要使用本文档,请点击下载按钮下载本文档(有偿下载),另外祝您生活愉快,工作顺利,万事如意!二百多年前,亚当·斯密用“看不见的手”来形容一个经济中许多当事人各自独立地追求自我利益的行为非但没有造成混沌,反而实际产生了一个社会最优状态。
建立在数学基础上的福利经济学第一、第二基本定理是这一深刻思想的现代形式,但这首先依赖于均衡的存在。
本文以数理模型说明福利经济学第一基本定理不成立,这也意味着阿罗-德布鲁一般均衡模型(Arrow-DebreuModel)不完善。
一以下的经典数学结果依照阿罗、德布鲁五十年代的定义和证明,本文只对表述方式作了一定的修改。
商品空间R是l维Euclid空间。
经济e=[ Xi , ≥i , Yj ,w]i=1,2,3.....,n;j=1,2,3.....m是消费者i的消费集;是生产者j的生产集;≥i 是消费者i的偏好关系;w是经济的总禀赋。
满足:(1)Xi凸,闭且下有界;(2)≥i连续,凸;(3)(4)凸,闭;(5)(6)。
可行状态(,)满足:且。
帕累托效率(最优)状态()是可行状态,且不存在可行状态()满足有,并有。
瓦尔拉斯均衡(,p*)是私有制经济下的一个均衡,其中消费者i以股份θij拥有企业j,满足:(A)在i的预算集{}上使偏好≥i极大,其中。
(B)使j的利润极大;(C),是i的初始禀赋。
Arrow-Debreu一般均衡存在性定理:上述经济(条件(1)~(6)成立)中,如果任何一个消费者都没有充分满足的消费束,且在其消费集内部都有一个初始禀赋,那么上述定义的瓦尔拉斯均衡存在。
福利经济学第一基本定理:上述竞争均衡配置是帕累托效率的。
下面是一个说明福利经济学第一基本定理错误的模型。
[模型S]生产–交换经济e。
商品:x,y,z,v,w。
当事人:消费者A,B;厂商X,Y。
偏好:A的偏好函数B的偏好函数。
文章标题:深度剖析福利经济学第一定理和第二定理一、引言在经济学领域中,福利经济学是一个重要而复杂的概念,其中第一定理和第二定理更是福利经济学的核心内容之一。
在本文中,我们将从浅入深地探讨福利经济学第一定理和第二定理,以期让读者更深入地理解这一重要的经济学原理。
二、福利经济学第一定理福利经济学第一定理是指,在竞争性市场条件下,资源的有效配置达到了帕累托最优状态,这表明资源分配已经达到了一种不能再通过重新分配实现某个人的福利水平提高而不损害其他人的福利水平的状态。
简单来说,就是市场的自发机制会使得资源配置达到最优状态,而且在这种状态下,任何人的福利都不能再通过简单的转移获得利益。
这一定理强调了市场的有效性和竞争的重要性,从而揭示了市场经济的优越性。
在现实生活中,我们可以通过大量的案例来说明福利经济学第一定理的应用。
某个市场上的商品价格随着供求关系不断变化,最终会使得市场上的资源得到了有效的配置,并实现了最优状态。
这一定理对于我们理解市场经济和资源配置具有重要意义。
三、福利经济学第二定理福利经济学第二定理是指,在存在市场摩擦或者外部扰动的情况下,通过适当的再分配,可以使得任何帕累托改进的社会选择都能够通过合适的转移支付来实现。
简单来说,就是在市场条件不完全有效的情况下,可以通过再分配来实现资源配置的最优化。
这一定理强调了政府在市场调节中的重要作用,从而揭示了市场经济的不完美性。
在现实生活中,我们可以通过一些政府的再分配政策来说明福利经济学第二定理的应用。
政府通过税收政策和社会保障制度来实现资源再分配,从而实现了资源配置的最优状态。
这一定理对于我们理解政府在市场经济中的作用具有重要意义。
四、个人观点和理解从我的个人观点和理解来看,福利经济学第一定理和第二定理在揭示了市场经济的优越性和不完美性的也为我们提供了重要的理论基础和政策指导。
在实践中,我们需要通过不断的市场改革和政策创新,来实现资源的有效配置和再分配,使得社会福利能够得到最大化的提升。
福利经济学第一定理各位同学好,有了前面的埃奇沃斯盒状图以及相关其他的一些准备了之后,我们这次课给大家讲福利经济学第一定理。
那么这次课的内容我们给大家讲三个内容,一个是生产可能性曲线,一个是组合效率,还有一个是福利经济学第一定律。
首先我们再回顾一下,生产效率的横轴纵轴分别是投入K跟L,两个顶端分别是两种计划生产的商品x和y,通过两种投入来讨论生产两种商品的效率,可以看到(埃奇沃斯盒状图内)一条契约曲线,契约曲线上的所有点都是等产量曲线相切的点,这些点上的边际技术替代率相等。
那么,每种相切的等产量线可代表一组X跟Y的产量,我们把这个埃奇沃斯盒状图放在左边,每一组相切的等产量线分别代表一种X和Y的产量,它可以形成以生产物品X跟Y为纵横坐标的一个二维空间坐标点。
左图的R1、R2点,它们分别表示什么呢?R1点的X产量要比R2点的X产量要低,而R2点的Y产量要比x产量要低?所以,它们之间是个负相关的关系,即右边的这个图,称之为生产的可能性曲线,也就是说左图契约曲线上面所有的点都是帕累托最优点,意味着增加x产量的唯一途径是减少Y的产量。
在这种情况下,它的斜率显然是负的。
生产的可能性曲线是指固定的投入之下,给定某一种物品的产量,能够生产的另外一种产品的最大产量;如果要增加另外一种产品的产量,只能减少前一种产品的产量。
所以,生产可能性曲线的所有的点也是帕累托最优点,而在可能性曲线内的点不是帕累托最优点,比如说F,在不减少X产量的情况下可以增加Y的产量,也可以不减少Y的产量而增加X的产量。
在这个扇形区域内,我们有无穷多种进行帕累托改进的方式,这跟在埃奇沃斯盒状图里面讨论的是一样的。
扇形区域的内部点不是帕累托最优点,而在生产可能性曲线上的所有的点都是帕累托最优点。
生产可能性曲线上的任意点的斜率,称之为边际转换率,经济学意义是指放弃某一种商品的生产而去生产另外一种商品的代价。
另外一个有趣的一个结论就是由于边际产量递减,生产可能性曲线是凹向原点的。
附录2A.1 :偏好,效用函数和需求函数如果消费者的偏好是理性的.(完备的和传递的),连续的,那么就存在着一个能代表该偏好的连续.效用函.数.u:R L> R。
其中L表示消费集的维度,也就是商品的种类,除非做特别说明,我们总是假定L = 2,即消费者消费x-i和x2两种商品。
我们还假定偏好是单调. 的和凸的,则效用函数u是递增的和拟凹的。
给定上述假定,我们能够得到一组形状良好的无差异曲线,如图2A —1,消费者的无差异曲线是一组凸向原点的曲线,离原点越远,其代表的效用水平越高I O图2A —1无差异曲线一个常用的符合上述假定的效用函数是柯布-道格拉斯效用函数,其形式是:u(%,x2) = A^x2其中A・0,0 I—::1,0 :::'■ :::1。
显然,u是连续的,递增的,凹的。
一个理性的消费者面临的问题是在约束条件下追求效用最大化..。
其约束条件为:p1x1 p2x2三W其中,P1, P2为两种商品的市场价格,w则表示消费者的财富(或收入)。
给定偏好的单调性,这一约束一定是紧的,也就是p1x1 p2x2 w。
则消费者的效用最大化问题可以描述为:max x u(x1, x2)s.t p)x1 p2x2 =w上述问题的拉格朗日函数可以写为:L =u(^,x2)' (w- 口為-p2x2)这一问题的一阶条件为:r\ l、u :uP1,P2:x x2假定效用函数是凹的,上述条件是充分必要的。
两式相除,得到:I关于偏好,以及偏好与效用效用函数关系的进一步讨论,参见马斯-克莱尔等人,《微观经济理论》,中国社会科学出版社,2001年版;瓦里安,《微观经济学(高级教程)》,经济科学出版社,1997年版。
上式意味着消费者实现效用最大化的条件是消费两种商品最后一单位的边际效用之比 等于两种商品的价格之比。
我们还定义消费者无差异曲线斜率的绝对值为边际替代率(MRS ),表示给定效用水平保持不变(比如U ),少消费一单位商品1,必须增加消费多少单位的商品2,即MRS =-無无差异曲线的数学形式为:u (x 「x 2) = u ,表示使消费者的效用水平达到 U 的所有商品组合, 两位全微分,得到 —dx^ — dx^dU =0,这样我们就得到,-坐二,U 。
福利经济学两个基本定理:瓦尔拉斯均衡与帕雷托有效之间的关系一、福利经济学的第一定理:瓦尔拉斯均衡配置一定是帕雷托有效的。
定义:瓦尔拉斯均衡配置WEAs :对于一些初始禀赋为e 的经济而言,如果下列式子成立,那么,P*是一个瓦尔拉斯均衡:))e P ,(P X ),...,e P ,(P (X )X(P I **I 1**1*这里第i 个分量(代表第i 个消费者)给出价格为p*时消费者I 所需求并获得的n 维商品向量。
这时x(p*),被称为一个瓦尔拉斯均衡配置WEA 。
瓦尔拉斯均衡是一个n 个价格组成的向量p*,该价格向量使各个市场供求都相等;瓦尔拉斯均衡配置是一个需求矩阵,它指的是当价格使各个市场都实现均衡时每个消费者对于n 种商品所需求的并获得的商品数量。
引理:瓦尔拉斯均衡配置一定是可行的配置:F(e)X(P*)∈ 引理:设u i 在n +R 上是严格递增的,消费者i 的需求在0≥p 是界定良好并等于i X ˆ,并且n i +∈R X ,(1)ii i i i u ifu X P PX XX i ˆ)ˆ)((>⇒> (2)i i i i i u ifu X P PX X X i ˆ)ˆ)((≥⇒≥在WEAs 中,每个消费者所接受的消费束(无差异曲线的交点)是在瓦尔拉斯均衡价格上消费者预算集中最受偏好的消费束。
在WEAs 中如果还存在其他既可行又更受偏好的消费束,那它一定是消费不起的。
对应于不同的瓦尔拉斯均衡价格,可能()有不同的瓦尔拉均衡配置,这些配置形成WEAs:定义:W(e)表示对于初始禀赋为e 的任何经济的瓦尔拉斯均衡配置集WEAs 集。
定理核与竞争性经济的均衡考虑一个交换经济I i i i ∈),(e u ,如果每一个消费者的效用函数u i在上是严格递增的,那么,每一个瓦尔拉斯均衡配置都处于核内,即)()(e e C W ⊂。
反证法:设对于W(e)内的一个瓦尔拉斯均衡配置X(P*),假设)(e X(P*)C ∉。
福利经济学第一定理的证明
Step 1: 一般均衡是可行的
用(,)和(,)来表示一般均衡的配置
一般均衡配置一定是可行(可以实现:达到均衡时)
Step 2: 一般均衡是帕累托有效的(反证法)
假设另外存在一个帕累托较优配置(X
a,Y a)和(X b,Y b),
优于,)(,)
这样我们有(X
a,Y a)>(,)(X b,Y b)>(,)
假设初始禀赋是(,)和(,)
根据供求平衡有和
这是不可能的? 根据显示弱偏好原理
在均衡价格(,)下选择了(,)而非(X
a,Y a),
说明A在价格(,)下买不起(X
a,Y a),
所以有:
同理对B有:
矛盾!所以假设另外存在一个帕累托较优的配置是不成立的。
福利经济学第一定理保证了竞争市场可以使贸易利益达到最大,即一组竞争市场所达到的均衡分配必定是帕累托有效配置。
在完全竞争条件下,市场竞争能够通过价格有效率的协调经济活动,从而配置有限的稀缺资源。
福利经济学第一定理的政策启示
•政府为了实现公平干预市场定价有可能导致市场低效率;
•政府为了实现公平对交易者的禀赋进行征税并不能改变
帕累托有效率配置。
始于任何初始商品禀赋的交易都会导
致一种帕累托有效率配置。
不管一个人如何重新分配禀赋,
有市场力量决定的均衡配置依然是帕累托有效率配置。
附录2A.1:偏好,效用函数和需求函数如果消费者的偏好是理性的...(完备的和传递的.......),连续的...,那么就存在着一个能代表该偏好的连续效用函数......:Lu +→R R 。
其中L 表示消费集的维度,也就是商品的种类,除非做特别说明,我们总是假定2L =,即消费者消费1x 和2x 两种商品。
我们还假定偏好是单调..的和凸的....,则效用函数u 是递增的和拟凹的.......。
给定上述假定,我们能够得到一组形状良好的无差异曲线,如图2A -1,消费者的无差异曲线是一组凸向原点的曲线,离原点越远,其代表的效用水平越高1。
图2A -1 无差异曲线一个常用的符合上述假定的效用函数是柯布-道格拉斯效用函数,其形式是:1212(,)u x x Ax x αβ=其中0,01,01A αβ><<<<。
显然,u 是连续的,递增的,凹的。
一个理性的消费者面临的问题是在约束条件下追求效用最大化.............。
其约束条件为:1122p x p x w +≤其中,12,p p 为两种商品的市场价格,w 则表示消费者的财富(或收入)。
给定偏好的单调性,这一约束一定是紧的,也就是1122p x p x w +=。
则消费者的效用最大化问题可以描述为: 12max (,)x u x x1122..s t p x p x w +=上述问题的拉格朗日函数可以写为:121122(,)()L u x x w p x p x λ=+--这一问题的一阶条件为:11u p x λ∂=∂,22up x λ∂=∂ 假定效用函数是凹的,上述条件是充分必要的。
两式相除,得到:1关于偏好,以及偏好与效用效用函数关系的进一步讨论,参见马斯-克莱尔等人,《微观经济理论》,中国社会科学出版社,2001年版;瓦里安,《微观经济学(高级教程)》,经济科学出版社,1997年版。
Ox 1x21212u up p x x ∂∂=∂∂ 上式意味着消费者实现效用最大化的条件是消费两种商品最后一单位的边际效用之比等于两种商品的价格之比。
我们还定义消费者无差异曲线斜率的绝对值为边际替代率(MRS ),表示给定效用水平保持不变(比如u ),少消费一单位商品1,必须增加消费多少单位的商品2,即21dx MRS dx =-。
无差异曲线的数学形式为:12(,)u x x u =,表示使消费者的效用水平达到u 的所有商品组合,两位全微分,得到12120u u dx dx du x x ∂∂+==∂∂,这样我们就得到,2121dx uux x dx ∂∂-=∂∂。
这一结果表明,边际替代率(MRS )等于边际效用之比。
解上述问题,得到消费者效用最大化的解:*1112(,,)x x p p w = *2212(,,)x x p p w =上面两个式子就是消费者的(马歇尔)需求函数,表示当市场价格和财富分别为12,,p p w 时,消费者愿意消费的(效用最大化的)商品1x 和2x 的数量。
显然,**12112212(,)[(,,),(,,)]u x x u x p p w x p p w =为给定价格和财富水平为12,,p p w 时消费者所能达到的最大效用,我们令:12112212(,,)[(,,),(,,)]v p p w u x p p w x p p w =12(,,)v p p w 是一个复合函数,我们将其称为间接效用函数,它表示随着价格和财富水平的变化,消费者所能够实现的最大效用的变化。
下面我们给出两个特例: 特例1:柯布-道格拉斯偏好消费者的效用最大化问题为: 12max x Ax x αβ1122..s t p x p x w +=一阶条件为:1121A x x p αβαλ-=和1122A x x p αββλ-=,两式相除得到:2112x p x p αβ=将约束条件代入,可以得到:()*11w x p ααβ=+,()*22w x p βαβ=+。
特例2:拟线性偏好如果消费者的偏好是拟线性的,那么她的效用函数的形式为:1212(,)()u x x x x φ=+,这时,给定相对价格不变,消费者愿意消费的商品2x 的数量*2x 是唯一..的,无论消费者的财富水平怎样变化(只要保证*22w p x ≥)。
为了说明这一点,我们来求消费者的最大化问题: 12max ()x x x φ+1122..s t p x p x w +=一阶条件是:11p λ=,22'()x p φλ=,得到:221'()x p p φ=,则*1221'()x p p φ-=,这意味*2x 仅仅是相对价格的函数,与财富水平无关。
给定相对价格不变,财富的变化只会改变消费者对1x 的消费数量,而不会改变她对2x 的消费数量。
假定22()ln x x φ=,则有:*212x p p =,*111x w p =-。
拟线性偏好非常重要,在公共经济学,特别是公共产品和外部性理论中有广泛的应用。
附录2A.2:生产集,生产函数,成本函数和生产可能性边界现在我们考察企业的行为。
企业总是在特定的技术约束下将投入品转化为产品,从而可行的生产计划总是受到特定技术的约束。
我们把在技术上可行的所有的投入和产出组合(生产计划)的集合称作生产集...,通常用Y 表示。
如图2A -2,假定只有一种投入品z ,一种产品y ,图中的阴影部分就是生产集。
通常,我们假定生产集是一个非空的闭集,也就是说生产集包括它的边界,这条边界线所确定的函数就是生产函数....,用()y f z =表示。
这样,我们就可以把生产集Y 写成:{}(,):()0,0Y z y y f z z =-≤≥。
我们还假定生产集是凸的,也就是任意两个可行的生产计划的线性组合一定是可行的。
可以证明,对于单一产出的技术,生产集是凸的等价于生产函数()y f z =是凹的2。
图2A -2 生产集为了考察企业在成本约束下的最优投入品组合,我们现在假定存在两种投入要素,1z 和2z ,生产函数为12(,)y f z z =。
企业面临的问题是给定成本约束,选择最优的投入品组合,使其产出最大化,即:12max (,)z f z z 1122..s t z z c ωω+=其中,c 为企业的最高成本约束,12,ωω分别为两种投入品的市场价格。
一阶条件是11f z λω∂∂=和22f z λω∂∂=。
假定生产函数是凹的,上述条件是充分必要的。
两式相除,得到:1122f z f z ωω∂∂=∂∂2关于生产集及其与生产函数的关系的进一步讨论参见马斯-克莱尔等人,《微观经济理论》;瓦里安,《微观经济学(高级教程)》。
上式表明两种要素的边际产出之比(即边际技术替代率MRTS )等于要素价格之比。
上述生产最大化问题的一个对偶问题是成本最小化问题,给定产出约束,即:1122min z z z ωω+..s t12(,)f z z y =其中,y 为企业的最低产出约束。
一阶条件同样是11f z λω∂=和22f z λω∂=,将其代入约束条件,可以解得:*1112(,,)z z y ωω= *2212(,,)z z y ωω=上面两个式子就是所谓的条件要素需求函数........。
令: 12(,,)c y ωω=12**12z z ωω+=11122212(,,)(,,)z y z y ωωωωωω+ 则12(,,)c y ωω为企业的成本函数....,表示给定要素价格和产出要求下的最小成本。
如果生产函数是凹的,可以证明成本函数对于产量y 是凸的。
现在我们转向企业的利润最大化问题,即在给定产品和投入品市场价格的前提下,选择产量使利润最大化。
上述问题可以表示为:12max (,,)y py c y ωω-这一问题的一阶条件是p c y =∂∂,由于目标函数对y 是凹的,这一条件是充分必要的。
意味着利润最大化的条件是选择产量使边际成本等于价格。
现在我们考虑两种产品的情况,为了和上节一致,分别用1x 和2x 表示这两种产品。
生产函数分别为:112112(,)x f z z =和222212(,)x f z z =,可以分别解得两种产品的要素需求函数:*12(,,)j j l l j z z x ωω=, 1,2;1,2l j == 假定投入品总量分别为1z 和2z ,且被完全充分利用,则有:12121122(,,)(,,)l l l z z x z x ωωωω=+, 1,2l = 图2A -3画出了所有可能的两种产品生产组合(我们不考虑负产出),称为生产可能性.....集.,其中FF 曲线被称为生产可能性边界.......,它表示当资源(所有投入品)被充分利用时,两种产品所有的可能性组合,也就是,随着其中一种产品的产量变化,另一种产品所能获得的最大产量的变化轨迹。
图2A -3 生产可能性集我们将生产可能性边界的斜率的绝对值定义为边际转换率.....(MRT ),表示当资源充分利用时,多生产一单位1x ,需要放弃多少单位的2x 。
一般用生产转换函数12(,)0F x x =来表示生产可能性边界,则生产可能性集就可以写作:{}12121,2(,):(,)0,0x x F x x x ≤≥且。
我x 1x 2F们通常假定生产可能性集是一个凸集,假定12(,)F x x 是一个凸函数。
对生产转换函数两边全微分,得到:12120F F dx dx x x ∂∂+=∂∂ 这意味着:2121dx FFMRT x x dx ∂∂=-=∂∂。
另外,经济学中还有一个常用的结论,就是边际转换率等于边际成本之比。
现在我们来证明这个结论:两种产品的成本函数可以表示为:1211122212(,,)(,,)(,,),j j j j j j c x z x z x ωωωωωωωω=+1,2j =则有:121212121122111211122221212122(,,)(,,)[(,,)(,,)][(,,)(,,)]c x c x z x z x z x z x ωωωωωωωωωωωωωω+=+++ 在生产可能性边界上,投入品被充分利用,这意味着:121212112212(,,)(,,)c x c x z z ωωωωωω+=+令上式两边对12(,)x x 全微分,得到:1212120c c dx dx x x ∂∂+=∂∂ 这意味着:122121dx c c MRT x x dx ∂∂=-=∂∂。
2.1.2 福利经济学第一定理:数学证明本节我们对福利经济学第一定理给出一个简化的数学证明。
读者应该将本节和附录2A.1和2A.2结合起来学习。
首先我们给出帕累托最优的数学条件。
假定存在两个消费者A 和B ,两个企业1和2,分别生产商品1x 和2x 。