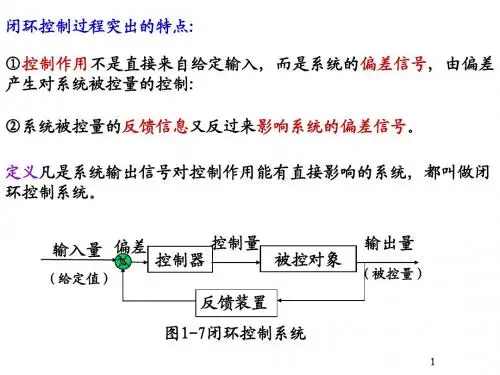
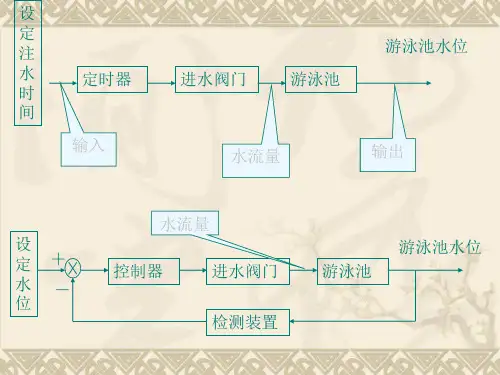
其中, 系数a、b 可以是常数, 也可以是时变系数;r(t) 表示输入 ;c(t) 表示输出。 9
线性系统也可细分成两类: 1)系统微分(或差分)方程的系数均为常数,称为线性定常 系统。 定常特性:系统的响应曲线形状, 只取决于具体的输入, 而与输入的时间起点无关。 2)微分(或差分)方程的系数有时间的函数,则称为线性时 变系统. 至少有一个系统组成元件静特性是斜率随时间变化的直线 。
1.系统分析 (1) 建立系统的数学模型。 (2) 分析系统的性能, 计算三大性能指标是否满足要求 (3) 分析参数变化对上述性能指标的影响,决定如何合理 地选取。
20
2. 系统的设计
步骤如下 :
(1)根据要求的性能指标,综合出系统应有的数学模型。
(2)根据已知的被控对象,求出对象的数学模型, 并画出系 统结构图. (3)按结构图与数学模型关系, 根据己知部分和系统应有 的数学模型,求出控制器的数学模型和控制规律。 (4)各部分结构确定后, 按己定结构求出系统数学模型, 进行性能分析, 验证它在各种信号作用下是否满足要求, 以便修正。 (5)结构参数最终确定后, 可进行实验仿真, 若效果理想 即可制作样机。
图1-11典型的自动控制系统方框图 由被控量通过反馈元件所产生的信号, 它是被控量的函数
5
由系 1.2.3 反馈控制系统的组成和术语
是希望 也称校正元件或控制 典型的自动控制系统一般都是由参考输入元件、比较元件、控 的响应 器、调节器.由于作 也称希望的响 制元件、执行元件、被控对象以及反馈元件六个基本单元组成 值(理 用误差往往十分微弱 应值, 它是理 .每个基本单元都用一个方块表示, 信号传递方向用箭头表示, 想输出 , 一般需要进行幅值 想化系统所产 传递方向都是单向不可逆的, 指向方块的箭头表示输入信号 )与被 和功率的放大, 并将 生的理想响应 离开方块的箭头表示输出信号 控量之 它转换成适于执行机 差 . 构工作的信号; 另外 cr(t) (t) + 理想化系统 由于对系统性能的要 控制元件的输出作用到执行元件, 系统 参 求, 需对作用误差信 执行元件再直接作用于被控对象, 考 比较输入 误差 号进行运算处理.在 输 使被控对象随参考输入而变化如阀 入 一般的控制系统中, r(t) 偏差 控制 门、伺服电动机等 执行 参考输 控制器常采用 PID + 被控对象 c(t) 元件 入元件 b(t) e(t) 元件 控制器 被 指系统中被控制的设备或过程, 主 控 反 它能完成特定的动作或生产任务 量 反馈元件