四年级下册数学试题-思维训练：三角形等积变形(下)(含答案)全国通用

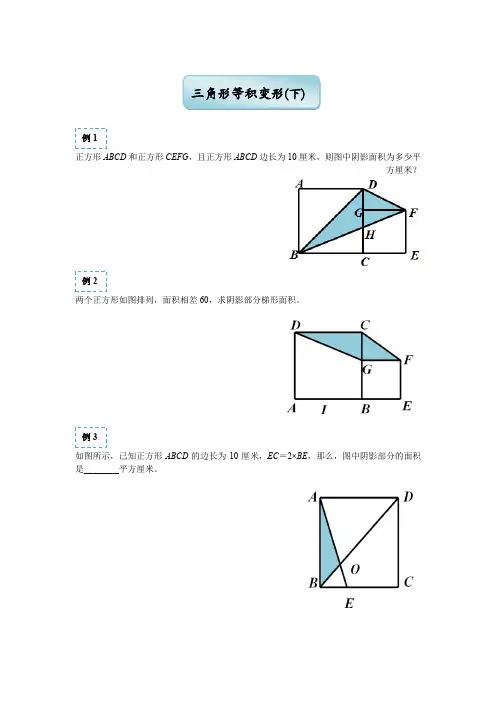
正方形ABCD和正方形CEFG，且正方形ABCD边长为10厘米，则图中阴影面积为多少平方厘米？两个正方形如图排列，面积相差60，求阴影部分梯形面积。

如图所示，已知正方形ABCD的边长为10厘米，EC＝2×BE，那么，图中阴影部分的面积是________平方厘米。

例3例2例1三角形等积变形(下)如图，已知三角形ABC面积为1，延长AB至D，使BD＝AB；延长BC至E，使CE＝2BC；延长CA至F，使AF＝3AC，求三角形DEF的面积。

如图，ABCD为平行四边形，EF平行AC，如果△ADE的面积为4平方厘米。

求三角形CDF的面积。

如图，在四边形ABCD中，对角线AC、BD交于E，且AF＝CE，BG＝DE，如果四边形ABCD 面积是1，求△EFG的面积？例6例5例4测试题1．如图，长方形ABCD的面积是1，M是AD边的中点，N在AB边上，且2AN BN。

那么，阴影部分的面积是多少？2．如图，梯形ABCD被它的一条对角线BD分成了两部分。

三角形BDC的面积比三角形ABD 的面积大10平方分米。

已知梯形的上底与下底的长度之和是15分米，它们的差是5分米。

求梯形ABCD的面积。

ADB C 3．图中两个正方形的边长分别是6厘米和4厘米，则图中阴影部分三角形的面积是（）平方厘米。

4．正方形ABCD和正方形CEFG，且正方形ABCD边长为10厘米，则图中阴影面积为多少平方厘米？HGFEBA5．如图，已知三角形ABC 面积为1，延长AB 至D ，使BD AB =；延长BC 至E ，使2CE BC =；延长CA 至F ，使2AF AC =，求三角形DEF 的面积。

答案1．A M连接BM ，因为M 是中点所以ABM ∆的面积为14又因为2AN BN =，所以ANM ∆的面积为1114312⨯=，又因为BDC ∆面积为12，所以阴影部分的面积为：115112212--= 2．bDCBA如右图，作AB 的平行线DE 。

小学四年级奥数题三角形的等积变形及答案【三篇】【第一篇】1. 三角形把一个等边三角形分别分成8块和9块形状、大小都一样的三角形.分析分成8块的方法是：先取各边的中点并把它们连接起来，得到4个大小、形状相同的三角形，然后再把每一个三角形分成一半，得到如下左图所示的图形.分成9块的方法是：先把每边三等分，然后再把分点彼此连接起来，得到加上右图所示的符合条件的图形.2.比较比较下面两个积的大小：A＝987654321×123456789，B＝987654322×123456788.分析经审题可知A的第一个因数的个位数字比B的第一个因数的个位数字小1，但A的第二个因数的个位数字比B的第二个因数的个位数字大1.所以不经计算，凭直接观察不容易知道A和B哪个大.但是无论是对A或是对B，直接把两个因数相乘求积又太繁，所以我们开动脑筋，将A和B先进行恒等变形，再作判断.解： A＝987654321×123456789＝987654321×（123456788＋1）＝987654321×123456788＋987654321.B＝987654322×123456788＝（987654321＋1）×123456788＝987654321×123456788＋123456788.因为 987654321＞123456788，所以 A＞B.【第二篇】如图，四边形ABCD和四边形DEFG都是正方形，已知三角形AFH的面积为6平方厘米，求三角形CDH的面积．三角形面积答案：通常求三角形的面积，都是先求它的底和高．题目中没有一条线段的长度是已知的，所以我们只能通过创造等积的方法来求．直接找三角形HDC 与三角形AFH 的关系还很难，而且也没有利用"四边形ABCD和四边形DEFG 是正方形"这一条件．我们不妨将它们都补上梯形DEFH 这一块．寻找新得到大三角形CEF 和大直角梯形DEFA 之间的关系．经过验算，可以知道它们的面积是相等的．从而得到三角形 HDC与三角形AFH面积相等，也是6平方厘米．【第三篇】如下图，BE=2AB，BC=CD。