当前位置：文档之家 › 2015中考夺分自主复习课件_第20讲锐角三角函数(共40张PPT)

2015中考夺分自主复习课件_第20讲锐角三角函数(共40张PPT)

  • 格式：ppt
  • 大小：2.81 MB
  • 文档页数：40

下载文档原格式

  / 40

合集下载

《锐角三角函数》课件

《锐角三角函数》课件
锐角三角函数图像与性质
正弦函数图像及性质
周期性
振幅
相位
图像特点
正弦函数具有周期性，周期为2π。
正弦函数的相位表示函数在水平方向上的移动，通过调整相位可以得到不同位置的正弦波。
正弦函数的振幅为1，表示函数在垂直方向上的波动范围。
正弦函数的图像是一条连续的、平滑的曲线，呈现周期性的波动。
余弦函数图像及性质
202X
单击此处添加副标题内容
《锐角三角函数》ppt课件
汇报日期
汇报人姓名
目录
锐角三角函数基本概念
单击此处添加文本具体内容，简明扼要的阐述您的观点。
锐角三角函数图像与性质
单击此处添加文本具体内容，简明扼要的阐述您的观点。
锐角三角函数运算规则
单击此处添加文本具体内容，简明扼要的阐述您的观点。
锐角三角函数在实际问题中应用
乘法运算规则
两个锐角三角函数的除法运算，通常转化为同角三角函数的除法运算，再利用同角三角函数的基本关系式进行化简。
除法运算规则
按照先乘除后加减的运算顺序进行乘除混合运算，注意运算过程中的化简和约分。
乘除混合运算规则
复合运算规则
复合函数的定义域
复合函数的值域
复合函数的单调性
复合函数的周期性
01
02
03
钝角三角函数定义
探讨了钝角三角函数的性质，如取值范围、增减性等，以及与锐角三角函数的异同点。
钝角三角函数的性质
介绍了在直角情况下，一些特殊角的三角函数值，如0°、30°、45°、60°、90°等，以及如何利用这些特殊值进行计算和证明。
直角情况下的特殊值
感谢观看
THANKS
渐近线与间断点
02

锐角三角函数复习课课件

锐角三角函数复习课课件

90度角
总结词
正弦值和余弦值不存在，正切值为无穷大
详细描述
在90度角时，正弦函数值和余弦函数值都不存在，因为无法定义与x轴的角度；正切函数值为无穷大 ，因为在直角三角形中，对边长度可以无限小而保持与斜边的比值不变。
03
锐角三角函数的图像与性质
正弦函数图像
总结词
正弦函数图像是一个周期函数，其图像在直角坐标系中呈波 浪形。
用三角函数来处理角度和旋转。
05
常见题型解析与解题技巧
选择题
• 题型特点：选择题通常考察学生对锐角三角函数基础知识的理 解和应用，题目会给出一些具体的数值或图形，要求选择正确 的答案。
选择题
排除法
根据题目给出的选项，逐一排除明显 错误的答案，缩小选择范围。
代入法
对于涉及数值计算的题目，可以将选 项中的数值代入题目中，通过计算验 证答案的正确性。
在研究磁场和电场时，我们经常需要使用锐 角三角函数来描述场的方向和强度。
日常生活中的问题
建筑和设计
在建筑设计、工程规划和土木工程中，锐角 三角函数用于计算角度、高度和距离等参数 ，以确保结构的稳定性和安全性。
游戏和娱乐
在许多游戏和娱乐活动中，锐角三角函数也 起着重要作用。例如，在制作动画、设计游 戏关卡或创建虚拟现实环境时，我们需要使
总结词
正弦值为0，余弦值和正切值不存在
详细描述
在0度角时，正弦函数值为0，表示射线与x轴重合；余弦函数值不存在，因为无 法定义与x轴的角度；正切函数值也不存在，因为没有对边形成直角三角形。
30度角
总结词
正弦值为0.5，余弦值为0.866，正切值为1/3
详细描述
在30度角时，正弦函数值为0.5，表示对边长度为斜边长度的一半；余弦函数值 为0.866，表示邻边长度为斜边长度的一半的平方根；正切函数值为1/3，表示对 边长度与邻边长度的比值。

九年级三角函数复习课件PPT(共19张PPT)

九年级三角函数复习课件PPT(共19张PPT)

则a= 2 ，∠B= 60°，∠A= 30°.
5.如果 cos A 1 3 tan B 3 0
2
那么△ABC是（ D ）
A.直角三角形 C.钝角三角形
B.锐角三角形 D.等边三角形
6.直角三角形纸片的两直角边BC为6， AC为8,现将△ABC，按如图折叠，使点A 与点B重合，折痕为DE，则tan∠CBE的值
在Rt△PAD中，∵∠PAD＝90°－60°＝30°，
AD 3PD, 12 x 3x,
x 12 6( 3 1) 18. 3 1
∴渔船不改变航线继续向东航行，有触礁危险．
8.如图，甲船在港口P的北偏西60°方向，距港口80海里的A 处，沿AP方向以12海里/时的速度驶向港口P．乙船从港口P 出发，沿北偏东45°方向匀速驶离港口P，现两船同时出发， 2小时后乙船在甲船的正东方向．求乙船的航行速度．
谢 谢！
让我们共同进步
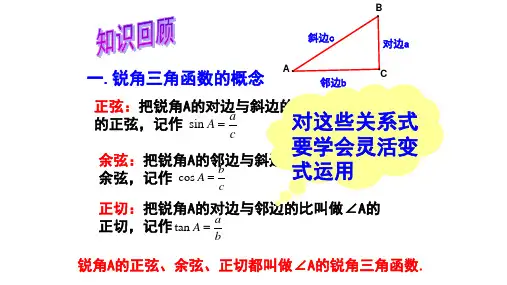
（2）两锐角的关系：∠A十∠B＝90°
（3）边角的关系：sin A a cos A b tan A a
c
c
b
归纳：只要知道其中的2个元素（至少有一个是边），
就可以求出其余3个未知元素.
四.解直角三角形的应用
1.仰角和俯角
在进行测量时， 从下向上看，视线与水平线的夹角叫做仰角； 从上往下看，视线与水平线的夹角叫做俯角.
视线
铅 直
仰角
线
俯角
水平线
视线
2.坡度、坡角
坡角：坡面与水平面的夹角叫做坡角，用字母α表示.
坡度（坡比）：坡面的铅
直高度h和水平距离l的
比叫做坡度，用字母i表
示，则 i h tan
l

【数学课件】2015中考数学总复习：锐角三角函数(人教版)

【数学课件】2015中考数学总复习：锐角三角函数(人教版)
考点聚焦 归类探究 回归教材
1、做老师的只要有一次向学生撒谎撒漏了底，就可能使他的全部教育成果从此为之毁灭。——卢梭 2、教育人就是要形成人的性格。——欧文 3、自我教育需要有非常重要而强有力的促进因素——自尊心、自我尊重感、上进心。——苏霍姆林斯基 4、追求理想是一个人进行自我教育的最初的动力，而没有自我教育就不能想象会有完美的精神生活。我认为，教会学生自己教育自己，这是一种 最高级的技巧和艺术。——苏霍姆林斯基 5、没有时间教育儿子——就意味着没有时间做人。——（前苏联）苏霍姆林斯基 6、教育不是注满一桶水，而且点燃一把火。——叶芝 7、教育技巧的全部奥秘也就在于如何爱护儿童。——苏霍姆林斯基 8、教育的根是苦的，但其果实是甜的。——亚里士多德 9、教育的目的，是替年轻人的终生自修作准备。——R.M.H. 10、教育的目的在于能让青年人毕生进行自我教育。——哈钦斯 11、教育的实质正是在于克服自己身上的动物本能和发展人所特有的全部本性。——（前苏联）苏霍姆林斯基 12、教育的唯一工作与全部工作可以总结在这一概念之中——道德。——赫尔巴特 13、教育儿童通过周围世界的美，人的关系的美而看到的精神的高尚、善良和诚实，并在此基础上在自己身上确立美的品质。——苏霍姆林斯基 14、教育不在于使人知其所未知，而在于按其所未行而行。——园斯金 15、教育工作中的百分之一的废品，就会使国家遭受严重的损失。——马卡连柯 16、教育技巧的全部诀窍就在于抓住儿童的这种上进心，这种道德上的自勉。要是儿童自己不求上进，不知自勉，任何教育者就都不能在他的身 上培养出好的品质。可是只有在集体和教师首先看到儿童优点的那些地方，儿童才会产生上进心。——苏霍姆林斯基 17、教育能开拓人的智力。——贺拉斯 18、作为一个父亲，最大的乐趣就在于：在其有生之年，能够根据自己走过的路来启发教育子女。——蒙田 19、教育上的水是什么就是情，就是爱。教育没有了情爱，就成了无水的池，任你四方形也罢、圆形也罢，总逃不出一个空虚。班主任广博的爱 心就是流淌在班级之池中的水，时刻滋润着学生的心田。——夏丐尊 20、教育不能创造什么，但它能启发儿童创造力以从事于创造工作。——陶行知

初三数学《锐角三角函数》优秀教学课件

初三数学《锐角三角函数》优秀教学课件
3 应用
锐角三角函数广泛应用于物理、工程、计算机图形学等领域。
三角函数的定义及分类
定义பைடு நூலகம்
正弦、余弦、正切、正割和 余割是根据三角形的边长关 系定义的函数。
分类
三角函数可分为基本三角函 数和带角的三角函数，每个 函数都有不同的性质和应用。
图像
不同函数在坐标系上的图像 展示了它们的周期性、对称 性和变化规律。
角度制与弧度制的转换
1 角度制
2 弧度制
常用角度单位，用度数表示。
另一种角度单位，用弧长与半径的比值表示。
3 转换方法
角度制与弧度制之间可通过一定的换算公式进行转换。
正弦函数的图像及基本性质
图像
正弦函数在坐标系中呈现出一条 连续变化的波浪线。
性质
正弦函数的定义域是全体实数， 值域是[-1, 1]，具有周期性和对 称性。
正切函数的图像及基本性质
1
图像
正切函数在坐标系中形成一系列连续交叉的直线。
2
性质
正切函数的定义域是所有切点的横坐标全体，值域是所有实数。
3
特性
无定义点、无界性和奇偶性是正切函数的特别性质。
正割函数、余割函数的图像及基本性质
1 正割函数
正割函数形成一组连续的 曲线，与余弦函数图像对 称。
2 余割函数
余割函数形成一组连续的 曲线，与正弦函数图像对 称。
3 性质
正割和余割函数分别是余 弦和正弦函数的倒数。
三角函数的周期性质
周期
三角函数的图像在一定范围内 呈现出重复的模式，这个范围 称为函数的周期。
周期公式
不同三角函数的周期可通过一 定的公式进行计算。
变化规律
周期性质决定了三角函数的重 复模式和增减变化规律。

中考人教版数学考前热点冲刺指导课件：《第20讲 锐角三角函数 》 (共23张PPT)

中考人教版数学考前热点冲刺指导课件：《第20讲 锐角三角函数 》 (共23张PPT)
第20讲┃ 锐角三角函数
┃考向互动探究与方法归纳┃
┃典型分析┃
例 如图20－9，大楼AD高30 m，远处有一塔BC，某 人在楼底A处测得塔顶的仰角为60°，爬 到楼顶D测得塔顶的仰角为30°.求塔高BC 为多少？
[解析] 用AC表示出BE、BC长，根据BC－ BE＝30得方程求AC，进而求得BC长．
第20讲┃ 锐角三角函数
如图20－10，热气球的探测器显示，从热气球看 一栋高楼顶部的仰角为60°，看这栋高楼底部的俯角为30°， 热气球与高楼的水平距离为66 m，这栋高楼有多高？(结果精确 到0.1 m，参考数据： 3≈1.73)
图20－10 第20讲┃ 锐角三角函数
解：如图，过点A作AD⊥BC，垂足为D，
13、He who seize the right moment, is the right man.谁把握机遇，谁就心想事成。2021/9/142021/9/142021/9/142021/9/149/14/2021 •14、谁要是自己还没有发展培养和教育好，他就不能发展培养和教育别人。2021年9月14日星期二2021/9/142021/9/142021/9/14 •15、一年之计，莫如树谷；十年之计，莫如树木；终身之计，莫如树人。2021年9月2021/9/142021/9/142021/9/149/14/2021 •16、教学的目的是培养学生自己学习，自己研究，用自己的头脑来想，用自己的眼睛看，用自己的手来做这种精神。2021/9/142021/9/14September 14, 2021 •17、儿童是中心，教育的措施便围绕他们而组织起来。2021/9/142021/9/142021/9/142021/9/14
第20讲┃ 锐角三角函数
7．计算：12－1－2cos30°＋ 27＋(2－π)0.

中考专项复习锐角三角函数88页PPT

中考专项复习锐角三角函数88页PPT
13、遵守纪律的风气的培养，只有领 导者本 身在这 方面以 身作则 才能收 到成效 。—— 马卡连 柯 14、劳动者的组织性、纪律性、坚毅 精神以 及同全 世界劳 动者的 团结一 致，是 取得最 后胜利 的保证 。—— 列宁 摘自名言网
15、机会是不守纪律的。。——华盛顿 17、一个人即使已登上顶峰，也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人，而用人最大的突破在于信任人。——马云 19、自己活着，就是为了使别人过得更美好。——雷锋 20、要掌握书，莫被书掌握；要为生而读，莫为读而生。——布尔沃
END
中考专项复习锐角三角函数
11、战争满足了，或曾经满足过人的 好斗的 本能， 但它同 时还满 足了人 对掠夺 ，破坏 以及残 酷的纪 律和专 制力的 欲望。 ——查·埃利奥 特 12、不应把纪律仅仅看成教育的手段 。纪律 是教育 过程的 结果， 首先是 学生集 体表现 在一切 生活领 域—— 生产、 日常生 活、学 校、文 化等领 域中努 力的结 果。— —马卡 连柯(名 言网)
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

图 20－1 第20讲┃ 锐角三角函数
【归纳总结】
如图 20－2，在 Rt△ABC 中，∠C＝90°，∠A，∠B， a b ∠C 的对边分别为 a，b，c，则 sinA＝________ ，cosA＝ ， c c a tanA＝________ ． b
图 20－2 第20讲┃ 锐角三角函数
考点2
第20讲┃ 锐角三角函数
【归纳总结】
如图 20－3，在 Rt△ABC 中，∠C＝90°，∠A，∠B，∠C 的对边分别为 a，b，c，则有下列关系： (1)三边的关系：a2＋b2＝________ ； c2 (2)角的关系：∠A＋∠B＝________ 90° ； b a (3)边与角的关系：sinA＝cosB＝ ，sinB＝cosA＝________ ， c c a tanA＝ ； b 1 ab ． (4)面积关系：S△ABC＝________ 2
第20讲
锐角三角函数
┃考点自主梳理与热身反馈 ┃ 考点1 锐角三角函数 1．在 Rt△ABC 中，∠C＝90°，CD 是斜边 AB 上的中 线，已知 CD＝5，AC＝6，则 tanB 的值是 ( C ) 4 3 3 4 A. B. C. D. 5 5 4 3 2．如图 20－1，在 Rt△ABC 中，∠C＝90°，若 AB＝ 1 3 2，BC＝1，则 sinA＝________ ，cosA＝________ ． 2 2
图 20－3
第20讲┃ 锐角三角函数
考点4
解直角三角形的应用
1．如图 20－4 是一水库大坝横断面的一部分，坝高 h＝ 6 m，迎水斜坡 AB＝10 m，斜坡的坡角为 α，则 tanα 的值
3 为________ ． 4
图 20－4
第20讲┃ 锐角三角函数
2．如图 20－5，大楼 AD 高 30 m，远处有一座塔 BC，某 人在楼底 A 处测得塔顶的仰角为 60°，爬到楼顶 D 测得塔顶 的仰角为 30°，则塔高 BC 为________m. 45
3 2
3 ______ 3
1 2 3
1
第20讲┃ 锐角三角函数
考点3
解直角三角形的基本关系
1．在 Rt△ABC 中，∠C＝90°，∠A，∠B，∠C 所对 的边分别为 a，b，c，则下列关系正确的是 ( C ) A．c＝a· sinA B．c＝a· cosA a a C．c＝ D．c＝ sinA cosA 2．在△ABC 中，a，b，c 分别是∠A，∠B，∠C 的对 边，如果 a2＋b2＝c2，那么下列结论正确的是 ( A ) A．csinA＝a B．bcosB＝c C．atanA＝b D．ctanB＝b
[解析] 旋转后的三角形与原三角形全等，得∠B′＝ ∠B.将∠B 放在以 BC 为斜边、 直角边在网格线上的直角三 1 角形中，∠B 的对边为 1，邻边为 3，则 tanB′＝tanB＝ . 3
第20讲┃ 锐角三角函数
[中考点金]
求锐角的三角函数值的常用方法是根据锐角三角函 数的定义，求关于该角相应边的比值．在具体解题过程 中，也常用转化角或转化线段的方法．
第20讲┃ 锐角三角函数
变式题 [2014· 兰州] 如图 20－10 所示， 在 Rt△ABC 中， ∠C＝90°，BC＝3，AC＝4，那么 cosA 的值等于 ( D )
图 20－10 3 4 3 4 A. B. C. D. 4 3 5 5 [解析] ∵在 Rt△ABC 中， ∠C＝90°， AC＝4， BC＝3，
┃考向互动探究与方法归纳┃
探究一 求锐角的三角函数值
例 1 如图 20－9， A， B， C 三点在正方形网格线的格点上， 若将△ACB 绕着点 A 逆时针旋转得到△AC′B′， 则 tanB′的值 为 ( B )
1 A. 2
1 B. 3
图 20－9 1 2 C. D. 4 4 第20讲┃ 锐角三角函数
∴AB＝ AC2＋BC2＝ 42＋32＝5， AC 4 ∴cosA＝ ＝ .故选 D. AB 5
第20讲┃ 锐角三角函数
探究二 解直角三角形在测量中的应用
例 2 如图 20－11，小刚同学在南州广场上观测新华书 店楼房墙上的电子屏幕 CD，点 A 是小刚的眼睛，测得屏幕 下端 D 处的仰角为 30°，然后他正对屏幕方向前进了 6 米 到达 B 处，又测得该屏幕上端 C 处的仰角为 45°，延长 AB 与楼房垂直相交于点 E，测得 BE＝21 米，请你帮小刚求出 该屏幕上端与下端之间的距离 CD.(结果保留根号)图 2Biblioteka －5第20讲┃ 锐角三角函数
【归纳总结】
1．仰角和俯角： 如图 20－6，在视线与水平线所成的角中，视线在水 上方 的角叫仰角； 下方 的角叫 平线________ 视线在水平线________ 俯角．
图 20－6
第20讲┃ 锐角三角函数
2．坡度和坡角： 如图 20－7，坡面的铅直高度(h)和水平宽度(l)的比叫 h 坡度 做坡面的 ________ ，记作 i＝ . 坡面与水平面的夹角叫做 l 坡角 ． ________
图 20－11 第20讲┃ 锐角三角函数
[解析] 在 Rt△BEC 中， 利用等腰直角三角形的性质可 求 CE， 在 Rt△ADE 中， 利用直角三角形边角关系可求 DE， 故 CD＝CE－DE.
解：∵∠CBE＝45°，CE⊥AE， ∴CE＝BE＝21，AE＝BE＋AB＝21＋6＝27. 在 Rt△ADE 中，∠DAE＝30°， 3 ∴DE＝AE×tan30°＝27× ＝9 3. 3 ∴CD＝CE－DE＝21－9 3. 3)米．
特殊角的三角函数值
1 1．sin30°＝________ ． 2 2．若 tanα ＝1，则∠α＝________ 45° ．
第20讲┃ 锐角三角函数
【归纳总结】
锐角 α 锐角三角函数 sinα cosα tanα
30°
1 ______ 2
45° 2 2
2 ______ 2
60°
3 ______ 2
图 20－7
第20讲┃ 锐角三角函数
3．方位角： 北偏东 30° 如图 20－8，由北向东偏 30°读作__ ______ ，由南向 东偏 50°读作____ ____ 西南方向是指______________ 南偏东50 °， 南偏西45° ．
图 20－8
第20讲┃ 锐角三角函数
【知识树】
第20讲┃ 锐角三角函数