浙教版数学七年级上册第7讲 一元一次方程

51一元一次方程浙教版七年级数学上册教案一、教学内容本节课选自浙教版七年级数学上册第七章《一元一次方程》的第一课时。

教学内容主要包括：理解一元一次方程的概念；掌握解一元一次方程的一般步骤；学会运用等式的基本性质解一元一次方程。

二、教学目标1. 知识与技能：使学生理解一元一次方程的概念，掌握解一元一次方程的方法，并能熟练运用。

2. 过程与方法：培养学生分析问题、解决问题的能力，提高学生运用数学知识解决实际问题的能力。

3. 情感态度价值观：激发学生学习数学的兴趣，培养学生的合作意识和探究精神。

三、教学难点与重点重点：一元一次方程的概念，解一元一次方程的方法。

难点：如何运用等式的基本性质解一元一次方程。

四、教具与学具准备教具：黑板、粉笔、教学课件。

学具：练习本、铅笔。

五、教学过程1. 引入：通过一个实践情景，引导学生思考如何解决问题，引出一元一次方程的概念。

例如：小明和小华一起去书店，小明买书花费了20元，小华比小明多买了5本书，花费了40元。

请问小明和小华各买了多少本书？2. 新课讲解：（1）引导学生观察实践情景中的数量关系，发现未知数，列出方程。

（2）讲解一元一次方程的概念，让学生理解方程的组成。

（3）介绍解一元一次方程的一般步骤，引导学生学会运用等式的基本性质解方程。

3. 例题讲解：（1）解方程：3x + 5 = 14。

（2）解方程：5(y 2) = 3(y + 4)。

（2）解方程：2(x 3) + 4 = 3x。

六、板书设计1. 一元一次方程的概念。

2. 解一元一次方程的步骤。

3. 例题及解答过程。

七、作业设计1. 作业题目：（1）解方程：4x 7 = 2x + 9。

（2）解方程：5(2x 3) = 3(3x + 1)。

2. 答案：八、课后反思及拓展延伸2. 拓展延伸：让学生思考一元一次方程在实际生活中的应用，培养学生的数学思维。

重点和难点解析1. 教学内容的针对性：确保教学内容与浙教版七年级数学上册第七章《一元一次方程》的教材内容相符合。

浙江版2019-2020学年度七年级数学上册第5章一元一次方程 5.1 一元一次方程【知识清单】 一、一元一次方程：1.方程：含有未知数的等式叫做方程.2.方程的解：使方程左右两边的值都相等的未知数的值叫做方程的解3.一元一次方程：只含有一个未知数，未知数的次数是1，这样的方程叫做一元一次方程. 二、方程的判定方法归纳：1.判断一个式子是不是方程必须看两点：一是等式，二是含有未知数，二者缺一不可；2.判定一个方程是不是一元一次方程，要看方程是否只含一个未知数并且未知数的指数都是1，而且是整式方程. 【经典例题】例题1、下列方程中，是一元一次方程的是( )A ．x 2-2x =1B ．-5x =0C ．3x +2y =5D ．x =x1【考点】一元一次方程的定义．【分析】根据一元一次方程的定义判断即可．【解答】A 、方程的次数是2次，即不是一元一次方程，故本选项错误；B 、是一元一次方程，故本选项正确；C 、含有两个未知数，即不是一元一次方程，故本选项错误；D 、不是整式方程，即不是一元一次方程，故本选项错误； 故选B ．【点评】本题考查了对一元一次方程的定义的应用，熟练掌握一元一次方程的定义是解决问题的关键．例题2、如果方程(m -2)1-m x+26=0是关于x 的一元一次方程，那么m 的取值是______．【考点】一元一次方程的定义．【分析】只含有一个未知数(元)，并且未知数的指数是1(次)的方程叫做一元一次方程，高于一次的项系数是0．据此可得出关于m 的方程，继而可求出m 的值． 【解答】由一元一次方程的定义，得⎩⎨⎧=-≠-1102m m ，解得m =-2．故填：-2．【点评】本题主要考查了一元一次方程的定义，只含有一个未知数，未知数的指数是1，一次项系数不是0，这是这类题目考查的重点．【夯实基础】1．下列方程中，是一元一次方程的是( )A ．2x =3y B.y 1＋1=0 C ．2x 2＋3x =2 D. )2(31-x =1 2．下列说法正确的是( )A ．x =-2是方程2x ＋5=0的解B ．y =0是方程0.5(5-2y )=2.5的解C ．方程3x -4=)3(31-x )的解是x =3D ．方程43-x =2的解是x =383．一件高于成本50%标价的上衣，按8折销售仍可获利40元．设这件上衣的成本价为x 元，根据题意，下面所列方程正确的是( )A ．x (1+50%)×0.8-x =30B ． ( x +50%)×0.8-x =30C ．x (1+50%)×0.8=30-xD ．( x +50%)×0.8=30-x 4．关于｜x -2｜=2的说法正确的是 ( )A ．不是方程B ．是方程其解为0C ．是方程其解为4D ．是方程其解为0或45．若关于x 的方程(3k -2)x 2- (3k +2)x +5=0是一元一次方程，则k 的值为 .6．如图，两边都放着物体的天平处于平衡状态，用等式表示天平两边所放物体的质量关系为__ __________．7．下列不是方程的是__________．(填序号)① 1＋2=3； ② 2x ＋1； ③ 2m ＋15=3； ④ x 2－6=0； ⑤ 3x ＋2y =9； ⑥ 3a ＋9＞15.8．已知关于x 的方程5a -2x =9的解为x =3，求代数式(-a )2-2a ＋1的值．9．有甲、乙两支同样长的蜡烛，甲蜡烛可使用12 h ，乙蜡烛可使用10 h ．两蜡烛同时点燃，几小时后乙蜡烛的长度是甲蜡烛长度的三分之一？(列出方程，不必求解)【提优特训】10．若5x -6与2x -8是一个正数两个平方根，则可列方程来表示为( )A ．5x -6=2x -8B ．5x -6+2x -8=0C ．5x +6+2x +8=0D ．5x +6+2x -8=0 11．若方程(3a -2)x 2+bx +c =0是关于x 的一元一次方程，则字母系数a ，b ，c 的值满足( )A ．a =32，b =0，c 为任意数 B ．a ≠32，b ≠0，c =0 C ．a =32，b ≠0，c 为任意数 D ．a =32，b ≠0，c ≠0 12．下列方程中，解为x =-2的方程是( )A ．21x ＋3=x B ． x -2=0 C ．2x =4 D ．321)63(31-=-x x 13．已知单项式-ma 3b m -1与单项式4a 3b 2是同类项，则关于m 的方程一定正确的是( )A ．-m +4=0B ．-m -4=0C ．m -1+2=0D ． m -1=2 14．已知53-m x-1=m 是关于x 的一元一次方程，则这个方程的解 ．15．对于有理数a ，b ，c ，d ，规定一种运算bc ad dbc a -=，如43525342⨯-⨯==-2. 若32331=----x x ，则所得到的方程为 ．16．根据下列条件列出方程． 1.设某数为x : (1)某数的65与-5的和是6； (2)某数的5倍等于该数的2倍与18的差； (3)某数减少20%后比该数的60%小5； (4)比某数的3倍大6的数是12”用方程表示为.2.(1)某长方形的周长是64，长与宽之比为5∶3，则长和宽各是多少？设长方形的长为5x . (2)爸爸今年38岁，比儿子年龄的3倍少4岁，则小明今年几岁？设小明今年x 岁．17．已知关于x 的方程ax 2+x b -3-2=0是一元一次方程，试求x a +b 的值.18．数学课上老师出示了四张卡片，上面分别写着不同的代数式，要求同学们解决下面的问题：用等号将这四张卡片的任意两张卡片上的数或式子连接起来，就会得到等式或方程． (1)你一共能写出几个等式？(2)在这些等式中，有几个一元一次方程？请写出这几个一元一次方程．19．汽车的油箱内储油40kg，已知工作时的耗油以及油箱内的剩油量的关系如表所示工作时间t(h) 耗油量p(kg) 剩油量m(kg)1 2.5 40-2.5=37.52 5 40-5=353 7.5 40-7.5=32.54 10 40-10=30………(1)写出工作10h后，油箱内的剩油量；(2)写出工作t h后，油箱内的剩油量为7.5kg，请你列出关于t的方程(不解方程).20．如图用火柴棒搭正方形，用n表示所搭正方形的个数，从而计算火柴棒的根数，当n=1，所需火柴棒为4根，当n=2，所需火柴棒为7根，当n=3，所需火柴棒为10根，…，请问：(1)第5个图形中火柴棒有多少根？(2)第n个图形中火柴棒有多少根？(3)若有一个图形由781根火柴棒组成，那么这个图形由几个正方形组成？【中考链接】21．(2018•临安)(3分)中央电视台2套“开心辞典”栏目中，有一期的题目如图所示，两个天平都平衡，则三个球体的重量等于()个正方体的重量．A．2 B．3 C．4 D．522．(2018•临沂)任何一个无限循环小数都可以写成分数的形式，应该怎样写呢？我们以无限循环小数7.0 为例进行说明：设7.0 =x ，由7.0 =0.7777…可知，l0x =7.7777…，所以l0x -x =7，解方程，得x =97，于是．得7.0 =97．将63.0 写成分数的形式是 ．参考答案1、D2、B3、A4、D5、326、x+4=107、①②⑥ 10、B 11、C 12、D 13、D 14、-1或3 15、-(x -2)+3(3-x )=3 21、D 22、114 8．已知关于x 的方程5a -2x =9的解为x =3，求代数式(-a )2-2a ＋1的值． 解：∵方程5a -2x =9的解为x =3，∴5a -2×3=9， ∴a =3.∴(-a )2-2a ＋1 =(-3)2-2×3＋1=4.9．有甲、乙两支同样长的蜡烛，甲蜡烛可使用12 h ，乙蜡烛可使用10 h ．两蜡烛同时点燃，几小时后乙蜡烛的长度是甲蜡烛长度的三分之一？(列出方程，不必求解) 解：设x 小时后乙蜡烛的长度是甲蜡烛长度的一半，则1-101x =31(1-121x ). 16．根据下列条件列出方程． 1.设某数为x : (1)某数的65与-5的和是6； (2)某数的5倍等于该数的2倍与18的差； (3)某数减少20%后比该数的60%小5； (4)比某数的3倍大6的数是12”用方程表示为.2.(1)某长方形的周长是64，长与宽之比为5∶3，则长和宽各是多少？设长方形的长为5x . (2)爸爸今年38岁，比儿子年龄的3倍少4岁，则小明今年几岁？设小明今年x 岁． 16．解：1.(1)65x -5=6； (2) 5x =2x -18；(3) (1-20%)x =60%x -5； (4) 3x +6=12；2．解：(1)由长方形的长为3x ，得宽为2x ，则2(5x ＋3x )=64.(2)根据题意，得3x -4=38.17．已知关于x 的方程ax 2+x b -3-2=0是一元一次方程，试求x a +b 的值. 解：∵ax 2+x b-3-2=0是关于x 的一元一次方程，∴a =0，b -3=1， ∴a =0，b =4， ∴x -2=0， ∴x =2. ∴x a +b =24=16.18．数学课上老师出示了四张卡片，上面分别写着不同的代数式，要求同学们解决下面的问题：用等号将这四张卡片的任意两张卡片上的数或式子连接起来，就会得到等式或方程． (1)你一共能写出几个等式？(2)在这些等式中，有几个一元一次方程？请写出这几个一元一次方程． 18． 解：(1)6个．(2)有3个一元一次方程，它们分别是5x -3=-6，6261-=-x ，5x -3=261-x . 19．汽车的油箱内储油40kg ，已知工作时的耗油以及油箱内的剩油量的关系如表所示工作时间t (h) 耗油量p (kg) 剩油量m (kg) 1 2.5 40-2.5=37.5 2 5 40-5=35 3 7.5 40-7.5=32.5 4 10 40-10=30 ………(1)写出工作10h 后，油箱内的剩油量；(2)写出工作t h 后，油箱内的剩油量为7.5kg ，请你列出关于t 的方程(不解方程). 解: (1)40-10×2.5=15；工作10h 后，油箱内的剩油量为15 kg ； (2)根据题意，得40-2.5t =7.5.20．如图用火柴棒搭正方形，用n 表示所搭正方形的个数，从而计算火柴棒的根数，当n =1，所需火柴棒为4根，当n =2， 所需火柴棒为7根，当n =3， 所需火柴棒为10根，…，请问：(1)第5个图形中火柴棒有多少根？(2)第n个图形中火柴棒有多少根？(3)若有一个图形由781根火柴棒组成，那么这个图形由几个正方形组成？解：根据图形特点和题意可得：第1个图形n=1，火柴棒为3×1+1=4根，第2个图形n=2，火柴棒为3×2+1=7根，第3个图形n=3，火柴棒为3×3+1=10根，…(1)第5个图形中火柴棒有3×5+1=16根，(2)第n个图形中火柴棒有3×n+1=(3n+1)根，(3)3n+1=781，解得n=260，答：这个图形由260个正方形组成.。

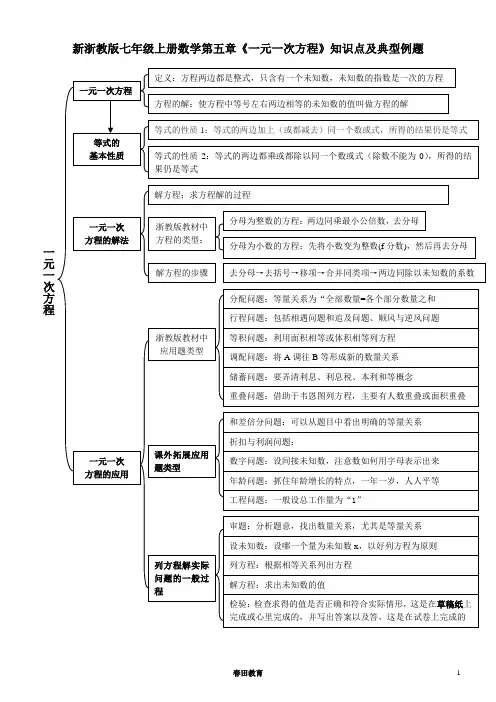
新浙教版七年级上册数学第五章《一元一次方程》知识点及典型例题关于一元一次方程概念的拓展教材中的概念：方程两边都是整式，只含有一个未知数，未知数的指数是一次的方程是一元一次方程，那么 x+2=x+3是一元一次方程吗？从概念上来看，是一元一次方程，但稍作变形，就是2=3，是不是觉得很可笑？因此，一元一次方程的概念应该是：方程两边都是整式，只含有一个未知数，未知数的指数是一次，并且能变形为ax=b （a ≠0，a 、b 均为常数）的方程是一元一次方程，也就是说，一元一次方程一定只有一个解。

关于用方程解应用题的秘诀：相关条件设未知数，剩余条件列方程将考点与相应习题联系起来考点一、判断方程是不是一元一次方程及一元一次方程概念的简单应用 1、下列等式中是一元一次方程的是（ ）A ．3x=y-1B ．2(1)21x x -=+C ．3(x-1)= -2x-3D ．3x 2-2=3E ．11x x=+ 2、在方程23=-y x ，021=-+x x ，2121=x ，0322=--x x 中一元一次方程的个数为（ ） A ．1个 B ．2个 C ．3个 D ．4个 3、如果06312=+--a x是一元一次方程，那么=a ，方程的解为 。

（特别注意）考点二、关于在解方程过程中的某些变形问题，只能以选择题的形式出现 1、已知等式523+=b a ，则下列等式中不一定．．．成立的是（ ） （A ）;253b a =- （B ）;6213+=+b a （C ）;523+=bc ac （D ）.3532+=b a 2、解方程2631xx =+-，去分母，得（ ） （A ）133x x --= （B ）633x x --= （C ）633x x -+= （D ）133x x -+=3、下列方程变形中，正确的是（ ）（A ）方程1223+=-x x ，移项，得;2123+-=-x x （B ）方程()1523--=-x x ，去括号，得;1523--=-x x （C ）方程2332=t ，未知数系数化为1，得;1=t （D ）方程110.20.5x x --=化成101010125x x --= 考点三、解一元一次方程（1）x x 3.15.67.05.0-=-； （2）错误!未找到引用源。

一元一次方程浙教版课件一、教学内容本节课选自浙教版《数学》七年级上册第三章“一元一次方程”的第一节，内容包括方程的定义、一元一次方程的识别与解法，重点讲解方程的解的概念以及如何通过移项、合并同类项等方法求解一元一次方程。

二、教学目标1. 理解方程的概念，能够识别一元一次方程。

2. 学会解一元一次方程的基本方法，并能应用于实际问题。

3. 培养学生的逻辑思维能力和解决问题的能力。

三、教学难点与重点教学难点：一元一次方程的解法，特别是移项和合并同类项。

教学重点：一元一次方程的概念及其解法。

四、教具与学具准备教具：黑板、粉笔、PPT课件。

学具：学生用练习本、铅笔。

五、教学过程1. 实践情景引入通过购物找零等生活中的实例，引出方程的概念。

2. 知识讲解（1）讲解方程的定义，让学生明白方程是表示两个量相等的数学式子。

（2）介绍一元一次方程，强调只含有一个未知数，且未知数的最高次数为一。

3. 例题讲解以“3x 7 = 11”为例，讲解移项和合并同类项的步骤，展示如何求解一元一次方程。

4. 随堂练习学生自主完成PPT上呈现的练习题，教师进行解答指导。

5. 课堂小结梳理本节课所学的知识点，强调一元一次方程的解法步骤。

六、板书设计1. 方程的定义2. 一元一次方程的识别3. 求解一元一次方程的步骤：移项、合并同类项七、作业设计1. 作业题目：（1）求解下列方程：2x + 5 = 3x + 24 3(x 1) = 5x（2）小华的年龄比小明大6岁，过3年后，小华的年龄是小明的两倍。

求小明和小华现在的年龄。

2. 答案：（1）2x + 5 = 3x + 22x 3x = 2 5x = 3x = 3（2）设小明现在的年龄为x岁，则小华现在的年龄为x + 6岁。

过3年后，小明的年龄为x + 3岁，小华的年龄为x + 9岁。

根据题意，有：x + 9 = 2(x + 3)x + 9 = 2x + 6x = 3小明现在3岁，小华现在9岁。