模拟信号的数字传输.
- 格式:doc
- 大小:727.00 KB
- 文档页数:26




数字信号传输与模拟信号传输的比较随着科技的进步与发展,无线通信以及数据传输方式也得到了极大的改善。
在通信领域中,数字信号传输与模拟信号传输是两种常见的方式。
本文将比较数字信号传输与模拟信号传输的优缺点,并分析其应用范围。
(一)数字信号传输与模拟信号传输的基本概念和原理1. 数字信号传输:数字信号是离散信号,它的状态是由一系列离散值组成的。
在传输过程中,数字信号可以通过编码和译码的方式将信号转换为二进制数字,再通过通信介质传输。
2. 模拟信号传输:模拟信号是连续信号,它的状态可以在一个连续范围内取值。
模拟信号的传输是通过传感器将信号转换为电压或电流的变化,并通过通信介质传输。
(二)1. 噪音抗干扰能力:- 数字信号传输的优点在于它具有较高的噪音抗干扰能力。
由于数字信号是离散的,因此在传输过程中能够更好地抵抗噪音的干扰。
而模拟信号由于其连续性,对于噪音和干扰更加敏感。
2. 信号传输的准确性:- 数字信号的传输准确性较高,由于其离散性,数字信号的传输不容易发生失真。
而模拟信号的传输容易受到干扰,可能会发生失真现象。
3. 传输距离:- 数字信号的传输距离相对较远,通过使用中继设备和调制解调器等方式可以将信号传输到更远的地方。
而模拟信号的传输距离相对较短,传输距离受到信号衰减和干扰的影响。
4. 带宽利用:- 数字信号传输可以更有效地利用带宽资源,通过压缩和编码技术,数字信号传输可以在相同的带宽下传输更多的信息。
而模拟信号传输由于其连续性,需要使用较宽的频带来传输相同数量的信息。
(三)数字信号传输与模拟信号传输的应用范围1. 数字信号传输的应用范围:- 数字信号传输主要应用于各种数字通信领域,包括移动通信、互联网、数字电视、数字广播以及以太网等。
数字信号传输对于数据的精确传输非常重要,可以更好地抵抗干扰。
2. 模拟信号传输的应用范围:- 模拟信号传输广泛应用于音频和视频领域,如模拟音频传输、视频传输、无线电广播等。

实验三 模拟信号的数字传输仿真一、实验目的1、 掌握PCM 的编码原理。
2、 掌握PCM 编码信号的压缩与扩张的实现方式二、实验内容1、 设计一个PCM 调制系统的仿真模型2、 采用信号的压缩与扩张方式来提高信号的信噪比三、基本原理在现代通信系统中,以PCM (脉冲编码调制)为代表的编码调制技术被广泛地应用于模拟信号和数字传输中,所谓脉冲编码调制,就是将模拟信号的抽样量化值变换成代码,其编码方式如下图所示: m (t ) 抽样量化 信道低通滤波 m s (t ) m sq (t ) 噪声 编码 译码 m sq (t )m ‘s (t )PCM 编码经过抽样、量化、编码三个步骤将连续变化的模拟信号转换为数字编码。
为了便于用数字电路实现,其量化电平数一般为2的整数次幂,这样可以将模拟信号量化为二进制编码形式。
其量化方式可分为两种:均匀量化编码:常用二进制编码,主要有自然二进码和折叠二进码两种。
非均匀量化编码:常用13折线编码,它用8位折叠二进码来表示输入信号的抽样量化值,第一位表示量化值的极性,第二至第四位(段落码)的8种可能状态分别代表8个段落的起始电平,其它4位码(段内码)的16种状态用来分别代表每一段落的16个均匀划分的量化级。
通常情况下,我们采用信号压缩与扩张技术来实现非均匀量化,就是在保持信号固有的动态范围的前提下,在量化前将小信号放大,而将大信号进行压缩。
采用信号压缩后,用8位编码就可以表示均匀量化11位编码是才能表示的动态范围,这样能有效地提高校信号编码时的信噪比。
四、实验步骤在SystemVue 系统仿真软件中,系统提供了A 律和μ律两种标准的压缩气和扩张器,用户可以根据需要选取其中一种进行仿真实验。
1、设置一个均值为0,标准差为0.5的具有高斯分布的随机信号作为仿真用的模拟信号源。
2、在信号源的后方放置一个巴特沃思低通滤波器,设置其截止频率为10Hz,滤除高频分量。
3、在滤波器右侧放置一个A律13折线的压缩器(在通信库的Processors标签下),对信号进行压缩,并设定最大输入为1v。


模拟数字信号的传输学习目标:1、掌握低通信号和带通信号抽样定理;2、掌握PAM原理,自然抽样原理,半顶抽样原理及其脉冲振幅调判3、掌握模拟信号的量化原理,均匀量化,量化噪声,最化信噪比;非均匀量化,4、掌握PCM 原理及十三折线非均匀量化编码和PCM的抗噪声性能:。
5、了解△M,PPCM,及ADPCM原理6、理解PCM 与△M的系统的比较导言:通信系统可以分为模拟通信系统和数字通信系统两类,本章在介绍抽样定理和脉冲振幅调制的基础上,将着重讨论用来传输模拟语音信号常用的脉冲编码调制(PCM)和增量调制(ΔM)原理及性能,并简要介绍时分复用与多路数字电话系统原理的基本概念。
采用脉码调制的模拟信号数字传输系统如图1所示。
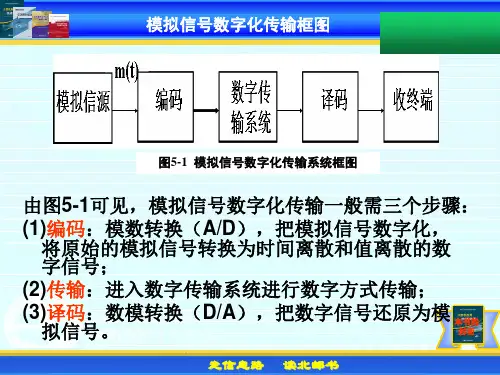
图1 模拟信号的数字传输在发送端把模拟信号转换为数字信号的过程简称为模数转换,通常用符号A/D表示。
简单地说,模数转换要经过抽样、量化和编码三个步骤。
其中抽样是把时间上连续的信号变成时间上离散的信号;量化是把抽样值在幅度进行离散化处理,使得量化后只有预定的Q个有限的值;编码是用一个M进制的代码表示量化后的抽样值,通常采用M=2的二进制代码来表示。
反过来在接收端把接收到的代码(数字信号)还原为模拟信号,这个过程简称为数模转换,通常用符号D/A表示。
数模转换是通过译码和低通滤波器完成的。
其中,译码是把代码变换为相应的量化值。
一、抽样定理抽样定理告诉我们:如果对某一带宽有限的时间连续信号(模拟信号)进行抽样,且抽速率达到一定数值时,那么根据这些抽样值就能准确地确定原信号。
也就是说,若要传输模拟信号,不一定要传输模拟信号本身,只需传输满足抽样定理要求的抽样值即可。
因此,该定理就为模拟信号的数字传输奠定了理论基础。
抽样定理的具体内容如下:一个频带限制在(0,)内的时间连续信号,如果以不大于1/(2)秒的间隔对它进行等间隔抽样,则将被所得到的抽样值完全确定。
也可以这么说:如果以的抽样速率进行均匀抽样上述信号,可以被所得到的抽样值完全确定。

电信模拟信号的数字传输引言电信模拟信号是指连续变化的信号,其数值在一定时间和幅度范围内连续变化,例如声波信号和视频信号。
然而,随着科技的进步和数字技术的发展,数字信号成为了主流。
数字信号通过将连续变化的模拟信号转换成离散的数字形式,使得信号的处理和传输更加稳定和可靠。
本文将介绍电信模拟信号通过数字传输的基本原理和常见方法。
模拟信号的数字化和样点化在数字传输中,首先需要对模拟信号进行数字化和样点化。
数字化是将连续的模拟信号转换为离散的数字信号,而样点化则是将连续信号在一定的时间间隔内进行采样。
数字化的过程中,一个常用的方法是使用模数转换器(ADC)。
ADC将连续的模拟信号按照一定的采样率进行采样,并将每个采样值转换为对应的数字表示。
采样率决定了取样的频率,通常以每秒采样次数(赫兹)来表示。
样点化是将连续信号在一定的时间间隔内进行采样,并将每个采样值表示为数字形式。
采样间隔决定了模拟信号在时间领域中离散化程度的密集程度。
常用的采样间隔是每秒采样次数(赫兹)的倒数。
数字信号的压缩和编码在模拟信号转换为数字信号后,接下来需要对数字信号进行压缩和编码。
压缩是指通过减少数字信号中的冗余信息来减小信号的数据量。
常用的压缩算法有无损压缩和有损压缩。
无损压缩保持信号的完整性,减小大小,但不会影响信号的质量。
而有损压缩则会牺牲一部分信号的质量来减小信号的数据量。
编码是将数字信号转换为特定的编码形式,以便在传输过程中进行解码。
常见的编码方法包括脉冲编码调制(PCM)和差分脉冲编码调制(DPCM)。
PCM将每个样本值按照一定的规则编码为固定长度的二进制数,而DPCM则根据当前样本值与前一样本值的差异来编码。
数字信号的传输和解码在数字信号的传输中,需要通过信道将数字信号从发送端传输到接收端。
由于信道存在噪声和其他干扰,可能会引起信号失真。
因此,传输过程中需要对信号进行调制和解调。
调制是将数字信号转换为适合传输的模拟信号。

模拟信号数字传输系统的主要功能模
块
模拟信号数字传输系统的主要功能模块包括以下几个部分:
1. 模拟信号调理:该模块负责对输入的模拟信号进行预处理,包括滤波、放大、衰减等操作,以确保信号的质量和可传输性。
2. 模数转换器(ADC):将模拟信号转换为数字信号的关键组件。
ADC 对输入的模拟信号进行采样,并将其量化成离散的数字值。
3. 数字信号处理:对数字信号进行处理和优化,以提高传输的效率和可靠性。
这可能包括滤波、纠错编码、数据压缩等操作。
4. 信道编码:在数字信号上添加冗余信息,以提高信号在传输过程中的抗干扰能力。
信道编码可以采用各种技术,如卷积编码、 Reed-Solomon 编码等。
5. 调制与解调:将数字信号调制到适合传输的载波上,以便在信道中传输。
在接收端,解调模块将接收到的已调信号解调成原始的数字信号。
6. 信道:实际传输数字信号的介质,可以是有线电缆、无线电磁波、光纤等。
7. 信道均衡:补偿信道对信号的影响,如衰减、延迟和相位失真等。
均衡器通过对接收信号进行处理,以恢复原始信号的特征。
8. 时钟恢复:从接收的数字信号中提取时钟信息,用于同步数据的采样和处理。
9. 数字信号解调:将接收到的数字信号解调成原始的数字数据。
10. 数模转换器(DAC):将数字信号转换回模拟信号,以便输出或进一步处理。
11. 模拟信号输出:将转换后的模拟信号输出到适当的设备或系统中。
这些功能模块协同工作,实现了模拟信号的数字传输和处理。
通过对信号进行数字化处理,可以提高传输的可靠性、降低噪声干扰,并实现更高效的数据传输。
第7章 模拟信号的数字传输7.1 学习指导 7.1.1 要点本章的要点主要有抽样定理;自然抽样和平顶抽样;均匀量化和非均匀量化;PCM 原理,A 律13折线编码,译码;ΔM 原理,不过载条件;PCM ,ΔM 系统的抗噪声性能;PCM 与ΔM 的比较;时分复用和多路数字电话系统原理;1. 概述为了使模拟信号实现数字化传输,首先要通过信源编码使模拟信号转换为数字信号,或称为―模/数转换‖即A/D 转换。
模/数转换的方法采用得最早而且应用较广泛的是脉冲编码调制(PCM),PCM 通信系统原理图如图7-1所示。
图7-1 PCM 通信系统原理图抽样量化器编码器模拟信号PCM 信号译码器低通滤波器模拟信号数字通信系统PCM 信号由图7-1可见,PCM 系统由以下三部分组成。
(1) 模/数转换(A/D 转换)模/数转换包括三个步骤:抽样(Sampling)、量化(Quantization)和编码(Coding)。
a. 抽样是把在时间上连续的模拟信号转换成时间上离散的抽样信号,抽样信号在时间上是离散的,但是其取值仍然是连续的,所以是离散模拟信号。
b. 量化。
量化是把幅度上连续的抽样信号转换成幅度离散的量化信号,故量化信号已经是数字信号了,它可以看成是多进制的数字脉冲信号。
c. 是编码。
编码是把时间离散且幅度离散的量化信号用一个二进制码组表示。
(2) 数字方式传输——基带传输或带通传输;(3) 数/模转换(D/A )——将数字信号还原为模拟信号。
包含了译码器和低通滤波器两部分。
2.抽样定理为模拟信号的数字化和时分多路复用(TDM )奠定了理论基础。
根据抽样的脉冲序列是冲激序列还是非冲激序列,抽样可以分为理想抽样和实际抽样。
抽样是按照一定的抽样速率,把时间上连续的模拟信号变成一系列时间上离散的抽样值的过程。
能否由此样值序列重建源信号,取决于抽样速率大小,而描述这一抽样速率条件的定理就是著名的抽样定理。
(1) 低通信号的抽样定理定理:设有一个频带限制在(0,f H )内的连续模拟信号m (t ),若以T s ≤1/(2f H )间隔对它抽样,则m (t )将被这些抽样值所完全确定。
第七章 模拟信号的数字传输数字通信系统中信道中传输的是数字信号。
但自然界中,有些信源是以模拟形式出现的,如话音、图像等。
因此在进行数字通信往往需先对信号(模拟的)数字化。
模拟信号数字化属信源编码范围,当然信源编码还包括并/串转换、加密和数据压缩。
本章重点讨论模拟信号数字化的基本方法,主要有PCM 、Δm 、ADPCM,还有其它VQ 、LPC 和CELP 。
模拟信号数字化的过程(得到数字信号)一般分三步:抽样、量化和编码。
其中“抽样”指抽取样值,抽取样点。
抽样的多少,快慢对通信的性能指标有决定影响。
抽样类似物理实验中实验曲线的描绘方法,测样点太少容易失真,;太多即费时又费力。
在通信中抽样点太少容易失真;太多时数据量大,传输时间长,效率低。
(带宽大,因Rb 大)。
如何抽样,由下面的抽样定理描述。
抽样定理是数字通信的基础。
下面引出定理,给出必要的证明,再说明其具体应用。
7.1抽样定理一 低通抽样定理1、定理描述频率受限于(0,H f )的时间连续信号m(t) ,若抽样频率s f 不小于2 H f ,则m(t)可被其抽样值s m (t) 完全确定。
(写完后解释,或强调两点)。
2、证明:s m (t)包含m(t)的全部信息;从s m (t)可无失真恢复m(t)。
抽样过程如图:T (t)m(t)(t)δ= s T 1M ()M()()2ωωδωπ=*T sn (t)(t nT )δδ∞=-∞=-∑ Tssn ()(n )δωωδωω∞=-∞=-∑s s s n m (t)m(nT )(t nT )δ∞=-∞=-∑ s sn s 1M ()M(n )T ωωω∞=-∞=-∑s m(t)=m (t)h(t)* s M()M ()H()ωωω=H H21,H(W)G ()0,ωωωω⎧≤⎪==⎨⎪⎩其它 H H H a H H sin t h(t)S (t)tωωωωππω== s H f 2f ≥ 时,得到的M()ω不失真。
抽样频率s f 不同时,s M ()ω的变化如图:ωωs Hf >2f s Hf =2f ω-s2ω-s2ω-HsaHs n m(t)m(nT )S (t nT )ωωπ∞=-∞=-∑ 内插公式3 说明1)抽样频率与奈奎斯特抽样频率 s H f 2f ≥,smin H f =2f s H1T 2f ≤smax H 1T 2f =2)理想抽样与实际抽样 以T (t)δ为抽样序列 3)低通带限信号的条件4)s H f =2f 的理解,H f 处的量为0,否则应大于2H f ,如正弦在H f 处的冲激强度取2Hf 可能正好全0,但纯正弦不用这样传,知道幅频即可。
4 应用与实例:1)用于电话质量的语音信号频率0.3~3.4KHz,s f 6.8KHz ≥,一般取8KHz(降低LPF 制作难度)。
2)声卡四种抽样频率,8KHz 为电话质量,11 KHz 为AM 广播质量,22 KHz 为FM 广播质量,44 KHz 为激光视盘(CD )质量。
1)带通信号的抽样 2)实际抽样3)抽样后的量化、编码方法。
二 带通抽样定理:1 描述:频率受限于(L f ,H f )的模拟信号m(t),其最小抽样频率满足:smin f =2B ,当H f nB =smin kf 2B(1)n=+,当H f nB kB =+, 0<k<1,H L B=f f -关于H f nB =证明见P191图。
)n2 应用:FDM 数字化,SBC ——子带编码7.2实际抽样前面抽样定理用的周期性冲激序列实际上不易产生,通常用窄脉冲串来完成抽样。
具体试验方法又分为下面两种:一自然抽样(曲顶)表达式:s P m (t)m(t)S (t)= s p 1M ()M()S ()2ωωωπ=* p s k S (t)A G (t kT )τ∞=-∞=-∑sss p s sn s nk s sk k 2A S ()Sa (k )T 22C (k )C T ss k A Sa()2T s1M ()T A Sa()2T ωωωωωτπτωδωωπδωωωττωωττ===--===∑∑()s s s sk A M ()Sa M(k )T 2ωττωωω=-∑()二 瞬时抽样(平顶)s s s s s sth(t)AD (t)Arect()H()A Sa()2m (t)A m(kT )D t kT A M ()Sa()M(k )T 2ττωτωτττωτωωω=====-∑∑(-)'s s s 'sm (t )m (k T )(t k T )M ()M (k )δωωω==-∑∑-Sa()2ωτ是随着ω变化的函数,使M()ω加权,称为孔径失真。
得到的s M ()ω使原频谱M()ω产生频率失真靠LPF 无法恢复。
所以,恢复模型变为:抽样化的信号为平顶,高度为抽样时刻的瞬时值。
比较三种抽样s m (t),s M ()ω及恢复方法。
抽样后,用LPF 恢复,平顶抽样有失真,需加“均衡网络”。
实际中平顶抽样应用多,T (t)δ与脉冲形成一起采用抽样保持电路实现采样保持。
抽样以后连续时间信号m(t)变成了时间离散的脉冲,脉冲幅度随窄带脉冲变化。
从调制的概念看,m(t)调制信号,抽样序列为窄脉冲。
所以,两种实际抽样的结果又称PAM信号。
三脉冲调制用基带信号(调制信号)去改变脉冲的某些参数,称为脉冲调制。
相应有PAM、PDM、PPM。
波形见P194PPM应用不多,PDM用于开关电源、单片机等,通信中有用的是PAM。
7.3 模拟信号的量化一概念:1 量化定义:用预先规定的有限个电平来表示模拟抽样值的过程,如下图m(t)——近似值2 量化信号qm(kT)——样值q S3 量化电平1q ,…M q q S i m (k T )q= 指量化器可能的输出电平,M 为量化电平数。
4 量化间隔i i 1v m m -=-(i 1m -,i m )为量化区间,i m 为量化区间端点。
5 量化误差q q n (t)m(t)m (t)=-只能减小(量化电平个数多一点),无法消除,也称量化噪声,大小由个数及方法决定。
6 量化噪声{}202q q E m(t)S N E [m(t)m (t)]⎡⎤⎢⎥⎣⎦=- 量化信噪比是量化器的主要性能指标之一。
它要求两个方面满足要求:后面看到PCM 系统抗噪声性能也主要由量化信噪比决定。
量化信噪比的大小与q m 的取法有关——即由量化方法决定。
先介绍最简单的。
7 过载量化噪声,当实际信号幅度超过量化范围时,称发生了过载,此时失真严重。
二 均匀量化:1 定义:把输入信号的取值域等距离分割,量化电平取各量化区间的中点。
2 量化信噪比qS N ,信号范围[a ,b],M 个量化电平, 则量化间隔b av M -=,量化电平i 1i 1i m m q 2-++= 第i 个量化区间终点:i m a i v =+ i vq a i v-2=+ 量化误差范围为v v -,22⎡⎤⎢⎥⎣⎦ 按0qS N 定义又分别求,()b 220x a S E m x f (x)d ⎡⎤==⎣⎦⎰()ii 1b 22q q q x aMbm 22i x i xam i 1N E m m (x-m )f (x)d (x-q )f (x)d (x-q )f (x)d -=⎡⎤=-=⎢⎥⎣⎦==⎰∑⎰⎰3 举例:一M 个量化电平的均匀量化器,其输入信号在区间[-a ,a]均匀分布,求量化信噪比。
解:22a220x a 1a M S xd (v)2a 312-===⎰ii 1Mm 2q i xm i=1M -a+i v 2x-a+(i-1)v i=13Mi 121N (x-q )d 2a v 1(x+a-i v+)d 22a (v)24(v)12-=====∑⎰∑⎰∑另外方法:q 2aq i x av 22v q n 221N (x q )d 2a1n d v(v)12--=-==⎰⎰20qS M N =,记住掌握,该结果对非均匀分布也适用,因M 很大时,在小区间内可认为均匀分布。
qN 0qS ()dB 20lg M N M=2S()dB=6N N =,N 增加1位,qS N 提高6dB 。
均匀量化有一个致命的缺点,就是不管信号幅度大小如何变化,其q N (t)始终不变,这导致信号小时0q S N 小,信号大时0q S N 大。
实际中小信号出现的概率相当多,导致0qSN 小。
要想提高qS N ,均匀量化只好提高M ,而M 大了,相应编码位数N 大,数据速率高,有效性低。
经验值,均匀量化要满足质量要求N=12位(220log N 20Nlg26N ==,要适应50dB 范围,即信号降低50dB 后,仍qS N 满足25dB 以上) 实际中常采用非均匀量化,大信号时间间隔大,小信号时间间隔小,使得qS N 趋于定值。
三 非均匀量化出发点是根据信号的不同区间来确定量化间隔,目的是改善小信号时的量化信噪比。
一般方法,先对信号抽样值进行压缩,再进行均匀量化。
即y=f(x) 非线性,对x 压缩,一般采用对数压缩y=lnx,但当x=0,y 无意义,再对y 均匀量化,收后再扩张。
1 对数压缩特性:实际广泛采用A 律, µ律(1) A 律压缩:中、欧采用A 律Ax y 1ln A =+,10<x A ≤(线性)1+lnAx y 1ln A =+, 1x 1A≤≤(对数) 其中A 取87.6,采用这种压缩后,qSN 改善明显。
但实际中 A 律压缩实现不容易,因为器件的非线性不易产生,且压缩与扩张又不好完全一致。
故实际上采用另一种折线法。
(2)日、北美采用µ律 2 扩线近似法:(1)13折线近似(A 律)方法:先把x 轴信号幅度作归一化处理(最大幅度值为1),然后把y 轴信号幅度作归一化处理。
X 轴:0~1范围 一分为二,中间点为1/2,取1/2~1之间为第八段 0~1/2范围 一分为二,中间点为1/4,取1/4~1/2为第七段 0~1/4范围 一分为二,中间点为1/8,取1/8~1/4为第六段 0~1/8范围 一分为二,中间点为1/16,取1/16~1/8为第五段 0~1/16范围 一分为二,中间点为1/32,取1/32~1/16为第四段 0~1/32范围 一分为二,中间点为1/64,取1/64~1/32为第三段 0~1/64范围 一分为二,中间点为1/128,取1/128~1/64为第二段 0~1/128范围 一分为二,中间点为0,取0~1/128为第一段而y 轴0~1均匀分为八段,一到八段为0~1/8,1/8~2/8,……将每个线段再均匀分为16个量化线(0~15),这样共有16*16=256个量化级(话音)。