激光原理第一章

第一章 光学谐振腔理论光学谐振腔是激光器不可缺少的组成部分。

它的作用是提供激光振荡所必需的负反馈，选择振荡模式，并且为激光输出腔外提供一定的耦合。

本章主要研究开放式光腔。

这类光学谐振腔通常由线度有限的两面光学反射镜相距一段距离共轴放置而形成。

与微波波段的封闭式谐振腔相比较，光学开腔敞开了侧面边界，以降低振荡的本征模式数目。

两面反射镜之间的轴向距离，称为腔长。

腔长远大于波长，也远大于反射镜的线度，一般为厘米或米的量级。

一面反射镜的反射率尽量接近１，以减小能量的损失，另一方面反射镜具有适当的透过率，以便能够输出一定的能量。

对于开腔式光腔的处理方法主要有两种，一种是建立在衍射理论基础上的，另一种是建立在几何理论基础上的。

为了对谐振腔理论有个较全面的理解，本章对那些不能用几何光学理论研究的谐振腔，则以方形对称共焦腔为例，采用衍射理论进行研究讨论，对于两面球面腔等，采用几何光学理论的处理方法，其中包括一些等效方法。

第一节 光学谐振腔概论如图1－1所示，考虑一个长、宽、高分别为l b a ,,矩形谐振腔中的本征模式，麦克斯韦方程的本征解的电场分量为：t i z t i y t i x p n m p n m p n m e z l p y b n x a m E t z y x E e z l p y b n x a m E t z y x E e z lp y b n x a m E t z y x E ,,,,,,sin cos sin ),,,(sin sin cos ),,,(cos sin sin ),,,(000ωωωπππππππππ---⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛= （1.1－1） 其中波矢z z y y x x e k e k e k k ++=，lp k b n k a m k z y x /,/,/πππ===（ ,3,2,1,0,,=p n m ），谐振角频率： ()()()222,,////l p b n a m ck c p n m πππω++== （1.1－2）（1．1．1）式表明在x ，y ，z 三个方向上，每一个本征模式的空间分布都是稳定的驻波分布，任意（m ，n ，p ）表征一种空间驻波分布。

激光原理与器件第一章激光的基本原理华南师范大学信息光电子科技学院教材与参考书周炳琨，“激光原理”，国防工业出版社俞宽新，“激光原理与激光技术”，北京工业大学出版社 伍长征，“激光物理学”复旦大学出版社激光的理论基础激光的发明激光的特性激光的应用一、激光的理论基础：爱因斯坦的受激辐射理论二、第一台激光器：1960年梅曼发明的红宝石激光器三、激光的特性：单色性好方向性好亮度高（或者说激光具有很高的梁子简并度）四、应用1、工业加工2、军事上的应用3、医学上的应用4、信息存储5、光通信6、科学研究工业应用医学美容航天军事测距，敌我识别，通信，制导科研光纤激光精密加工设备心血管支架的切割喷墨机喷嘴的打孔手机面板的切割§1相干性的光子概述光子的基本性质光波模式，光子态和相格光子的相干性光子的简并度一、光子——比电子更优越的信息载体，光子和电子的特性速度运动质量静止质量能量电子光子SJ h hv•×==−3410626.6ε2142022)(c m c p +=εkgm 31010109534.9−×=22c hv cm ==ε2201/cv m m −=sm c /1038×=cv <粒子参数光子的粒子属性（能量、动量、质量等）和波动属性（频率、波矢、偏振等）之间的联系在现代量子电动力学中得到解释。

hv=ε22chvcm ==εkn mc P h ==0ε：光子能量，v ：光波频率，m ：光子质量，：光子动量，P ：平面波矢。

k 任意电磁场可看作是一系列具有基元能量和基元动量的单色平面电磁波的线性叠加，或一系列电磁波的本征模式（或本征状态）的叠加。

二、光波模式、光子态、相格1、光波模式：在一个有边界条件限制的空间V内，具有特k定波矢的平面驻波。

（1）一维驻波的形成过程行波遇到障碍物后返回与原行波叠加。

tTx A y y y πλπ2cos 2cos 221=+=可以得到：一维驻波形成一维驻波须满足条件2λmx =Δ同理可得二维驻波的条件为：在x 、y 方向上满足公式αλcos /2mx =Δβλcos /2ny =Δ三维驻波2、波矢空间和几何空间在空腔为的立方体内，x 、y 、z 三个方向满足驻波条件。

第一章 激光的基本原理1. 为使He-Ne 激光器的相干长度达到1km ,它的单色性0/λλ∆应是多少? 提示: He-Ne 激光器输出中心波长632.8o nm λ= 解: 根据c λν=得 2cd d d d ννλνλλλ=-⇒=-则 ooνλνλ∆∆=再有 c c cL c τν==∆得106.32810o o o c o c c L L λλνλνν-∆∆====⨯ 2. 如果激光器和微波激射器分别在=10μm λ、=500nm λ和=3000MHz ν输出1W 连续功率，问每秒从激光上能级向下能级跃迁的粒子数是多少？解：设输出功率为P ，单位时间内从上能级向下能级跃迁的粒子数为n ，则：由此可得：其中346.62610J s h -=⨯⋅为普朗克常数，8310m/s c =⨯为真空中光速。

所以，将已知数据代入可得：=10μm λ时： 19-1=510s n ⨯=500nm λ时：18-1=2.510s n ⨯ =3000MHz ν时：23-1=510s n ⨯3．设一对激光能级为2E 和1E (21f f =)，相应的频率为ν(波长为λ)，能级上的粒子数密度分别为2n 和1n ，求(a) 当ν=3000MHz ，T=300K 时，21/?n n = (b) 当λ=1μm ，T=300K 时，21/?n n = (c) 当λ=1μm ，21/0.1n n =时，温度T=？解：当物质处于热平衡状态时，各能级上的粒子数服从玻尔兹曼统计分布,则(a) 当ν=3000MHz ，T=300K 时：(b) 当λ=1μm ，T=300K 时：cP nh nh νλ==PP n h hcλν==2211()exp exp exp b b b n E E h hc n k T k T k T νλ⎡⎤⎛⎫⎛⎫-=-=-=- ⎪ ⎪⎢⎥⎣⎦⎝⎭⎝⎭3492231 6.62610310exp 11.3810300n n --⎛⎫⨯⨯⨯=-≈ ⎪⨯⨯⎝⎭34822361 6.62610310exp 01.381010300n n ---⎛⎫⨯⨯⨯=-≈ ⎪⨯⨯⨯⎝⎭(c) 当λ=1μm ，21/0.1n n =时：4. 在红宝石调Q 激光器中，有可能将几乎全部3+r C 离子激发到激光上能级并产生激光巨脉冲。

激光原理考试重点激光原理考试重点第一章激光的基本原理1.光子的波动属性包括什么？动量与波矢的关系？光子的粒子属性包括什么？质量与频率的关系？答：光子的波动性包括频率，波矢，偏振等。

粒子性包括能量，动量，质量等。

动量与波矢：质量与频率：2.概念：相格、光子简并度。

答：在六维相空间中，一个光子态对应的相空间体积元为，上述相空间体积元称为相格。

处于同一光子态的光子数称为光子简并度，它具有以下几种相同含义：同态光子数、同一模式内的光子数、处于相干体积内的光子数、处于同一相格内的光子数3.光的自发辐射、受激辐射爱因斯坦系数的关系答：自发跃迁爱因斯坦系数：.受激吸收跃迁爱因斯坦系数：)。

受激辐射跃迁爱因斯坦系数：。

关系：;;为能级的统计权重(简并度)当时有4.形成稳定激光输出的两个充分条件是起振和稳定振荡。

形成激光的两个必要条件是粒子数反转分布和减少振荡模式数5.激光器由哪几部分组成？简要说明各部分的功能。

答：激光工作物质：用来实现粒子数反转和产生光的受激发射作用的物质体系。

接收来自泵浦源的能量，对外发射光波并能够强烈发光的活跃状态，也称为激活物质。

泵浦源：提供能量，实现工作物质的粒子数反转。

光学谐振腔：a)提供轴向光波模的正反馈；b)模式选择，保证激光器单模振荡，从而提高激光器的相干性。

6.自激振荡的条件？答：条件：其中为小信号增益系数：为包括放大器损耗和谐振腔损耗在内的平均损耗系数。

7.简述激光的特点？答：单色性，相干性，方向性和高亮度。

8.激光器分类：固体液体气体半导体染料第二章开放式光腔与高斯光束1.开放式谐振腔按照光束几何偏折损耗的高低，可以分为稳定腔、非稳腔、临界腔。

2.驻波条件，纵模频率间隔答：驻波条件：应满足等式：式中，为均匀平面波在腔内往返一周时的相位滞后；为光在真空中的波长；为腔的光学长度；为正整数。

相长干涉时与的关系为：或用频率来表示：.纵模频率间隔：不同的q值相应于不同的纵模。

腔的相邻两个纵模的频率之差3.光线在自由空间中行进距离L时所引起的坐标变换矩阵式什么？球面镜的对旁轴光线的变换矩阵？答：光线在自由空间中行进距离L时所引起的坐标变换矩阵式球面镜的对旁轴光线的变换矩阵：而为焦距。

第⼀章、激光的基本原理第⼀章、激光的基本原理1.为使He-Ne激光器的相⼲长度达到1km,它的单⾊性Δλ/λ0应是多少?2.设⼀对激光能级为E2和E1(f1=f2)，相应的频率为v(波长为λ)，能级上的粒⼦数密度分别为n2和n1，求：(a)当v=3000MHz，T=300K时，n2/n1=?(b)当λ=1µm，T=300K时，n2/n1=?(c)当λ=1µm，n2/n1=0.1时，温度T=?4.在红宝⽯Q调制激光器中，有可能将⼏乎全部Cr+3离⼦激发到激光上能级并产⽣激光巨脉冲。

设红宝⽯棒直径1cm，长度7.5cm，Cr+3离⼦浓度为2×1019cm-3，巨型脉冲宽度为10ns，求输出激光的最⼤能量和脉冲功率。

5试证明，由于⾃发辐射，原⼦在E2能级的平均寿命t s=1/A21。

8．（1）⼀质地均匀的材料对光的吸收系数为0.01mm-1，光通过10cm长的该材料后，出射光强为⼊射光强的百分之⼏？（2）⼀光束通过长度为1m的均匀激励的⼯作物质，如果出射光强是⼊射光强的两倍，试求该物质的增益系数。

第⼆章、开放式光腔与⾼斯光束1．试利⽤往返矩阵证明共焦腔为稳定腔，即任意傍轴光线在其中可以往返⽆限多次，⽽且两次往返即⾃⾏闭合。

2．试求平凹，双凹、凹凸共轴球⾯镜腔的稳定性条件。

6．试求出⽅形镜共焦腔⾯上的TEM30模的节线位置，这些节线是等距分布的吗？8．今有⼀球⾯腔，R1=1.5m，R2=-1m, L=80cm。

试证明该腔为稳定腔；求出它的等价共焦腔的参数；在图上画出等价共焦腔的具体位置。

13．某⼆氧化碳激光器,采⽤平-凹腔，凹⾯镜的R=2m，腔长L=1m。

试给出它所产⽣的⾼斯光束的束腰斑半径ω0的⼤⼩与位置、该⾼斯光束的f及θ0的⼤⼩。

16．某⾼斯光束ω0=1.2mm，λ=10.6µm。

今⽤F=2cm的锗透镜来聚焦，当束腰与透镜的距离为10m、1m、10cm、0时求焦斑⼤⼩和位置，并分析所得的结果。

第一章 激光的基本原理及其特性激光技术是二十世纪六十年代初发展起来的一门新兴学科。

激光的问世引起了现代光学技术的巨大变革。

激光在现代工业、农业、医学、通讯、国防、科学研究等各方面的应用迅速扩展，之所以在短期间获得如此大的发展是和它本身的特点分不开的。

激光与普通光源相比较有三个主要特点，即方向性好，相干性好和亮度高，其原因在于激光主要是光的受激辐射，而普通光源主要是光的自发辐射。

研究激光原理就是要研究光的受激辐射是如何在激光器内产生并占据主导地位而抑制自发辐射的。

本章首先从光的辐射原理讲起，讨论与激光的发明和激光技术的发展有关的各方面物理基础和产生激光的条件。

光的辐射既是一种电磁波又是一种粒子流，激光是在人们认识到光有这两种相互对立而又相互联系的性质后才发明的。

因此本章从介绍光的波粒二象性开始研究原子的辐射跃迁。

激光的产生又是光与物质的相互作用的结果，对光的平衡热辐射和光与物质的相互作用 (光的自发辐射、受激辐射、受激吸收) 的研究是发明激光的物理基础。

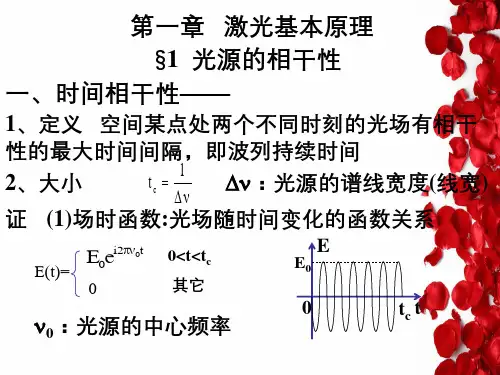
光谱线的宽度，线型函数是影响激光器性能的重要因素，提高激光的单色性是激光技术的发展的一个重要方向。

阐明上述这些基础后，本章最后一节讨论激光产生的条件。

1. 1 激光的特性光的一个基本性质就是具有波粒二象性。

人类对光的认识经历了牛顿的微粒说、惠更斯菲涅耳的波动说到爱因斯坦的光子说的发展，最后才认识到波动性和粒子性是光的客观属性，波动性和粒子性总是同时存在的。

一方面光是电磁波，具有波动的性质，有一定的频率和波长。

另一方面光是光子流，光子是具有一定能量和动量的物质粒子。

在—定条件下，可能某一方面的属性比较明显，而当条件改变后，另一方面的属性变得更为明显。

例如，光在传播过程中所表现的干涉、衍射等现象中其波动性较为明显，这时往往可以把光看作是由一列一列的光波组成的；而当光和实物互相作用时(例如光的吸收、发射、光电效应等)，其粒子性较为明显，这时往往又把光看作是由一个一个光子组成的光子流。