小学奥数勾股定理

小学数学人教新版六年级上册实用资料勾股定理内容概述1.勾股定理(毕达哥拉斯定理):直角三角形中的两直角边平方后的和等于斜边的平方．公元前500年古希腊的毕达哥拉斯发现了勾股定理后,曾宰牛百头,广设盛筵以示庆贺．2. 公元前11世纪的《周髀算经》中提到:故折矩,以为句广三,股修四、径修五．既方之.外半卿一矩,环而共盘.得成三、四、五．三国时期的赵爽注解道:句股各自乘,并之为弦实,开方除之,即弦.案:弦图又可以句股相乘为朱实二,倍之为朱实四,以句股之差自相乘为中黄实,加差之,亦成弦实．汉朝张苍、狄昌寿整理的《九章算术》第九卷为《句股》.其中解释到:短面曰句，长面曰股，相与结角曰弦.句短其股，股短其弦．句股各自乘，并，而开方除之，即弦．中国科学院数学与系统科学研究院的徽标(右图所示)采用的就是赵爽的弦图.2002年在北京举行的国际数学家大会的徽标也是弦图．如下,在弦图中有EFGH S =四边形()12ABCD MNPQ S S +矩形矩形C DG ADG CDE S S S '==V V V3. 伽菲尔德证法:美国第20任总统伽菲尔德对数学有浓厚的兴趣,在还是中学教师时曾给出一种勾股定理的证明方法：梯形面积=12(上底＋下底)×高 =12(a+b)×(a+b) =12(a+b)2；三个直角三角形的面积和=12ab+12ab+12c 2； 梯形面积=三个直角三角形面积和．12(a+b)2=12ab+12ab+12c 2,所以a 2+b 2=c 2. 4.公元前3世纪的欧几里得在《几何原本》中给出一种证明,简叙如下：如图,作出三个正方形,它们的边长分别为直角三角形ABC 的三边长.连接图中的虚线段对应的点；过C 作CK 平行于AF,交AB 、FG 分别于J 、K 点．易证△AFC ≌△BAE ,有12FAC S =V AF.FK=12AFKJ S 矩形,12BAE S =V EA.CA=ACDE S 正方形,所以AFKJ S =矩形ACDE S 正方形；易证△C BG ≌△HBA，有12CBG S =V BG.KG=12KGBJ S 矩形,12HBA S =V BH.IH=CBHI S 正方形,所以KGBJ S 矩形CBHI S =正方形.而AFGB AFKJ S S =正方形矩形KGBJ ACBE S S +=矩形正方形CBHI S +正方形．即有AB 2=AC 2+CB 2.5. 勾股数组:a=u 2-v 2,b=2uv,c=u 2+v 2如果a 、6、c 可以如此表达,那么a 、b 、c 称之为勾股数组,有a 2+b 2=c 2．如:u=2,v=l 时a=3,b=4,c=5；u=7,v=6时a=13,b=84,c=85．当然将已知的勾股数组内每个数都同时扩大若干倍得到的新的一组数还是勾股数组.典型问题2.智能机器猫从平面上的O 点出发.按下列规律行走:由O 向东走12厘米到A 1,由A 1向北走24厘米到A 2,由A 2向西走36厘米到A 3,由A 3向南走48厘米到A 4,由A 4向东走60厘米到A 5,…,问:智能机器猫到达A 6点与O 点的距离是多少厘米?【分析与解】 如右图所示,当智能机器猫到达A 6点时,相对 O 点,向东走了12-36+60=36厘米,向北走了24-48+72=48厘米． 有26OA =362+482,即OA 2=60．所以,A 6点到O 点的距离为60厘米．4.如图32-3所示,直角三角形PQR 的两个直角边分别为5厘米,9厘米问下图中3个正方形面积之和比4个三角形面积之和大多少?【分析与解】 如右图,延长AR,DQ,过E,F 分别作AR,DQ 的平行线,在正方形EFRQ 内交成四个全等的直角三角形和一个小正方形GHMN ，四个全等的直角三角形面积之和与四个白色的三角形面积之和相等．小正方形HGNM 的边长为9-5=4厘米,所以面积为16平方厘米,而另 外两个正方形ABPR 、CDQR 他的面积分别为25,81．所以原图中3个正方 形面积之和比4个三角形面积之和大25+8l+16=122平方厘米．6.若把边长为1的正方形ABCD 的四个角剪掉,得一四边形A 1B l C l D l ,试问怎样剪,才能使剩下的图形仍为正方形,且剩下图形的面积为原来正方形面积的59,请说明理由.(写出证明及计算过程)【分析与解】如左图所示,我们知道利用弦图,可是弦图怎么利用?设构造出的弦图中最小正方形的面积为x最大正方形面积为1,那么有剩下的正方形面积为12(x+1)=59,所以x=19.那么,最小正方形的边长为13.由于是四角对称的剪去,所以有AD l=DC l=CB l=BA1=13,AA l=BB l=CC l=DD l=23证明及计算过程略．8.有5个长方形,它们的长和宽都是整数,且5个长和5个宽恰好是1～10这10个整数；现在用这5个长方形拼成1个大正方形,那么,大正方形面积的最小值为多少?【分析与解】注意到,5个长、宽均不相等的长方形拼成一个正方形,只有一种拼法.(如右图所示，由弦图联想到)．A、B、C、D中必有一个长方形的一边长为10,不妨设为A，那么显然不能组成边长为10的正方形；如果能够组成边长为11的正方形,那么有11=10+1=9+2=8+3=7+4=6+5,那么大正方形的四边必须是为11,则剩下的两个数,它们的和为11,为中问阴影部分的长、宽和；评注:如果能够组成边长为12的正方形,那么有12=10+2=9+3=8+4=7+5,剩下1、6试填不满足．对于边长为13的正方形,注意到13=10+3=9+4=8+5=7+6,剩下1、2,有见下图情形,满足．10.园林小路,曲径通幽.如图32-7所示,小路由白色正方形石板和青、红两色的三角形石板铺成.问：内圈三角形石板的总面积大,还是外圈三角形的总面积大?请说明理由．【分析与解】如图①,我们任意抽出两块相邻的白色正方形石板,及它们所夹成的青、红两色的三角形石板，如图②所示.图中有∠CDB+∠ADG=1800.如果③,将△CDE 逆时针旋转900,得△C DG '.有A 、D 、C '在同一条直线上,且△C DG '与△ADG 等底同高,所以有C DG ADG CDE S S S '==V V V .也就是说,任意两块相邻的白色正方形石板,它们所夹成的青色三角形与红色三角形面积相等．注意到在原图中,除了外圈青色的两块三角形外,外圈三角形、内圈三角形一一对应.所以原图中,外圈三角形的面积大于内圈三角形的面积,如图①所示．。

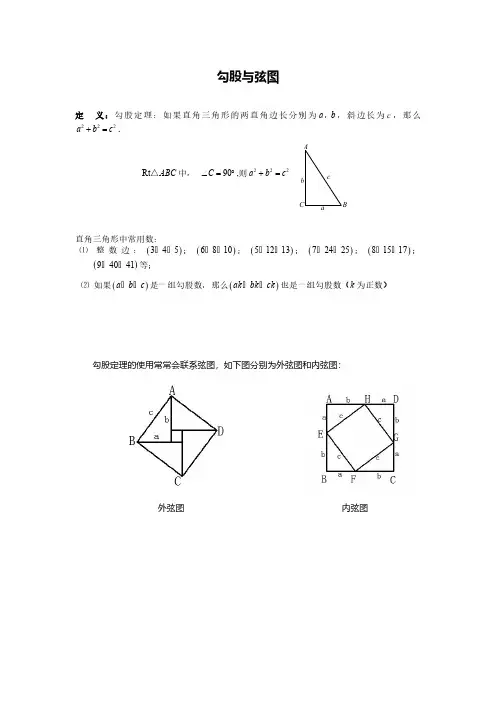
勾股与弦图定 义：勾股定理：如果直角三角形的两直角边长分别为，斜边长为，那么a b ，c ．222a b c +=中， ,则Rt ABC △90C ∠=︒222a b c +=直角三角形中常用数：⑴ 整数边：；；；；；()345，，()6810，，()51213，，()72425，，()81517，，等；()94041，，⑵ 如果是一组勾股数，那么也是一组勾股数（k 为正数） ()a b c ，，()ak bk ck ，，勾股定理的使用常常会联系弦图，如下图分别为外弦图和内弦图：外弦图内弦图cba C B A【例1】如图，要将楼梯铺上地毯，则需要 米的地毯．【例2】如图，以三角形ABC的三边为边长向外作三个正方形，正方形内的数代表正方形的面积，求未知正方形的面积.【例3】如图，是由一个直角边都是1的直角三角形向外作直角三角形得到，形成一个美丽的螺旋图案，第8个直角三角形的斜边是多少？【例4】如图所示，三角形都是直角三角形，四边形都是正方形，最大正方形的边长是7，问：除最大正方形外的所有正方形的面积之和是多少？【例5】如图，直线l上有三个正方形a，b，c，若a，c的面积分别为5和11，则b的面积为 ．【例6】下图是学校一个正方形花圃的设计图，图中阴影部分是花圃，空白部分是草坪。

求花圃的面积是多少平方米？【例7】 如图，是由四个完全相同的长方形拼成，大正方形的面积是100平方分米，小正方形的面积是16平方分米，则每个长方形的面积是多少平方分米，长方形的短边是多少分米？【例8】如图，CDEF 是正方形，ABCD 是等腰梯形，它的上底AD=23厘米，下底BC=35厘米，求三角形ADE 的面积.【例9】如下图所示，两个正方形ABCD 和DEFG 的边长都是整数厘米，点E 在线段CD 上，且CE<DE,线段CF=5厘米，则五边形ABCFG 的面积等于多少平方厘米？FGDECB A【例10】如下图所示，一个边长为10厘米的正方形木板斜靠在墙角上（木板厚度不计），AO距离为8厘米，那么点C距离地面的高度是多少厘米？。

奥数实用技巧直角三角形求解奥数实用技巧：直角三角形求解直角三角形是数学中常见的一种特殊三角形，它具有一个90度的直角和两条相对边长不等的直角边。

在解题时，我们经常需要利用一些实用技巧来求解直角三角形的边长、角度和面积。

以下是一些常用的奥数实用技巧，帮助我们更高效地解决与直角三角形相关的问题。

1. 勾股定理勾股定理是解决直角三角形问题的基础，它可以表示为a²+ b²= c²，其中a和b为直角三角形的两条直角边，c为斜边。

当已知两条直角边的长度时，可以直接利用勾股定理求解斜边的长度。

例题1：已知直角三角形的直角边长分别为3和4，求斜边的长度。

解: 根据勾股定理，可以得到3² + 4² = c²，即9 + 16 = c²。

计算可得c² = 25，因此c = 5。

所以斜边的长度为5。

2. 正弦定理和余弦定理正弦定理和余弦定理是求解三角形内角度和边长的准则。

正弦定理可以表示为：a/sinA = b/sinB = c/sinC，其中a、b和c分别为三角形的边长，A、B和C为对应的内角。

余弦定理可以表示为：c² = a² + b² - 2abcosC，其中c为三角形的斜边，a和b为直角边。

根据正弦定理和余弦定理，我们可以求解直角三角形的各个角度和边长。

例题2：已知直角三角形的一条直角边为5，斜边为13，求另一条直角边的长度。

解：根据勾股定理，可以求得另一条直角边的长度为√(13² - 5²) = 12。

例题3：已知直角三角形的两条直角边的长度分别为3和4，求斜边的长度和三个内角的大小。

解：根据勾股定理，可以求得斜边的长度为5。

然后，利用正弦定理可以求得三个内角：sinA = 3/5，A = arcsin(3/5) ≈ 36.87°；sinB = 4/5，B = arcsin(4/5) ≈ 53.13°；由于直角为90°，所以C = 90°。

【培优奥数专题】五年级下册数学-勾股定理（解析版）一、知识点1、历史三千多年前，周朝数学家商高提出“勾三股四弦五”最早由公元前3世纪中我汉代数学家赵爽在《周髀算经》注解时给出相传，公元前550年，古希腊毕达哥拉斯首先发现，但其证明方法已失传2、概念直角三角形两直角边的平方之和等于斜边的平方例如：两直角边的长度分别为a和b，斜边的长度为c，则a²＋b²＝c²3、勾股数组概念：指满足算式a²＋b²＝c²的三个正整数常见的勾股数组：（3，4，5）、（5，12，13）、（7，24，25）、（8，15，17）变形的勾股数组：将上面四组勾股数组中任意一组的三个数同时扩大或缩小相同的倍数之后仍然是勾股数组4、勾股定理的逆定理如果一个三角形的三边长a、b、c满足a²＋b²＝c²，那么这个三角形是直角三角形二、学习目标1.我能够了解勾股定理的概念。

2.我能够理解勾股定理的逆定理，并能准确判断一个三角形是否为直角三角形。

3.我能够运用勾股定理解决简单的实际问题。

三、课前练习1.计算下列各题，并牢牢记住答案。

11²＝12²＝13²＝14²＝15²＝16²＝17²＝18²＝19²＝20²＝21²＝22²＝23²＝24²＝25²＝【解答】1211441691962252562893243614004414845295766252.画出下面图形的对称轴，并说一说你有什么发现？【解答】略四、典型例题思路点拨如何判断三角形为直角三角形如果三角形两条边的平方和等于第三边的平方，那么这个三角形就是直角三角形。

最长边所对的角为直角。

例题11.下列各组数中能恰好作为直角三角形三边长的是。

A.（4，5，6）B.（16，12，10）C.（10，24，26）D.（5，14，17）【解答】根据两条边的平方和等于第三边的平方，那么这个三角形就是直角三角形发现只有C符合10²＋24²＝26²。

勾股定理：直角三角形两直角边（即“勾”，“股”）边长平方和等于斜边（即“弦”）边长的平方。

也就是说，设直角三角形两直角边为a和b,斜边为c,那么a2+b2=c2o勾膻定理勾股数★满足关系a2+b2=c2的3个正整数a,b,c称为勾股数。

★常见的勾股数有：①3,4,5；②6,8,10；③8,15,17:④7,24,25；⑤5,12,13；⑥9,12,15…注意：①3,4,5既是勾股数，又是三个连续整数，它们非常特殊，不要认为三个连续整数都是勾股数；②每组勾股数的相同倍数也是勾股数；（如：3,4,5；6,8,10；9,12,15）③勾股数必须都是正整数，（如：0.3,0.4,0.5都是小数，因而不是勾股数）3米例2、一棵大树在离地面3米处折断，树的顶端落在离树的底部4米处，那么这棵树折断之前的高度是多少米？巩固、如图为某楼梯，测得楼梯的长为5米，高3米，计划在楼梯表面铺地毯，地毯的长度至少需要多少米？巩固、飞机在空中水平飞行，某一时刻刚好飞到一个站着不动的女孩头顶正上方4000m 处,过了20秒，飞机距离这个女孩头顶5000m,则飞机速度是多少？例3、暑假中，小明和同学们到某海岛去探宝旅游，按照如图所示的路线探宝.他们登陆后先往东走8km，又往北走2km，遇到障碍后又往西走3km，再折向北走6km处往东一拐，仅走1km就找到了宝藏，则登陆点到埋宝藏点的直线距离为km.丄埋宝藏点632登陆点8巩固、轮船从海中岛A出发，先向北航行9km，又往西航行9km，由于遇到冰山，只好又向南航行4km，再向西航行6km，再折向北航行2km，最后又向西航行9km，到达目的地B,求AB 两地间的距离.例4、一个圆桶，底面直径为24cm，高32cm，则桶内所能容下的最长木棒为多少厘米?如图，是一个三级台阶，它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶两相对的端点，A点有一只昆虫想到B点去吃可口的食物，则昆虫沿着台阶爬到B点的最短路程是分米？B例5、下图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A,B，C,D的边长分别是3,5,2,3,则最大正方形E的面积是？巩固、如图所示，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积的和是cm2.巩固、如图所示，阴影部分是一个正方形，则此正方形的面积为?例6、如图，已知直角三角形两直角边BC，AC的长分别为3cm和4cm,那么CD有多长?巩固、三角形的三边长分别为6,&10，它的最短边上的高为，最长边上的高为巩固、若直角三角形的三边长分别为X,6,8,则X2=例7、等腰三角形ABC的腰长为10,底边上的高为6,则底边的长为多少？巩固、如图，一根12米高的电线杆两侧各用15米的铁丝固定，两个固定点之间的距离是。

小学五年级奥数之勾股定理（1）勾股定理：一个直角三角形中，构成直角的两边叫做直角边；直角所对的边叫做斜边。

直角边的平方和等于斜边的平方。

设直角边为a和b，斜边为c，那么有：a²+b²=c²。

其中斜边是直角三角形中最长的边。

一般∠A对应的边是a，∠B对应的边是b，∠C 对应的边是c。

中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦，所以称这个定理为勾股定理。

一、基础训练1、在直角三角形ABC中，∠C=90度，如果a=6、b=8,那么c=（）；2、在直角三角形中，∠C=90度，如果a=5，c=13，那么b=（）；3、在直角三角形中，∠c=90度，如果c=625，b=20，求a=（）；4、以下各组数为边长，可以构成直角三角形的是（）。

A 6、7、8B 8、10、12C 10 24 26 D、20 、15、6245、一个直角三角形的一条直角边是12厘米，斜边是13厘米，问这个直角三角形的面积是多少平方厘米？6、下面正方形ABCD中，∠BAD=90°，∠CBD=90°，AD=8厘米、AB=6厘米,BC=20厘米，问正方形ABCD的面积是多少平方厘米？7、下面大正方形ABCD中，由4个一样的直角三角形和一个小正方形拼成，其中AF=3厘米、CE=7厘米,大正方形ABCD的面积是多少平方厘米？小正方形的面积是多少平方厘米？8、如图，四边形ABCD，EFGH，NHMC都是正方形，边长分别是a、b、c;A、B、N、E、F五点在同一直线上，则正方形CNHM的面积是多少?单位：厘米)，用含有a、b、c、d的字母来表示。

9、如图，正方形网状格子组成的图中，AB、CD、EF、GH四条线段，其中可以构成直角三角形的三边的线段是（）?10、一个圆拄形的杯子中放着一根吸管，最多可以露出4厘米，最少可以露出2厘米，这个吸管的长度是12厘米，问玻璃杯底面直径是多少厘米？11、一根绳子在一个圆柱上从一端到另外一端绕了4整圈，如下图所示，圆柱底面周长4米，长12米，你可以算出绳子的长度吗？12、右图是美丽的人造平面珊瑚礁图案。

勾股定理学前需掌握：三角形和多边形的面积计算方法有开平方和求平方根的概念了解为什么学习勾股定理？有一定图形和数字结合的认识为什么要学习勾股定理？勾股定理呢是几何的基础.首先,三角形是多边形中最简单的,而直角三角形是三角形中特殊的一种，这是数与形结合的最初形式。

.学习了勾股定理,就会解直角三角形.很多时候,在普通的三角形里,也会作辅助线分成几个直角三角形来做.所以,这个很基础!几何学是研究空间关系的数学分支，有时简称为几何。

学过数学的人，都知道它有一门分科叫作“几何学”，然而却不一定知道“几何”这个名称是怎么来的。

在中国古代，这门数学分科并不叫“几何”，而是叫作“形学”。

“几何”二字，在中文里原先也不是一个数学专有名词，而是个虚词，意思是“多少”。

比如三国时曹操那首著名的《短歌行》诗，有这么两句：“对酒当歌，人生几何？”这里的“几何”就是多少的意思。

那么，是谁首先把“几何”一词作为数学的专业名词来使用的，用它来称呼这门数学分科的呢？这是明末杰出的科学家徐光启。

关于勾股定理勾股定理是几何学中的明珠，所以它充满魅力，千百年来，人们对它的证明趋之若骛，其中有著名的数学家，也有业余数学爱好者，有普通的老百姓，也有尊贵的政要权贵，甚至有国家总统。

也许是因为勾股定理既重要又简单，更容易吸引人，才使它成百次地反复被人炒作，反复被人论证。

1940年出版过一本名为《毕达哥拉斯命题》的勾股定理的证明专辑，其中收集了367种不同的证明方法。

实际上还不止于此，有资料表明，关于勾股定理的证明方法已有500余种，仅我国清末数学家华蘅芳就提供了二十多种精彩的证法。

这是任何定理无法比拟的。

在这数百种证明方法中，有的十分精彩，有的十分简洁，有的因为证明者身份的特殊而非常著名。

在国外，尤其在西方，勾股定理通常被称为毕达哥拉斯定理．这是由于，他们认为最早发现直角三角形具有“勾2+股2=弦2”这一性质并且最先给出严格证明的是古希腊的数学家毕达哥拉斯（Pythagoras，约公元前580－公元前500）．实际上，在更早期的人类活动中，人们就已经认识到这一定理的某些特例．除我国在公元前1000多年前发现勾股定理外，据说古埃及人也曾利用“勾三股四弦五”的法则来确定直角．但是，这一传说引起过许多数学史家的怀疑．比如，美国的数学史家M·克莱因教授曾经指出：“我们也不知道埃及人是否认识到毕达哥拉斯定理．我们知道他们有拉绳人（测量员），但所传他们在绳上打结，把全长分成长度为3、4、5的三段，然后用来形成直角三角形之说，则从未在任何文件上得到证实．”不过，考古学家们发现了几块大约完成于公元前2000年左右的古巴比伦的泥版书，据专家们考证，其中一块上面刻有如下问题：“一根长度为30个单位的棍子直立在墙上，当其上端滑下6个单位时，请问其下端离开墙角有多远？”这是一个三边为3:4:5三角形的特殊例子；专家们还发现，在另一块版板上面刻着一个奇特的数表，表中共刻有四列十五行数字，这是一个勾股数表：最右边一列为从1到15的序号，而左边三列则分别是股、勾、弦的数值，一共记载着15组勾股数．这说明，勾股定理实际上早已进入了人类知识的宝库．证明方法：先拿四个一样的直角三角形。

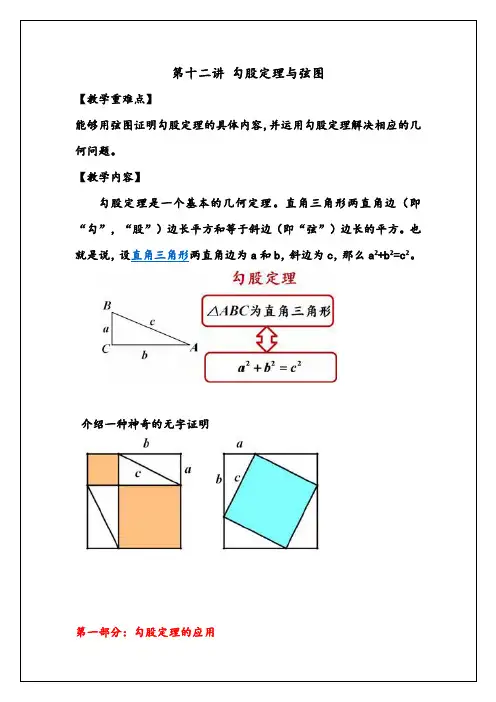
的面积。

⑴大正方形边长为：a＋b
⑵小正方形边长为：a－b
米，求这个三角形的面积？
【例 7】(★★★★★)
从一块正方形玻璃上裁下宽为16 分米的一长方形条后，剩下的那块长方形的面积为336 平方分米，原来正方形的面积是多少平方分米？
自我检测
1.将长为10 米的梯子斜靠在墙上，若梯子上端到墙的底端距离为6
米，则梯足到墙的底端距离为__________米．
2.若直角三角形一直角边和斜边分别为17 和145 ，则另一直角边
为___________。

3.已知一个直角三角形的两边长分别为3 和4，则第三边长的平方
是。

4.如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7 cm,则正方形A,B,C,D的面积之和为
___________cm2．
5.如图在△ABC中，AB =15,AC=13,高AD=12，则△ABC的面积为？
易错题
（1）某人以匀速行走在一条公路上，公路两端的车站每隔相同的时间开出一辆公共汽车，该行人发现每隔30分钟就会有一辆公共汽车追上他；而每隔20分钟有一辆公共汽车迎面开来．问车站每隔多少分钟开出一辆车？
（2）有4袋糖块，其中任意3袋的总块数都超过90。

这4袋糖块总共最少有多少块？。

勾股定理一、内容提要 1.勾股定理及逆定理：△ABC 中 ∠C ＝Rt ∠⇔a 2＋b 2=c 2 2. 勾股定理及逆定理的应用① 作已知线段a 的2，3，5……倍② 计算图形的长度，面积，并用计算方法解几何题 ③ 证明线段的平方关系等。

3. 勾股数的定义：如果三个正整数a,b,c 满足等式a 2＋b 2=c 2，那么这三个正整数a,b,c 叫做一组勾股数.4. 勾股数的推算公式① 罗士琳法则（罗士琳是我国清代的数学家1789――1853）任取两个正整数m 和n(m>n),那么m 2-n 2，2mn, m 2+n 2是一组勾股数。

② 如果k 是大于1的奇数，那么k, 212-k ,212+k 是一组勾股数。

③ 如果k 是大于2的偶数，那么k, 122-⎪⎭⎫ ⎝⎛K ,122+⎪⎭⎫⎝⎛K 是一组勾股数。

④ 如果a,b,c 是勾股数，那么na, nb, nc (n 是正整数)也是勾股数。

5. 熟悉勾股数可提高计算速度，顺利地判定直角三角形。

简单的勾股数有：3，4，5； 5，12，13； 7，24，25； 8，15，17； 9，40，41。

1.常用勾股数口诀记忆常见勾股数3，4，5 ： 勾三股四弦五 5，12，13 ： 5·12记一生 6，8，10： 连续的偶数 7，24，25 ： 企鹅是二百五 8，15，17 ： 八月十五在一起 特殊勾股数连续的勾股数只有3，4，5连续的偶数勾股数只有6，8，102.100以内的勾股数 开头数字为20以内6. 3 4 5；5 12 13； 6 8 10；7 24 25；8 15 17；9 12 15；9 40 41；10 24 26；11 60 61；12 16 20；12 35 37；13 84 85；14 48 50；15 20 25；15 36 39；16 30 34；16 63 65；18 24 30；18 80 82二、例题例1.已知线段a a5a 2a 3a 5a求作线段5a a分析一：5a ＝25a ＝224a a + 2a∴5a 是以2a 和a 为两条直角边的直角三角形的斜边。

【导语】天⾼鸟飞，海阔鱼跃，学习这舞台，秀出你独特的精彩⽤好分秒时间，积累点滴知识，解决疑难问题，学会举⼀反三。

以下是为⼤家整理的《⼩学奥数勾股定理与弦图练习及答案【三篇】》供您查阅。

【第⼀篇】
例2、△ABC是直⾓三⾓形，在边AB、BC、CA上分别取点D、E、F，使得AD=AF=FC=EC。

当△DEF成为等腰直⾓三⾓形、BE=3cm、DB=1cm时，求△ABC的⾯积。

【第⼆篇】
例1、如图，P是正⽅形ABCD外⾯的⼀点，PB=12厘⽶，△APB的⾯积是90平⽅厘⽶，△CPB的⾯积是48平⽅厘⽶。

请问：正⽅形ABCD的⾯积是多少平⽅厘⽶？
【第三篇】
习题：从⼀个正⽅形的⽊板上锯下宽0.5⽶的⼀个长⽅形⽊条以后，剩下的长⽅形⾯积为5平⽅⽶，问：锯下的长⽅形⽊条的⾯积等于多少平⽅⽶？。

14证明：在FD的延长线上取点G，使GD＝FD，连接EG、BG∵∠A＝90∴∠ABC+∠C＝90∵D是BC的中点∴BD＝CD∵GD＝FD，∠BDG＝∠CDF∴△BDG≌△CDF （SAS）∴BG＝CF，∠GBD＝∠C∴∠ABG＝∠ABC+∠GBD＝∠ABC+∠C＝90∴EG²=BE²+BG²∴EG²=BE²+CF²∵DE⊥DF，GD＝FD∴DE垂直平分FG∴EF＝EG∴EF²=BE²+CF²15作CD=CE，且角BDC=角ACE，连BD,DF，如图所示。

因为AC=AB,CE=CD所以三角形AEC全等于三角形BDC所以 AE=BD角BCD=角ACE角CAB=角CBD因为角CAB+角CBA=90度所以角CBD+角CBA=90度所以 BD垂直于BF因为角BCF+角ACE=45度且角ACE=角BCD所以角BCD+角BCF=45度所以角DCF=角ECF=45度又CE=CD CF=CF所以三角形CEF全等于三角形CDF所以EF=DF在直角三角形BDF中因为 BD平方+BF平方=DF平方又 BD=AE,EF=DF所以 AE平方+BF平方=EF平方12 作AD⊥BC于DPA^2=PD^2+AD^2∵AD^2=AB^2-BD^2∴PA^2=PD^2+AB^2-BD^2∴PA^2=AB^2-(BD+PD)(BD-PD)=AB^2-PC·BP∴PA^2+PC·BP=AB^2=2510 证明：在FD的延长线上取点G，使GD＝FD，连接EG、BG ∵∠A＝90∴∠ABC+∠C＝90∵D是BC的中点∴BD＝CD∵GD＝FD，∠BDG＝∠CDF∴△BDG≌△CDF （SAS）∴BG＝CF，∠GBD＝∠C∴∠ABG＝∠ABC+∠GBD＝∠ABC+∠C＝90∴EG²=BE²+BG²∴EG²=BE²+CF²∵DE⊥DF，GD＝FD∴DE垂直平分FG∴EF＝EG∴EF²=BE²+CF²8 延长AD到点E，使DE=AD=6，连接CE∵BD=CD，AD=DE，∠ADB=∠CDE∴△ABD≌△CED∴CE=AB=5∵AE=12，CE=5，AC=13∴CE²+AE²=AC²∴∠E=90°∴CD²=5²+6²=61∴CD=√61∴BC=2√6113由勾股定理可得：AP^2= AH^2+PH^2=AE^2+PE^2BP^2= BE^2+PE^2=BF^2+PF^2CP^2= CF^2+PF^2=CG^2+PG^2DP^2= DG^2+PG^2=DH^2+PH^2以上四式后一等号两边分别相加，并代入已知数值可得: 9+BE^2+36+1=AE^2+16+25+16化简得：BE^2-AE^2=9，即(BE+AE)(BE-AE)=9,又已知：BE-AE=1，解得:BE=5,AE=4,周长为29。

勾股定理知识领航一1．勾股定理：如果直角三角形的两直角边分别是a 、b ，斜边为c ，那么a 2＋b 2＝c 2．即直角三角形中两直角边的平方和等于斜边的平方．2．关于勾股定理的证明方法有很多．赵爽的证法是一种面积证法，其中的依据是图形经过割补拼接后，只要没有重叠，没有空隙，面积不会改变．“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智，它是我国古代数学的骄傲。

正因为此，这个图案被选为2002年在北京召开的世界数学家大会的会徽。

【例】 如图所示，可以利用两个全等的直角三角形拼出一个梯形．借助这个图形，你能用面积法来验证勾股定理吗？分析：面积法验证勾股定理关键是要找到一些特殊图形(如直角三角形，正方形，梯形)的面积之和等于另一些特殊图形的面积，从而达到验证的目的．解：此图可以这样理解，有三个Rt △其面积分别为21ab ，21ab 和21c 2．还有一个直角梯形，其面积为21(a ＋b )(a ＋b )． 由图形可知：21 (a ＋b )(a ＋b )＝ 21ab ＋21ab ＋21c 2 整理得(a ＋b )2＝2ab ＋c 2， a 2＋b 2＋2ab ＝2ab ＋c 2， ∴ a 2＋b 2＝c 2 .由此得到勾股定理．这正是美国第20任总统茄菲尔德证明勾股定理的方法．知识领航二1．在直角三角形中，若已知任意两边，就可以运用勾股定理求出第三边．无直角时，可作垂线构造直角三角形. 2.勾股定理的作用：（1）计算；（2）证明带有平方的问题；（3）实际应用．【例】甲、乙两位探险者到沙漠进行探险，没有了水，需要寻找水源．为了不致于走散，他们用两部对话机联系，已知对话机的有效距离为15千米．早晨8：00甲先出发，他以6千米/时的速度向东行走，1小时后乙出发，他以5千米/时的速度向北行进，上午10：00，甲、乙二人相距多远？还能保持联系吗？分析：要求甲、乙两人的距离，就要确定甲、乙两人在平面的位置关系，由于甲往东、乙往北，所以甲所走的路线与乙所走的路线互相垂直，然后求出甲、乙走的路程，利用勾股定理，即可求得甲、乙两人的距离．解：如图，甲从上午8：00到上午10：00一共走了2走了12千米，即OA=12． 乙从上午9：00到上午10：00一共走了1小时，走了5千米，即OB=5．在Rt △OAB 中，AB 2=122十52＝169，∴AB=13，因此，上午10：00时，甲、乙两人相距13千米． ∵15＞13， ∴甲、乙两人还能保持联系．答：上午10：00甲、乙两人相距13千米，两人还能保持联系．知识领航三1．利用勾股定理可以画出长度是无理数的线段，也就可以在数轴上画出表示无理数的点． 2．领会和掌握数形结合的数学思想方法.【例】右图是由36个边长为1的小正方形拼成的，连接小正方形中的点A 、B 、C 、D 、E 、F 得线段AB 、BC 、CD 、DE 、EF 、F A ，请说出这些线段中长度是有理数的是哪些？长度是无理数的是哪些？并在数轴上作出表示1、2、3、4、5的点. 解：如图，AB 2=AF 2+BF 2=22+12=5，BC 2=32+42=25，CD 2=12+32=10，DE =3，EF 2=ED 2+DF 2=32+42=25，F A =2.∴BC 、DE 、EF 、F A 的长是有理数，AB 、CD 的长度是无理数.在数轴上作出表示1、2、3、4、5的点如右图所示.练习提高一一、仔细读题，一定要选择最佳答案哟！ 1. 下列说法正确的是（ ）A.若 a 、b 、c 是△ABC 的三边，则a 2＋b 2＝c 2；B.若 a 、b 、c 是Rt △ABC 的三边，则a 2＋b 2＝c 2；C.若 a 、b 、c 是Rt △ABC 的三边， 90=∠A ，则a 2＋b 2＝c 2；D.若 a 、b 、c 是Rt △ABC 的三边， 90=∠C ，则a 2＋b 2＝c 2。

第一讲 勾股定理模块1、常见勾股数及辅助线例1．（1）如图，下列未知边的长度分别是 、 、 。

（2）如图，下列图形的面积分别是 、 、 。

解：（1）应用勾股定理：第1个直角三角形中两条直角边分别是3和4，所以斜边长为5；第2个直角三角形中斜边长为13，一条直角边长为5，所以另一条直角边的长为12； 第3个直角三角形中，斜边长为25，一条直角边长为24，所以另一条直角边的长为7。

（2）第1个直角三角形的斜边长为10，一条直角边长为8，另一条直角边长为6，所以三角形的面积是186242⨯⨯=； 第2个直角三角形的斜边长为1.3，一条直角边长为1.2，另一条直角边长为0.5， 所以三角形的面积是11.20.50.32⨯⨯=； 第3的图形中，小直角三角形的两条直角边分别为2和1.5，它的面积是S 1=1.5，斜边长为2.5，大直角三角形的斜边是6.5，一条直角边长为2.5，所以另一条直角边长为6， 面积S 2=12.567.52⨯⨯=， 于是面积等于S 1+S 2=9.例2．（1）如左图，梯形的周长为 ，面积为 ；如右图，梯形的周长为 ，面积为 ；?581.22222（2）下图的梯形ABCD 的对角线AC 和BD 相互垂直，已知AD =3，AC =9，BD =12，则BC 的长度为 。

解：（1）如图，平移得到直角三角形，斜边为20，一条直角边长为12，所以另一条直角边长为16，于是周长=20+10+16+22=68，面积=116(1022)2562⨯⨯+=； 第2个图中，做出两条高线，得到两个直角三角形，求得两条直角边长分别为0.5，0.9， 于是梯形的下底长为0.5+0.6+0.9=2，梯形的周长=0.6+2+1.3+1.5=5.4，面积=11.2(0.62) 1.562⨯⨯+=。

（2）如图平移AC 到DE ，连结CE ，CE =AD =3，DE =AC =9， 在直角三角形BDE 中，BD =12，DE =9，所以斜边BE =15， 解得BC =BE −CE =15−3=12。

六年级奥数几何问题之勾股定理与弦图
奥数，一直是长沙小升初的必考科目。

尤其是在“四大名校”的小升初选拔考试中，奥数往往就是拉开考生分数的一个重要题型。

因此，小升初的学生在备考阶段，千万不要忘了扎实的备考奥数知识。

下面，长沙奥数网网徐丽老师将会针对小升初奥数几何问题中的勾股定理与弦图问题，从知识点、常见解题方法、经典例题详解以及巩固练习四个方面来为来家进行讲解。

希望对大家有所帮助
一、知识点：
1、勾股定理
（1）、勾股定理
在我国，把直角三角形的两直角边的平方和等于斜边的平方这一特性叫做勾股定理或勾股弦定理，又称毕达哥拉斯定理或毕氏定理。

（2）、勾股定理的证明
二、常见解题方法：
1、勾股定理
勾股定理其实是一个很简单的定理，而我们小学奥数比较偏重于勾股定理的应用！首先，我们必须明确，勾股定理只能应用于直角三角形，这是大前提；其次就是，勾股定理描述的`是直角三角形的三边之间的数量关系！题目一旦牵涉到这些，我们都可以运用勾股定理来解决！
例1、若直角三角形一直角边为9，则斜边为多少？
【详解】此题是勾股定理和平方差公式的结合运用。

一直角边的长度为9，说明：斜边2-一直角边2=另一直角边2，即用字母表示为c2 -b2=a2=81=（c+b）（c-b），则
所以斜边长为41或15。

三、经典例题详解：
1、一个直角三角形，三条边的长度都是整数，其中一条边的长度是5，求三角形的面积？
【六年级奥数几何问题之勾股定理与弦图汇总】。

奥数勾股定理勾股定理，又称毕达哥拉斯定理，是一个关于直角三角形的重要定理。

它指出，在一个直角三角形中，斜边的平方等于两条直角边的平方和。

勾股定理的数学表达式为：a^2 + b^2 = c^2，其中a、b为直角边，c为斜边。

勾股定理在数学、物理等领域具有广泛的应用，它不仅是一个基本的几何定理，也是解决许多实际问题的关键工具。

在古代，我国的商高就已经提出了勾股定理的特例，而在西方，该定理由古希腊的毕达哥拉斯学派首次提出并证明。

勾股定理的证明方法有很多，其中比较著名的有几何证明、代数证明和切线证明等。

勾股定理的推广也有很多，例如在非欧几里得几何中，有双曲勾股定理和椭圆勾股定理等。

奥数中的勾股定理题型多种多样，主要可以分为以下几类：1. 直接应用勾股定理：这类题目直接给出一个直角三角形，要求利用勾股定理计算斜边或直角边的长度。

2. 勾股定理的逆定理：这类题目给出一个三角形，要求判断它是否为直角三角形，并说明理由。

勾股定理的逆定理指出，如果一个三角形的三条边满足a^2 + b^2 = c^2，那么这个三角形是直角三角形，且直角边为a、b，斜边为c。

3. 勾股定理与面积的关系：这类题目要求利用勾股定理计算直角三角形的面积。

根据勾股定理，直角三角形的面积可以表示为：√(a^2 + b^2) ×h，其中a、b为直角边，h为高。

4. 勾股定理与实际问题：这类题目将勾股定理应用到实际问题中，例如测量建筑物的高度、计算物体的体积等。

这类题目需要将实际问题抽象为数学问题，并利用勾股定理进行求解。

5. 勾股定理的推广与延伸：这类题目要求利用勾股定理解决更复杂的问题，例如在非欧几里得几何中讨论勾股定理、推广勾股定理到更高的维度等。

在奥数中，勾股定理的题目往往需要灵活运用勾股定理及其相关性质，通过合理设问、逐步深入，考查学生的思维能力和解决问题的能力。

前言：
该奥数系列讲座由多位一线国家特级教师针对当前最新的热点、考点、重点、难点、知识点，精心编辑而成。

（最新精品奥数系列讲座）
勾股定理
内容概述
1.勾股定理(毕达哥拉斯定理):直角三角形中的两直角边平方后的和等于斜边的平方．
公元前500年古希腊的毕达哥拉斯发现了勾股定理后,曾宰牛百头,广设盛筵以示庆贺．
2. 公元前11世纪的《周髀算经》中提到:故折矩,以为句广三,股修四、径修五．既方之.外半卿一矩,环而共盘.得成三、四、五．
三国时期的赵爽注解道:句股各自乘,并之为弦实,开方除之,即弦.案:弦图又可以句股相乘为朱实二,倍之为朱实四,以句股之差自相乘为中黄实,加差之,亦成弦实．
汉朝张苍、狄昌寿整理的《九章算术》第九卷为《句股》.其中
解释到:短面曰句，长面曰股，相与结角曰弦.句短其股，股短其弦．
句股各自乘，并，而开方除之，即弦． 中国科学院数学与系统科学研究院的徽标(右图所示)采用的就是赵爽
的弦图.2002年在北京举行的国际数学家大会的徽标也是弦图．
如下,在弦图中有EFGH S =
四边形()12ABCD MNPQ S S +矩形矩形C DG ADG CDE S S S '==
3. 伽菲尔德证法:美国第20任总统伽菲尔德对数学有浓厚的兴趣,在还是
中学教师时曾给出一种勾股定理的证明方法：
梯形面积=
12(上底＋下底)×高 =12
(a+b)×(a+b)。

第六讲 三角形、勾股定理一、 三勾股定理1. 勾股定理勾股定理：如果直角三角形的两直角边上分别为a,b ，斜边长为c ，那么222a b c +=。

即直角三角形两直角边的平方和等于斜边的平方.【例1】 （1）直角三角形中，两条直角边分别为6和8，求斜边的长.（2）直角三角形中，一条直角边为5，斜边为13，求另一条直角边.【例2】 直角三角形中，两条边长分别为3和4，求另一条边长。

【例3】 在直角三角形中，ABC ∆的A ∠为90°，顶点A 、B 、C 所对的边分别为a ，b ，c ，已知a=12，b=5，求c 。

2. 勾股定理的一些证明方法勾股定理发现迄今已有5000多年的历史，5000多年来世界上几个文明古国都相继发现和研究过这个定理。

几千年来，人们给出勾股定理很多证法，有人统计，现在世界上已找到400多种证明方法，但十七种方法比较巧妙的，有以下几种。

（1） 中国著名数学家赵爽的正方形面积证明方法。

我国古代著名数学家赵爽在《勾股圆方图》一书中的证明，是比较简洁优美的方法。

如图18-4，在边长为c 的正方形中，有四个斜边为c 的全等的直角三角形，已知他们的直角边为a 、b ，利用这个图，证明勾股定理。

解答 因为正方形边长为c 所以正方形面极为2c 。

又因为正方形面积=4×12ab +()222a b a b -=+所以222a b c += （2） 古希腊数学家毕达哥拉斯的旋转证法。

公元前约500年古希腊有位著名的哲学家、数学家毕达哥拉斯在生活中的一个偶然事件中，发现了勾股定理和它的证明方法。

如图18-5，设矩形ABCD 为火柴盒侧面，将这个火柴盒推倒至A′B′C′D 的位置，D 点不动.若设AB=a ，BC=b ，DB=c ，则梯形A′B′BC 面积()()()21122S a b a b a b =++=+梯形ABBC ，又"""2111222BCD A B D DBB S S S S ab c ab ∆∆∆=++=++""梯形A B BC 所以()2211112222a b ab c ab +=++则22222a b ab c ab ++=+即222a b c +=（3） 美国第20任总统伽菲尔德的割、移、补、拼证法。