与内切球外接球半径相关的问题
- 格式:doc
- 大小:277.19 KB
- 文档页数:8


内切球和外接球常见解法内切球和外接球是在几何学中常用的概念,它们分别指的是一个几何体内切或外接于另一个几何体的球。
在实际问题中,内切球和外接球常常用于优化问题和几何问题的求解,其解法也有多种。
以下将介绍一些常见的解法。
1. 解法一:利用勾股定理求解。
内切球和外接球都可以利用勾股定理求解。
以内切球为例,我们可以考虑任意三角形ABC,设其内切球的半径为r,以I为内切圆心,则:AB + AC = 2r;AC + BC = 2r;AB + BC = 2r。
整理可得:r = [ABC] / (s + a + b + c),其中s为半周长,a、b、c为三角形ABC的三边长,[ABC]为三角形ABC的面积。
而外接球的半径r'则可用公式r'=[ABC] / (4S),其中S为三角形ABC的外接圆半径。
欧拉定理是内切球和外接球求解的另一个重要工具。
欧拉定理有两种形式,分别为:对于任意四面体,其四个顶点、三条棱的中点和六面体质心共九个点在同一球面上。
对于任意三角形ABC,其外接圆心、垂足交点、垂心、重心四点在同一圆上,且圆心为外接球心。
利用欧拉定理可以求得内切球半径:点O为六面体质心,点I为内切圆心,则IO等于内切球半径r。
点O为三角形外心,点H为垂心,点G为重心,则OG等于外接球半径r'。
对于一些优化问题,内切球和外接球也可以通过线性规划求解。
例如,对于一个凸多面体,求其内切球或外接球的半径最大值,可以将问题转化为线性规划问题,即:max rs.t. A_i * x <= b_i, i=1,2,...,mx_i >= 0, i=1,2,...,n其中,A_i是多面体的几何信息,b_i是多面体中某一点到各个面的距离,x是优化变量,r就是所需要求的内切球或外接球半径。
可以使用线性规划求解器求解其最优解。

立体几何外接球和内切球十大题型
立体几何中的外接球和内切球是常见的题型,下面我将列举十个常见的题型并进行解答。
1. 求立方体的外接球和内切球的半径。
外接球的半径等于立方体的对角线的一半,内切球的半径等于立方体的边长的一半。
2. 求正方体的外接球和内切球的半径。
外接球的半径等于正方体的对角线的一半,内切球的半径等于正方体的边长的一半。
3. 求圆柱体的外接球和内切球的半径。
外接球的半径等于圆柱体的底面半径,内切球的半径等于圆柱体的高的一半。
4. 求圆锥的外接球和内切球的半径。
外接球的半径等于圆锥的底面半径,内切球的半径等于圆锥的高的一半。
5. 求球的外接球和内切球的半径。
外接球的半径等于球的半径的根号3倍,内切球的半径等于球的半径的一半。
6. 求棱锥的外接球和内切球的半径。
外接球的半径等于棱锥的底面边长的一半,内切球的半径等于棱锥的高的一半。
7. 求棱柱的外接球和内切球的半径。
外接球的半径等于棱柱的底面边长的一半,内切球的半径等于棱柱的高的一半。
8. 求四面体的外接球和内切球的半径。
外接球的半径等于四面体的外接圆的半径,内切球的半径等
于四面体的内切圆的半径。
9. 求正六面体的外接球和内切球的半径。
外接球的半径等于正六面体的对角线的一半,内切球的半径等于正六面体的边长的一半。
10. 求正八面体的外接球和内切球的半径。
外接球的半径等于正八面体的对角线的一半,内切球的半径等于正八面体的边长的一半。
以上是关于立体几何中外接球和内切球的十个常见题型及其解答。
希望能对你有所帮助。

正方体的外接球与内切球问题简介
本文讨论正方体的外接球与内切球问题。
外接球问题
正方体的外接球是指一个球,它能够刚好与正方体的每个顶点接触,并且球心在正方体外部。
解决正方体的外接球问题可以采用以下步骤:
1. 首先找到正方体的对角线长度,记为d。
2. 外接球的直径等于正方体的对角线长度,即2d。
3. 外接球的半径等于直径的一半,即d。
因此,正方体的外接球的半径等于对角线长度的一半。
内切球问题
正方体的内切球是指一个球,它能够刚好与正方体的每个面接触,并且球心在正方体内部。
解决正方体的内切球问题可以采用以下步骤:
1. 首先找到正方体的边长,记为a。
2. 内切球的直径等于正方体的边长,即a。
3. 内切球的半径等于直径的一半,即a/2。
因此,正方体的内切球的半径等于边长的一半。
总结
通过上述讨论,我们得出了正方体的外接球和内切球的半径计算方法。
这些结果可以在几何学和物理学中得到应用。
希望本文能够帮助您理解正方体的外接球与内切球问题。
---
以上为回答内容, 仅供参考。

空间圆柱体的外接球和内切球问题简介在三维几何中,圆柱体(cylinder)是一个具有圆底和圆顶的几何体。
本文讨论了圆柱体的外接球和内切球问题。
外接球圆柱体的外接球是一个能够完全包围圆柱体的球体。
具体来说,外接球的球心与圆柱体的底面圆心以及顶面圆心都在同一直线上,并且外接球的半径等于这个直线与圆柱体底面、顶面中任意一个圆的半径之和。
对于一个给定的圆柱体,外接球的半径可以通过以下公式计算:$$R = \sqrt{h^2 + r^2}$$其中,$R$ 是外接球的半径,$h$ 是圆柱体的高度,$r$ 是圆柱体底面圆的半径。
内切球圆柱体的内切球是一个与圆柱体的底面和顶面相切的球体。
具体来说,内切球的球心与圆柱体的底面圆心以及顶面圆心都在同一直线上,并且内切球的半径等于这个直线与圆柱体底面、顶面中任意一个圆的半径之差。
对于一个给定的圆柱体,内切球的半径可以通过以下公式计算:$$r_{\text{in}} = \sqrt{h^2 + (R - r)^2}$$其中,$r_{\text{in}}$ 是内切球的半径,$h$ 是圆柱体的高度,$R$ 是外接球的半径,$r$ 是圆柱体底面圆的半径。
结论本文讨论了圆柱体的外接球和内切球问题。
外接球是一个能够完全包围圆柱体的球体,其半径可以通过一个简单的公式计算得到。
内切球是一个与圆柱体的底面和顶面相切的球体,其半径也可以通过一个公式计算得到。
这些问题在几何学和工程学中具有重要的应用价值。
> 注意:以上内容为解答圆柱体的外接球和内切球问题的基本原理和公式,具体计算应考虑实际情况和应用环境。
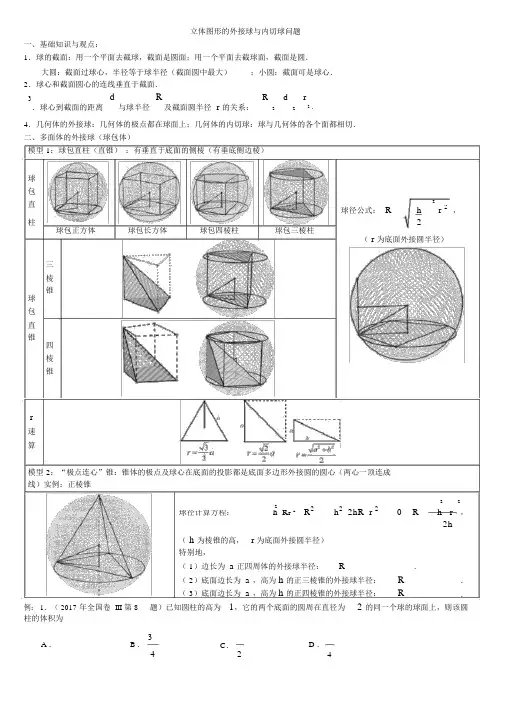
立体图形的外接球与内切球问题一、基础知识与观点:1.球的截面:用一个平面去截球,截面是圆面;用一个平面去截球面,截面是圆.大圆:截面过球心,半径等于球半径(截面圆中最大);小圆:截面可是球心.2.球心和截面圆心的连线垂直于截面.3 d与球半径R及截面圆半径 r 的关系:R2d2r2 ..球心到截面的距离4.几何体的外接球:几何体的极点都在球面上;几何体的内切球:球与几何体的各个面都相切.二、多面体的外接球(球包体)模型 1:球包直柱(直锥):有垂直于底面的侧棱(有垂底侧边棱)球包直h 2球径公式: R r 2,柱 2球包正方体球包长方体球包四棱柱球包三棱柱( r 为底面外接圆半径)三棱锥球包直锥四棱锥r速算模型 2:“极点连心”锥:锥体的极点及球心在底面的投影都是底面多边形外接圆的圆心(两心一顶连成线)实例:正棱锥22 2 R2 h2 2hR r 2 0 R h r球径计算方程:h R r 2 ,2h( h 为棱锥的高,r 为底面外接圆半径)特别地,( 1)边长为a正四周体的外接球半径:R ______________.( 2)底面边长为a,高为h的正三棱锥的外接球半径:R __________.( 3)底面边长为a,高为h的正四棱锥的外接球半径:R __________.例: 1.( 2017 年全国卷 III 第 8 题)已知圆柱的高为 1,它的两个底面的圆周在直径为 2 的同一个球的球面上,则该圆柱的体积为A .B .3D .C.42 42【分析】 模式辨别:“球包体” 中的 “垂底侧边棱 (母线)”种类, h1 , R 1,底面半径为 r ,则由 Rhr 2223,V得: 121 r 2r 2r 2h3 .2442.( 2010 年全国新课标卷第 10 题)设三棱柱的侧棱垂直于底面,全部棱的长都为 a ,极点都在一个球面上,则该球的表面积为A . a 2B .7a 2C .11a 2D . 5 a 2333a , R2h2a 2a 2 7a 2【分析】“球包体”中的“垂底侧边棱”种类,h a , rr 2 ,3243 12因此该球的表面积 S 4 R247a 2 7a 2 .答案 B .12 33.( 2014 年全国纲领卷第 8 题)正四棱锥的极点都在同一球面上,若该棱锥的高为4,底面边长为 2,则该球的表面积为81B . 16C . 9D .27A .44【分析】模式辨别: “球包体”中的“极点连心锥” , h 4 , r2 22 ,则 Rh 2 r 2 162 922h8,4因此 S 4R 2 481 81,答案: A .16 48 cm ,将一个4.( 2013 年全国卷 I 第 6 题)如图,有一个水平搁置的透明无盖的正方体容器,容器高球放在容器口,再向容器内灌水,当球面恰巧接触水面时测得水深为6 cm ,假如不计容器的厚度,则球的体积为A . 500 cm 3B . 866 cm 3C . 1372 cm 3D . 2048 cm 33333【分析】设水面与球的接触点(切点)为P ,球心为 O ,则 PO 垂直于正方体的上表面,依题意Ph 2r4R2r 2R 2 ,到正方体上表面的距离为,球与正方体上表面订交圆的半径,有: 2r 245 ,因此球的体积 V43500R3 R.43三、安心大法:球心在过截面圆的圆心且垂直于截面圆所在平面的直线上.两圆安心法:以下列图,过两个截面圆的圆心分别作相应截面圆的垂线,由两垂线的交点确立圆心.例 2:1.已知边长为 2 3 的棱形ABCD 中,60,现沿对角线BD折起,使得二面角A BDC 为 120,此时点 A , B , C , D 在同一个球面上,则该球的表面积为(A . 20B . 24C . 28)D . 322.在矩形ABCD 中,AB 4 ,BC 3,沿AC 将矩形折成一个直二面角 B AC D ,则四周体ABCD 的外接球的体积为___________.3.在边长为1的菱形ABCD 中,BAD 60 ,沿对角线将菱形折成直二面角A BD C ,则三棱锥 A BCD 的外接球的表面积为_____________.四、正多面体的内切球(体中球)锥体的内切球:圆锥的内切球:边长为 a 的正方体:等边圆柱(母线 a ):边长 a 的正八面体:R ____________.R a a.RR R2 2五、正多面体的“切边球”(与全部的棱都相切的球)正四周体边长为 a ,球半径R 正方体边长为 a ,球半径R 正四周体边长为 a ,球半径R例 3:1.一个球的外切正方体的全面积为 6 ,则球的体积为_________.2.某圆锥的截面为边长为 2 的正三角形,则该圆锥的内切球的表面积为_______.3.( 2016 年全国卷 III 第 10 题)在关闭的直三棱柱ABC A1B1C1内有一个体积为V的球,若AB BC , AB 6 ,BC 8,AA13,则 V 的最大值是A .49C.632B .D.3 2【分析】考察直三棱柱中截面的内切圆为球的大圆的情形,有 6 8 10 R 6 8 R 2 AA1 3,故当球半径为3时球的体积最大为 V 4 R3 4 272 2.答案 B .2 3 3 8 2练习:1.( 2015 年全国卷 II 第 9 题)已知A,B是球O的球面上两点,AOB 90 , C 为该球面上的动点,若三棱锥O ABC 体积的最大值为36,则球 O 的表面积为A .36B .64 C.144 D .2562.( 2016 年福建漳州市 5 月质检)三棱锥S ABC 中, SB 平面 ABC ,SB 5 ,ABC 是边长为 3 的正三角形,则三棱锥 S ABC 的外接球的表面积为()A .3B .5 C.9 D .123.( 2014 年湖南卷)一块石材表示的几何体的三视图以下图,将该石材切削、打磨,加工成球,则能获得的最大球的半径等于()A .1B .2 C.3 D .44(. 2013 年辽宁卷理 10)已知三棱柱ABC A1B1C1的6个极点都在球O的球面上,若AB 3,AC 4 , AB AC , AA 1 12 ,则球 O 的半径为()A . 3 17B . 2 10C .13D . 3 10225.( 2012 年全国新课标卷第 11 题)已知三棱锥 S ABC 的全部极点都在球 O 的球面上, ABC 是边长为 1 的正三角形, SC 为球 O 的直径,且 SC2 ,则此棱锥的体积为A .2B .3C .223D .6626.在正三棱锥 P ABC 中, PA PB PC3 ,侧棱 PA 与底面 ABC 所成的角为 60 ,则该三棱锥外接球的体积为()A .B .C . 44D .337.已知底面边长为 1,侧棱长为2 的正四棱柱的各极点均在同一个球面上,则该球的体积为()A .32B . 4C . 2D .4338.( 2017 年福建省质检) .空间四边形 ABCD 的四个极点都在同一球面上, E 、 F 分别是 AB 、 CD 的中点,且EF AB, EF CD ,若 AB 8,CD EF 4 ,则该球的半径等于A . 65 2B . 65 2C .65D . 6516829.若三棱锥 PABC 的最长的棱 PA 2 ,且各面均为直角三角形,则此三棱锥的外接球的体积是 __________.10 .( 2008 年 高 考 浙江 卷 理 14) 已 知 球 O 的 面 上 四 点 A 、 B 、 C 、 D , DA平 面 ABC , AB BC , DAAB BC3 ,则球 O 的体积为 ____________ .11.( 2016 年东北三省三校联考)三棱柱ABC A 1B 1C 1 各极点都在一个球面上,侧棱与底面垂直,ACB 120 ,CA CB 2 3 , AA 1 4 ,则这个球的表面积为 ____________ .12.在三棱柱 ABC A 1B 1C 1 中,侧棱 AA 1 垂直底面, ACB 90 , BAC 30 , BC 1,且三棱柱 ABC A 1B 1C 1的体积为 3 ,则三棱柱 ABCA 1B 1C 1 的外接球表面积为 _________.13.在正三棱锥 S ABC 中, M , N 分别是棱 SC 、 BC 的中点,且 AMMN ,若侧棱 SA 2 3 ,则正三棱锥S ABC 外接球的表面积是 ____________.14.在三棱锥A BCD 中, AB CD 2 , AD BC 5 , AC BD 7 ,则三棱锥 A BCD 外接球的表面积为 __________.15.( 2017 年天津卷)已知一个正方体的全部极点在一个球面上,若这个正方体的表面积为18 ,则这个球的体积为 ______.16.( 2017 年江苏卷)如图,在圆柱 O 1O 2 内有一个球,该球与圆柱的上、下底面及母线均相切,记圆柱 O 1O 2 的体积为 V 1 ,球 O 的体积为 V 2 ,则V 1的值是 _____________.V 2。

高考数学中的内切球和外接球问题一、有关外接球的问题如果一个多面体的各个顶点都在同一个球面上,那么称这个多面体是球的内接多面体,这个球称为多面体的外接球.有关多面体外接球的问题,是立体几何的一个重点,也是高考考查的一个热点.考查学生的空间想象能力以及化归能力.研究多面体的外接球问题,既要运用多面体的知识,又要运用球的知识,并且还要特别注意多面体的有关几何元素与球的半径之间的关系,而多面体外接球半径的求法在解题中往往会起到至关重要的作用.一、直接法(公式法)1、求正方体的外接球的有关问题例1若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为______________ .27π.例2 一个正方体的各顶点均在同一球的球面上,若该正方体的表面积为24,则该球的体积为______________.43π.2、求长方体的外接球的有关问题例3一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱长分别为1,2,3,则此球的表面积为.14π.例4、已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积为(). CA. 16πB. 20πC. 24πD. 32π3.求多面体的外接球的有关问题例5. 一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为89,底面周长为3,则这个球的体积为 .解 设正六棱柱的底面边长为x ,高为h ,则有263,1,2936,384x x x h h =⎧⎧=⎪⎪∴⎨⎨=⨯⎪⎪=⎩⎩.∴正六棱柱的底面圆的半径21=r ,球心到底面的距离23=d .∴外接球的半径22d r R +=. 体积:334R V π=. 小结 本题是运用公式222R r d =+求球的半径的,该公式是求球的半径的常用公式.二、构造法(补形法) 1、构造正方体例5 若三棱锥的三条侧棱两两垂直,且侧棱长均为3,则其外接球的表面积是_______________.9π.例3 若三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积是 .故其外接球的表面积249S R ππ==.小结:一般地,若一个三棱锥的三条侧棱两两垂直,且其长度分别为a b c 、、,则就可以将这个三棱锥补成一个长方体,于是长方体的体对角线的长就是该三棱锥的外接球的直径.设其外接球的半径为R ,则有2222R a b c =++.出现“墙角”结构利用补形知识,联系长方体。

圆柱体的外接球与内切球问题概述:在三维空间中,我们可以构造各种各样的几何体,其中许多几何体都可以与球体相互联系。
本文将讨论圆柱体,特别是将重点放在圆柱体的外接球和内切球上。
这两个球对于圆柱体的研究有很大的启示作用,同时也引发了一些有趣的数学问题和实际应用。
正文:圆柱体是一种常见的几何体,其形状简单,易于描述和理解。
一个圆柱体可以由一个圆在平面上绕着一条与圆在同一平面内的直线运动而成。
我们很容易能够想象出一个圆柱体,并且知道它有一个底面和一个顶面,以及侧面连接这两个面。
但是,圆柱体围绕着一个特殊的轴运动时,就会出现外接球和内切球。
这些球形几何体有很多有趣的性质和应用,因此吸引了众多数学爱好者的关注。
首先,我们要明确外接球和内切球的概念。
一个几何体的外接球是指一个球体,其球面恰好可以切到几何体的每个顶点上。
类似地,内切球是指一个球体,其球面正好与几何体相切,并且几何体的每个面都是球面的切面。
对于一个圆柱体而言,其外接球和内切球具有以下性质:1. 圆柱体外接球的半径等于圆柱体的直径。
这个性质很容易证明,因为当圆柱体沿着其轴翻滚时,其每个顶点都位于相同的圆周上,因此外接球的球心也会位于这个圆周上。
2. 圆柱体内切球的半径等于圆柱体侧面的高。
对于圆柱体而言,内切球的球心位于圆柱体的轴线上,因此球心到底面和顶面的距离就等于圆柱体的侧面高度。
除了这些基本性质外,圆柱体的外接球和内切球还有很多有趣的实际应用。
例如,在工程设计中,需要确定一个物体的最小包围球来判断其尺寸是否符合要求;在计算机图形学中,可以使用外接球和内切球来判断一个物体是否在另一个物体之内或之外。
此外,外接球和内切球也是许多数学问题的研究对象,如最小球覆盖问题、球装配问题等等。
总结:圆柱体的外接球和内切球问题虽然看起来很简单,但是背后有许多有趣的数学性质和实际应用。
了解这些性质可以帮助我们更好地理解圆柱体和球形几何体之间的关系,并且有助于我们解决实际问题。

高中数学解题指导八个无敌模型全搞定空间几何的外接球和内切球问题八个有趣模型——搞定空间几何体的外接球与内切球类型一、墙角模型墙角模型是指三条线段两两垂直的几何体,通过公式(2R) = a + b + c,即2R = a^2 + b^2 + c^2,可以求出其外接球半径R。
例1:1)已知顶点都在同一球面上的正四棱柱的高为4,体积为16,求该球的表面积。
解:由V = ah = 16,得a = 2,4R = a + a + h = 4 + 4 + 16 = 24,S = 24π,答案为C。
2)若三棱锥的三个侧面两两垂直,且侧棱长均为3,求其外接球的表面积。
解:由2R = a + b + c = 3 + 3 + 3 = 9,得R = 9/4,S =4πR^2 = 9π。
3)在正三棱锥S-ABC中,M、N分别是棱SC、BC的中点,且AM⊥MN,若侧棱SA = 23,求正三棱锥S-ABC外接球的表面积。
解:由墙角模型的特点可知,正三棱锥的对棱互垂直。
连接AB、BC的中点D、E,连接AE、CD,交于H,则H是底面正三角形ABC的中心。
由AM⊥MN,SB//MN,可得AM⊥SB,AC⊥SB,故SB⊥平面SAC,SB⊥SA,SB⊥SC,即SB⊥SA,BC⊥SA,故SA⊥平面SBC,SA⊥SC。
因此,三棱锥S-ABC的三棱条侧棱两两互相垂直,由2R^2 = 23^2 + 23^2 + 23^2 = 36,得R^2 = 9,S = 36π。
类型二、棱台模型棱台模型是指上底面和下底面都是正多边形,且两底面中心连线与侧棱垂直的几何体。
通过勾股定理和相似三角形,可以求出其外接球半径R和内切球半径r。
例2:1)已知棱台的上底面和下底面都是正三角形,上底边长为3,下底边长为6,侧棱长为5,求其外接球半径R和内切球半径r。
解:由勾股定理可得棱台的高为4√3.设外接球半径为R,内切球半径为r,则有R/r = (a + b + c)/(a + b - c) = (3 + 6 +5)/(3 + 6 - 5) = 7,解得R = 7r。


与内切球外接球半径相关的问题有关于内切球、外接球的问题,应该说是一个比较困难的问题,几乎所有同学都会感到无从下手,这是正常的,因为这类问题需要强有力的想象力,同时方法性极强。
我们就这部分问题,尽量总结全面。
1. 内切球和外接球的基本定义;立体图形的内切球是指:与该立体图形的所有面都相切的球,注意是与所有面都相切,因此,很多立体图形是不存在内切球的。
基本性质是:球心到所有面的距离相等,且为内切球半径。
立体图形的外接球是指:立体图形的所有顶点都在球面上。
基本性质是:球心到所有顶点的距离相等,且为外接球半径。
2.长方体的外接球:长方体中从一个顶点出发的三条棱长分别为c b a ,,,则体对角线长为222c b a l ++=,几何体的外接球直径R 2,长方体体对角线长l ,则2222c b a R ++=3.正方体的外接球:正方体的棱长为a ,则正方体的体对角线为a 3,其外接球的直径R 2为a 3。
4.正四面体的内切球、外接球(1)正四面体的内切球球心和外接球球心是重合的,并且都在正四面体的高线上。
(2)正四面体的高若为h ,则外接球半径34R h =,内切球半径14r h = 5. 直棱柱的外接球:直棱柱外接球半径的思想是:找出直棱柱的外接圆柱,圆柱的外接球就是所求直棱柱的外接球。
(1) 直棱柱的体对角线长就是外接球的直径,这是核心。
(2) 直棱柱的体对角线2=底面图形的外接圆直径2+侧棱(即高)26.正棱锥的外接球:正棱锥外接球半径的思想是:球心在正棱锥的高线上,根据球心到各个顶点的距离是外接球半径,列出关于半径的方程。
我们需要考虑将“球心”“底面正多边形的中心”“底面上任一个顶点”这三个点连接起来,构成一个直角三角形,利用勾股定理,列出关于半径的方程。
一般来说这个方程是:222()h R a R -+=或222()R h a R -+=,这里的h 是指正棱锥的高,a 是指底面正多边形的对角线长的一半,若底面为正三角形时,a 是指正三角形中线长的23,考生可以划出一个图形,印证一下这些内容。
空间正方体的外接球和内切球问题外接球
外接球是一个与正方体相切于所有顶点的球体。
换句话说,外接球的球心与正方体的顶点相重合,并且球体的半径刚好与正方体的边长相等。
由于正方体的六个顶点之间的距离是相等的,所以外接球也是一个等边球体。
外接球的性质有以下几点:
1. 外接球的球心与正方体的中心重合。
2. 外接球的半径等于正方体的边长。
内切球
内切球是一个与正方体的六个面相切的球体。
换句话说,内切球的球心位于正方体的中心,并且球体的半径刚好与正方体的边长的一半相等。
内切球的性质有以下几点:
1. 内切球的球心与正方体的中心重合。
2. 内切球的半径等于正方体的边长的一半。
外接球和内切球的关系如下:
1. 外接球的半径等于内切球半径的两倍。
2. 外接球的球心和内切球的球心重合。
外接球和内切球的问题在几何学和工程学中具有一定的应用价值。
通过研究它们的性质和特点,可以帮助我们更好地理解立体几何和球体的关系。
本文只是简单介绍了空间正方体的外接球和内切球问题,希望能对您有所帮助。
如需深入了解此问题,还需进一步研究和探索。
第二章:外接球与内切球1.空间几何体的内切球几何体示例图像截面图对应性质圆柱r h 、分别为圆柱的底面圆半径和高,R 为内切球半径.R r =且2h R =;正三棱柱r h 、分别为柱体的底面三角形内切圆半径和高,R 为内切球半径.R r =且2h R =;正棱锥PE 为锥体的斜高,h r 、分别为锥体的高和底面内切圆半径,R 为内切球半径.1POF PEO △∽△可得R OP h R r PE PE -==“钻石”PE 为锥体的斜高,h r 、分别为锥体的高和底面内切圆半径,R 为内切球半径.在Rt POE △中,满足h rR PE⋅=一般三棱锥记R 为内切球半径,三棱锥的四个面面积分别为1234S S S S 、、、,则1234VR S S S S =+++【示例1】1.如图,在圆柱12O O 内有一个球O ,该球与圆柱的上、下底面及母线均相切,记圆柱12O O 的体积为1V ,球O 的体积为2V ,则12V V =__________.【解析】记内切球半径为R ,底面圆半径为r ,圆柱高为h ;则R r =且2h R =;则23122V h s r r r ππ=⋅=⋅=,3324433V R r ππ==;∴1232V V =2.如果一个球的外切圆锥的高是这个球的半径的3倍,则圆锥的侧面面积和球的表面积之比为__________.【解析】轴截面如右图,记h r 、为圆锥的高和底面圆半径,R 为内切球半径;由题意,3h R =,同时由1POF PEO △∽△可得1OP OFPE EO =;即R r==,得r =,则PE =.∴在圆锥1O P 中,2212S PE r R ππ=⋅=侧,2=4S R π球;则:3:1S S =侧球【例1】1.已知正方体的内切球(球与正方体的六个面都相切)的体积是323π,则该正方体的表面积为__________.2.如果一个八面体各个面都是全等的正三角形,如图所示,则这个几何体叫正八面体,则棱长为4的正八面体的内切球半径是__________.3.在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球,若AB BC ⊥,6AB =,8BC =,13AA =,则V 的最大值是__________.4.天津滨海文化中心地处天津滨海新区开发区,是天津乃至京津冀地区的标志性文化工程.其中滨海图书馆建筑独具特色,被称为“滨海之眼”,如图1所示,中心球状建筑引起了小明的注意,为了测量球的半径,小明设计了两个方案,方案甲,构造正三棱柱侧面均与球相切如图2所示,底面边长约为30米,估计此时球的完整表面积为平方米;方案乙,测量球被地面截得的圆的周长约为16π米,地面到球顶部高度约为16米,估计此时球的完整体积为立方米,你认为哪种方案好呢?课堂练习1:1.一个球与一个正三棱柱的三个侧面和两个底面都相切,已知这个球的体积是32,那么3这个球的半径是,三棱柱的体积是.2.正四棱锥的高与底面边长相等且体积为83,(1)以底面中心为球心,经过四棱锥四条侧棱中点的球的表面积为__________;(2)该正四棱锥的内切球体积为__________.3.农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,俗称“粽子”,古称“角黍”,是端午节大家都会品尝的食品,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.如图,平行四边形形状的纸片是由六个边长为1的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为;若该六面体内有一球,则该球体积的最大值为.2.柱体外接球问题概述具备外接球的柱体,一定是“直”的,即侧棱垂直于底面或圆柱体.其球心必在柱体上下底面外接圆圆心连线的中点.此时球心到柱体底面的距离d 等于柱体高h 的一半(即2h d =).示例图像圆柱长方体直三棱柱计算公式222224h R d r r =+=+22224R a b c =++2sin ar A=,222R d r =+问题设计①.先求出柱体高和底面相关信息,再求外接球半径;②.已知外接球半径,求柱体的高或底面相关变量.【示例2】1.如图,长方体1111ABCD A B C D -的底面是面积为2的正方形,该长方体的外接球体积为323π,点E 为棱AB 的中点,则三棱锥1D ACE -的体积是__________.【解析】Ⅰ.确定长方体的高→Ⅱ.求1D ACEV -3432233V R R ππ==→=球,则2222114222AB AD AA R AA AB AD ⎫++=⎪→=⎬==⎪⎭;∴在三棱锥1D ACE -中,122112ACE h AA S AE BC ⎧==⎪⎨=⋅=⎪⎩△;得112233D ACE ACE V h S -=⋅=△2.已知直三棱柱111ABC A B C -的外接球半径为4,同时BA BC ⊥,BA BC =则111ABC A B C -体积的最大值为__________.【解析】Ⅰ.找到侧棱和底面棱长的关系→Ⅱ.函数求最值显然Rt ABC △为等腰直角三角形,则22r AB =;此时212ABC S AB CB r =⋅=△;同时222224h R d r r =+=+可得22164h r =-;则()()23116640844ABCh V h S h h h h ⎛⎫=⋅=⋅-=-<< ⎪⎝⎭△;令()()36408f x x x x =-+<<,则()2364f x x '=-+;令()0f x '=得x =;∴()f x 在⎛ ⎝上递增,在⎫⎪⎭上递减,则()max 9f x f ==,则()max max14V f x ==【例2】1.若一个圆柱的轴截面是面积为4的正方形,则该圆柱的外接球的表面积为__________.2.在正方体1111ABCD A B C D -中,三棱锥11A B CD -的表面积为,则正方体外接球的体积为__________.3.已知直三棱柱的各棱长都相等,三棱柱的所有顶点都在球O 的表面上,若球O 的表面积为28π,则该三棱柱的体积为__________.4.如图,直三棱柱111ABC A B C -的六个顶点都在半径为1的半球面上,AB AC =,侧面11BCC B 是半球底面圆的内接正方形,则侧面11ABB A 的面积为__________.5.“迪拜世博会”于2021年10月1日至2022年3月31日在迪拜举行,中国馆建筑名为“华夏之光”,外观取型中国传统灯笼,寓意希望和光明.它的形状可视为内外两个同轴圆柱,某爱好者制作了一个中国馆的实心模型,已知模型内层底面直径为12cm ,外层底面直径为16cm ,且内外层圆柱的底面圆周都在一个直径为20cm 的球面上.此模型的体积为__________.课堂练习2:1.已知正方体的体积是8,则这个正方体的外接球的体积是__________.2.在正方体1111ABCD A B C D -中,三棱锥11A B CD -的表面积为,则正方体外接球的体积为__________.3.一直三棱柱的每条棱长都是2,且每个顶点都在球O 的表面上,则球O 的表面积为__________.4.已知一个体积为8的正方体内接于半球体,即正方体的上底面的四个顶点在球面上,下底面的四个顶点在半球体的底面圆内.则该半球体的体积为__________.3.侧棱垂直于底面的锥体外接球问题阐述若锥体有一条侧棱PA 满足PA ⊥底面ABC ,则该锥体必可还原成一个直棱柱.即侧棱垂直于底面的棱锥与还原之后的直棱柱具有相同的外接球.示例图像还原至长方体还原至长方体还原至直三棱柱对应条件AP AB AC 、、两两垂直AP AB BC 、、两两垂直PA ⊥面ABC 计算公式22224R AP AB AC =++22224R PA AB BC =++12sin AB r C =⋅且12d h =222R d r =+备注当锥体有三条棱两两垂直时,记这三条棱的棱长分别为a b c 、、,则22224R a b c =++.若锥体的底面不含直角,仅有侧棱垂直于底面时,用222R d r =+求出外接球半径【示例3】在三棱锥P ABC -中,90ACB ∠=︒,8AB =,PC ⊥面ABC 且6PC =,则该三棱锥外接球的表面积为__________.【解析】由题意可知CA CB CP 、、两两垂直;则222222222464410041006R CP CB CA CA CB AB R S R CP ππ⎫=++⎪+==→=→==⎬⎪=⎭【例3】1.在三棱锥A BCD -中,AB AC AD 、、两两垂直,且ACB ACD ABD △、△、△的面积分别为22A BCD -的外接球的表面积为__________.2.在三棱锥P ABC -中,PA ⊥平面ABC ,且ABC △为等边三角形,2AP AB ==,则三棱锥P ABC -的外接球的表面积__________.3.如图,PA ⊥面ABCE ,其中ABCD 为正方形,2AD =,1ED =.若三棱锥P ADE -的外接球的体积为92π.则四棱锥P ABCD -的外接球的表面积为__________.课堂练习3:1.在边长为2的等边三角形ABC 中,点D 是BC 的中点.以AD 为折痕,将ABC △折成直二面角B AD C --,则过A B C D 、、、四点的球的表面积为__________.2.在四面体S ABC -中,SA ⊥平面ABC ,120BAC ∠=︒,1AB =,2AC =,3SA =,则该四面体外接球面积为__________.3.在《九章算术》中,将底面为矩形且有一条侧棱与底面垂直的四棱锥称为阳马.已知四棱锥M ABCD -为阳马,侧棱MA ⊥底面ABCD ,且1MA =,2BC =,3AB =.若该四棱锥的顶在都在同一球面上,则该球的表面积为__________.4.正棱锥和圆锥的外接球补充:问题阐述①.正四面体内嵌于正方体,则两者具有相同的外接球.记正四面体的边长为a ,正方体的边长为b ,外接球半径为R ;②.两个具有相同底面,且顶点(P Q 、)在底面的射影均为底面外接圆圆心的锥体的外接球.记底面外接圆半径为r ,两个锥体的高分别为12h h 、,外接球半径为R示例图像对应计算①.2a b =且2243R b =;②.22342R a =①.122h h R +=且PA QA ⊥(PQ 为球的直径);②.212r h h =⋅(直角三角形内射影定理);【示例4】1.正三棱锥底面边长为3,侧棱与底面成60︒角,则其外接球的体积为__________.【解析】Ⅰ.确定正棱锥的高和底面外接圆半径ABC △是边长为3的等边三角形,则333r AB ==;在Rt POA △中,3360OA r OP h PAO ⎫==⎪→==⎬∠=︒⎪⎭;Ⅱ.求外接圆半径,并求其体积则2231243222633h r R V R h ππ+===→==2.两个圆锥的底面是一个球的同一截面,顶点均在球面上,若球的体积为323π,两个圆锥的高之比为1:3,则这两个圆锥的体积之和为__________.【解析】Ⅰ.求出12R h h r→→、3432233V R R ππ==→=球,显然PQ 是球O 的直径,则PA QA ⊥,则212r h h =⋅;121122243331h h R h r h h h +===⎫⎧→→=⎬⎨==⎭⎩Ⅱ.求锥体的体积则()21211233V h S h h r ππ=⋅=+⋅=【例4】1.若一个四面体的所有棱长均为1,四个顶点在同一个球面上,则此球的表面积为__________.2.如图,半球内有一内接正四棱锥S ABCD -,该四棱锥的体积为3,则该半球的体积为__________.3.已知圆锥的顶点和底面圆周都在球O 的球面上,圆锥的母线长为3,侧面展开图的面积为3π,则球O 的表面积等于__________.4.以ABC 为底的两个正三棱锥P ABC -和Q ABC -内接于同一个球,并且正三棱锥P ABC -的侧面与底面ABC 所成的角为45︒,记正三棱锥P ABC -和正三棱锥Q ABC -的体积分别为1V 和2V ,则12V V =__________.5.《九章算术》是我国古代的数学名著,其中有很多对几何体体积的研究,已知某囤积粮食的容器的下面是一个底面积为32π,高为h 的圆柱,上面是一个底面积为32π,高为h 的圆锥,若该容器有外接球,则外接球的体积为__________.6.已知三棱锥P ABC -的四个顶点在球O 的球面上,PA PB PC ==,ABC △是边长为2的正三角形,E F 、分别是PA AB 、的中点,90CEF ∠=︒,则球O 的体积为__________.课堂练习4:1.正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为__________.2.底面是边长为1的正方形,侧面是等边三角形的四棱锥的外接球的体积为__________.3.已知正方体1111ABCD A B C D -的棱长为2,其各面中心分别为E F G H M N 、、、、、,则连接相邻各面中心构成的几何体的外接球表面积为__________.4.设A ,B ,C ,D 是同一个半径为4的球的球面上四点,ABC ∆为等边三角形且面积为D ABC -体积的最大值为__________.5.在正三棱锥P ABC -中,6AB BC AC ===,点D 是PA 的中点.若PB CD ⊥,则该三棱锥外接球的表面积为__________.5.其他模型问题阐述①.面ABC ⊥面BCD ;②.记12r r 、分别为ABC BCD △、△的外接圆半径,R 为三棱锥A BCD -外接球半径.①.三棱锥D ABC -中,AD 为外接球直径;②.记球面距1OO d =,ABC △的外接圆半径为r ,D ABC -的高为h .示例图像对应性质①.2h d =;②.2222124BC R r r =+-(BC 为交线长);①.AB DB AC DC ⊥⊥、(直径所对圆周角);②.222R d r =+且2h d =;解题步骤①.确定三棱锥A BCD -中的两个垂直平面;②.求出对应的外接圆半径和交线长;③.求外接球的半径;①.确定外接球的直径;②.求出底面三角形外接圆半径r ;③.22D ABC R r d h V --→→→;【示例5】1.将长、宽分别为4和3的长方形ABCD 沿对角线AC 折成直二面角,得到四面体A BCD -,则四面体A BCD -的外接球的表面积为__________.【解析】由题意,面ACD ⊥面ACB 且5AC =而ACD ACB △、△都是直角三角形,则12522AC r r ===;则2222122544AC R r r =+-=;得2425S R ππ==2.已知三棱锥S ABC -的所有顶点都在球O 的表面上,ABC △是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此三棱锥的体积为__________.【解析】在ABC △中,2sin 3AB r C ==;同时112R SC ==,则d ==,则2h d ==∴111sin 33326V hS AB AC C ==⨯⋅⋅=【例5】1.已知三棱维A BCD -中,侧面ABC ⊥底面BCD ,ABC △是边长为6的正三角形,BCD ∆是直角三角形,且2BCD π∠=,4CD =,则此三棱锥外接球的表面积为__________.2.在三棱锥A BCD -中,BA AD ⊥,BC CD ⊥,且AD ==A BCD -外接球的体积为__________.3.已知球的直径4SC =,A ,B 是该球球面上的两点,AB =,30ASC BSC ∠=∠=︒,则棱锥S ABC -的体积为__________.4.已知球的直径4SC =,A ,B 是该球球面上的两点.2AB =,45ASC BSC ∠=∠=︒,则棱锥S ABC -的体积为__________.5.已知三棱锥S ABC -外接球的球心O 在线段SA 上,若ABC △与SBC △均为面积是的等边三角形,则三棱锥S ABC -外接球的体积为__________.6.已知三棱锥S ABC -的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB ,SA AC =,SB BC =,三棱锥S ABC -的体积为9,则球O 的表面积为__________.课后作业:1.已知圆锥的底面圆周及顶点均在球面上,若圆锥的轴截面为正三角形,则圆锥的体积与球的体积之比为__________.2.已知一个圆柱的高是底面半径的2倍,且其上、下底面的圆周均在球面上,若球的体积为323π,则圆柱的体积为__________.3.已知在ABC ∆中,角A B C 、、所对的边分别为a b c 、、,且2a =,6A π=,又点A B C 、、都在球O 的球面上,且点O 到平面ABC ,则球O 的体积为__________.4.一个正三棱锥的底面边长等于一个球的半径,该正三棱锥的高等于这个球的直径,则球的体积与正三棱锥体积的比值为__________.5.正四面体A BCD -的棱长为4,点E 为BC 边上的中点,过点E 做其外接球的截面,则截面圆的面积最小值为__________.6.已知一个正三棱柱所有棱长均为3,若该正三棱柱内接于半球体,即正三棱柱的上底面的三个顶点在球面上,下底面的三个顶点在半球体的底面圆内,则该半球体的体积为__________.7.所有棱长都是3的直三棱柱111ABC A B C -的六个顶点都在同一球面上,则该球的表面积是__________.8.已知圆柱1OO 的两底面圆周上的所有点都在球C 的表面,且圆柱1OO 的底面半径为1,高为,则球C 的表面积为__________.9.已知某圆柱的轴截面为正方形,则此圆柱的表面积与此圆柱外接球的表面积之比为__________.10.已知直三棱柱111ABC A B C -的6个顶点都在球O 的球面上,若1AB =,AC =,AB AC ⊥,14AA =,则球O 的表面积为__________.11.已知正三棱台的高为1,上、下底面边长分别为和,其顶点都在同一球面上,则该球的表面积为__________.12.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为__________.13.正三棱柱111ABC A B C -内接于半径为2的球,若A ,B 两点的球面距离为π,则正三棱柱的体积为__________.14.直三棱柱111ABC A B C -的各顶点都在同一球面上,若12AB AC AA ===,120BAC ∠=︒,则此球的表面积等于__________.15.已知矩形ABCD 的顶点都在半径为2的球O 的球面上,且AB =,BC =,过点D作DE 垂直于平面ABCD ,交球O 于点E ,则棱锥E ABCD -的体积为__________.16.在三棱锥P ABC -中,PA ⊥平面ABC ,AB BC ⊥,3AB =,4BC =,5PA =,则三棱锥P ABC -的外接球的表面积为__________.17.《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥P ABC-为鳖臑,PA⊥平面ABC,2==,4PA AB-的四个顶点都在球O的球AC=,三棱锥P ABC面上,则球O的表面积为__________.18.已知在半径为2的球面上有A、B、C、D四点,若2==,则四面体ABCD的AB CD体积的最大值为().A B C.D19.已知四棱锥P ABCD=====,且底面ABCD为正方形,则-满足2PA PB PC PD AB该四棱锥的外接球的体积为__________.20.已知三棱锥P ABC -的四个顶点在球O 的球面上,PA PB PC ==,ABC ∆是边长为2的正三角形,PA PC ⊥,则球O 的体积为__________.21.高为1的圆锥内接于半径为1的球,则该圆锥的体积为__________.22.已知正四棱锥P ABCD -的高为2,AB =,过该棱锥高的中点且平行于底面ABCD的平面截该正四棱锥所得截面为1111A B C D ,若底面ABCD 与截面1111A B C D 的顶点在同一球面上,则该球的表面积为__________.23.已知正四棱锥的侧棱长为l ,其各顶点都在同一球面上.若该球的体积为36π,且3l ≤≤,则该正四棱锥体积的取值范围是__________.24.已知球O 的半径为1,四棱锥的顶点为O ,底面的四个顶点均在球O 的球面上,则当该四棱锥的体积最大时,其高为__________.25.已知四棱锥S ABCD -的所有棱长均相等,且底面是边长为的正方形,其5个顶点都在直径为10的球面上,则该四棱锥的体积为__________.26.已知1111ABCD A B C D -是边长为1的正方体,S ABCD -是高为1的正四棱锥,若点1111S A B C D 、、、、在同一球面上,则该球的表面积为__________.27.已知三棱锥S ABC -的底面是以AB 为斜边的等腰直角三角形,2SA SB SC AB ====,设S ,A ,B ,C 四点均在以O 为球心的某个球面上,则O 到平面ABC 的距离为__________.28.现有一副斜边长相等的直角三角板.若将它们的斜边AB 重合,其中一个三角板沿斜边折起形成三棱锥A BCD -,如图所示,已知6DAB π∠=,4BAC π∠=,三棱锥的外接球的表面积为4π,该三棱锥的体积的最大值为().A B C D 29.已知三棱锥A BCD -的四个顶点A ,B ,C ,D 都在球O 的表面上,BC CD ⊥,AC ⊥平面BCD ,且AC =,2BC CD ==,则球O 的表面积为__________.30.已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是__________.31.已知矩形ABCD的顶点都在半径为2的球O的球面上,且AB=,BC=,过点D 作DE垂直于平面ABCD,交球O于点E,则棱锥E ABCD-的体积为().32.已知圆锥底面圆的直径为3,圆锥的高为,该圆锥的内切球也是棱长为a的正四面2体的外接球,则此正四面体的棱长a为__________.33.设P,A,B,C为球O表面上的四个点,PA,PB,PC两两垂直,且3PB=,PA=,6三棱锥P ABC-的体积为18,则球O的体积为__________.34.已知六棱锥P ABCDEFPA=,PA⊥底面-的七个顶点都在球O的表面上,若2ABCDEF,且六边形ABCDEF是边长为1的正六边形,则球O的体积为__________.35.已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为__________.36.如图,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为O.D、∆分别是以BC,CA,AB为底边的等腰三E、F为圆O上的点,DBC∆,ECA∆,FAB角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起DBC∆,使得D、∆,FAB∆,ECAcm的最大E、F重合,得到三棱锥.当ABC△的边长变化时,所得三棱锥体积(单位:3)值为__________.37.已知底面边长为1的正四棱柱的各顶点均在同一球面上,则该球的体积为__________.38.已知S ,A ,B ,C 是球O 表面上的点,SA ⊥平面ABC ,AB BC ⊥,1SA AB ==,BC =O 的表面积等于__________.39.已知在半径为2的球面上有A 、B 、C 、D 四点,若2AB CD ==,则四面体ABCD 的体积的最大值为__________.40.已知点P A B C D 、、、、是球O 表面上的点,PA ⊥平面ABCD ,四边形ABCD 是边长为正方形.若PA =,则OAB ∆的面积为__________.41已知四面体P ABC -的外接球的球心O 在AB 上,且OP ⊥面ABC ,2AC =.若32P ABC V -=,则该球的体积为__________.。
空间锥体的外接球和内切球问题问题描述
在三维空间中,我们有一个锥体,其顶点位于原点,底面是一
个正多边形。
我们希望找到这个锥体的外接球和内切球的半径。
解决方法
为了解决这个问题,我们可以采用以下简单的方法:
1. 外接球的半径:外接球的半径等于底面正多边形边长的一半。
这是因为正多边形的顶点位于外接圆上,所以外接圆的半径等于顶
点与中心之间的距离。
2. 内切球的半径:内切球的半径等于底面正多边形边长的二分
之根号3。
这是因为正多边形的中心与内切圆的圆心重合,所以内
切圆的半径等于中心到一条边的距离。
示例
假设我们有一个底面为正六边形的锥体,边长为4个单位。
按照上述方法,我们可以计算出:
- 外接球的半径为2个单位。
- 内切球的半径为2根号3个单位。
总结
通过简单的方法,我们可以求解三维空间中锥体的外接球和内切球的半径。
这个方法适用于任意底面为正多边形的锥体,提供了一种简洁而没有法律复杂性的解决方案。
以上内容为对"空间锥体的外接球和内切球问题"的描述和解决方法。
根据问题的具体情况,可以通过计算公式得出外接球和内切球的半径。
请根据实际需求进行具体计算。
高考数学中的内切球和外接球问题---专题复习高考数学:内切球和外接球问题多面体的顶点都在同一球面上时,称该多面体为球的内接多面体,该球为多面体的外接球。
多面体外接球问题是立体几何的重点,也是高考的热点,考查学生的空间想象能力和化归能力。
解决该问题需要运用多面体和球的知识,并特别注意多面体的几何元素与球的半径之间的关系。
多面体外接球半径的求法在解题中往往起到至关重要的作用。
一、直接法(公式法)1、求正方体的外接球的有关问题例1:若正方体的棱长为3且顶点都在同一球面上,求该球的表面积。
解析:要求球的表面积,只需知道球的半径。
由于正方体内接于球,所以它的体对角线正好为球的直径,因此求球的半径可转化为先求正方体的体对角线长,再计算半径。
故表面积为27π。
例2:一个正方体的各顶点均在同一球的球面上,若该正方体的表面积为24,则该球的体积为多少?解析:要求球的体积,还需先求出球的半径。
由正方体表面积可求出棱长,从而求出正方体的体对角线长为3√3.因此,该球的半径为3,故该球的体积为36π。
2、求长方体的外接球的有关问题例1:一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱长分别为1、2、3,则该球的表面积为多少?解析:关键是求出球的半径,因为长方体内接于球,所以它的体对角线正好为球的直径。
长方体体对角线长为√14,故球的表面积为14π。
例2:已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则该球的表面积为多少?解析:正四棱柱也是长方体。
由长方体的体积16及高4可以求出长方体的底面边长为2,因此,长方体的长、宽、高分别为2、2、4.故该球的表面积为24π。
3、求多面体的外接球的有关问题例:一个底面为正六边形的六棱柱,侧棱垂直于底面,已知该六棱柱的顶点都在同一球面上,且该六棱柱的体积为8,底面周长为3,则该球的体积为多少?解析:设正六棱柱的底面边长为x,高为h。
由底面周长可得x=3/6=1/2,由体积可得h=4/3.因此,正六棱柱的底面圆的半径为√3/2,外接球的半径为√13/2.故该球的体积为(52/3)π。
几何体的外接球与内切球的有关问题一、外接球的问题简单多面体外接球问题是立体几何中的难点和重要的考点,此类问题实质是计算球的半径或确定球心O 的位置问题,其中球心的确定是关键.(一) 由球的定义确定球心球的定义:在空间中,如果一个定点与一个简单多面体的所有顶点的距离都相等,那么这个定点就是该简单多面体的外接球的球心.由上述性质,可以得到确定简单多面体外接球的球心的如下结论.结论1:正方体或长方体的外接球的球心其体对角线的中点.结论2:正棱柱的外接球的球心是上下底面中心的连线的中点.结论3:直三棱柱的外接球的球心是上下底面三角形外心的连线的中点,由球心、底面中心及底面一顶点构成的直角三角形便可得球半径.(在1BOO Rt ∆中,21212OO BO BO +=,即.)结论4:正棱锥的外接球的球心在其高上,具体位置可通过构造直角三角形利用勾股定理求得. (以正三棱锥为例:设正三棱锥的底面△ABC 的边长为a ,高为h ,外接球球心为O ,半径为R .在1AOO Rt ∆中,21212OO AO AO +=,即222)(33R h a R -+⎪⎪⎭⎫ ⎝⎛=.) 结论5:若棱锥的顶点可构成共斜边的直角三角形,则公共斜边的中点就是其外接球的球心,则公共斜边的一半就是其外接球的半径.(二)构造正方体或长方体确定球心长方体或正方体的外接球的球心是在其体对角线的中点处.1.可构造正方体的类型:①正四面体:棱长对应正方体的面对角线.①②③②三条侧棱两两垂直的正三棱锥:底面棱长对应正方体的面对角线,侧棱对应正方体的棱长.③四个面都是是直角三角形的三棱锥:最长的棱长对应正方体的体对角线.2.可构造长方体和正方体的类型①同一个顶点上的三条棱两两垂直的四面体;②三个侧面两两垂直的三棱锥;③有三个面是直角三角形的三棱锥;①与②与③④④相对的棱相等的三棱锥:设对应长方体的长、宽、高分别为a、b、c,则BC2=a2+b2,AC2=a2+c2,AB2=b2+c2. 所以对应长方体的体对角线为.⑤含有其它线面垂直关系的棱锥.(三)由性质确定球心利用球心O与截面圆圆心O’的连线垂直于截面圆,确定球心.记球的半径为R,截面圆的半径为r,球心O与截面圆圆心O’的距离为d,则有R2=r2+d 2.(四)圆柱外接球模型计算球的半径一个底面半径为r,高为h的圆柱,求它的外接球半径.(1)(2)(3)变形一:如果我们对圆柱上下底面对应位置处,取相同数量的点,比如都取三个点,如图(1)所示.我们可以得到(直)三棱柱,它的外接球其实就是这个圆柱的外接球,所以说直棱柱的外接球求半径符合这个模型. 在这里棱柱的高就是公式中的h,而棱柱底面△ABC外接圆的半径则是公式中的r.变形二:如果把三棱柱上面的C1去掉,如图(2)所示,我们得到有一个侧面⊥矩形底面的四棱锥,其中r为垂直底面的侧面△ABC的外接圆半径,h为垂直于那个侧面的底面边长AA1.变形三:如果把上面的那个三棱柱上面的B1,C1两点去掉,如图(3)所示,我们得到一根侧棱⊥底面的三棱锥,其中r为底面△ABC外接圆半径,h为垂直于底面的那条侧棱AA1.二、内切球问题若一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球.结论1:内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等.结论2:正多面体的内切球和外接球的球心重合.结论3:正棱锥的内切球和外接球球心都在高线上,但不重合.结论4:基本方法:构造三角形利用相似比和勾股定理.结论5:体积分割是求内切球半径的通用做法.(一)正方体的的内切球设正方体的棱长为a,求(1)内切球半径;(2)与棱相切的球半径.(1)内切球:截面图为正方形的内切圆,得.(2)棱切球:切点为正方体各棱的中点,截面图为为正方形的外接圆,得.(二)棱锥的内切球(分割法)将内切球的球心与棱锥的各个顶点连线,将棱锥分割成以原棱锥的面为底面,内切球的半径为高的小棱锥,根据分割前后的体积相等,列出关于半径的方程.设三棱锥的棱长为a ,内切球半径为r.V V V V V PAB O PBC O PAC O ABC O ABC P -----+++=r S r S r S r S PAB PBC PAC ABC 31313131+++= r S S S S PAB PBC PAC ABC )(31+++=所以一般地,记棱锥的体积为V ,表面积为S ,则内切球的半径为.(三)圆柱、圆锥的内切球(截面法)(1)圆柱的内切球:圆柱的轴截面为正方形,记圆柱的底面圆的半径r ,内切球的半径R ,则R =r .(2)圆锥的内切球:圆锥的轴截面为三角形的内切圆,记圆锥的底面圆的半径r ,内切球的半径R ,由于在△ABC 中,所以.备注:1.三角形内切圆的半径S S S S AOB AOC BOC ABC ∆∆∆∆++=r c b a cr br ar )(21212121++=++=所以三角形内切圆的半径为,其中S 为△ABC 的面积,C 为△ABC 的周长.2. 三角形外接圆的半径利用正弦定理,.①正三角形:,其中a 为正三角形的边长.②直角三角形:,其中c 为直角三角形的斜边.3. 正三角形的内切圆与外接圆的半径之比正三角形的内切圆与外接圆的两个圆心“二心合一”.设正三角形的边长为a ,内切圆半径为r ,外接圆半径为R.由于,a a a a a a C S r 6360sin 2122=++︒⋅⋅⋅⨯==, 所以,即圆心O 为正三角形高h 的三等分点.4. 正四面体的内切球与外接球的半径之比正四面体的内切球与外接球的两个球心“二心合一”.设正四面体A -BCD 的棱长为a ,内切球半径为r ,外接球半径为R ,则OA=OB=R ,OE=r.∵底面△BCD 为正三角形,∴BE=在BEO Rt ∆中,,即,得∴,即球心O 为正四面体高h 的四等分点.5.正三棱柱的内切球与外接球的半径之比正三棱柱的内切球与外接球的球心是重合的,过侧棱和它们的球心O 作截面如下图所示:设正三棱柱底面边长为. 由于内切球投影到底面的圆是底面正三角形的内切圆,所以,从而正三棱柱的高为.在O D A Rt 11∆中,得, 因此1:5:21=R R .。
与内切球外接球半径相关的问题有关于内切球、外接球的问题,应该说是一个比较困难的问题,几乎所有同学都会感到无从下手,这是正常的,因为这类问题需要强有力的想象力,同时方法性极强。
我们就这部分问题,尽量总结全面。
1. 内切球和外接球的基本定义;立体图形的内切球是指:与该立体图形的所有面都相切的球,注意是与所有面都相切,因此,很多立体图形是不存在内切球的。
基本性质是:球心到所有面的距离相等,且为内切球半径。
立体图形的外接球是指:立体图形的所有顶点都在球面上。
基本性质是:球心到所有顶点的距离相等,且为外接球半径。
2.长方体的外接球:长方体中从一个顶点出发的三条棱长分别为c b a ,,,则体对角线长为222c b a l ++=,几何体的外接球直径R 2,长方体体对角线长l ,则2222c b a R ++=3.正方体的外接球:正方体的棱长为a ,则正方体的体对角线为a 3,其外接球的直径R 2为a 3。
4.正四面体的内切球、外接球(1)正四面体的内切球球心和外接球球心是重合的,并且都在正四面体的高线上。
(2)正四面体的高若为h ,则外接球半径34R h =,内切球半径14r h = 5. 直棱柱的外接球:直棱柱外接球半径的思想是:找出直棱柱的外接圆柱,圆柱的外接球就是所求直棱柱的外接球。
(1) 直棱柱的体对角线长就是外接球的直径,这是核心。
(2) 直棱柱的体对角线2=底面图形的外接圆直径2+侧棱(即高)26.正棱锥的外接球:正棱锥外接球半径的思想是:球心在正棱锥的高线上,根据球心到各个顶点的距离是外接球半径,列出关于半径的方程。
我们需要考虑将“球心”“底面正多边形的中心”“底面上任一个顶点”这三个点连接起来,构成一个直角三角形,利用勾股定理,列出关于半径的方程。
一般来说这个方程是:222()h R a R -+=或222()R h a R -+=,这里的h 是指正棱锥的高,a 是指底面正多边形的对角线长的一半,若底面为正三角形时,a 是指正三角形中线长的23,考生可以划出一个图形,印证一下这些内容。
7.补体法:(1)补体法是用于求锥体的外接球半径的一种简洁方法,而且如果不使用该方法,会使问题变得非常难于解决。
(2)使用条件:一是由三条两两垂直的棱构成的锥体,可以使用补体法,这时候往往会补成长方体或正方体;二是有一条棱与底面垂直的锥体,可以将其先补成直棱柱,然后直接求棱柱的外接球,参看第5条。
(3)补体法一般是将锥体补成柱体,这样的柱体多为长方体或正方体,我们一般是先画出补成之后的图形,然后在补成之后的图形中标注出题目中所说的锥体,这样,就更清晰,即所求的锥体的外接球也就是补成之后立体图形的外接球。
8.体积分割法体积分割法是用于求锥体或柱体(多为求锥体的)内切球半径的一种非常简单的方法 对于锥体来说,1S hr S=,r 为内切球半径,1S 为锥体的底面积,h 为该锥体的高,为该锥体的全面积。
对于该公式的由来,可以类比我们初中讲过的三角形中求内切圆半径的面积分割法。
对于柱体的内切球半径求法,13S hr S=,但是这时候往往因为柱体的全面积求解比较麻烦而采取其他思路,我们需要注意,柱体的内切球必然要与上下底面相切,那么该柱体的高也就等于球的直径。
这一点很重要。
1. 已知一个正方体的所有顶点都在一个球面上,若球的体积为92π,则正方体的体积为____。
2. 平面α截球O 的球面所得圆的半径为1,球心O 到平面α为___3. 已知底面边长为1的各顶点均在同一个球面上,则该球的体积为___4. 若所有侧棱长均为1的正四面体的内切球与外接球半径分别为.r R ,求它们的比值为___5. 已知正六棱柱的12个顶点都在一个半径为3时,其高的值为_____6. 已知正四棱柱的侧棱与底面的边长都为___7. 一个三棱柱的底面为正三角形,且侧棱与底面垂直,一个体积为43π的球体与棱柱的所有面都相切,那么这个三棱柱的表面积为___8. 在直三棱柱111C B A ABC -中,4,3,6,41====AA A AC AB π,则直三棱柱111C B A ABC -的外接球的表面积_____________。
9. 正四棱锥S ABCD -点S A B C D 、、、、都在同一球面上,则此球的体积为 .10. 正四棱锥S ABCD -的底面边长为1S A B C D 、、、、都在同一球面上,则此球的体积为 .11. 正四棱锥O ABCD -的体积2O 为球心,为OA 半径的球的表面积___12. 三棱锥A BCD -中,AB ⊥平面BCD ,CD BC ⊥,3AB =,4BC =,5CD =则三棱锥A BCD -外接球的表面积为____13. 四面体ABCD 的外接球为O ,AD 与平面ABC 垂直,2AD =,Rt ABC #中,,2ACB AB π∠=则球O 的表面积为__________.14.四棱锥ABCD P -中,底面ABCD 为正方形。
ABCD PD ⊥,PD=AB=2,则ABCD P -的内切球与外接球半径分别为、。
15.已知三棱锥ABC P -,点C B A P ,,,都在半径为3的球面上,若PC PB PA ,,两两相互垂直,则球心到截面ABC 的距离为。
16.三棱柱111C B A ABC -的6个顶点都在球O 的球面上。
若12,,4,31=⊥==AA AC AB AC AB ,则球O 的半径为。
17.H 为球O 的直径AB 上一点,2:1:=HB AH ,⊥AB 平面α,H 为垂足,α截球O 所得截面的面积为π,则球O 的表面积为。
18.球的半径为2,相互垂直的两个平面分别截球面得两个圆,若两圆的公共弦长为2,则两圆的圆心距等于。
19.A 、B 、C 、D 在同一个球的球面上,,若四面体ABCD 体积的最大值为23,则这个球的表面积为______________.20.三棱锥S-ABC 的所有顶点都在球o 的球面上,△ABC 是边长为1的正三角形,SC 为球O 的直径,且SC=2,则此三棱锥的体积为______.21.三棱锥P ABC -中,PA ⊥平面ABC ,,1,AC BC AC BC PA ⊥===锥外接球的表面积为__________.22.边长为ABC 内接于体积是的球O ,则球面上的点到该三角形所在平面最大的距离是_________.23.正四面体ABCD 的棱长为4,E 为棱BC 的中点,过E 作其外接球的截面,则截面面积的最小值为_________。
24. 三棱柱侧棱垂直于底面,所有棱长都为a ,顶点在同一个球面上,则该球的表面积为_____________.25.___________。
26.一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是:( )(A )433 (B)33 (C) 43 (D) 12327.如果三棱锥的三个侧面两两垂直,它们的面积分别为62cm 、42cm 和32cm ,那么它的外接球的体积是 。
参考答案1.分析:设出正方体棱长,利用正方形的体对角线就是外接球的直径,通过球的体积求出正方体的棱长.解答:解:因为正方体的体对角线就是外接球的直径,设正方体的棱长为a ,所以正方体的.(1)球的体积为:34932ππ⨯=⎝⎭,解得a =2.解:因为平面α截球O 的球面所得圆的半径为1,球心O 到平面α=体积易求为.3.试题分析:根据正四棱柱的几何特征得:该球的直径为正四棱柱的体对角线,故2=,即得1R =,所以该球的体积224441333V R πππ===.4.每个正三棱锥体积113V Sr =,而正四面体PABC 体积()213V S R r =⨯⨯+,根据前面的分析,124V V ⨯=,()1114333r S r S R r R ∴⨯⨯⨯=⨯⨯+∴=.6.正四棱锥的各个顶点到它的底面的中心的距离都为3,∴正四棱锥外接球的球心在它的底面的中心,且球半径3r =,球的表面积2436S r ππ==,因此,本题正确答案是:36π.7.解:此棱柱为正棱柱,体积43π的球体半径为1,由此可以得到三棱柱的高为2,底面三角形内切圆的半径为1,故底面三角形高为3,边长为,所以表面积123322S =⨯⨯+⨯=因此,本题正确答案是:8.由213O ABCD V AB ON -=∙可得,2ON =,在ONA ∆中,2226OA ON NA =+=.故球的表面积2424S OA ππ=∙=.由已知条件可知,以,,PA PB PC 为棱的正三棱锥可以补充成球的内接正方体,故而()22222PA PB PC R ++=,由已知PA PB PC ==,得到2PA PB PC ===.因为?1133P ABC ABC PBC A PBCV V h S PA S -∆∆-=∙=∙,得到23h =故而球心到截面ABC 的距离为3R h -=. 如图所示,球心o 即为侧面11BCC B 对角线的交点。
设BC 的中点为M ,连接OM ,AM ,即可知OM ⊥平面ABC ,连接AO ,则可知6OM =,52AM =,在Rt AOM ∆中,由勾股定理得球O 的半径132R =. 14.又由题意得2rππ=,则1r =,故22113RR ⎛⎫=+ ⎪⎝⎭,即298R =.由球的表面积公式,得2942S Rππ==.15.如图,2.DE 为两圆的公共弦,点B 为弦的中点,因为OD 与OE 均为球的半径,所以OD =2,所以OB DE ⊥,因为2DE =,所以OB ==所以AB BC ⊥,四边形OABC 是矩形,所以圆心距AC OB ==3.16.ABC ∆中,AB BC ==2AC =,222AC AB BC =+,2ABC π∠=,截面小圆的半径112r AC ==,四面体A B C 体积的最大值为23,1112223323D ABCV S ABC h h h -=∆*=***=∴=。
设球的半径为R ,球心为O ,O 到截面的距离为d 。
当D 到底面ABC 距离最远,即h R d =+时,四面体ABCD 体积的最大值。
d == 22R R==-,22144R R R -=-+,解得54R =∴这个球的表面积为2252544164R πππ=*=。
4.17.分析试题:几何问题的解决一般依赖于图形,作出三棱锥S ABC -,如下图,O 是SC 中点,由于SC 是球的直径,A 、B 在球面上,故SB BC ⊥,SA AC ⊥.设H 是等边ABC∆的中心,则OH ⊥平面ABC ,ABC ∆是边长为1的正三角形,则S ABC ∆=CH =,又1OC =,则OH ===,O 是SC 的中点,∴点S 到平面ABC 的距离为23OH =11233436S ABCV S ABC OH -=∆∙=∙∙=。