《医用物理学》振动和波

第八章 振动和波通过复习后，应该:1.掌握简谐振动方程、波的产生和传播、波动方程、波的能量和强度、波的干涉;2.理解简谐振动的能量、简谐振动的合成、惠更斯原理、波的衰减;3.了解衰减振动、受迫振动、共振、复杂振动的分解、驻波。

8-1 试解释下列名词:简谐振动、振幅、频谱分析、基频、频谱图、波动、横波、纵波、波阵面、波的强度。

答: ①简谐振动:质点在弹性力（或准弹性力）作用下所作的振动叫简谐振动，其加速度与离开平衡位置的位移成正比，且方向相反。

②振幅:振动物体离开平衡位置的最大距离称为振幅。

③频谱分析:将任一周期性振动分解为多个简谐振动之和的过程，称为频谱分析。

④基频:一个复杂的振动可以分解为若干个频率不同的简谐振动之和，这些分振动频率中最低的频率称为基频，它与原振动的频率相同。

⑤频谱图:将组成一个复杂振动的各分振动的频率和振幅找出来，按振幅与频率关系列出谱线，这种图称为频谱图。

⑥波动:振动在介质中的传播现象叫波动，它也是一种重要的能量传播过程。

其中简谐振动在介质中传播所形成的波叫简谐波。

⑦横波:波在介质中传播时，如果介质中各质点振动的方向与波的传播方向垂直，则该波叫做横波。

⑧纵波:如果介质中各质点振动的方向与波的传播方向相互平行，则这种波称为纵波。

⑨波阵面:在波传播的介质中，质点振动相位相同的各点连成的面称为波阵面。

⑩波的强度:单位时间内通过垂直于波的传播方向单位面积上的平均能量，称为波的强度。

8-2 有一质点作简谐振动，试分析它在下列位置时的位移、速度、加速度的大小和方向:①平衡位置，向正方向运动;②平衡位置，向负方向运动;③正方向的端点;④负方向的端点。

解: 设该质点的振动方程为:)cos(ϕω+=t A x将它对时间t 分别求一阶导数、二阶导数，可得到速度v 和加速度a 的表达式:)2cos()sin(πϕωωϕωω++=+-==t A t A dt dx v)cos()cos(2222πϕωωϕωω++=+-==t A t A dtx d a 由此可以看出，速度的相位超前位移2π，加速度与位移的相位相反。

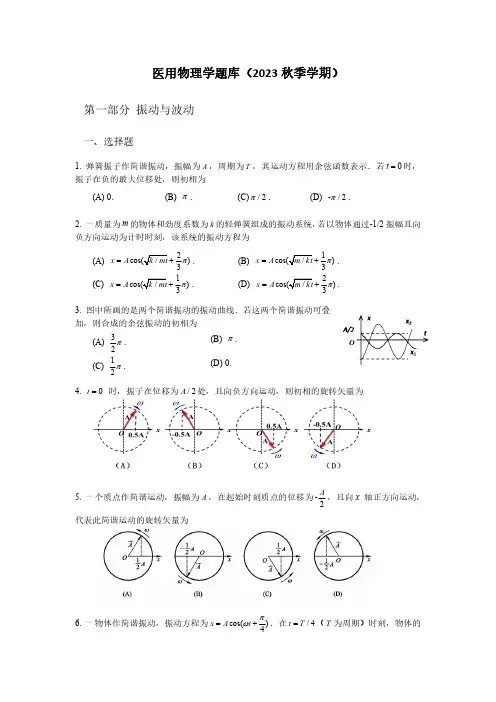
医用物理学题库（2023秋季学期）第一部分振动与波动一、选择题1.弹簧振子作简谐振动，振幅为A ，周期为T ，其运动方程用余弦函数表示．若0t =时，振子在负的最大位移处，则初相为(A)0．(B)π．(C)/2π．(D)-/2π．2.一质量为m 的物体和劲度系数为k 的轻弹簧组成的振动系统，若以物体通过-1/2振幅且向负方向运动为计时时刻，该系统的振动方程为(A)2)3x A π=+.(B)1)3x A π=+.(C)1)3x A π=+.(D)2)3x A π=+.3.图中所画的是两个简谐振动的振动曲线．若这两个简谐振动可叠加，则合成的余弦振动的初相为(A)32π.(B)π.(C)12π.(D)0.4.0t =时，振子在位移为/2A 处，且向负方向运动，则初相的旋转矢量为5.一个质点作简谐运动，振幅为A ，在起始时刻质点的位移为-2A ，且向x 轴正方向运动，代表此简谐运动的旋转矢量为6.一物体作简谐振动，振动方程为cos(4x A t πω=+．在/4t T =（T 为周期）时刻，物体的加速度为(A)222A ω-．(B)222A ω．(C)232A ω-．(D)232A ω．7.一物体作简谐振动，振动方程为1cos()4x A t ωπ=+．在/2t T =（T 为周期）时刻，物体的加速度为(A)222A ω-．(B)222A ω．(C)232A ω-．(D)232A ω．8.已知某简谐运动的振动曲线如图所示，则此简谐运动的运动方程为(A)222cos[]33x t ππ=-.(B)222cos[]33x t ππ=+.(C)422cos[]33x t ππ=-.(D)422cos[]33x t ππ=+.9.一质点作简谐振动，已知振动周期为T ，则其振动动能变化的周期是(A)4T ．(B)2T ．(C)T ．(D)2T ．10.一弹簧振子作简谐振动，当位移为振幅的一半时，其动能为总能量的(A)14．(B)12．(C)12．(D)34．11.一质点作简谐振动，已知振动频率为f ，则振动动能的变化频率是(A)4f ．(B)2f ．(C)f ．(D)2f ．12.两个同振动方向、同频率、振幅均为A 的简谐运动合成后，振幅为2A ，则这两个简谐运动的相位差为(A)3π．(B)2π．(C)π．(D)2π13.右图中所画的是两个简谐振动的振动曲线.这两个简谐振动的相位相差为(A)3π．(B)2π．(C)π．(D)014.两个同振动方向、同频率、振幅均为A 的简谐运动合成后，振幅仍为A ，则这两个简谐运动的相位差为(A)60 ．(B)90 ．(C)120 ．(D)180 .15.两个同周期简谐振动曲线如图所示．1x 的相位比2x 的相位(A)落后2π.(B)超前2π.(C)落后π.(D)超前π.16.若一平面简谐波的表达式为)cos(Cx Bt A y -=，式中A 、B 、C 为正值常量，则(A)波速为C ．.(B)周期为1/B .(C)波长为2/C π.(D)角频率为2/B π.17.一横波以速度u 沿x 轴负方向传播，t 时刻波形曲线如图所示，则该时刻(A)A 点相位为π.(B)B 点静止不动.(C)C 点相位为3/2π.(D)D 点向上运动.18.在简谐波传播过程中，沿传播方向相距为12λ(λ为波长)的两点的振动速度必定(A)大小相同，而方向相反.(B)大小和方向均相同．.(C)大小不同，方向相同．(D)大小不同，而方向相反．19.以下条件中，不属于两列相干波所必须满足的条件.(A)频率相同.(B)振动方向相同．.(C)振幅相同．(D)相位差恒定．20.如图所示，两列波长为λ的相干波在P 点相遇．波在1S 点振动的初相是1φ，1S 到P 点的距离是1r ；波在2S 点的初相是2φ，2S 到P 点的距离是2r ，以k 代表零或正、负整数，则P 点是干涉极大的条件为：(A)21r r k λ-=．(B)212k φφπ-=．(C)21212()/2r r k φφπλπ-+-=．(D)21122()/2r r k φφπλπ-+-=．20.一平面简谐波的表达式为cos(/2) (m)y t x πππ=--，则下列选项中关于该平面波描述正确的是：(A)波长= m λπ．(B)周期2T =s ．(C)频率=1νHz ．(D)波速2u =m/s.22.如图(a)表示0t =时的简谐波的波形图，波沿x 轴正方向传播，图(b)为一质点的振动曲线.则图(a)中所表示的0x =处质点振动的初相位与图(b)所表示的振动的初相位分别为(A)均为2π(B)均为2π-.(C)2π与2π-.(D)2π-与2π.23.频率为100Hz ，传播速度为300m/s 的平面简谐波，波线上距离小于波长的两点振动的相位差为/3π，则此两点相距(A)2.86m ．(B)2.19m ．(C)0.5m ．(D)0.25m ．24.平面简谐机械波在弹性介质中传播时,在传播方向上某介质元在负的最大位移处,则它的能量是(A)动能为零,势能最大(B)动能为零,势能为零(C)动能最大,势能最大(D)动能最大,势能为零25.一平面简谐波在弹性介质中传播,在介质元从最大位移处回到平衡位置的过程中(A)它的势能转换成动能(B)它的动能转换成势能(C)它从相邻的一段介质元中获得能量,其能量逐渐增大(D)它把自己的能量传给相邻的一介质元,其能量逐渐减小26.已知在某一介质中两列相干的平面简谐波的强度之比是421=I I ，则这两列波的振幅之比21A A 是(A)4(B)2(C)16(D)827.人耳能分辨同时传来的不同声音,这是由于(A)波的反射和折射(B)波的干涉(C)波的独立传播特性(D)波的强度不同28.两初相位相同的相干波源,在其叠加区内振幅最小的各点到两波源的波程差等于(A)波长的偶数倍(B)波长的奇数倍(C)半波长的偶数倍(D)半波长的奇数倍29.当超声波经过声阻抗差值较大的介质形成界面时，(A)穿透力增强.(B)分辨率增强.(C)被反射的声能增多.(D)被吸收的声能增多.30.低语时声强为10-⁸W·m -²,飞机发动机的噪声声强为10-¹W·m -²,当其频率为1000Hz 时，则它们的声强级之差为：(A)10-⁶dB.(B)150dB.(C)110dB.(D)70dB.31.一机车汽笛频率为750Hz,机车以时速90公里远离静止的观察者.观察者听到的声音的频率是(设空气中声速为340m·s -¹):(A)810Hz.(B)699Hz.(C)805Hz.(D)695Hz二、填空题1.一弹簧振子作简谐振动，振幅为A ，周期为T ，其运动方程用余弦函数表示．若0t =时，振子在负的最大位移处，则初相为_____________；振子在平衡位置向正方向运动，则初相为____________；振子在位移为/2A 处，且向负方向运动，则初相为_____．2.一质点沿x 轴作简谐振动，振动范围的中心点为x 轴的原点.若0t =时质点过0x =处且朝x 轴负方向运动，则振动的初相位0ϕ=；若0t =时质点处于/2x A =处且向x 轴正方向运动，则振动的初相位0ϕ=．3.在简谐波的一条射线上，相距0.2m 两点的振动相位差为6/π．又知振动周期为0.4s ，则波速为.4.一简谐振动的表达式为cos(3)x A t φ=+，已知0t =时的初位移为0.04m ，初速度为0.09m/s ，则振幅A =_____________，初相φ=________________．5.一弹簧振子，弹簧的劲度系数为k ，重物的质量为m ，则此系统的固有振动周期为．6.当质点以频率ν作简谐振动时，它的动能和势能的变化频率均为，总能量保持不变.7.横波的一个波长指的是波线上相邻两同相点之间的距离；一平面简谐横波的波源简谐运动的周期为T ，则2T 内波形向前推进了个波长.8.已知平面简谐波的表达式为cos()y A Bt Cx =-式中,,A B C 为正值常量，此波的波长是___，波速是______．在波传播方向上相距为d 的两点的振动相位差是________．9.在同一媒质中两列频率相同的平面简谐波的强度之比12/16I I =，则这两列波的振幅之比是12/A A =____________________．10.两相干波源S 1和S 2的振动方程分别是1cos()y A t ωϕ=+和2cos()y A t ωϕ=+.S 1距P 点3个波长，S 2距P 点4.5个波长．设波传播过程中振幅不变，则两波同时传到P 点时的合振幅是________________．11.引起人耳听觉的声波频率范围是（），频率高于20000Hz 的机械波叫（），频率低于20Hz 的机械波叫（）。

一、符号及意义相关关系：TυλυT λu T πω12====波在介质中的传播速度只与介质的性质有关二、平面简谐波的波动方程假设波沿x 轴正方向传播最基本的一个公式：位于原点处的质点的振动方程)cos(ϕω+=t A y 要做到能灵活地对其进行变形位于x 处的质点的振动方程])(cos[ϕω+-=u x t A y (可以这样理解：在原点振动时间ux 之后该点开始振动,即时间t 需要减去ux ) 然后将t 值固定为0t ，即得到了0t 时间的波形函数：])(cos[0ϕω+-=ux t A y将πυT πω22==和uT =λ带入])(cos[ϕω+-=uxt A y 式中 得到本章一个重要的方程：])(2cos[])(2cos[ϕλυπϕλπ+-=+-=xt A x T t A y (如果能准确地记住这个式子，本句以上内容可忽略)三、波的能量能量密度：单位体积中的能量能量密度w 在一个周期内的平均值称为平均能量密度w22222221υρπωρA A w ==能流：单位时间内通过介质中某一面积的能量垂直于波速方向上取面积ΔS ，平均能流为：S uA S u w P ∆=∆=2221ωρ 波的强度即平均能流密度为：2221ωρuA u w S P I ==∆=考察的一般套路：1给出某质点处于波峰或波谷的两个时间，求其周期这类题要注意的是在这两个时间点之间可能过了无数个周期 2给出振动方程求该质点作简谐运动的最大速度 对该方程求关于t 的倒数即可 3给出各种奇怪的条件让你求方程 具体问题具体分析4再有就是对波的能量的一些概念的考察 需要对提及到的概念要达到理解掌握 另外解每道题时要注意下该波的传播方向(本文中有一些是个人见解，若有不正确处请指正)。