正态分布公式推导

正态分布的分布函数公式推导正态分布是一种常见的概率分布，也称为高斯分布。

其概率密度函数为：$$f(x)=dfrac{1}{sigmasqrt{2pi}}e^{-frac{(x-mu)^2}{2sigma^2} }$$其中，$mu$是均值，$sigma$是标准差。

正态分布的分布函数可以通过积分得到，具体推导过程如下：$$F(x)=int_{-infty}^x f(t)dt$$将$f(t)$代入上式得到：$$F(x)=int_{-infty}^xdfrac{1}{sigmasqrt{2pi}}e^{-frac{(t-mu)^2}{2sigma^2}}dt$$ 对$t-mu$进行代换，令$u=dfrac{t-mu}{sigma}$，则有：$$F(x)=int_{-infty}^{frac{x-mu}{sigma}}dfrac{1}{sqrt{2pi}}e^{-frac{u^2}{2}}du$$注意到上式为正态分布的标准正态分布函数，即均值为0，标准差为1的正态分布。

标准正态分布的分布函数没有解析解，但是可以通过数值计算或查表得到。

因此，正态分布的分布函数可以通过标准正态分布的分布函数进行转换。

具体地，设$Z$为标准正态分布的随机变量，则有：$$F(x)=P(Xle x)=P(mu+sigma Zle x)=P(Zledfrac{x-mu}{sigma})=Phi(dfrac{x-mu}{sigma})$$其中，$Phi(z)$表示标准正态分布的分布函数，也称为累积分布函数。

因此，正态分布的分布函数可以表示为：$$F(x)=dfrac{1}{2}[1+mathrm{erf}(dfrac{x-mu}{sigmasqrt{2}}) ]$$其中，$mathrm{erf}(z)$为误差函数，定义为：$$mathrm{erf}(z)=dfrac{2}{sqrt{pi}}int_0^z e^{-t^2}dt$$ 综上所述，正态分布的分布函数可以通过标准正态分布的分布函数进行转换，最终得到误差函数的表达式。

正态分布的概率公式正态分布（Normal distribution），也称为高斯分布（Gaussian distribution），是一个广泛应用于自然和社会科学中的概率分布。

它被称为正态分布是因为它的概率密度函数在曲线图上呈现为一个钟形曲线，其均值和中位数相等，对称于均值。

$$f(某) = \frac{1}{\sigma\sqrt{2\pi}}\ e^{-(某-\mu)^2/2\sigma^2}$$其中，$\mu$ 是均值，$\sigma$ 是标准差，$e$ 是自然常数的底数，$某$ 是随机变量的取值。

这个公式告诉我们的是，在正态分布中，每个取值$某$所对应的概率密度是多少。

这种密度的形状是钟形曲线，它的峰值位于均值处，标准差越小，曲线越陡峭，反之曲线越平缓。

峰值处的高度由于函数式中分母中的$\sqrt{2\pi} \sigma$因子决定，在峰值处为$f(\mu) =\frac{1}{\sqrt{2\pi} \sigma}$。

这意味着正态分布的总面积为1。

标准正态分布的概率密度函数可以用以下公式表示：$$f(z) = \frac{1}{\sqrt{2\pi}}\ e^{-z^2/2}$$其中，$z = \frac{某-\mu}{\sigma}$，表示标准正态分布离均值有多少标准差。

我们可以使用标准正态分布的概率密度函数来计算一个正态分布内某个区间的概率。

具体来说，如果我们要求标准正态分布在一个区间$[a,b]$中的概率，我们可以计算：$$P(a < Z < b) = \int_a^b f(z)\ dz$$同样的，如果我们要求正态分布在一个区间$[a,b]$中的概率，我们可以将其标准化为一个标准正态分布：$$P(a < X < b) = P\left(\frac{a-\mu}{\sigma} < Z < \frac{b-\mu}{\sigma}\right)$$然后使用标准正态分布的概率密度函数计算该区间的概率。

多元正态分布公式学习多元正态分布的数学公式多元正态分布是统计学中常用的一种概率分布，它是一组随机变量的连续概率分布。

通过对多元正态分布的数学公式的学习，可以更好地理解和应用多元正态分布的相关知识。

本文将介绍多元正态分布的概念和性质，以及其数学公式的推导和应用。

1. 多元正态分布的概念和性质多元正态分布是指在多个随机变量同时服从正态分布的情况下，各个随机变量之间相互独立。

它有以下几个重要性质：（1）期望向量：多元正态分布的期望向量表示各个随机变量的均值，记作μ，即μ=(μ1, μ2, … , μn)。

（2）协方差矩阵：多元正态分布的协方差矩阵表示各个随机变量之间的相关性，记作Σ，即Σ=(σij)。

（3）概率密度函数：多元正态分布的概率密度函数是一个多元高斯函数，表示了各个随机变量在不同取值下的概率。

2. 多元正态分布的数学公式推导多元正态分布的数学公式可以通过高等数学的知识进行推导。

假设有一个n维向量X=(X1, X2, … , Xn)服从多元正态分布，其概率密度函数为：f(x)=1/[(2π)^(n/2) |Σ|^(1/2)] exp{-1/2 (x-μ)' Σ^(-1) (x-μ)}其中, x=(x1, x2, … , xn)为实际观测的取值向量。

3. 多元正态分布的应用多元正态分布的数学公式在实际应用中具有广泛的应用价值。

以下是几个常见的应用场景：（1）金融风险管理：多元正态分布可以用来对股票、债券等金融资产的价格变动进行建模和研究，从而对风险进行评估和管理。

（2）经济数据分析：多元正态分布可以用来对经济数据中的变量之间的关系进行建模和分析，从而揭示经济规律。

（3）质量控制：多元正态分布可以用来对产品质量的多个指标进行建模和分析，从而帮助企业提高产品质量。

4. 总结通过对多元正态分布的学习，我们可以了解其概念和性质，推导出其数学公式，并了解多元正态分布在实际应用中的价值。

多元正态分布是统计学中重要的概率分布之一，深入理解其原理和应用对于我们进行数据分析和建模具有重要意义。

正态分布normal distribution正态分布一种概率分布。

正态分布是具有两个参数μ和σ2的连续型随机变量的分布，第一参数μ是服从正态分布的随机变量的均值，第二个参数σ2是此随机变量的方差，所以正态分布记作N(μ，σ2 )。

服从正态分布的随机变量的概率规律为取与μ邻近的值的概率大，而取离μ越远的值的概率越小；σ越小，分布越集中在μ附近，σ越大，分布越分散。

正态分布的密度函数的特点是：关于μ对称，在μ处达到最大值，在正（负）无穷远处取值为0，在μ±σ处有拐点。

它的形状是中间高两边低，图像是一条位于x轴上方的钟形曲线。

当μ＝0，σ2 ＝1时，称为标准正态分布，记为N（0，1）。

μ维随机向量具有类似的概率规律时，称此随机向量遵从多维正态分布。

多元正态分布有很好的性质，例如，多元正态分布的边缘分布仍为正态分布，它经任何线性变换得到的随机向量仍为多维正态分布，特别它的线性组合为一元正态分布。

正态分布最早由A.棣莫弗在求二项分布的渐近公式中得到。

C.F.高斯在研究测量误差时从另一个角度导出了它。

P.S.拉普拉斯和高斯研究了它的性质。

生产与科学实验中很多随机变量的概率分布都可以近似地用正态分布来描述。

例如，在生产条件不变的情况下，产品的强力、抗压强度、口径、长度等指标；同一种生物体的身长、体重等指标；同一种种子的重量；测量同一物体的误差；弹着点沿某一方向的偏差；某个地区的年降水量；以及理想气体分子的速度分量，等等。

一般来说，如果一个量是由许多微小的独立随机因素影响的结果，那么就可以认为这个量具有正态分布（见中心极限定理）。

从理论上看，正态分布具有很多良好的性质，许多概率分布可以用它来近似；还有一些常用的概率分布是由它直接导出的，例如对数正态分布、t分布、F分布等。

正态分布应用最广泛的连续概率分布，其特征是“钟”形曲线。

附：这种分布的概率密度函数为：（如右图）正态分布公式正态分布1.正态分布：若已知的密度函数（频率曲线）为正态函数（曲线）则称已知曲线服从正态分布，记号～。

正态分布公式正态分布也称为高斯分布或正常分布，它是一种概率分布，用于描述符合几种基本假设的连续随机变量的分布。

正态分布是一个重要的基本分布，被广泛应用于统计学、自然科学、社会科学等领域中。

正态分布有许多不同的形式，但最常见的是标准正态分布。

标准正态分布的分布函数和概率密度函数分别如下：标准正态分布的分布函数：$$\\Phi (x)=\\frac{1}{\\sqrt{2\\pi}}\\int_{-\\infty}^x e^{-\\frac{t^2}{2}} dt$$标准正态分布的概率密度函数：$$\\phi (x)=\\frac{1}{\\sqrt{2\\pi}}e^{-\\frac{x^2}{2}}$$其中，$\\phi(x)$表示在点$x$处获得概率密度的值，$\\Phi(x)$表示在$-\\infty$到$x$的积分所得到的累积概率。

对于非标准正态分布，可以使用变换将其转换为标准正态分布。

转换的方法是，对于一个均值为$\\mu$，标准差为$\\sigma$的正态分布$X$，使用以下公式进行变换：$$Z=\\frac{X-\\mu}{\\sigma}$$其中，$Z$表示标准正态分布的变量。

只要确定了$Z$，就可以使用标准正态分布的表格或统计软件来计算概率。

正态分布的形状是钟形曲线，均值$\\mu$位于曲线中心，标准差$\\sigma$决定曲线的宽度。

它具有很多特性：1. 正态分布的均值、中位数和众数相等。

2. 曲线在均值处对称，即左右两侧面积相等。

3. 由于标准差的不同，曲线的高度、峰度和尖度也不同。

4. 68%的数据落在均值$\\pm$1个标准差范围内，95%的数据落在均值$\\pm$2个标准差范围内。

正态分布在现实生活中具有重要意义，例如身高、体重、智力、化学反应速率、股票收益率等，往往都服从于正态分布。

因此，深入理解正态分布的公式和性质，对于数据分析、统计学、金融学等领域的人士来说是非常重要的。

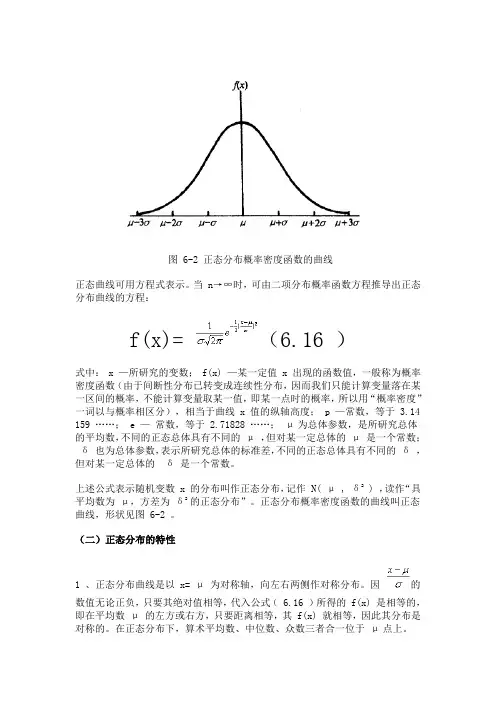
图 6-2 正态分布概率密度函数的曲线正态曲线可用方程式表示。

当n→∞时，可由二项分布概率函数方程推导出正态分布曲线的方程：f(x)= （6.16 ）式中： x —所研究的变数； f(x) —某一定值 x 出现的函数值，一般称为概率密度函数（由于间断性分布已转变成连续性分布，因而我们只能计算变量落在某一区间的概率，不能计算变量取某一值，即某一点时的概率，所以用“概率密度”一词以与概率相区分），相当于曲线 x 值的纵轴高度； p —常数，等于 3.14 159 ……； e —常数，等于 2.71828 ……；μ为总体参数，是所研究总体的平均数，不同的正态总体具有不同的μ ，但对某一定总体的μ 是一个常数；δ 也为总体参数，表示所研究总体的标准差，不同的正态总体具有不同的δ ，但对某一定总体的δ 是一个常数。

上述公式表示随机变数 x 的分布叫作正态分布，记作N( μ , δ2 ) ，读作“具平均数为μ，方差为δ2 的正态分布”。

正态分布概率密度函数的曲线叫正态曲线，形状见图 6-2 。

（二）正态分布的特性1 、正态分布曲线是以x= μ 为对称轴，向左右两侧作对称分布。

因的数值无论正负，只要其绝对值相等，代入公式（ 6.16 ）所得的 f(x) 是相等的，即在平均数μ 的左方或右方，只要距离相等，其 f(x) 就相等，因此其分布是对称的。

在正态分布下，算术平均数、中位数、众数三者合一位于μ点上。

2 、正态分布曲线有一个高峰。

随机变数 x 的取值范围为（ - ∞，+ ∞ ），在（ - ∞ ，μ ）正态曲线随 x 的增大而上升，；当 x= μ 时， f(x) 最大；在（μ ，+ ∞ ）曲线随 x 的增大而下降。

3 、正态曲线在︱x-μ︱=1 δ 处有拐点。

曲线向左右两侧伸展，当x →± ∞ 时，f(x) →0 ，但 f(x) 值恒不等于零，曲线是以 x 轴为渐进线，所以曲线全距从 -∞到+ ∞。

正态分布公式推导
正态分布叠加公式是：x+y~n(3，8)。

相互立的正态变量之线性组合服从正态分布。

即x~n(u1，(q1)^2)，y~n(u2，(q2)^)。

则z=ax+by~n(a*u1+b*u2，
(a^2)*(q1)^2+(b^2)*(q2)^2)
集中性：正态曲线的高峰位于正中央，即均数所在的位置。

对称性：正态曲线以均数为中心，左右等距，曲线两端永远不与横轴平行。

均匀变动性：正态曲线由均数所在处开始，分别向左右两侧逐渐均匀下降。

曲线与横轴间的面积总等同于1，相等于概率密度函数的函数从正无穷至负无穷分数的概率为1。

即为频率的总和为%。

两个正态分布的任意线性组合仍服从正态分布（可通过求两个正态分布的函数的分布证明），此结论可推广到n个正态分布。

因此，只需求x-3y的期望方差就可知道具体服从什么正态分布了。

标准正态分布计算公式标准正态分布是统计学中常用的一种分布，也叫做正态分布或高斯分布。

它在自然界、社会科学和工程领域中广泛应用，因为许多随机变量可以近似地服从该分布。

标准正态分布的计算公式是一个关键的工具，可以帮助我们计算出各种随机变量的概率和统计指标。

标准正态分布的计算公式如下：f(x) = (1 / √(2πσ^2)) * e^(-(x-μ)^2 / (2σ^2))在这个公式中，f(x)代表了随机变量X取值为x的概率密度函数。

μ代表期望值，表示随机变量X的平均值。

σ代表标准差，表示X的离散程度。

e是一个常数，约等于2.718。

这个公式可以帮助我们计算出标准正态分布中特定取值x的概率密度。

概率密度是指随机变量落在某个特定区间的概率，也可以理解为该区间内的单位长度上的概率。

为了更好地理解标准正态分布的计算公式，我们可以通过一个具体的例子进行说明。

假设我们有一个随机变量X，它服从标准正态分布。

我们想要计算X取值在-1和1之间的概率。

首先，我们需要计算出期望值μ和标准差σ。

在标准正态分布中，期望值μ等于0，标准差σ等于1。

然后，将这些值代入标准正态分布的计算公式中：f(x) = (1 / √(2πσ^2)) * e^(-(x-μ)^2 / (2σ^2))= (1 / √(2π*1^2)) * e^(-(x-0)^2 / (2*1^2))= 1 / √(2π) * e^(-x^2 / 2)现在我们可以将x的取值带入计算公式。

在这个例子中，x的取值范围是-1到1。

当x = -1时，我们有：f(-1) = 1 / √(2π) * e^(-(-1)^2 / 2)= 1 / √(2π) * e^(-1/2)当x = 1时，我们有：f(1) = 1 / √(2π) * e^(-1/2)通过计算，我们可以得到x取值在-1和1之间的概率密度。

此外，我们还可以使用标准正态分布的计算公式计算其他统计指标，比如平均值、方差和标准差。

第1篇一、引言正态分布是一种常见的概率分布，广泛应用于统计学、概率论等领域。

在正态分布中，方差是衡量数据离散程度的重要指标。

本文将对正态分布方差的计算方法进行详细阐述，包括公式推导、实例分析以及在实际应用中的注意事项。

二、正态分布及其参数正态分布，也称为高斯分布，是一种连续概率分布。

其概率密度函数为：f(x) = (1/√(2πσ^2)) e^(-(x-μ)^2 / (2σ^2))其中，μ为正态分布的均值，σ为正态分布的标准差。

正态分布的密度函数图像呈钟形，对称于均值μ。

三、正态分布方差计算公式正态分布的方差σ^2是衡量数据离散程度的重要指标，其计算公式如下：σ^2 = E[(x - μ)^2]其中，E为期望值，x为随机变量。

对于正态分布，方差的计算公式可以进一步简化为：σ^2 = Var(x)其中，Var(x)表示随机变量x的方差。

四、方差公式推导为了推导正态分布方差的计算公式，首先需要了解方差的定义。

方差是随机变量与其期望值之差的平方的期望值，即：Var(x) = E[(x - E(x))^2]对于正态分布，期望值E(x)等于均值μ，因此上式可以写为：Var(x) = E[(x - μ)^2]接下来，利用正态分布的概率密度函数进行推导：Var(x) = ∫(x - μ)^2 f(x) dx将正态分布的概率密度函数代入上式，得到：Var(x) = ∫(x - μ)^2 (1/√(2πσ^2)) e^(-(x-μ)^2 / (2σ^2)) dx为了方便计算，对上式进行变量替换，令t = (x - μ)^2 / (2σ^2)，则：dt = (1/σ^2) dx代入上式，得到：Var(x) = ∫2σ^2 t (1/√(2πσ^2)) e^(-t) dt简化后得到：Var(x) = 2σ^2 ∫t (1/√(2π)) e^(-t) dt利用积分公式∫t e^(-t) dt = -e^(-t) + C，其中C为积分常数，得到：Var(x) = 2σ^2 [-e^(-t) + C]由于积分上下限为0，因此C = 0，得到：Var(x) = 2σ^2 [-e^(-0) + 1]化简后得到：Var(x) = 2σ^2 [1 - 1] = 0由此可见，正态分布的方差σ^2为0，与实际情况不符。

正态分布的所有公式正态分布是一种在统计学中非常重要的概率分布，它在自然科学、社会科学以及工程技术等领域都有着广泛的应用。

咱们先来说说正态分布的概率密度函数公式，这可是理解正态分布的核心哟！它的表达式是：$f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x -\mu)^2}{2\sigma^2}}$这里的$\mu$是均值，也就是正态分布的中心位置；$\sigma$是标准差，它决定了分布的宽度。

咱们举个例子来理解一下哈。

比如说咱们要研究一个班级学生的考试成绩，假设成绩符合正态分布。

如果均值$\mu$是 80 分，标准差$\sigma$是 10 分。

那这意味着大部分同学的成绩会在 80 分左右，离80 分越远，人数就越少。

比如说 90 分以上和 70 分以下的同学相对就比较少啦。

再来说说正态分布的累积分布函数公式，它可以用来计算随机变量小于等于某个值的概率。

公式是：$F(x) = \frac{1}{2} [1 + erf(\frac{x - \mu}{\sigma \sqrt{2}})]$这里的$erf$是误差函数。

想象一下哈，还是那个班级成绩的例子。

如果咱们想知道成绩小于等于 75 分的同学所占的比例，就可以用这个累积分布函数来算一算。

正态分布还有一些重要的性质和公式。

比如，正态分布的期望就是均值$\mu$，方差就是$\sigma^2$。

这两个公式可重要啦，能帮助我们更好地描述数据的集中趋势和离散程度。

还有个有趣的现象，正态分布的 3$\sigma$原则。

大概 68%的数据会落在均值$\pm 1\sigma$的范围内，约 95%的数据会落在均值$\pm2\sigma$的范围内，而几乎 99.7%的数据会落在均值$\pm 3\sigma$的范围内。

就像前面说的那个班级，大约 68%的同学成绩会在 70 分到 90 分之间（80$\pm$10），约 95%的同学成绩会在 60 分到 100 分之间（80$\pm$20），几乎 99.7%的同学成绩会在 50 分到 110 分之间（80$\pm$30）。

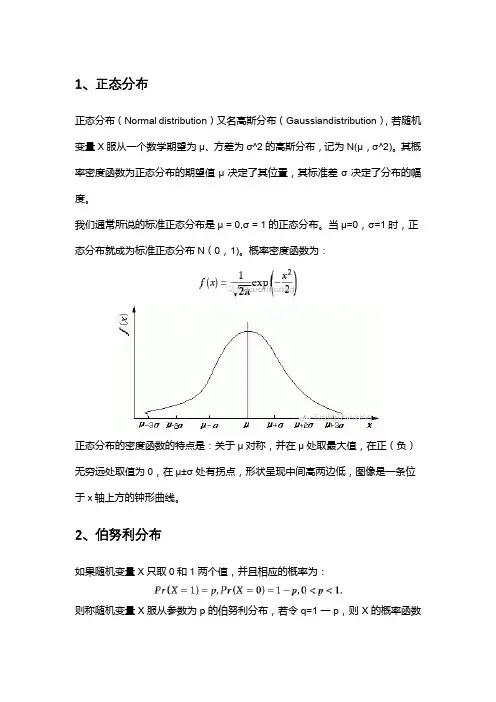
1、正态分布正态分布（Normal distribution）又名高斯分布（Gaussiandistribution），若随机变量X服从一个数学期望为μ、方差为σ^2的高斯分布，记为N(μ，σ^2)。

其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。

我们通常所说的标准正态分布是μ = 0,σ = 1的正态分布。

当μ=0，σ=1时，正态分布就成为标准正态分布N（0，1)。

概率密度函数为：正态分布的密度函数的特点是：关于μ对称，并在μ处取最大值，在正（负）无穷远处取值为0，在μ±σ处有拐点，形状呈现中间高两边低，图像是一条位于x轴上方的钟形曲线。

2、伯努利分布如果随机变量X只取0和1两个值，并且相应的概率为：则称随机变量X服从参数为p的伯努利分布，若令q=1一p，则X的概率函数可写为：伯努利分布（二点分布）的期望E(X)=p，D(X)=p(1-p)。

（其中，离散数据的方差计算公式为D(X)=E{[X-E(X)]^2}）n重伯努利分布（二项分布）的期望E(X)=np，D(X)=np(1-p)。

3、泊松分布在统计学上，只要某类事件满足三个条件，它就服从"泊松分布"。

三个条件分别是：①事件X的发生是小概率事件②事件X的发生是随机而且互相独立的③事件X发生的概率相对稳定。

泊松分布的公式为：各个参数的含义：单位时间(或单位面积)内随机事件的平均发生率，即P（X=k）事件X发生k次的概率，λ表示事件X稳定发生的概率。

当二项分布的n很大而p很小时，泊松分布可作为二项分布的近似。

设X~B（n,p)，当n很大,p很小,且λ＝np适中时,有P(x=k)≈λ^k/k! ·e^(-λ)，推导过程如下所示：为第二重要极限公式，上面的推到会涉及到。

正态分布的期望和方差公式推导设正态分布概率密度函数是f(x)=[1/(√2π)t]*e^[-(x-u)^2/2(t^2)]其实就是均值是u，方差是t^2于是：∫e^[-(x-u)^2/2(t^2)]dx=(√2π)t.（*）（1）求均值对（*）式两边对u求导：∫{e^[-(x-u)^2/2(t^2)]*[2(u-x)/2(t^2)]dx=0约去常数，再两边同乘以1/(√2π)t得：∫[1/(√2π)t]*e^[-(x-u)^2/2(t^2)]*(u-x)dx=0把(u-x)拆开，再移项：∫x*[1/(√2π)t]*e^[-(x-u)^2/2(t^2)]dx=u*∫[1/(√2π)t]*e^[-(x-u)^2/2(t^2)]dx也就是∫x*f(x)dx=u*1=u这样就正好凑出了均值的定义式，证明了均值就是u。

（2）方差对(*)式两边对t求导：∫[(x-u)^2/t^3]*e^[-(x-u)^2/2(t^2)]dx=√2π移项：∫[(x-u)^2]*[1/(√2π)t]*e^[-(x-u)^2/2(t^2)]dx=t^2也就是∫(x-u)^2*f(x)dx=t^2扩展资料：由于一般的正态总体其图像不一定关于y轴对称，对于任一正态总体，其取值小于x的概率。

只要会用它求正态总体在某个特定区间的概率即可。

为了便于描述和应用，常将正态变量作数据转换。

将一般正态分布转化成标准正态分布。

服从标准正态分布,通过查标准正态分布表就可以直接计算出原正态分布的概率值。

故该变换被称为标准化变换。

（标准正态分布表：标准正态分布表中列出了标准正态曲线下从-∞到X（当前值）范围内的面积比例。

）。

图 6-2 正态分布概率密度函数的曲线正态曲线可用方程式表示。

当n→∞时，可由二项分布概率函数方程推导出正态分布曲线的方程：f(x)= （6.16 ）式中： x —所研究的变数； f(x) —某一定值 x 出现的函数值，一般称为概率密度函数（由于间断性分布已转变成连续性分布，因而我们只能计算变量落在某一区间的概率，不能计算变量取某一值，即某一点时的概率，所以用“概率密度”一词以与概率相区分），相当于曲线 x 值的纵轴高度； p —常数，等于 3.14 159 ……； e —常数，等于 2.71828 ……；μ为总体参数，是所研究总体的平均数，不同的正态总体具有不同的μ ，但对某一定总体的μ 是一个常数；δ 也为总体参数，表示所研究总体的标准差，不同的正态总体具有不同的δ ，但对某一定总体的δ 是一个常数。

上述公式表示随机变数 x 的分布叫作正态分布，记作N( μ , δ2 ) ，读作“具平均数为μ，方差为δ2 的正态分布”。

正态分布概率密度函数的曲线叫正态曲线，形状见图 6-2 。

（二）正态分布的特性1 、正态分布曲线是以x= μ 为对称轴，向左右两侧作对称分布。

因的数值无论正负，只要其绝对值相等，代入公式（ 6.16 ）所得的 f(x) 是相等的，即在平均数μ 的左方或右方，只要距离相等，其 f(x) 就相等，因此其分布是对称的。

在正态分布下，算术平均数、中位数、众数三者合一位于μ点上。

2 、正态分布曲线有一个高峰。

随机变数 x 的取值范围为（ - ∞，+ ∞ ），在（ - ∞ ，μ ）正态曲线随 x 的增大而上升，；当 x= μ 时， f(x) 最大；在（μ ，+ ∞ ）曲线随 x 的增大而下降。

3 、正态曲线在︱x-μ︱=1 δ 处有拐点。

曲线向左右两侧伸展，当x →± ∞ 时，f(x) →0 ，但 f(x) 值恒不等于零，曲线是以 x 轴为渐进线，所以曲线全距从 -∞到+ ∞。

正态分布求导公式
本文讨论正态分布的求导公式，说明它的重要性及应用。

正态分布是统计学中最重要且广泛应用的分布模型之一。

它用于模拟一组变量的分布情况，并分析这些变量之间的关系。

正态分布的求导公式是：
$$f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}x^2}$$
正态分布的求导公式的重要性不言而喻。

它为统计学提供了一种有效的方法来分析各种类
型的随机变量彼此之间的关系。

此外，正态分布的求导公式还可用于确定数据所反映的分类。

正态分布的求导公式同样十分重要，它可以用来估计统计变量的期望并计算统计变量的方差。

在概率测试中，也可以利用该公式来进行条件测试，以确定自变量和因变量之间的关系。

此外，正态分布的求导公式还可以用于推断不确定的变量的分布情况，从而对潜在的趋势进行建模。

此外，它还可以用于模拟时间序列数据，通过构建基于正态分布的模型来预测未来的情况。

综上所述，正态分布的求导公式具有重要的意义，可以应用于统计学、概率测试、变量推测等多个领域，使之能够解决许多实际问题，对生活和研究都有益处。

正态分布函数公式是P(x)=(2π)^(-1/2)*σ^(-1)*exp{[-(x-μ)^2]/(2σ
^2)}。

其中F(y)为Y的分布函数，F(x)为X的分布函数。

其中μ为均数，σ为标准差。

μ决定了正态分布的位置，与μ越近，被取到的概率就越大，反之越小。

σ描述的是正态分布的离散程度，σ越大，数据分布越分散曲线越扁平。

σ越小，数据分布越集中曲线越陡峭。

若随机变量X服从一个位置参数为μ、尺度参数为σσ的概率分布，且其概率密度函数为f(x)=12π−−√σe−（x−μ）22σ2。

正态分布函数的特征
1、集中性，正态曲线的高峰位于正中央，即均数所在的位置。

2、对称性，正态曲线以均数为中心，左右对称，曲线两端永远不与横轴相交。

3、均匀变答动性，正态曲线由均数所在处开始，分别向左右两侧逐渐均匀下降。

4、正态分布有两个参数，即均数μ和标准差σ，可记作N（μ，σ）。

5、u变换，为了便于描述和应用，常将正态变量作数据转换。