下载文档原格式
第三节桥梁的支座一、概述1、支座作用传递上部结构的各种荷载适应温度、收缩徐变等因素产生的位移保证桥跨结构在墩台上的位置充分固定,不滑落2、支座布置桥梁支座的布置，应以有利于墩台传递纵向水平力，有利于梁体的自由变形为原则。
根据梁桥的结构体系以及桥宽，支座在纵、横桥向的布置方式主要有以下几种（1）简支梁桥应在每跨的一端设置固定支座，另一端设活动支座；对于多跨简支梁，一般把固定支座布置在桥台上，每个桥墩上布置一个（组）活动支座与一个（组）固定支座。
若个别墩较高，也可以在高墩上布两个（组）活动支座。
（2）对于坡桥，宜将固定支座布置在标高低的墩台上。
同时，为了避免整个桥跨下滑，影响车辆的行驶，当纵坡大于1%或横坡大于2%时，应使支座保持水平，通常在设置的梁底面，增设局部的楔形构造，如下图所示。
（3）对于桥面连续的简支梁及连续梁桥，一般在每一联设置一个固定支座，并宜将固定支座设置在靠近温度中心处以使全梁的纵向变形分散在梁的两端，其余墩台上均设置活动支座。
在设置固定支座的桥墩（台）上，一般采用一个固定支座，其余为横桥向的单向活动支座；在设置活动支座的所有桥墩（台）上，一般沿设置固定支座的一侧，均布置顺桥向的单向活动支座，其余均为双向活动支座。
对于一些特别宽的桥梁，尚应设置沿纵向和横向均能自由移动的活动支座。
铁路桥梁一般情况下桥面较窄，支座横向变位很小，一般只须设置单向活动支座(纵向活动支座)。
二、支座的类型和构造目前我国梁式桥使用的支座，按其容许变形的可能性可分为：(1)固定支座：它能承担支承点处顺桥向、横桥向的水平力和竖向反力，并约束相应的线位移。
(2)单向活动支座：它在承担竖向反力的同时，能约束顺桥向、横桥向水平位移中的一个线位移。
(3)多向活动支座：容许支座在顺桥向、横桥向两个方向发生水平线位移，仅承担竖向反力。
桥梁支座按使用材料来分，又可分为简易支座、钢支座、橡胶支座、混凝土支座等四大类。
应根据桥梁结构的跨径、支点反力的大小、梁体的变形程度等因素来选取支座类型。
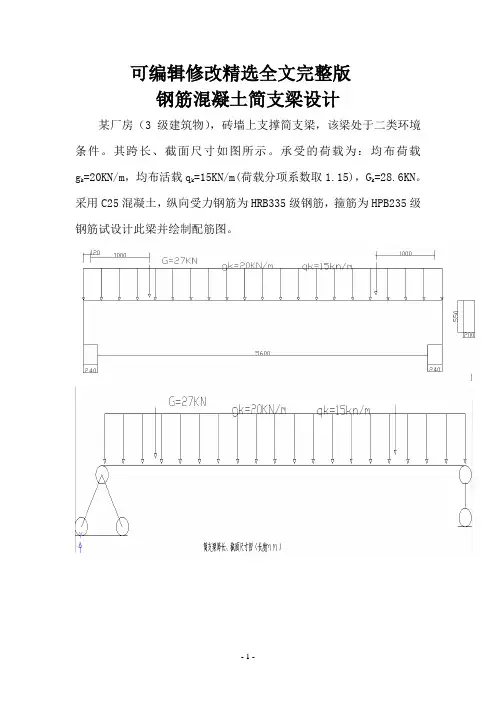
可编辑修改精选全文完整版钢筋混凝土简支梁设计某厂房（3级建筑物），砖墙上支撑简支梁，该梁处于二类环境条件。
其跨长、截面尺寸如图所示。
承受的荷载为：均布荷载g k=20KN/m，均布活载q k=15KN/m(荷载分项系数取1.15)，G k=28.6KN。
采用C25混凝土，纵向受力钢筋为HRB335级钢筋，箍筋为HPB235级钢筋试设计此梁并绘制配筋图。
钢筋混凝土简支梁设计一、基本资料（一）荷载分项系数1、永久荷载对结构有利r G=1.0，不利r G=1.22、可变荷载分项系数，一般情况下r Q=1.4,可控制r Q=1.15（二）材料强度设计值1、取G k=27KN,C25混凝土ƒc=11.9MPa, ƒt=1.27 MPa.2、钢筋级别为：纵向受力钢筋HRB335 ƒy= ƒy、=310 MPa，箍筋及其他纵向构造钢筋HPB235 ƒy=210 MPa.3、混凝土保护层厚度（环境类别二类环境）c=35㎜；最小配筋率ρmin=0.2%二、截面几何尺寸拟定（一）梁的截面高度h根据相应结构和设计经验与并考虑构造要求及施工方面等因素，按不需要作挠度验算的最小截面高度h，计算梁的高度.取表中独立梁：h=1/12×l0=1/12×5.84=487㎜；取h=550 （二）当梁的高度确定以后、梁的截面宽度可由常用的高宽比估计计算：矩形截面梁b=（1/2-1/3）h=（1/2-1/3）×550=183.3～275㎜，当量的宽度、高度计算完成后按建筑模数取整数；取b=200㎜,故截面几何尺寸为b×h=200×550㎜，如下图所示（三）计算跨度l0（式中a为支撑长度）l n=l-a=5840-240=5600㎜由l0=1.025 l n=5600×1.025=5740㎜l0= l n+a=5600+240=5840㎜取两者较小值；得l0=5740㎜（四）计算简图三、荷载计算钢筋混凝土容重r钢筋砼=25KN/㎡；水泥砂浆容重r砂浆=17 KN/㎡1、梁的自重计算标准值（包括侧梁、底15㎜抹灰重）g k=0.2×0.55×25+17×0.015×0.55×2+17×0.015×0.2=3.08KN/m22、荷载计算对于基本组合，荷载效应组合的设计值S应从下列组合中取最不利值（1）由可变荷载控制集中力：S F=r G G k=1.2×27=32.4KN均布荷载：S g= r G G k +r Q q k=1.2×3.08+1.4×15=24.70KN (2) 可永久荷载控制集中力：S F=r G G k=1.0×27=27KN均布荷载：S g= r G G k +r Q q k=1.0×20+1.15×15=37.25KN两者取较大集中值：S F=32.4KN均布荷载：S g=37.25KN四、内力计算内力图绘制(一)支座反力计算该结构为对承结构；根据材料力学理论可知，对承结构在对称荷载作用下，其支座反力为：R A=R B=S F+1/2×S g l0=32.4+1/2×37.25×5.74=139.31KN(二)设计值计算(式中a为集中力至支座边缘的距离)由材料力学理论得知，对称结构在对称荷载作用下采用叠加法得结构跨中控制截面弯矩设计值为：M max=S F a’+1/8S g l02=32.4×0.48+1/8×37.25×5.742=168.96KN/m（三）支座边缘截面的最大剪力设计值计算(a为支座的支撑长度)因：VＡ =VＢ=ＲＡ=139.31KN故：VＡ右=VＢ左=ＲＡ-1/2S g a=139.31-1/2×37.25×0.24=134.84KN（四）集中力（G+Q）处的剪力设计值计算(a为集中力至支座边缘的距离)V c右=ＲＡ- 1/2（g+q）a=139.31- 1/2×37.25×0.48=130.37KNV c左=ＲＡ- 1/2（g+q）a-(Q+G)=139.31- 1/2×37.25-25×0.48-32.4=97.97KN简支梁内力汇总表（五）弯矩与剪力图绘制五、截面几何尺寸复核因弯矩设计值较大设钢筋排二排：a s=c+d+e/2=35+10+25/2=57.5㎜,故a=60㎜;则截面有效高度h0=h-a=550-60=490㎜；因为是矩形截面好h0=h w；则h w/b=490/200=2.45﹤4；由0.25ƒc bh0=0.25×11.9×200×490=291.55KN﹥VＡ右；说明截面积和尺寸符合要求。
钢筋混凝土简支梁试验实验报告一、实验目的本次实验的目的是通过对钢筋混凝土简支梁的试验, 掌握梁的受力性能, 了解梁的破坏形态和破坏机理, 以及掌握梁的设计方法。
二、实验原理钢筋混凝土简支梁是一种常见的结构形式, 其受力性能主要由梁的几何形状、材料性质和荷载大小等因素决定。
在实验中, 我们主要关注以下几个方面:1.梁的受力状态在荷载作用下, 梁会发生弯曲变形, 产生弯矩和剪力。
弯矩和剪力的大小和分布情况决定了梁的受力状态。
2.梁的破坏形态当荷载达到一定大小时, 梁会发生破坏。
破坏形态主要有弯曲破坏、剪切破坏和挤压破坏等。
3.梁的设计方法根据梁的受力状态和破坏形态, 可以采用不同的设计方法来确定梁的尺寸和钢筋配筋。
三、实验装置和材料本次实验采用的是静载试验法, 实验装置包括试验机、测力传感器、位移传感器和数据采集系统等。
试验材料为混凝土和钢筋, 混凝土强度等级为C30, 钢筋型号为HRB400。
四、实验步骤1.制作试件根据设计要求, 制作出符合要求的钢筋混凝土简支梁试件。
2.安装试件将试件安装在试验机上, 并调整试验机的荷载和位移控制系统。
3.施加荷载逐渐施加荷载, 记录荷载和位移数据, 并观察试件的变形情况。
4.记录数据在试验过程中, 需要记录荷载、位移、应变等数据, 并及时进行处理和分析。
5.分析结果根据试验数据, 分析梁的受力状态、破坏形态和破坏机理, 并进行设计计算。
五、实验结果本次实验的试件尺寸为200mm×300mm×2000mm, 荷载施加方式为集中荷载。
试验结果如下:1.荷载-位移曲线试验中记录了荷载-位移曲线, 如图1所示。
从图中可以看出, 在荷载逐渐增加的过程中, 试件的位移也逐渐增加, 直到试件发生破坏。
2.破坏形态试件的破坏形态如图2所示。
从图中可以看出, 试件发生了弯曲破坏, 破坏位置在距离支座较远的位置。
3.破坏机理试件的破坏机理主要是由于弯矩作用下, 混凝土受到拉应力和钢筋受到压应力, 导致混凝土的开裂和钢筋的屈服和断裂。
