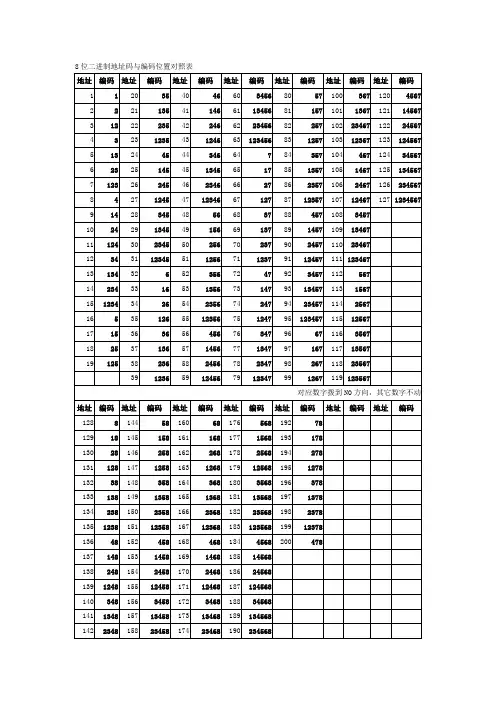
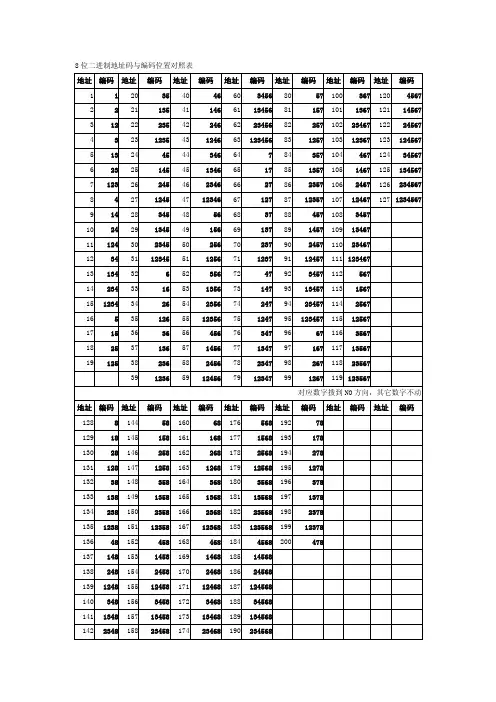
8位二进制地址码与编码位置对照表

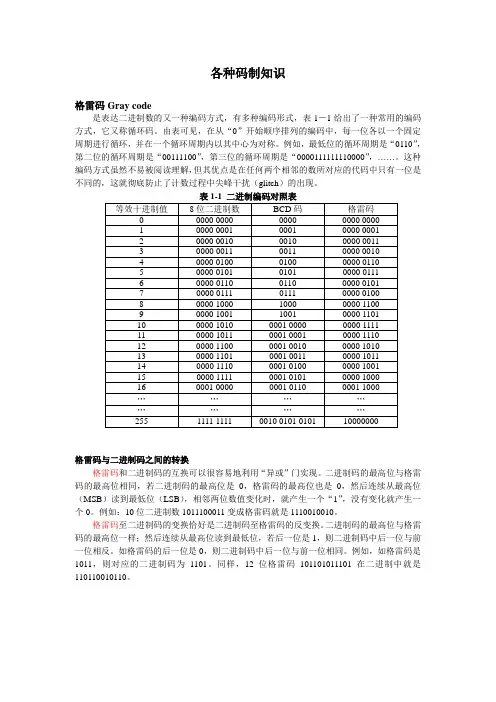
各种码制知识格雷码Gray code是表达二进制数的又一种编码方式，有多种编码形式，表1－1给出了一种常用的编码方式，它又称循环码。

由表可见，在从“0”开始顺序排列的编码中，每一位各以一个固定周期进行循环，并在一个循环周期内以其中心为对称。

例如，最低位的循环周期是“0110”，第二位的循环周期是“00111100”，第三位的循环周期是“0000111111110000”，……。

这种编码方式虽然不易被阅读理解，但其优点是在任何两个相邻的数所对应的代码中只有一位是不同的，这就彻底防止了计数过程中尖峰干扰（glitch）的出现。

格雷码与二进制码之间的转换格雷码和二进制码的互换可以很容易地利用“异或”门实现。

二进制码的最高位与格雷码的最高位相同，若二进制码的最高位是0，格雷码的最高位也是0，然后连续从最高位（MSB）读到最低位（LSB），相邻两位数值变化时，就产生一个“1”，没有变化就产生一个0。

例如：10位二进制数1011100011变成格雷码就是1110010010。

格雷码至二进制码的变换恰好是二进制码至格雷码的反变换。

二进制码的最高位与格雷码的最高位一样；然后连续从最高位读到最低位，若后一位是1，则二进制码中后一位与前一位相反。

如格雷码的后一位是0，则二进制码中后一位与前一位相同。

例如，如格雷码是1011，则对应的二进制码为1101。

同样，12位格雷码101101011101在二进制中就是110110010110。

111二进制格雷码111二进制格雷码常用双极性代码符号位不变，其余取反对负数：加一无论正负数，最高位取反各种双极性代码的相互关系。

标准ascii用8位二进制对128种符号进行编码ASCII是一种基于8位二进制编码的字符集，其中包含128种不同的字符。

ASCII的全称是美国信息交换标准代码（American Standard Code for Information Interchange），它在20世纪60年代被制定出来，并成为了标准化的字符编码方式。

在计算机科学的发展史上，ASCII扮演了非常重要的角色，它为后来的编码方式奠定了基础。

在ASCII编码中，每一个字符都对应着一个唯一的8位二进制数字，也就是8个0或1组成的序列。

因为8个二进制数字总共有256种不同的组合方式，而ASCII只使用了其中的128种组合。

其中包括数字、字母、标点符号和一些控制字符等等。

让我们来看一下具体的ASCII编码规则。

1. 数字：ASCII编码中包含了0-9的十个数字，分别对应了0x30-0x39这十个16进制数字。

例如，字符“1”的ASCII码为0x31，字符“9”的ASCII码为0x39。

2. 字母：ASCII编码中包含了大小写26个英文字母，分别从0x41-0x5A为大写字母A到Z，0x61-0x7A为小写字母a到z。

例如，字符“A”的ASCII码为0x41，字符“a”的ASCII码为0x61。

3. 标点符号：ASCII编码中包含了常用的标点符号，例如句号、逗号、感叹号、分号等等，这些字符分别对应了0x20-0x2F和0x3A-0x3F这两个区间。

例如，字符“！”的ASCII码为0x21，字符“.”的ASCII码为0x2E。

4. 控制字符：ASCII编码中还包含了一些不可打印的控制字符，这些字符用于控制计算机的硬件以及通信协议等方面。

例如，回车键的ASCII码为0x0D，换行键的ASCII码为0x0A，空格键的ASCII码为0x20。

总的来说，ASCII编码是一种非常基础的字符编码方式，它使用8位二进制数来对128种字符进行编码，广泛应用于计算机科学的各个领域。

8 位二进制数(1 位符号位,7 位数值位),其原码所能表示的十进制数范围解释说明1. 引言1.1 概述本文将介绍8位二进制数的表示方法及其所能表示的十进制数范围。

二进制数是计算机系统中最基本的数字表示方式之一，它由0和1两个数字组成，并且能够通过不同的编码方式来表示正负数。

了解二进制数的表示方法对于理解计算机内部运算和数据储存有着重要意义。

1.2 文章结构文章将按照以下结构进行介绍：首先，我们会从二进制数的概念入手，解释什么是二进制数以及它如何在计算机中表示。

随后，我们会详细讨论8位二进制数的结构和表示范围，分别涵盖正数和负数。

接着，我们会给出从十进制到八位二进制数以及从八位二进制数到十进制的转换示例。

最后，我们会总结文章内容，并探讨原码在计算机中应用场景和限制。

1.3 目的本文旨在提供读者关于8位二进制数和其原码表示法所能表示的十进制范围的全面理解。

通过阅读本文，读者将了解到不同编码方式对于数字范围和精度带来的影响，并且可以更好地理解计算机内部的数值运算和数据表示。

对于学习计算机科学和数字电路等领域的读者来说，本文将为他们打下坚实的基础。

2. 二进制数的表示方法2.1 二进制数的概念二进制数是一种数字系统，只包含两个数字，0和1。

在计算机中，信息以二进制形式存储和处理。

2.2 二进制数的符号位和数值位在一个n 位的二进制数中，第一位为符号位（最高位），用来表示正负。

剩余的n-1 位为数值位，用来表示具体的值。

2.3 原码表示法原码表示法是一种最简单直观的表示方式，即用二进制表示一个数，将符号位与数值位组合起来。

其中最高位为符号位（0代表正数，1代表负数），其余各个位置代表对应的权重。

例如，在8位二进制中，00011001 表示十进制数+25, 而10011001 则表示-25。

原码表示法的优点是简单易理解，在加法运算时也比较简单、直观。

但是也存在一些缺点。

首先，任何一个非零整数都有两个零对应：+0 和-0 ，造成了冗余；其次，在进行减法时需要自行判断两个操作数之间大小关系，并注意借位的处理。

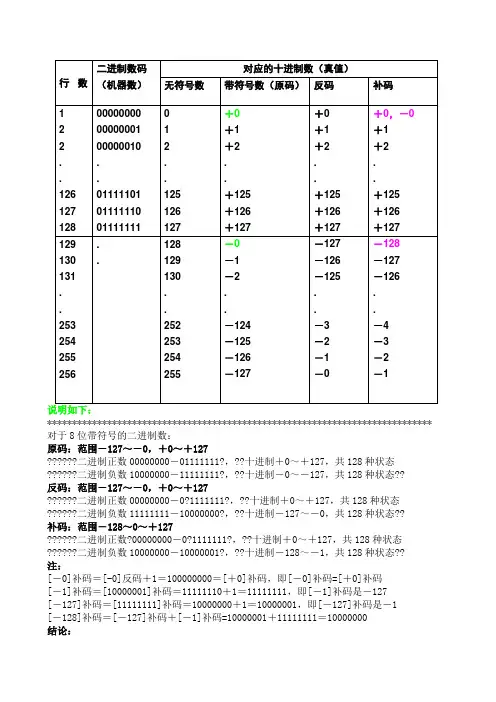
***************************************************************************** 对于8位带符号的二进制数：原码：范围－127～－0，＋0～＋127??????二进制正数00000000－01111111?，??十进制＋0～＋127，共128种状态??????二进制负数10000000－11111111?，??十进制－0～－127，共128种状态??反码：范围－127～－0，＋0～＋127??????二进制正数00000000－0?1111111?，??十进制＋0～＋127，共128种状态??????二进制负数11111111－10000000?，??十进制－127～－0，共128种状态??补码：范围－128～0～＋127??????二进制正数?00000000－0?1111111?，??十进制＋0～＋127，共128种状态??????二进制负数10000000－10000001?，??十进制－128～－1，共128种状态??注：[－0]补码＝[-0]反码＋1＝100000000＝[＋0]补码，即[－0]补码=[＋0]补码[－1]补码＝[10000001]补码＝11111110＋1＝11111111，即[－1]补码是－127[－127]补码＝[11111111]补码＝10000000＋1＝10000001，即[－127]补码是－1[－128]补码＝[－127]补码＋[－1]补码=10000001＋11111111＝10000000结论：原码范围：－127～－0，＋0～＋127，256种状态反码范围：－127～－0，＋0～＋127，256种状态补码范围：－128～－1，＋0～＋127，256种状态，因为[－0]补码和[＋0]补码相同，在补码中－128代替了－0。

也可认为是一种规定，这样可都是256种状态。

要注意：(-128)没有相对应的原码和反码,(-128)=*****************************************************************************。

二、八、十、十六进制对照表进制转换是计算机科学中的一个重要课题，并且在数字逻辑和计算中发挥着重要作用。

在一种进制转换成另一种进制时，我们常常需要借助“进制表”来辅助计算。

在本文中，我们将对比分析二进制、八进制、十进制和十六进制之间的关系，并用表格的形式来展现它们的对照表。

下面就来一起认识一下吧！首先，让我们来了解一下什么是进制。

所谓进制，就是指一个计数系统里使用的基数或底数。

当我们把一个数表示成几个数之和的形式时，每一个数就叫做一个进制。

常见的进制有二进制、八进制、十进制和十六进制，分别使用0，1，2，3，4，5，6，7，8，9，A，B，C，D，E，F这15个数来表示。

其次，让我们看一下它们之间的转换。

要从十进制转换成其它进制，我们可以采用除法取余法，先除以2，然后除以8，再除以16，我们就可以得到每一位的余数，然后以进制表中对应的数字来表示。

同样的，我们可以用乘法取商法来从其它进制转换成十进制，先把每一位的数字乘以2，8，16，再把它们相加，就可以得到转换的结果。

最后，让我们来看看它们之间的对照表：二进制|八进制|十进制|十六进制------|------|------|------0|0|0|01|1|1|110|2|2|211|3|3|3100|4|4|4101|5|5|5110|6|6|6111|7|7|71000|10|8|81001|11|9|91010|12|10|A1011|13|11|B1100|14|12|C1101|15|13|D1110|16|14|E1111|17|15|F从上面的表格中，我们可以发现它们之间的关系，当我们从十进制转换成其它进制时，我们只需要从左到右逐位除以进制的底数，然后取余数；当我们从其它进制转换成十进制时，我们只需要从右到左把每一位乘以底数的幂，然后把它们相加即可。

以上就是二、八、十、十六进制之间的对照表，希望本文能够帮助大家熟悉这几种有关进制转换的知识。

二进制8位移码
二进制8位移码是一种用于表示数字的编码方式，其字长为8位。

在这种编码方式中，每个数字都可以表示为一个8位的二进制数。

在IEEE 754标准中，移码被定义为阶码，但其偏置值和普通的移码不同。

以单精度浮点数为例（32位），其中的阶码的位数为8，偏置值为127，即二进制数01111111，因此在转换时需要加减这个偏置值。

而普通的8位移码的偏置值为128，即二进制数10000000，因此在由补码转化成移码时，只需要将最高位（即符号位）取反即可，亦即相当于加减偏置值。

移码在计算机科学和数字通信领域中被广泛应用，它能够有效地表示和处理二进制数字。

8位二进制原码范围1. 什么是二进制原码？在计算机科学中，二进制原码是一种用于表示数值的编码方式。

它将一个数值分成了整数部分和小数部分，每一部分由一串二进制数字组成。

在8位二进制原码中，一共可表示256个不同的整数。

2. 8位二进制原码的表示范围8位二进制原码的表示范围从00000000到11111111，对应于十进制的0到255。

这个范围内的整数可以通过这8位的二进制数来表示和计算。

3. 为什么使用8位二进制原码？在计算机系统中，二进制是最基本的数据表示方式。

通过使用8位二进制原码，可以用较少的位数存储和传输大部分常用的整数数值。

这样可以节省存储空间和提高计算效率。

4. 8位二进制原码的优点和局限性4.1 优点•简洁：使用8位二进制原码可以用较少的位数表示整数，减少了计算机系统中的存储和传输压力。

•高效：计算机对于二进制的处理速度更快，使用8位二进制原码可以加快计算速度。

•兼容性：8位二进制原码可以与其他计算机系统的表示方式进行转换和兼容。

4.2 局限性•表示范围：8位二进制原码只能表示0到255的整数，对于超过这个范围的数值无法准确表示。

•符号位：8位二进制原码中的最高位可以表示符号，即正(0)和负(1)。

然而，由于只有一位来表示符号，所以只能表示有限的正负数值。

5. 8位二进制原码的应用场景8位二进制原码广泛应用于计算机科学和信息技术领域。

以下是一些常见的应用场景：5.1 数值计算在数值计算中，使用8位二进制原码可以有效地进行整数运算。

它能够提供高效的加减乘除运算，并且可以与其他数据类型进行转换。

5.2 存储空间在存储空间有限的场景下，使用8位二进制原码可以有效地节省存储空间。

例如，在嵌入式系统中，通常会使用较小的存储单元来保存数据。

5.3 网络传输在网络传输中，数据需要被转换为二进制格式进行传输。

使用8位二进制原码可以减少数据的大小，提高传输效率。

6. 如何将十进制数转换为8位二进制原码？将十进制数转换为8位二进制原码可以按照以下步骤进行：1.判断数值的符号，正数为0，负数为1。

八位二进制数原码范围在计算机科学中，二进制数是一种基于2的数制系统，它由0和1两个数字组成。

八位二进制数是指由8个二进制位（0或1）组成的数字。

在二进制数中，每位的权值是2的幂次方，从右往左依次增加。

在八位二进制数中，最大的数是11111111，转换为十进制是255；最小的数是00000000，转换为十进制是0。

因此，八位二进制数的原码范围是从0到255。

原码是一种用于表示有符号整数的编码方式。

在八位二进制数中，最高位用作符号位，0表示正数，1表示负数。

因此，在八位二进制数中，有符号整数的范围是从-128到127。

当八位二进制数的符号位为0时，表示的是正数。

例如，01010101表示85，10101010表示170。

这些数可以用来表示很多物理量，比如温度、速度等。

当八位二进制数的符号位为1时，表示的是负数。

例如，11000000表示-64，10000001表示-127。

负数的表示方式有很多种，常见的有补码和反码。

补码是一种常用的表示负数的方式。

在八位二进制数中，负数的补码是其原码按位取反后再加1。

例如，-1的原码是10000001，其补码是11111111；-2的原码是10000010，其补码是11111110。

原码和补码的转换是通过对原码进行取反再加1来实现的。

例如，将11111111转换为原码，先将其取反得到00000000，然后加1得到00000001，即为1的原码。

在八位二进制数中，原码和补码的转换可以通过逐位取反再加1来实现。

例如，将10000001转换为补码，先将其逐位取反得到01111110，然后加1得到01111111，即为-127的补码。

在八位二进制数中，原码和补码的范围是相同的，都是从-128到127。

因此，八位二进制数的原码范围也可以看作是补码范围。

除了原码和补码，还有一种表示负数的方式是反码。

在八位二进制数中，负数的反码是其原码按位取反。

例如，-1的原码是10000001，其反码是11111110；-2的原码是10000010，其反码是11111101。